基于二進制序列族的壓縮感知測量矩陣構造

蘆存博 肖 嵩 權 磊

?

基于二進制序列族的壓縮感知測量矩陣構造

蘆存博*肖 嵩 權 磊

(西安電子科技大學ISN國家重點實驗室 西安 710071)

構造確定性測量矩陣對壓縮感知理論的推廣與應用具有重要的意義。該文源于代數編碼理論，提出一種基于二進制序列族的確定性測量矩陣構造算法。相關性是描述矩陣性質的重要準則，減小相關性可使重建性能提高。該文推導出所構造測量矩陣的相關性小于同條件下的高斯隨機矩陣和伯努利隨機矩陣。理論分析和仿真實驗表明，該方式構造的測量矩陣的重建性能優于同條件下的高斯隨機矩陣和伯努利隨機矩陣；所構造矩陣可由線性反饋移位寄存器結構實現，易于硬件實現，有利于壓縮感知理論的實用化。

信號處理；壓縮感知；測量矩陣；二進制序列族

1 引言

壓縮感知(Compressed Sensing, CS)[1,2]的概念是2006年Donono和Candes等人提出的，它是一種不同于奈奎斯特(Nyquist)采樣定律的全新信號采樣框架。CS可實現以遠低于Nyquist的采樣率去采樣稀疏信號，其核心是利用測量矩陣將高維稀疏信號投影到一個低維空間上，然后利用信號的稀疏性，通過重建算法以高概率實現原始信號的精確重建。這種提高采樣效率的新思路引起了學術界的廣泛關注，CS在數字信號處理、信息論、通信、光學成像、雷達等領域受到高度關注。

CS過程分為兩部分：數據采樣和信號重建，在這兩部分中測量矩陣都起著至關重要作用。首先，在數據采樣中，好的測量矩陣可以以較少的測量數目達到相同的重構精度。其次，在信號重建中，在相同的采樣率下得到的數據，好的測量矩陣對信號可以達到較高的重構精度。總體來說，好的測量矩陣能夠在投影測量時保持原始信號的全部信息，并可結合測量值重構出原始信號。測量矩陣的性質決定了能否將原始信號的全局信息保存下來。文獻[3]提出了測量矩陣必須滿足的性質-約束等距性(Restricted Isometry Property, RIP), 即只要測量矩陣滿足RIP特性，那么就能以高概率從低維的測量結果向量中準確地恢復出原信號。相關性(coherence)是建立矩陣RIP的另一個重要方法，文獻[4]指出了相關性跟RIP的關系：低相關性的矩陣滿足RIP。矩陣的RIP[5,6]和相關性均是分析測量矩陣性質的重要工具，本文將采用相關性對所構造測量矩陣的性質進行分析和說明。

測量矩陣可以分為隨機測量矩陣和確定性測量矩陣。在隨機矩陣中比較常用的是高斯矩陣和伯努利矩陣。由于隨機矩陣能夠以很大概率滿足RIP, 因此在科研上被廣泛應用。但是在隨機矩陣中，每一個元素都是獨立同分布的，存在不確定性，使得每一個元素都要存儲，耗費大量的存儲資源，并且隨機數的產生對硬件要求很高，不利于硬件實現，使得其實際應用受限。確定性測量矩陣的元素和值都是確定的，可以克服這些不足。許多研究者利用一些技術來構造確定性測量矩陣。例如，文獻[7]指出好的原模圖低密度奇偶校驗碼(Low Density Parity Check, LDPC)校驗矩陣可以作為測量矩陣；文獻[8]采用m序列構造出性能較好的測量矩陣；文獻[9]利用Berlekamp-Justesen碼構造測量矩陣；文獻[10]采用范德蒙矩陣構造出性能較好的測量矩陣；文獻[11]用混沌序列構造測量矩陣；文獻[13]用Reed- Solomon碼構造測量矩陣等。

本文將在文獻[14]中二進制序列族(Binary Sequence Family, BSF)的基礎上構造一種確定性測量矩陣(Binary Sequence Family based Deterministic Measurement Matrix, BSFDMM)，它是一種由+1和-1組成的雙極性矩陣，并推導出了矩陣BSFDMM的相關性小于同條件下的高斯隨機矩陣和伯努利隨機矩陣。理論分析和仿真實驗表明，文中矩陣BSFDMM的重建性能優于同條件下的高斯隨機矩陣和伯努利隨機矩陣。

2 基本理論

2.1 壓縮感知

上述求解問題是NP-hard。CS理論證明了在適當的測量矩陣下，該問題可以轉化為求解最小1范數優化問題，即

該問題可以通過基追蹤(Basis Pursuit, BP)算法[15]，得到與式(1)等價的最稀疏估計。目前，有一些直接求解式(1)的貪婪追蹤類算法，該類算法通過迭代求解局部最優解，最終逼近全局最優，從而得到原始信號的精確估計。例如，正交匹配追蹤(Orthogonal Matching Pursuit, OMP)[16]。

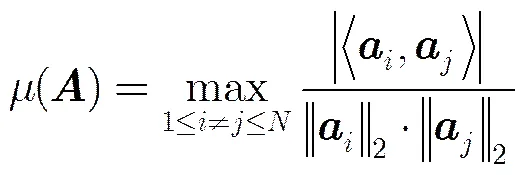
2.2 跡函數

3 測量矩陣構造

本文矩陣BSFDMM的具體實現步驟如下：

一旦給定數值轉換函數式(5)和有限域上的跡表示函數式(3)或式(4)，則能確定出所構造矩陣的每一個元素值，避免了隨機矩陣的不確定性；BSFDMM矩陣的元素結構使其非常便于硬件實現，數值轉換函數式(5)的本質是元素替換，在硬件實現上只用改變相應元素的輸出即可，非常簡單；又因為矩陣BSFDMM的生成過程中，使用的是文獻[14]的跡表示函數，從文獻[14]可得，BSFDMM矩陣可由LFSR結構實現，易于硬件實現，有利于壓縮感知理論的實用化。

4 相關性分析

相關性是描述矩陣性質的重要準則，減小相關性可使重建性能提高。本節給出所構造矩陣BSFDMM的相關性大小的上界，并推導出矩陣BSFDMM的相關性小于同條件下的高斯隨機矩陣和伯努利隨機矩陣，進而可從理論上證明矩陣BSFDMM的重建性能優于同條件下的高斯隨機矩陣和伯努利隨機矩陣。

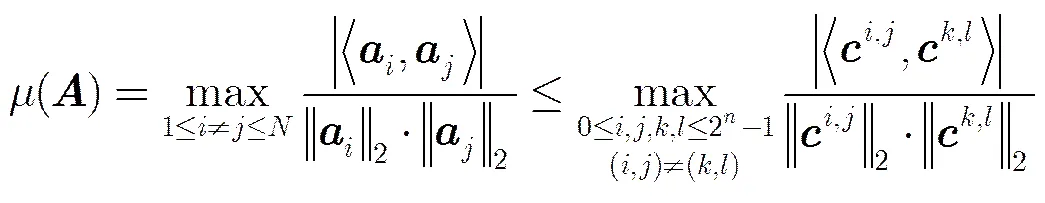
為了比較本文中的BSFDMM和同條件下的高斯隨機矩陣和伯努利隨機矩陣的重建性能，可以比較它們的相關性大小。首先引入以下文獻[18]的兩個引理：

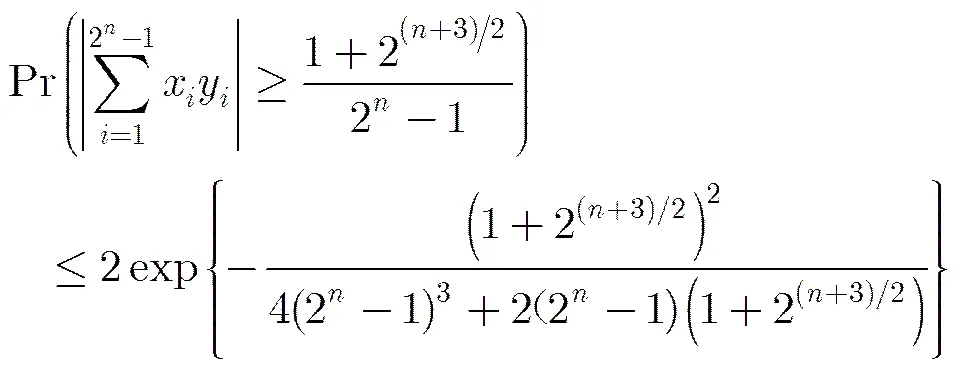
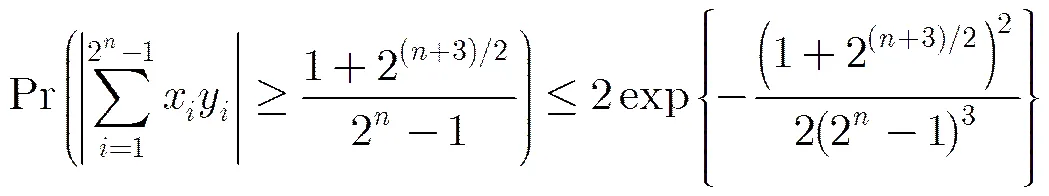
減小相關性能使可重建信號的稀疏度增大，重建性能提高。由定理1和定理2可以得到以下結論：

結論2 矩陣BSFDMM的重建性能優于同條件下的高斯隨機矩陣。

結論3 矩陣BSFDMM的重建性能優于同條件下的伯努利隨機矩陣。

5 實驗仿真及分析

比較了本文矩陣BSFDMM與相同大小的高斯隨機測量矩陣Gauss和伯努利隨機測量矩陣Bernoulli在無噪聲條件和有噪聲條件下的重建性能，其中矩陣BSFDMM分為兩種情況：(1)對應于是偶數的情況，此時矩陣大小為；(2)對應于是奇數的情況，此時矩陣大小為。通過隨機選取支撐位置，且支撐值服從標準的高斯分布，來生成被采樣的稀疏信號，其長度為。對每個稀疏度，用MATLAB生成1000次，重構算法選取OMP算法，若重建結果滿足，則重建實驗成功，重建概率即為精確重建次數與總次數的比值。Gauss矩陣的每一個元素取值服從獨立同分布的標準正態分布。Bernoulli矩陣的每一個元素取值服從獨立同分布的貝努利分布，且元素由+1和-1組成。

5.1無噪聲重建

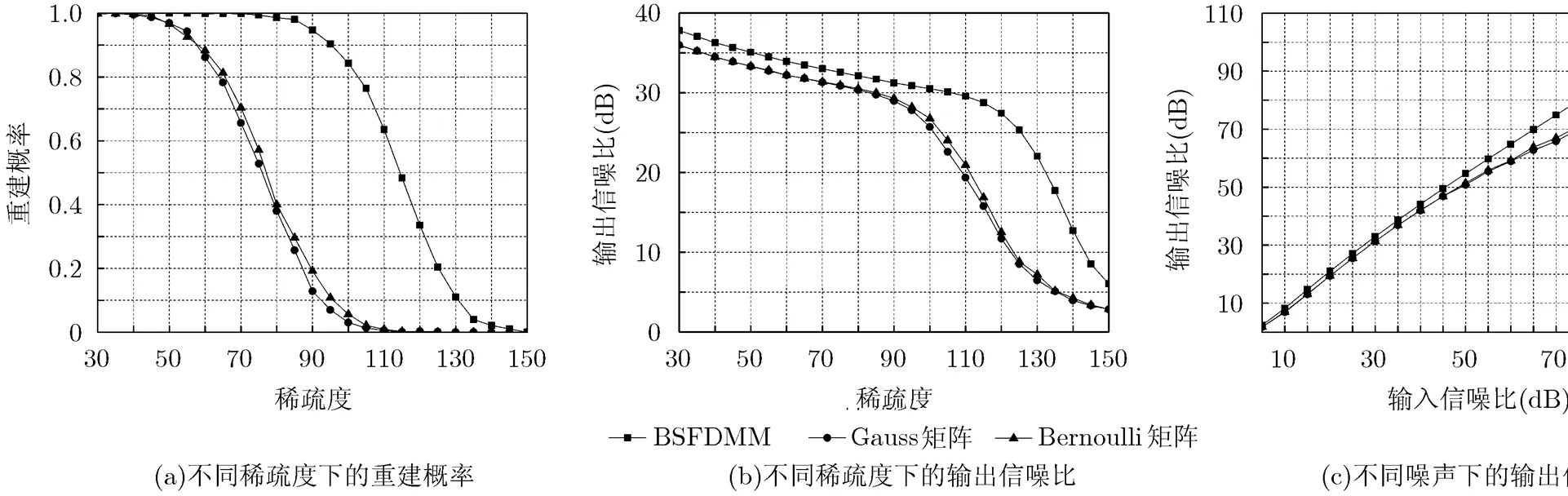
圖1 BSFDMM大小為255512的情況

由圖1(a)的重建曲線可以看出，對于矩陣BSFDMM，當信號稀疏度達到60時，才開始出現重建失敗的情況。然而，相同大小的Gauss矩陣和Bernoulli矩陣在稀疏度分別為35和30時，就已經開始出現重建失敗的情況。當信號稀疏度分別增大到130和125時，Gauss矩陣和Bernoulli矩陣就完全不能重建出原始信號。而矩陣BSFDMM在信號稀疏度增大到145時，依然有重建的可能。

從圖2(a)的重建曲線可以看出，對于矩陣BSFDMM，當信號稀疏度達到30時，才開始出現重建失敗的情況。然而，相同大小的Gauss矩陣和Bernoulli矩陣在稀疏度都為15時，就已經開始出現重建失敗的情況。當信號稀疏度增大到70時，Gauss矩陣和Bernoulli矩陣兩者都完全不能重建出原始信號。而矩陣BSFDMM在信號稀疏度增大到80時，依然有重建的可能。

從圖1(a)和圖2(a)的邊界條件分析可見，矩陣BSFDMM的信號恢復效果比相同大小的Gauss矩陣和Bernoulli矩陣效果好，這是因為矩陣BSFDMM的相關性小于相同大小的Gauss矩陣和Bernoulli矩陣，可重建信號的稀疏度增大，重建性能提高。

5.2有噪聲重建

圖2 BSFDMM大小為127256的情況

從圖1(b)和圖2(b)可以看出，矩陣BSFDMM的信號恢復效果比相同大小的Gauss矩陣和Bernoulli矩陣效果好，這是因為矩陣BSFDMM的相關性小于后兩者，更有利于信號重構。

從圖1(c)和圖2(c)可知，在不同輸入噪聲條件下，采用本文所構造的BSFDMM矩陣，進行重建后的輸出信噪比比采用高斯隨機測量矩陣和伯努利隨機測量矩陣的都要高。隨著輸入信噪比的增加，3種矩陣的輸出信噪比都隨之增加。在圖1(c)中，當輸入信噪比小于40 dB時，由于噪聲的影響，3種矩陣的輸出信噪比曲線整體區分并不是非常明顯，而從輸入信噪比大于40 dB開始，3種矩陣的輸出信噪比曲線區分開始明顯，此時BSFDMM矩陣相關性小的優勢開始明顯體現。隨著輸入信噪比的增加，BSFDMM矩陣的輸出信噪比曲線與其它兩種矩陣的曲線的區分越來越明顯。從圖2(c)中也可以得到3種矩陣輸出信噪比曲線類似的規律。

通過上述仿真發現，BSFDMM矩陣比相同條件下的高斯隨機矩陣和伯努利隨機矩陣的抗噪聲性能都要好，說明本文矩陣不僅在無噪聲條件下表現良好，在噪聲環境中同樣具有良好的重建性能，即表明文中所提矩陣的實用性。

6 結論

在二進制序列族的基礎上，本文構造了一種確定性測量矩陣- BSFDMM，它是一種由+1和-1組成的雙極性矩陣，并通過理論推導，得到所構造矩陣的相關性小于同條件下的高斯隨機矩陣和伯努利隨機矩陣。理論分析和仿真實驗表明，在相同條件下，BSFDMM矩陣不僅在無噪聲條件下的重建性能優于高斯隨機矩陣和伯努利隨機矩陣，而且在噪聲環境下其抗噪聲性能也比高斯矩陣和伯努利矩陣要好，說明了文中矩陣的實用性。矩陣BSFDMM可由LFSR結構實現，易于硬件實現，有利于壓縮感知理論的實用化。

[1] CANDES E J, ROMBERG J, and TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509. doi: 10.1109/TIT.2005.862083.

[2] DONOHO D L. Compressed sensing[J]., 2006, 52(4): 1289-1306. doi: 10.1109 /TIT.2006.871582.

[3] CANDES E J and TAO T. Decoding by linear programming [J]., 2005, 51(12): 4203-4215. doi: 10.1109/TIT.2005.858979.

[4] BOURGAIN J, DILWORTH S, FORD K,. Explicit constructions of RIP matrices and related problems[J]., 2011, 159(1): 145-185. doi: 10.1215/ 00127094-1384809.

[5] GAN H, LI Z, LI J,. Compressive sensing using chaotic sequence based on chebyshev map[J]., 2014, 78(4): 2429-2438. doi: 10.1007/s11071-014-1600-1.

[6] CASTORENA J and CREUSERE C D. The restricted isometry property for banded random matrices[J]., 2014, 62(19): 5073-5084. doi: 10.1109/TSP.2014.2345350.

[7] ZHANG J, HAN G, and FANG Y. Deterministic construction of compressed sensing matrices from protograph LDPC codes[J]., 2015, 22(11): 1960-1964. doi: 10.1109/LSP.2015.2447934.

[8] 黨骙, 馬林華, 田雨, 等. m序列壓縮感知測量矩陣構造[J].西安電子科技大學學報, 2015, 42(2): 186-192. doi: 10.3969/ j.issn.1001-2400.2015.02.031.

DANG Kui, MA Linhua, TIAN Yu,. Construction of the compressive sensing measurement matrix based on m sequences[J]., 2015, 42(2): 186-192. doi: 10.3969/j.issn.1001-2400.2015.02.031.

[9] 夏樹濤, 劉璐, 劉鑫吉. 基于Berlekamp-Justesen碼的壓縮感知確定性測量矩陣的構造[J]. 電子與信息學報, 2015, 37(4): 763-769. doi: 10.11999/JEIT140875.

XIA Shutao, LIU Lu, and LIU Xinji. Deterministic constructions of compressive sensing matrices based on berlekamp-justesen codes[J].&, 2015, 37(4): 763-769. doi: 10. 11999/JEIT140875.

[10] 趙瑞珍, 王若乾, 張鳳珍, 等. 分塊的有序范德蒙矩陣作為壓縮感知測量矩陣的研究[J]. 電子與信息學報, 2015, 37(6): 1317-1322. doi: 10.11999/JEIT140860.

ZHAO Ruizhen, WANG Ruoqian, ZHANG Fengzhen,. Research on the blocked ordered vandermonde matrix used as measurement matrix for compressed sensing[J].&, 2015, 37(6): 1317-1322. doi: 10.11999/JEIT140860.

[11] ZENG L, ZHANG X, CHEN L,. Deterministic construction of toeplitzed structurally chaotic matrix for compressed sensing[J].,,, 2015, 34(3): 797-813. doi: 10.1007/s00034-014- 9873-7.

[12] LI S and GE G. Deterministic sensing matrices arising from near orthogonal systems[J]., 2014, 60(4): 2291-2302. doi: 10.1109/ TIT.2014.2303973.

[13] MOHADES M M, MOHADES A, and TADAION A. A reed-solomon code based measurement matrix with small coherence[J]., 2014, 21(7): 839-843. doi: 10.1109/LSP.2014.2314281.

[14] YU N Y and GONG G. A new binary sequence family with low correlation and large size[J]., 2006, 52(4): 1624-1636. doi: 10.1109/ TIT.2006.871062.

[15] CHEN S S, DONOHO D L, and SAUNDERS M A. Atomic decomposition by basis pursuit[J]., 1998, 20(1): 33-61. doi: 10.1137/ S1064827596304010.

[16] TROPP J. Greed is good: algorithmic results for sparse approximation[J]., 2004, 50(10): 2231-2242. doi: 10.1109/TIT.2004.834793.

[17] DONOHO D L and ELAD M. Optimally sparse representation in general (nonorthogonal) dictionaries via1minimization[J]., 2003, 100(5): 2197-2202. doi: 10.1073/pnas. 0437847100.

[18] HAUPT J, BAJWA W U, RAZ G,. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]., 2010, 56(11): 5862-5875. doi: 10.1109/TIT.2010.2070191.

Construction of Compressed Sensing Measurement Matrix Based on Binary Sequence Family

LU Cunbo XIAO Song QUAN Lei

(,,’710071,)

It is significant to construct deterministic measurement matrix for the promotion and application of the Compressed Sensing (CS) theory. Originating from the algebraic coding theory, a construction algorithm of Binary Sequence Family (BSF) based deterministic measurement matrix is presented. The coherence is an important criterion to describe the property of matrices. Lower coherence leads to higher reconstruction performance. The coherence of the proposed measurement matrix is derived to be smaller than the corresponding Gaussian random matrix and Bernoulli random matrix. Theoretical analysis and simulation results show that the proposed matrix can obtain better reconstruction results than the corresponding Gaussian random matrix and Bernoulli random matrix. The proposed matrix can make the hardware realization convenient and easy by means of Linear Feedback Shift Register (LFSR) structures, thus being conductive to practical compressed sensing.

Signal processing; Compressed Sensing (CS); Measurement matrix; Binary Sequence Family (BSF)

TN911.72

A

1009-5896(2016)07-1682-07

10.11999/JEIT151076

2015-09-21；改回日期：2016-01-20；網絡出版：2016-03-25

蘆存博 444180647@qq.com

國家自然科學基金(61372069)，高等學校學科創新引智計劃(111計劃)(B08038)

The National Natural Science Foundation of China (61372069), The Programme of Introducing Talents of Discipline to Universities (111 Project) (B08038)

蘆存博： 男，1989年生，博士生，研究方向為無線網絡編碼、壓縮感知加密算法.

肖 嵩： 女，1977年生，教授，博士生導師，研究方向為網絡編碼、視頻/圖像聯合信源信道編碼.

權 磊： 男，1989年生，博士生，研究方向為無線傳感器網絡、壓縮感知.