LM算法求解大殘差非線性最小二乘問題研究

祝　強，李少康，徐　臻

（1.西安工業大學測試與控制技術研究所，陜西 西安 710021；2.西安共達精密機器有限公司，陜西 西安 710075）

LM算法求解大殘差非線性最小二乘問題研究

祝強1，李少康1，徐臻2

（1.西安工業大學測試與控制技術研究所，陜西 西安 710021；2.西安共達精密機器有限公司，陜西 西安 710075）

針對傳統LM算法求解大殘差非線性最小二乘問題時存在算法失效的現象，分析Hessian矩陣與其近似矩陣的相似度對LM算法有效性的影響，提出一種依據殘差變化方向搜索信賴域區間的自尋優LM算法。優化阻尼系數的更新算法，引入大殘差引起的局部不收斂判斷條件，以最速下降法結束當前迭代。迭代過程均以目標函數值的減小作為接受條件，算法穩定可靠。圓擬合測試結果證明:自尋優LM算法對待求參數初始值的選取不敏感，在15°夾角短圓弧、大殘差等極端條件下仍可獲得較快的收斂速度和良好擬合效果。自尋優LM算法具有較強的魯棒性和穩定性，性能明顯優于傳統LM算法。

LM算法；高斯牛頓法；最小二乘；殘差

0　引　言

在工程應用中，許多問題都可以歸結為非線性最小二乘問題的最優化實現，如圓擬合、非線性型面擬合。目前，大多數非線性最優化方法是把目標函數按Taylor級數進行展開，舍去高階項，將非線性目標函數近似線性化，通過迭代算法求解待求參數，使其不斷逼近最優目標。

常用算法有最速下降法、Newton法[1-2]、Gauss-Newton（GN）法、Levenberg-Marquardt（LM）算法等。最速下降法利用負梯度方向作為搜索方向，是一種非常穩定的算法，但收斂速度不能盡如人意。Newton法保留了目標函數Taylor級數展開式中的一階項和二階項，具有二次收斂速度，但每一步迭代都需要計算Hessian矩陣，計算繁瑣。GN法以目標函數的Jacobian矩陣來構造Hessian矩陣的近似矩陣H′，提高了算法效率。以上兩者具有相同的缺陷，若Hessian矩陣或其近似矩陣H′為奇異矩陣時，兩種算法都無法繼續迭代。

LM算法[3-4]屬于一種信賴域算法，由學者K. Levenberg以及D.Marquardt研究提出的，目的在于解決Hessian構造矩陣的非正定問題和奇異問題。LM算法主要用于求解非線性多元目標函數[5]的最優問題，目前對LM算法的研究主要集中在收斂速率和穩定性上，如利用外在曲率在傳統LM算法中加入輔助加速項[6-7]來提高LM算法的收斂速度。采用Sobolev梯度替代歐氏梯度[8-9]實現LM算法求解非線性最小二乘問題。通過分析和改進阻尼系數的更新策略[10-11]，使LM算法具有更強的適用性等。本文旨在分析殘差水平與算法穩定性之間的關系，特別是求解非線性最小二乘問題，待求參數初始值的選取對LM算法穩定性和收斂速度的影響，對阻尼系數和信賴域的更新策略進行改進，使之具有更強的穩定性。

1　LM算法推導及分析

1.1LM算法

以誤差平方和SSE構造最小二乘目標函數[5-6]F（x，w），表示為

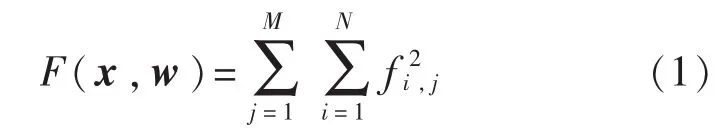
式中：x——輸入參數向量；

w——待求參數向量；

N——待求參數向量的個數；

f——目標函數單項殘差值；

M——離散非線性系統的采樣點個數。

令k為迭代步數，wk、wk+1分別為第k步、第k+1步迭代搜索到的待求參數值，待求參數取wk時，Jacobian矩陣表示為Jk，單項殘差值表示為fk，梯度向量表示為gk，Hessian矩陣表示為Hk，則Newton法迭代公式為

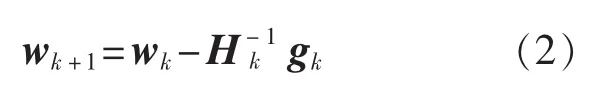
式（3）說明Newton算法以負梯度方向作為極小值的搜索方向，相比于最速下降法而言，其步長不再通過線性精確搜索獲得，而是采用Hessian矩陣的逆矩陣作為搜索步長，算法具有二次收斂速度。當矩陣H為奇異矩陣時，無法求得其逆矩陣，Newton法無法進行迭代。同時，Hessian矩陣的正定性是Newton法搜索方向正確的保證。

GN法的迭代公式為

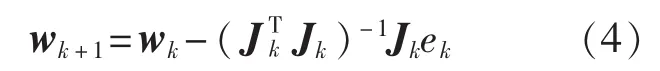
GN法以Jacobian矩陣來計算Hessian矩陣的近似矩陣，迭代過程中不再計算目標函數的二階偏導，算法效率得以提高。但兩者具有同樣的缺陷，當近似Hessian矩陣奇異或非正定時，算法無法執行或發散。

為了克服Newton法和GN法存在的缺陷，LM算法采用新的方法構造近似Hessian矩陣，保證算法的穩定性。LM算法迭代公式為

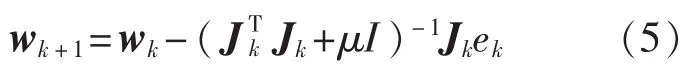
從迭代公式可以得出，LM算法是最速下降法和GN法的組合。阻尼系數μ相當于權值，當μ=0時，LM算法蛻化為GN法；當系數μ較大時，LM算法近似為最速下降法。系數μ的選擇保證了LM算法的有效性，避免近似Hessian矩陣不可逆情況的出現。LM算法的實現方式不是唯一的[7-8]，研究的主要內容集中在矩陣H的構造方法以及阻尼系數μ的更新公式上，但各種算法都是以學者D.Marquardt給出的LM算法為基礎，這里稱之為傳統LM算法。

1.2傳統LM算法在圓擬合中的應用分析

圓擬合[12-13]屬于非線性最小二乘問題，是工程應用中經常遇到的一種曲線擬合[14-15]，如回轉零件加工和測量中的坐標系建立、圓度測量等。圓擬合通常是在被測工件或裝置上對其某一截面進行采樣，獲取該截圓上的離散采樣點，通過優化算法進行圓擬合計算，得到圓心和半徑信息。

在理論半徑為100mm，采樣點數為11個，誤差水平±2μm條件下，采用傳統LM算法對不同采樣點中心夾角、不同初始值情況下進行擬合計算，分析殘差、夾角對算法帶來的影響。設定最大迭代次數為50次，當梯度向量的二范數或待求參數向量增量的二范數＜10-6時，迭代終止，仿真測試在Matlab中完成，測試結果如表1所示。表中“夾角”是指采樣點所含中心夾角大小，“初始值”是指算法選擇的待求參數初始向量，對于圓擬合，待求參數向量為（x，y，r），即圓心坐標和半徑。“擬合圓心”是指算法得到的圓心坐標（x，y）。傳統LM算法的圓擬合結果可以得出，當采樣點中心夾角較大、待求參數初始值接近理論值時，算法可以獲得較為理想的擬合結果。如夾角為90°、120°，初始值選取為[0，2，90]或[-2，2，60]時，傳統LM算法得到的擬合圓信息較為真實，擬合圓心及擬合半徑偏差符合圓擬合中疊加誤差與采樣夾角間的誤差傳遞關系。當初始值遠離理論值時，如[-20，20，10]，算法不能收斂，無法得到正確的圓信息。

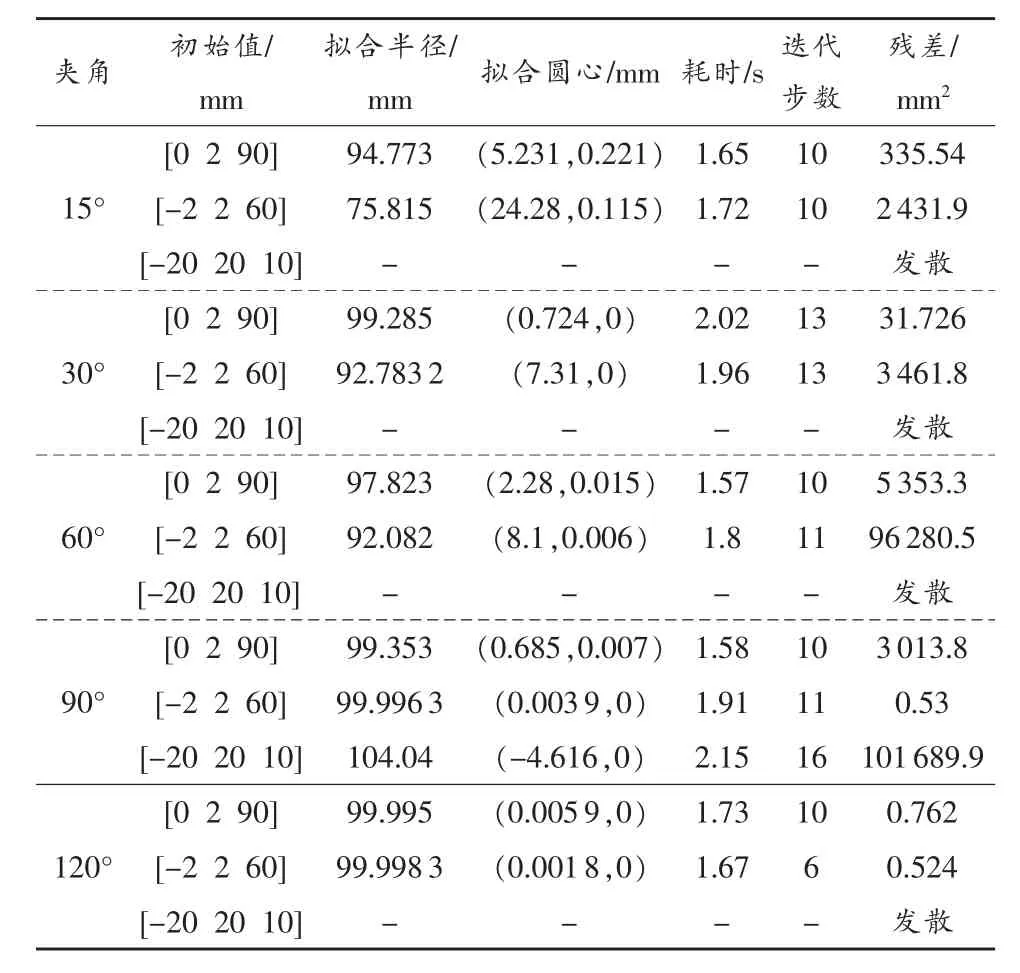
表1　傳統LM算法的圓擬合結果

從傳統LM算法推導過程分析，算法采用Jacobian矩陣來計算Hessian矩陣的近似矩陣，在流程中以增益系數λ的符號來判斷當前迭代點是否可以接受。也就是說，如果λ＞0，算法認為當前迭代點保證了目標函數的下降趨勢，并以增益系數λ來計算下一步迭代的阻尼系數μ。對殘差函數f（x+h）按Taylor級數展開，并忽略二階及以上項，可得：

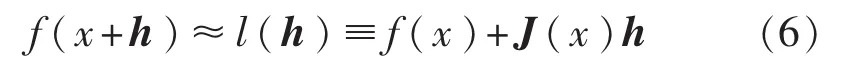
目標函數可近似表示為

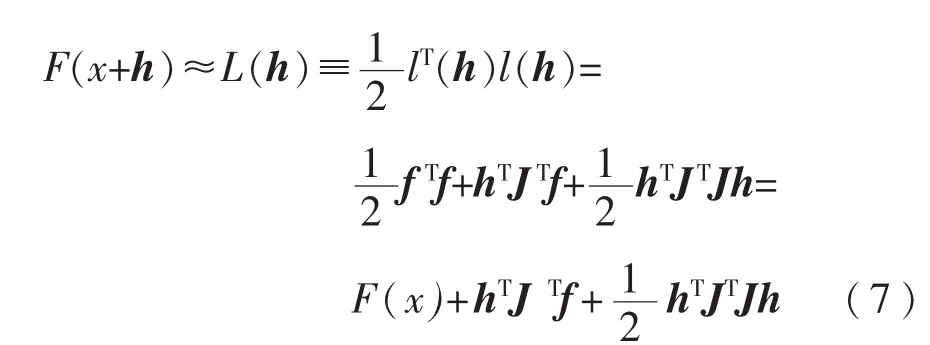
傳統LM算法中增益系數λ的計算如下式：

式（8）中分母項為

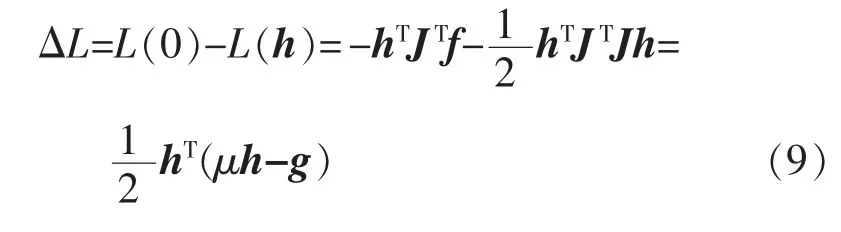
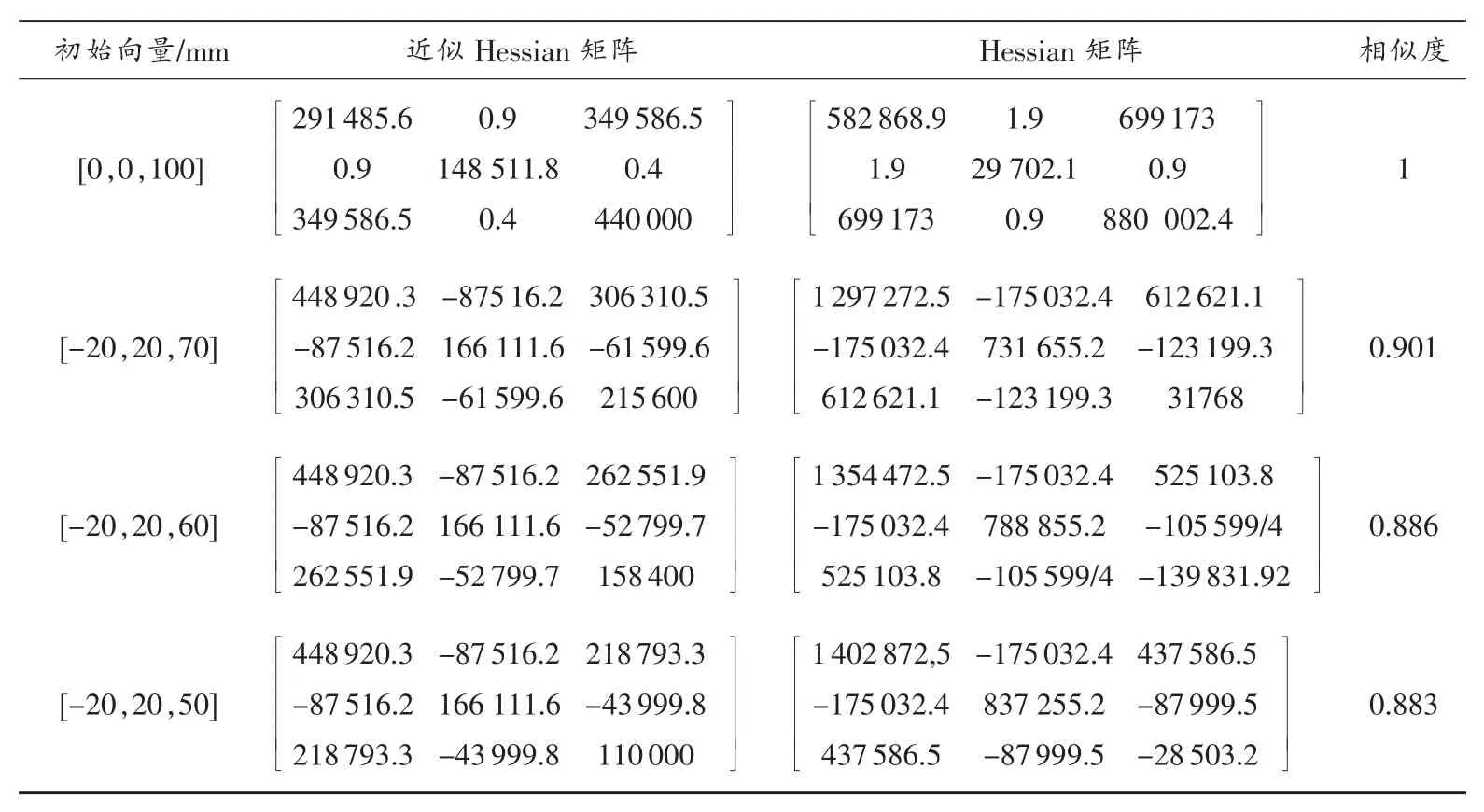
表2　初始向量選擇對Hessian矩陣及近似Hessian矩陣的影響

由于阻尼系數μ＞0，且hTh、-hTg為正，因此式（8）中的分母項必為正，這就是傳統LM算法采用增益系數λ的符號來判斷目標函數是否下降的原因。從上述推導過程可知，式（6）是該結論的基礎。但在實際應用中，由于待求參數向量的理論值無法預知，選定的初始值可能遠離理論值，從而導致采用線性模型來近似原目標函數不成立。在這種情況下，增益系數λ算式的分母項無法保證一定為正，傳統LM算法中對殘差變化方向的判斷和阻尼系數μ的預測都會失效。

Pi在孤獨而絕望的漂流中，選擇了信仰上帝，“信仰上帝就是敞開心胸，就是不受拘束，就是深深的信任，就是愛的自由行動”有時候他會疲憊、憤怒、和憂傷，他就會努力讓自己高興起來。他會摸著用襯衫碎片做的包頭巾大聲說：“這是上帝的帽子”；他會指著理查德·帕克大聲說“這是上帝的貓”；他會指著救生艇大聲說“這是上帝的方舟”；他會攤開雙手大聲說“這是上帝的寬廣土地”；他會指著天空大聲說“這是上帝的耳朵”就這樣，他一直提醒自己上帝的創造和自己在其中的位置。黑暗最終會消散，上帝會留下來，成為他心里一個閃光的點，他會繼續去愛，并因為對這世界的愛而活下去。

為了分析初始值偏離理論值的程度對傳統LM算法的影響，表2選取4種初始值向量，計算圓擬合目標函數對應的Hessian矩陣及其近似矩陣H（由Jacobian矩陣獲得），并給出兩者之間的相似度。表中理論圓圓心為（0，0），理論半徑為100mm。由相似度結果可知，當初始向量為[0，0，100]（向量元素依次為初始圓心坐標x、y，初始半徑r），即不含偏差時，兩者相似度為1。隨著初始值不斷偏離理論值，兩者之間的相似度不斷下降。

相似度變化表明傳統LM算法不適合解決大殘差條件下的非線性最小二乘問題，殘差較大時將導致目標函數的線性近似產生嚴重偏離，導致算法對殘差變化趨勢判斷出錯，造成阻尼系數μ的預測失敗，算法失穩。殘差較大時：1）計算目標函數的二階導數，LM算法蛻變為高斯牛頓法；2）改進阻尼系數的更新方法，提高LM算法的穩定性，在保持超線性收斂速度的同時，簡化算法的計算復雜度。

2　自尋優LM算法

通過以上分析和測試可知，當殘差較大時，傳統LM算法可能失效，算法無法獲得正確的圓擬合結果。針對這種情況，本文提出一種改進的自尋優LM算法，修正信賴域搜索條件，優化阻尼系數的更新方式，使LM算法具有更強魯棒性。算法流程如下：

1）初始化各變量，迭代步數k=0，確定待求參數向量初始值w0，設定迭代停止條件ε，最大迭代步數kmax。

2）計算Hessian近似矩陣H，H=JTkJk，計算梯度向量g，g=Jkfk。

3）第1步采用最速下降法計算下降方向h，采用一維準確線性搜索計算步長d，得到搜索點w1，w1=w0-d·h。迭代步數k=k+1，更新搜索點，w0=w1，計算H、g。

5）計算待求參數變化量h，h=-H-1g，更新搜索點w1=w0-h，計算目標函數值F1，令λmin=λ0，λ0=λ0+2λa，λmax=λ0，轉至6）。

6）如果F1≤F0，更新搜索點，w0=w1。迭代步數k= k+1，若k＞kmax，轉至11）。否則，轉至4）；如果F1＞F0，令Fmin=F1，轉至7）。

7）更新阻尼系數μ=（λmin+λmax）/2，Fold=F1，更新矩陣，計算待求參數變化量h，更新搜索點w′=w0-h，計算目標函數值F1。

8）如果 Fmin＞F1，置 Fmin=F1，λmin=λ0，num=0；否則，num=num+1；若num＞10，置ρ=1，轉9）；否則，轉至10）。

9）采用最速下降法替代本步迭代過程，計算迭代搜索點w1，w1=w0-d·h，更新搜索點，w0=w1，轉至4）。

10）如果Fold≤F1，搜索方向殘差增大，令λmax=λ0，λ0=λ0+λa/5，λmin=λ0，l=0，ν=2。如果Fold＞F1，搜索方向殘差減小，若l=1，令ν=2ν。更新變量λmin=λ0，λ0=λ0+ ν×λa，λmax=λ0，l=1。跳轉至6）。

11）結束迭代。

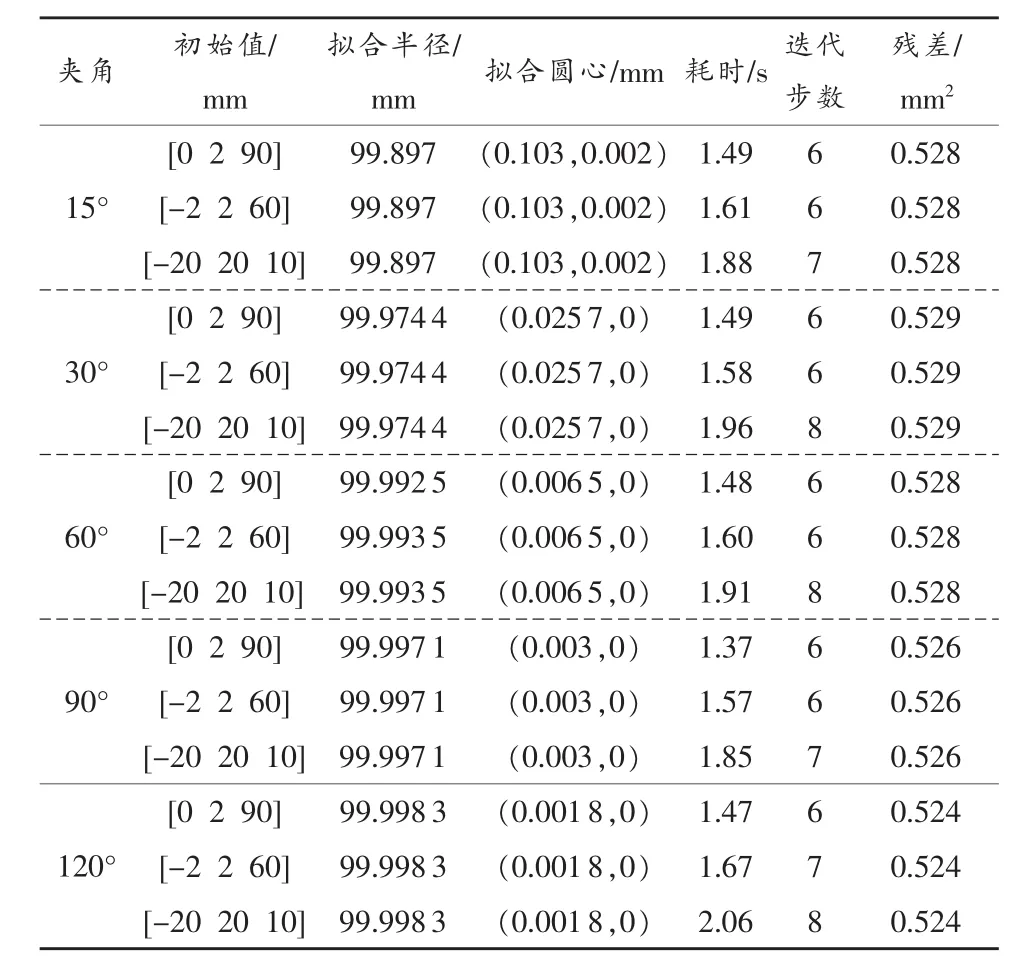
表3　自尋優LM算法的圓擬合結果

自尋優LM算法的每一步迭代過程均以目標函數值減小作為接受條件，確保殘差保持下降趨勢。阻尼系數μ的更新不再依賴于目標函數值的變化，而是在搜索過程中根據殘差變化方向進行修正，自動調整搜索范圍λmin、λmax，實現合理阻尼系數的快速搜索，避免了大殘差條件下產生錯誤的搜索方向。由于實際采樣點總會帶有一定的誤差，當誤差水平較高時，殘差會出現連續增大情況，表示無法很快找到合理的阻尼系數或當前搜索方向錯誤，阻尼系數的搜索耗時過長，算法將停止本次搜索，而改用最速下降法來計算本次迭代過程，保證算法的正常進行。

3　自尋優LM算法測試分析

為了測試自尋優LM算法在大殘差情況下的運行狀態，以表1中的測試條件進行仿真，對5種不同中心夾角和3種不同初始值情況下進行圓擬合計算，仿真結果如表3所示。

從表中測試結果來看，自尋優LM算法的穩定性明顯優于傳統LM算法，在初始值遠離理論值時仍然獲得了理想的圓擬合結果。當采樣點分布于中心夾角15°極端條件下，算法的擬合結果正確且穩定。從各種擬合條件下的測試結果來看，自尋優LM算法的迭代步數和計算時間基本恒定，目標函數的最終殘差值接近一致，即算法效率不受采樣條件和初始值選擇的影響，具有很強的魯棒性。

4　結束語

本文以圓擬合為例，分析了初始值選擇對Hessian矩陣及近似矩陣之間相似度的影響，證明了傳統LM算法不適合解決大殘差條件下的非線性最小二乘問題，從理論層面給出傳統LM算法失效的原因。文中提出自尋優LM算法，算法修正了尋找最優信賴域的條件，優化了阻尼系數的計算方法，提高LM算法的魯棒性。圓擬合仿真測試證明，自尋優LM算法的穩定性明顯優于傳統LM算法，算法效率不受初值的影響，在短圓弧、初值遠離理論值時均可獲得良好的擬合結果。

[1]WANG X H，LI C.Convergence of newton’s method and uniqueness of the solution of equations in banach space II[J].Acta Mathematica Sinica，2003，19（2）：405-412.

[2]PROINOV P D.General local convergence theory for a class of iterative processes and its applications to newton’s method[J].Journal of Complexity，2009，25（1）：38-62.

[3]MARQUARDT D W.An algorithm for the least-squares estimation of nonlinear parameters[J].Journal of the Society for Industrial and Applied Mathematics，1963，11（2）：431-441.

[4]LEVENBERG K.A method for the solution of certain non-linearproblemsinleastsquares[J].Quarterly Journal of Applied Mathmatics，1944，2（2）：164-168.

[5]魏榮，盧俊國，王執銓.基于Levenberg-Marquardt算法和最小二乘方法的小波網絡混合學習算法[J].信息與控制，2001，30（5）：440-442.

[6]TRANSTRUM M K，MACHTA B B，SETHNA J P, Why are nonlinear fits to data so challenging[J].Phys Rev Lett，2010（104）：060201.

[7]TRANSTRUMA M K，SETHNA J P.Improvements to the Levenberg-Marquardt algorithm for nonlinear leastsquares minimization[J].Journal of Computational Physics，2012，11（1）：1-32.

[8]RENKARJ.Nonlinearleastsquaresand Sobolev gradients[J].AppliedNumerical Mathematics，2013（65）：91-104.

[9]KAZEMIP，RENKARJ.ALevenberg-Marquardt method based on sobolev gradients[J].Nonlinear Analy sis：Theory，Methods&Applications，2012，75（16）：6170-6179.

[10]LAMPTON M.Damping-undamping strategies for the Levenberg-Marquardt nonlinear Least-Squares method[J]. Computers in Physics Journal，1997，11（1）：110-115.

[11]張鴻燕，耿征.Levenberg-Marquardt算法的一種新解釋[J].計算機工程與應用，2009，45（3）：5-8.

[12]UMBACH D，JONES K N.A few methods for fitting circlestodata[J].IEEE Trans on Instrumentation and Measurement，2003，52（6）：1181-1885.

[13]KANATANI K，SUGAYA Y.Performance evaluation of iterative geometric fitting algorithms[J].Computational Statistics&Data Analysis，2007，52（2）：1208-1222.

[14]ALSHARADQAH A，CHERNOV N.Error analysis for circle fitting algorithms[J].Electronic Journal of Statistics，2009，21（3）：886-911.

[15]CHERNOV N，LESORT C.Statistical efficiency of curve fitting algorithms[J].Computational Statistics and Data Analysis，2004，47（4）：713-728.

（編輯：莫婕）

Study of solving nonlinear least squares under large residual based on Levenberg-Marquardt algorithm

ZHU Qiang1，LI Shaokang1，XU Zhen2
（1.Institute of Measurement and Control Technology，Xi’an Technological University，Xi’an 710021，China；2.Xi’an GongDa Precision Machine Co.，Ltd.，Xi’an 710075，China）

The traditional Levenberg-Marquardt algorithm(LM algorithm)is always invalid in solving large residual nonlinear least squares problems.Thus,how the similarity between Hessian matrix and its approximate matrix influences the effectiveness of the traditional LM algorithm is analyzed.And a self-optimizing LM algorithm that the residual changing direction is used to search for trust-region intervals is proposed.The updating algorithm of damping coefficient is improved;A judging condition is introduced to solve the localdivergence caused by large residual;and the LM algorithm is substituted by the steepest descent method.It is the unique accepting condition that the objective function value is decreased continuously in the iterative process.The self-optimizing LM algorithm is stable and reliable.Circle fitting tests show that the self-optimizing LM algorithm is insensitive to the initial value of searching parameters.Under the extremeconditionssuchaslargeresidualandtheshortarcof15°includedangle,the convergence is fast and the fitting results are good,which proves that this new algorithm is robust and stable and its performance is superior to the traditional LM algorithm.

Levenberg-Marquardt algorithm；Gauss-Newton algorithm；least squares；residual

A

1674-5124（2016）03-0012-05

10.11857/j.issn.1674-5124.2016.03.003

2015-07-30；

2015-09-11

國家自然科學基金（51475351）；陜西省科學技術研究發展計劃項目（2013K08-12）；陜西省協同創新計劃項目（2015XT-32）；西安工業大學校長基金（XAGDXJJ1006）

祝強（1972-），男，湖北襄陽市人，副教授，博士，研究方向為精密測量與控制技術。