基于大衍數列的規則QC-LDPC碼構造方法
黃 勝,穆 攀,張 睿,袁建國
(重慶郵電大學 光通信與網絡重點實驗室,重慶 400065)
?
基于大衍數列的規則QC-LDPC碼構造方法
黃勝,穆攀,張睿,袁建國
(重慶郵電大學 光通信與網絡重點實驗室,重慶 400065)
結合楊輝三角的結構形式,基于大衍數列提出了一種列重為3或4的規則準循環低密度奇偶校驗(QC-LDPC)碼的新構造方法。該方法構造的校驗矩陣圍長至少為6,碼長可靈活變化,并且可節省存儲空間。仿真結果表明: 在相同的仿真參數下,當誤碼率(BER)為10-6時,所構造的列重為3的QC-LDPC(1260,620)碼的凈編碼增益(NCG)比二次函數碼改善了1 dB左右;列重為4的QC-LDPC(6056, 3028)碼相對于WMC-OCS、QC-OCS碼分別有0.1 dB和0.2 dB的NCG提升。
規則QC-LDPC碼; 楊輝三角; 大衍數列
低密度奇偶校驗碼(LDPC)是一類性能接近香農限、糾錯能力強的線性分組碼,自從它被重新發現以來,LDPC碼的設計、構造、分析、編譯碼器的實現以及在數字通信系統中的應用都已經成為了人們研究的焦點,成為Turbo碼的有力競爭者。LDPC碼的構造方法根據校驗矩陣的結構特點可分為兩種:隨機構造和代數構造。隨機構造法有Gallager構造[1]、Mackay構造[2]、Hu等人為盡可能增大圍長提出的經典PEG算法[3]等。這些基于計算機搜索構造出的碼字參數選擇靈活,性能優異。但是,隨機構造所產生的校驗矩陣沒有固定的結構,導致編碼復雜度高、存儲困難、硬件難以實現。為了克服隨機構造的這些缺點,代數的思想被納入到LDPC碼的構造中,人們提出了基于有限域[4]、有限幾何[5]、組合數學[6]等構造法,這些方法構造的碼字具有比隨機碼更低的編碼復雜度,尤其是具有循環或準循環特性的LDPC碼,已被廣泛應用于通信系統中。
近些年來,人們提出了許多基于組合數學構造LDPC碼的設計方案,比較典型的是BIBD構造法[7],此外,還有很多利用差集、數列等構造LDPC碼的方法[8-9]。根據大衍數列固定項差對應的值單調遞增的性質,朱磊基提出了一種基于大衍數列構造LDPC碼的方法[10],方法簡單,所構造的校驗矩陣具有準循環結構,長碼長的QC-LDPC碼具有優異的性能,但此方法只限于構造優異的長碼字。相對于長碼而言,中短碼的編譯復雜度低,被廣泛地應用于高速率無線通信及數據存儲通信等領域,因此對中短碼長的研究具有極好的理論和實踐意義。本文結合楊輝三角的構造形式,基于大衍數列提出了一種適宜于構造中短碼長的列重為3或4的規則QC-LDPC碼的新方法(簡稱為DY-QC-LDPC碼)。
1 融合大衍數列和楊輝三角的QC-LDPC碼構造
行重為L、列重為J、碼長N=P×L的(J,L)QC-LDPC的校驗矩陣可以表示為
(1)
式中:IPj,l為循環置換矩陣;Pj,l表示P×P的單位矩陣右移移位次數;Pj,l取值范圍為{0,1,…,P-1}或者∞,Pj,l=0時表示IPj,l為單位矩陣,Pj,l=∞時表示IPj,l為全零矩陣。
將校驗矩陣H中的循環置換矩陣用循環移位次數Pj,l表示,得到參數移位次數Pj,l構成的基矩陣P,為
(2)
當基礎矩陣確定后,QC-LDPC碼的校驗矩陣也就唯一確定了。校驗矩陣H中長度為2k的環可以由基矩陣P中長為2k的序列(Pj1,l1,Pj1,l2,Pj2,l1,…,Pjk,lk,Pjk,l1)表示,對于由循環置換矩陣擴展而成的QC-LDPC碼,Fossorier證明了長為2k的環存在的充要條件[11]為
(3)
式中:jk=j0,jb+1≠jb,lb+1≠lb,P為維數。不滿足式(3)則校驗矩陣中就不存在長為2k的環。
1.1楊輝三角
楊輝三角的構造簡單,是大家所熟知的一種數表,如圖1所示。
將楊輝三角沿著逆時針方向旋轉45°,可以得到

111121133114641..................
圖1楊輝三角

(4)
矩陣h具有這樣的特點:除第一行與第一列元素以外,其他位置的元素值均為位于本行、上一列的元素與本列、上一行的元素之和。若將這種結構運用到校驗矩陣中,只需要存儲校驗矩陣的第一行和第一列元素,其他元素可以通過簡單的加法計算得到,這樣能夠節省大量的存儲空間。若將h矩陣定義為校驗矩陣的基矩陣,h中的每個元素都代表著循環移位的次數,由fossorier定理可得擴展后的校驗矩陣中存在大量的四環,這會導致譯碼器不能快速收斂甚至不能收斂。所以,如何將楊輝三角這種簡單的構造運用到LDPC碼的中,并且使得校驗矩陣中不存在四環是需要考慮的一個重要問題。
1.2DY-QC-LDPC碼構造
對于一個數列f(n),若n取正偶數,f(n)=(n×n)/2,若n取正奇數,f(n)=(n×n-1)/2,滿足這樣條件的數列稱為大衍數列。結合楊輝三角的構造形式,基于大衍數列構造列重為3或4的規則QC-LDPC碼的步驟如下:
1)構造校驗矩陣的基矩陣:將基矩陣的第一行置0,第一列除首元素之外依次用大衍數列中的奇數項排列,第二行除首元素之外依次用大衍數列中的偶數項排列,其余位置上的元素采用楊輝三角形式構造。
2)由Fossorier定理檢測發現,基矩陣的第二行的前兩個元素與第三行的前兩個元素構成了四環的存在,這里將第二行的首元素0改為1,這樣可以避免四環的出現。
3)基矩陣擴展成校驗矩陣,具體方法是:將基矩陣中的0元素用單位矩陣替換,將非零元素用相應的移位循環矩陣替換。
由步驟1)基矩陣的構造方法可以看出:編碼器只需要存儲第一、二行與第一列的元素,其他位置元素可以通過簡單的加法計算得到,這樣有利于減少存儲空間。基矩陣中的各位置上的元素值如式(5),在基矩陣上進行擴展,可以構造出性能優異的中短碼長碼字。
(5)
式(5)中,對Pj,l=Pj-1,l+Pj,l-1歸納總結得
(6)
P3,l=l[f(3)+f(2)]+f(5)+(l-lk+1)f(2lk),
2≤lk≤l
(7)
根據構造規則,式(6)易得。式(7)成立的證明如下:
1)當l=1時,左式=P3,l=l[f(3)+f(2)],與實際相符。
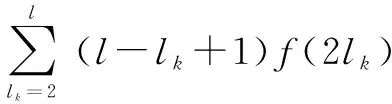
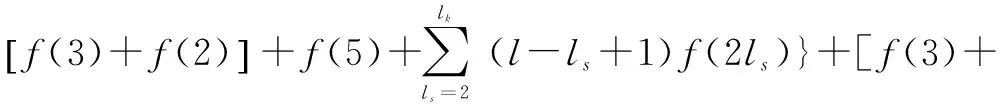
綜上,式(7)得證。
2 環分析
新方法構造的基矩陣的行、列上的元素滿足這樣的兩個特點:1)除第一行以外,每行的元素依次呈遞增關系;2)每列元素從上到下依次呈遞增關系。校驗矩陣不含四環,滿足式(8),其中j0≠j1,l0≠l1。
Pj0,l0-Pj1,l0+Pj1,l1-Pj0,l1≠0 modP
(8)
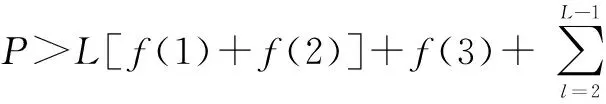
1)j0位于第0行、j1位于其他行
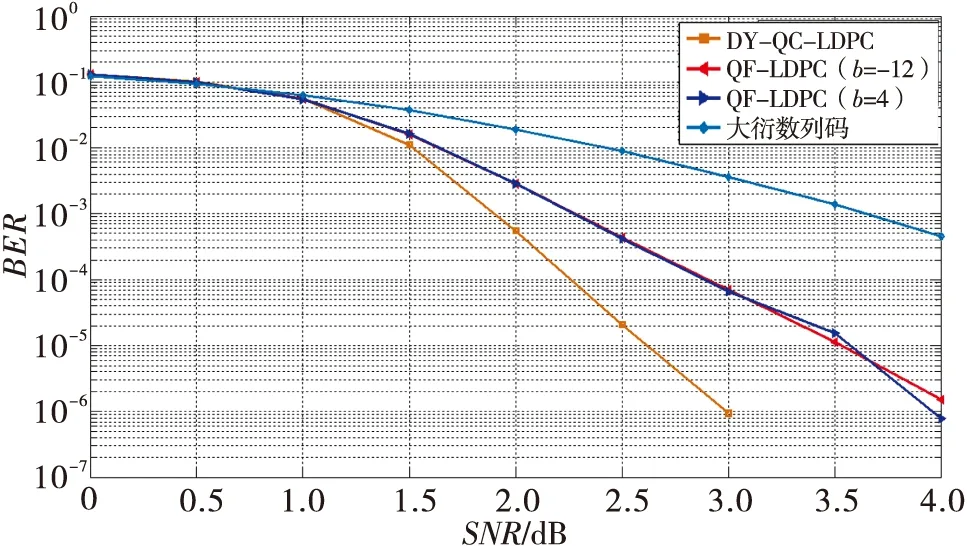
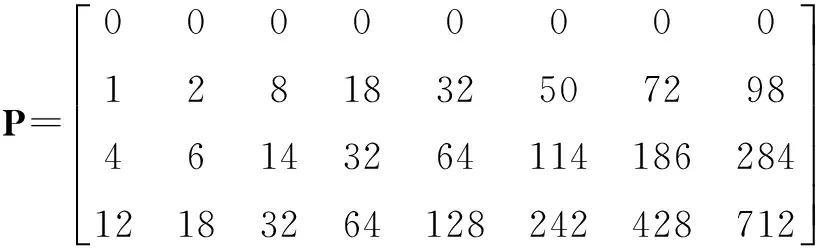
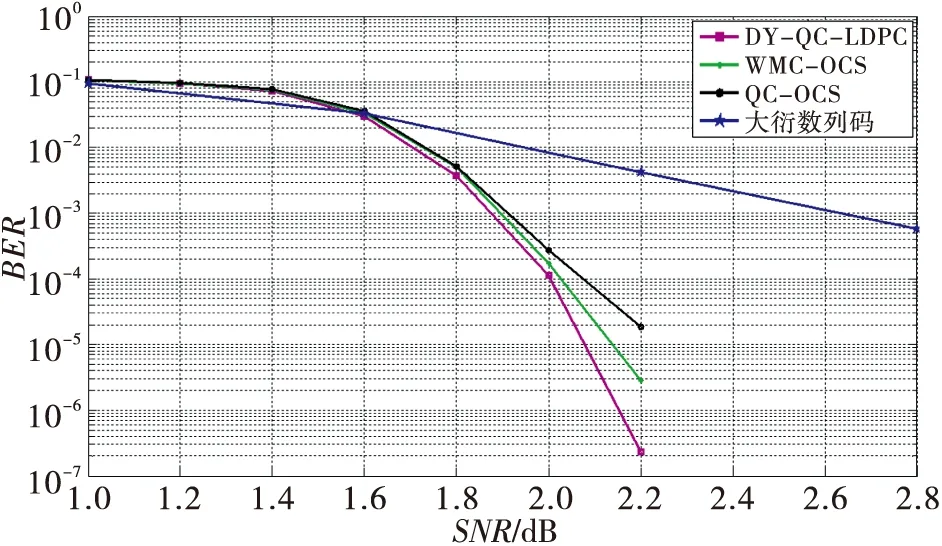
Pj0,l0-Pj1,l0+Pj1,l1-Pj0,l1=Pj1,l1-Pj1,l0 (9) 2)j0位于第一行、j1位于第二行 P1,l0-P2,l0+P2,l1-P1,l1=f(2l0)-[f(3)+ (10) 3)j0位于第一行、j1位于第三行 P1,l0-P3,l0+P3,l1-P1,l1=f(2l0)-f(2l1)+{l1[f(3)+ (11) 4)j0位于第二行、j1位于第三行 (12) 綜上可知:本文構造的(4,L)QC-LDPC碼的校驗矩陣中不含四環,(3,L)QC-LDPC碼中不含四環的證明與上類似。 本節給出DY-QC-LDPC碼在相同參數條件下同其他QC-LDPC碼的性能對比,選取1/2碼率、BP譯碼算法、BPSK調制方式、最大迭代次數40次,在AWGN信道下進行仿真實驗。首先給出列重為3的DY-QC-LDPC碼的性能,以(3,6)DY-QC-LDPC碼為例,該碼的基矩陣為 (13) 將基矩陣中的0元素用維數為210×210的單位矩陣替換,其他位置用對應的循環置換矩陣替換。圖2給出了相同的碼長、碼率以及仿真環境下,DY-QC-LDPC(1260,630)碼與大衍數列碼[10]和兩類二次函數碼(QF-LDPC)[12]的性能對比。由圖可以明顯地看出大衍數列不適合構造短碼長的碼字,DY-QC-LDPC碼性能優于二次函數碼。在誤碼率為10-6時,DY-QC-LDPC碼比QF-LDPC的兩種碼字性能提高約1 dB左右,具有更好的糾錯性能。 圖2 列重為3的DY-QC-LDPC(1 260, 630)碼和其他碼的性能比較 式(10)給出了(4,8)DY-QC-LDPC碼的基礎矩陣,將基礎矩陣中的元素用相應的757×757的循環移位矩陣替換,可以得到碼長為6 056的DY-QC-LDPC碼。圖3給出了DY-QC-LDPC(6 056, 3 028)碼和相同參數(碼長、碼率以及仿真環境)下的其他碼字性能對比。在誤碼率為10-6時,DY-QC-LDPC碼相對于文獻[13]中所提出的WMC-OCS和QC-OCS碼分別有0.1dB、0.2dB的凈編碼增益,且沒有明顯的錯誤平層。同時由大衍數列碼的仿真曲線可以看出文獻[10]中的構造方法也不適合于中碼長碼字的構造。 (14) 圖3 列重為4的DY-QC-LDPC(6 056, 3 028)碼和其他碼的性能比較 結合楊輝三角結構,本文基于大衍數列構造出了一種圍長至少為6、列重為3或4的規則DY-QC-LDPC碼。準循環特性使得它易于硬件實現,并且由于基矩陣的構造借鑒了楊輝三角的結構形式,所以編碼器只需要存儲0元素以及大衍數列的項,其他元素可以根據其位置通過簡單的加法計算得到,這樣可節省存儲空間。在相同的參數條件下,與大衍數列碼、QF-LDPC、WMC-OCS和QC-OCS碼相比,仿真結果表明中短長度的DY-QC-LDPC碼具有優異的糾錯性能。 [1]GALLAGERG.Low-densityparity-checkcodes[J].IEEEtransactionsoninformationtheory, 1962, 8(1):21-28. [2]MACKAYDJC.Gooderror-correctingcodesbasedonverysparsematrices[J].IEEEtransactionsoninformationtheory, 1999, 45(2):399-431. [3]HUXY,ELEFTHERIOUE,ARNOLDD.M.Regularandirregularprogressiveedge-growthtannergraphs[J].IEEEtransactionsoninformationtheory, 2005, 51(1):386-398. [4]HUANGS,TIANFF,JIAXT.AnovelconstructionmethodofLDPCcodesoverfinitefieldintheopticalcommunicationsystem[J].Actaphotonicasinica, 2014,43(6):1-4. [5]HUANGQ,DIAOQJ,LINS.CyclicandQuasi-CyclicLDPCcodesonconstrainedparity-checkmatricesandtheirtrappingsets[J].IEEEtransactionsoninformationtheory, 2012, 58(5):2648-2671. [6]YUANJG,LICY,HUANGS,etal.AnovelconstructionmethodofQC-LDPCcodesforopticalcommunicationsbasedontheBIBDandcirculantdecomposition[J].Journalofoptoelectronics·laser, 2013, 24(9):1698-1701. [7]LAN L, TAI Y Y, LIN S. New constructions of quasi-cyclic LDPC codes based on special classes of BIBD's for the AWGN and binary erasure channels[J]. IEEE transactions on communications, 2008, 56(1):39-48. [8]ESMAEILI M. 4-Cycle free LDPC codes based on difference sets[J]. IEEE transactions on communications, 2012, 60(12):3579-3586. [9]ZHANG L J, LI B. Constructions of QC LDPC codes based on integer sequences[J]. Science China, 2014, 57(6):1-14. [10]ZHU L J, WANG H, SHI Y S. Method for constructing QC-LDPC codes using the dayan sequence[J]. Journal of Xidian University, 2012, 39(3):144-160. [11]FOSSORIER M P C. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE transactions on information theory, 2004, 50(8):1788- 1793. [12]ZHANG G H, SUN R. Deterministic construction of girth-eight (3, L) QC-LDPC codes from quadratic function[J]. Electronics letters, 2013,49(9):600-602. [13]HUANG J F, HUANG C M, YANG C C. Construction of one-coincidence sequence quasi-cyclic LDPC codes of large girth[J]. IEEE transactions on information theory, 2012, 58(3):1825-1836. 黃勝(1974— ),教授,主要研究方向為信道編碼和下一代網絡; 穆攀(1990— ),女,碩士生,主研信道編碼; 張睿(1991— ),女,碩士生,主研信道編碼; 袁建國(1968— ),教授,主要研究方向為光通信技術與光電子技術。 責任編輯:薛京 Method of construction of regular QC-LDPC codes based on Dayan sequence HUANG Sheng, MU Pan, ZHANG Rui, YUAN Jianguo (KeyLaboratoryofOpticalCommunicationandNetwork,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China) According to structure of Yanghui Triangle and based on the Dayan sequence, a novel construction method of regular quasi-cyclic low-density parity-check (QC-LDPC) codes whose column weight is 3 or 4 is put forward. Girth of parity-check matrix is at least 6. Length of the code can vary flexibly. And storage spaces can be saved. Under the same parameters, at the bit error rate(BER) of 10-6, simulation results show QC-LDPC(1260, 620)code with column weight 3 has a net coding gain(NCG) nearly 1 dB more than quadratic function code and the NCG of QC-LDPC(6056, 3028) code with column weight 4 is 0.1 dB and 0.2 dB more than WMC-OCS and QC-OCS code respectively. regular QC-LDPC code; Yanghui triangle; Dayan sequence TN911 A 10.16280/j.videoe.2016.09.015 國家自然科學基金項目(61171158);重慶市自然科學基金項目(cstc2013jcyjA40052;cstc2012jjA40060);重慶市教委科學技術研究項目(KJ130515) 2016-01-08 文獻引用格式:黃勝,穆攀,張睿,等. 基于大衍數列的規則QC-LDPC碼構造方法[J]. 電視技術,2016,40(9):77-80. HUANG S, MU P, ZHANG R,et al. Method of construction of regular QC-LDPC codes based on Dayan sequence [J]. Video engineering,2016,40(9):77-80.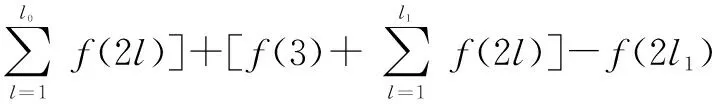
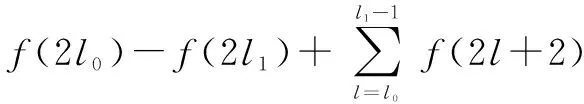
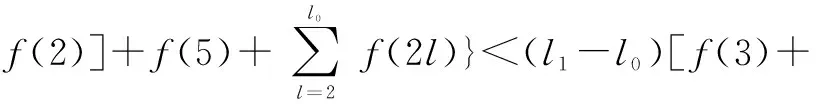
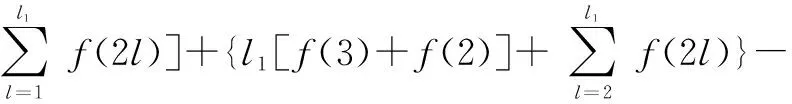
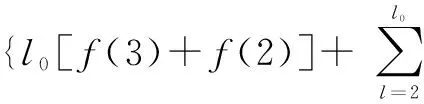
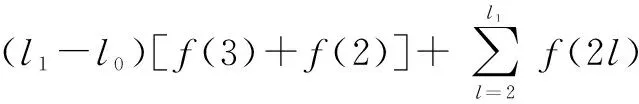
3 仿真分析

4 總結

