帶有動態誤差角補償的PMSM新型轉子位置觀測器

陸　駿，楊建國，馬胤琛

（東華大學 機械工程學院，上海 201620）

帶有動態誤差角補償的PMSM新型轉子位置觀測器

陸駿，楊建國，馬胤琛

（東華大學 機械工程學院，上海 201620）

在凸極永磁同步電機的幾種觀測模型中，等效反電勢模型結構簡單、不依賴轉子轉速、對電機參數不確定性的敏感度較低，也不受積分器引起的各項誤差影響。在等效反電勢模型的基礎上，提出了一種帶有動態誤差角補償的新型轉子位置觀測器。利用滑模觀測器來估計等效反電勢，提取含有誤差項的轉子位置信息。動態誤差角補償器進一步減少了定子直軸電流變化率引起的轉子位置估計誤差，改善了凸極永磁同步電機直接轉矩控制系統的無傳感器位置估算性能。相比于沒有補償動態誤差角的觀測器，提出的新型觀測器具有如下優點：1）針對DTC系統轉矩響應速度快的特點，新型觀測器提高了在轉速或負載瞬變情況下位置動態觀測精度；2）針對DTC系統電流諧波大的特點，新型觀測器減少了電流諧波引起的觀測誤差，提高了轉速穩態時的位置觀測精度。通過實驗證明了該觀測器的可行性和有效性。

永磁同步電機；滑動模態；轉子位置觀測；直接轉矩控制；誤差補償

0　引言

永磁同步電機PMSM（Permanent Magnetic Synchronous Motor）具有結構簡單、體積小、損耗小、效率高等優點，廣泛應用于工業生產、國防和日常生活等領域。永磁同步電機是一個全封閉整體直驅系統，其調速系統需要通過在電機軸上安裝速度和位置傳感器來實現，同時也帶來了以下問題：1）受溫度、濕度、檢測距離、振動等使用條件的限制，特別是在一些對檢測精度要求較高的場合，傳感器對工作條件有更苛刻的要求，從而限制了PMSM在這一些特殊領域的應用，使得安裝有此類傳感器的驅動系統不能適用于各種場合；2）傳感器的安裝加大了電機的體積和空間尺寸，同時也增加了系統的轉動慣量；3）為了保證測量精度，傳感器的安裝和維護要求也較高，這就增加了驅動系統的復雜性、降低了系統可靠性，同時提高了成本。因此，永磁同步電機無傳感器控制成為了電機控制領域的研究熱點，特別是在國防科技領域等的現代機電控制系統中占有重要位置。國內外已有很多關于無傳感器矢量控制［1］和直接轉矩控制［2］系統的研究成果面世，特別是直接轉矩控制技術DTC（Direct Torque Control）近年來引起了業界研究人員的高度關注，掀起了研究熱潮。無傳感器DTC的關鍵技術是通過電流位置模型實現定子磁鏈和轉矩的準確估計，所以轉子位置觀測器必須具有優異的動態及穩態觀測精度。

許多學者已經提出了以下多種估算轉子位置和速度的方法［3～8］：定子磁鏈估算法、模型參考自適應法、狀態觀測法、高頻注入法、人工智能估算法等。總的來說，可以將它們分為兩類：基于電機模型和基于外界激勵的轉子位置估算法。前者可簡單地通過觀測電機反電勢來估算轉子位置，已廣泛應用于隱極電機的中高速無傳感器運行。然而，由于凸極PMSM轉子存在凸極效應，其轉子位置估計算法一般來說比隱極PMSM要復雜得多。為了實現基于電機模型的凸極PMSM轉子位置估計，通常需要把模型進行重構，轉化為等效的隱極PMSM模型。目前的文獻中，可以將此類重構的模型分成三種：拓展反電勢（extended electromotive force，EEMF）模型［9］、有效磁鏈（active flux，AF）模型［10］和等效反電勢模型［11］。EEMF模型需要轉子速度信息和電機參數，如：定子電阻和定子電感，且受定子交軸電流變化率影響，因此很難設計此類觀測器來同時滿足抗負載擾動和電機參數不確定的魯棒性。有效磁鏈模型一般會采用積分器來計算磁鏈項，在此情況下會產生一些較難解決的實際問題，比如：電流傳感器的直流偏置、積分器的直流偏置、累計誤差和初始狀態等。與EEMF模型和AF模型相比，等效反電勢模型不受較多電機參數及轉速等影響，也不受積分器引起的各項誤差影響。但是該模型在推導過程中，忽略了定子直軸電流的微分項。因此，當電機處于變速及變載運行狀態或者電流存在諧波時，基于該模型構建的轉子位置觀測器的動態精度會降低。直接轉矩控制的特點是轉矩動態響應快，但其定子磁鏈畸變和轉矩脈動相對較大，相應的定子相電流諧波也較大，因此在變速變載及轉速穩態運行時，定子直軸電流的微分項較大，產生的位置觀測誤差也較大。

為了實現高性能的無傳感器DTC轉速閉環控制，本文在等效反電勢模型的基礎上，提出了一種帶有動態誤差角補償的新型轉子位置觀測器。利用滑模觀測器來估計等效反電勢，提取含有誤差項的轉子位置信息。動態誤差角補償器進一步減少了定子直軸電流變化率引起的轉子位置估計誤差，改善了凸極永磁同步電機直接轉矩控制系統的無傳感器位置估算性能。基于TI公司DSP（TMS320F2812）進行實驗，驗證了該觀測器的優異性能。

1　基于等效反電勢的轉子位置觀測器構建

1.1基于等效反電勢的PMSM模型

在αβ- 坐標系下，基于等效反電勢的PMSM定子電壓電流模型為：

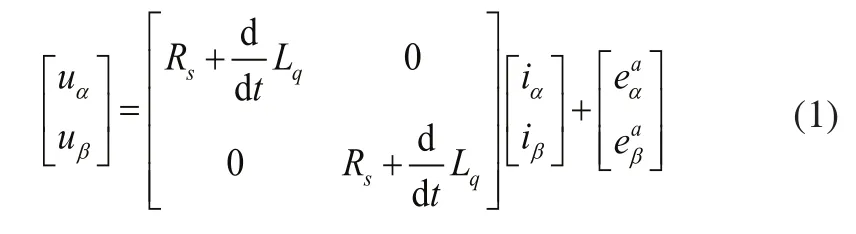
等效反電勢的定義模型為：

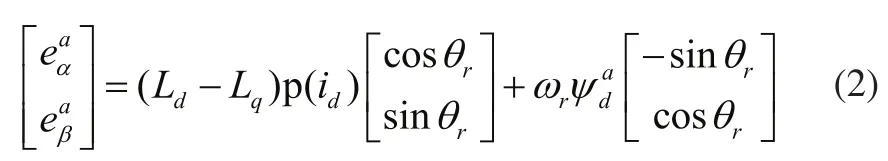
式中：p為微分算子；id為定子電流直軸分量；θr

為轉子電角度；Ld為直軸電感；ωr為轉子電角速度；

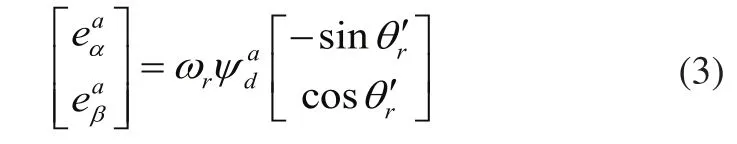
從等效反電勢的簡化模型可知，它的α和β分量分別是轉子位置的正弦和余弦函數，通過反正切函數tan-1

1.2滑模觀測器的設計與穩定性證明

為使轉子位置觀測具有強魯棒性，根據等效反電勢模型，可設計滑模觀測器［12～14］的狀態空間方程為：

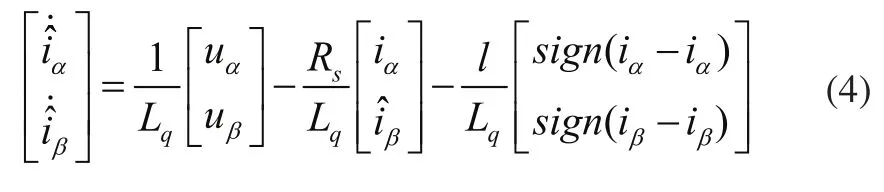
將式（4）與式（1）相減后，可得等效反電勢模型的電流誤差狀態空間方程為：

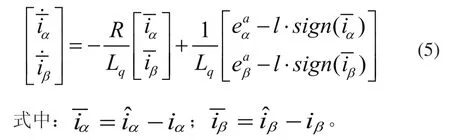
構建李雅普諾夫能量方程為：

為使系統狀態變量在平衡點附近漸進穩定，必須滿足：

由于滑模增益過大會引起抖振，因此可根據實際效果選擇適當的l值。當系統進入滑動模態時，通過低通濾波從滑模切換函數的高頻開關信號中提取等效控制函數，即為等效反電勢，從而得出轉子位置信息為：

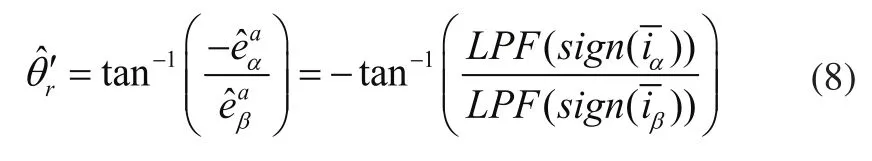
圖1為所提出的滑模觀測器結構框圖。

2　動態誤差角的分析與補償

等效反電勢模型雖然克服了EEMF模型和AF模型的部分缺點，但存在直軸電流微分項引起的動態誤差角，需要對其進行補償以提高了轉子位置的動態觀測精度。

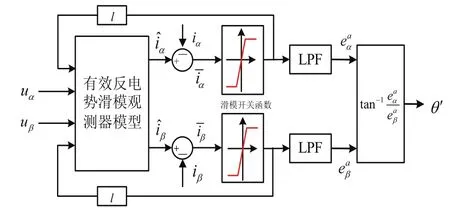
圖1　滑模觀測器結構框圖

2.1動態誤差角的分析

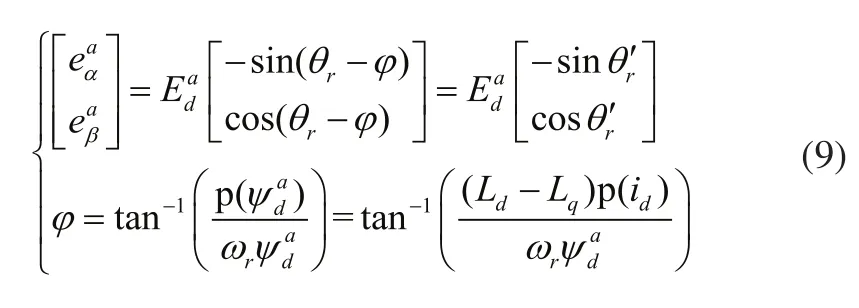
由上式可見，通過等效反電勢的反正切函數直接得出凸極PMSM的θ'r與實際轉子位置θr之間存在一個動態誤差角φ，假設id的微分值極小時，則φ幾乎為零。在某些特定條件下該假設近似成立，例如采用轉矩電流正比策略的矢量控制時，id的設定值為零，其變化率相對較小。然而在實際應用中該假設很難成立，尤其是采用最大轉矩電流比策略的矢量控制或者直接轉矩控制等。當轉速或者負載突變以及電流諧波分量較大時，id變化率較大，動態誤差角φ并不完全等于零，且轉速越低、負載越大時，φ越大。由于θ'r并不是實際轉子位置θr的精確估算量，因此本文提出了一種動態誤差角補償器，降低了轉子位置觀測值與實際位置的偏差，提高在轉速或負載瞬變以及電流存在諧波情況下的轉子位置估算性能。

2.2動態誤差角的補償

根據前文討論可知，θr與φ的差值θ'r可通過滑模觀測器求得，rω為θr的求導函數。另外，在φ的模型中，利用Park變換將id轉化為θr的函數，則φ也成為θr的函數。由此，可通過式（10）的方程組得出轉子實際位置θr和動態誤差角φ：

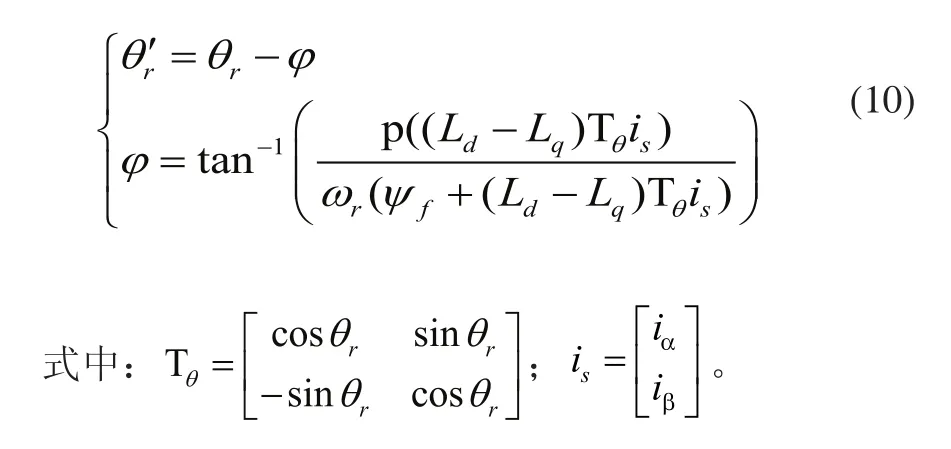
為實現上述方程組的求解，本文所提出的動態誤差角補償器結構框圖如圖2所示。該動態誤差角補償器利用圖1所示滑模觀測器得出的作為已知輸入量，當θr的動態誤差角φ，通過PI調節器自動跟蹤φ的實際值。其調節參數需要根據φ的變化特性，使其達到良好的跟蹤效果。

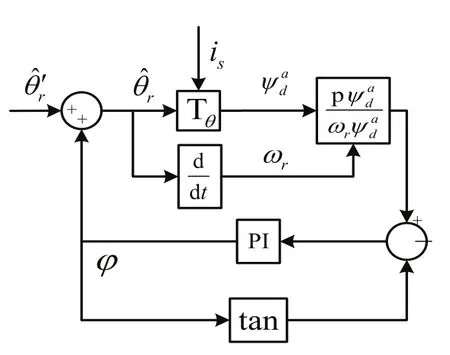
圖2　動態誤差角補償器

3　實驗結果分析

為了檢驗新型轉子位置觀測器的準確性，將其作為冗余傳感器在PMSM-DTC轉速閉環控制系統上進行實驗，圖3是該實驗平臺系統組成圖。該系統中的永磁同步電機增量式編碼盤為2500線，逆變器開關頻率為16k，控制電路的數字信號處理芯片是TI公司的TMS320F2812。DSP自帶的A/D數模轉換器分辨率為12位。可調直流電源與磁滯離合器組成了可調負載機構。

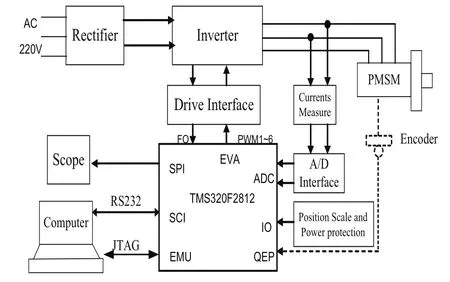
圖3　實驗平臺系統組成圖

實驗所用電機參數如表1所示。

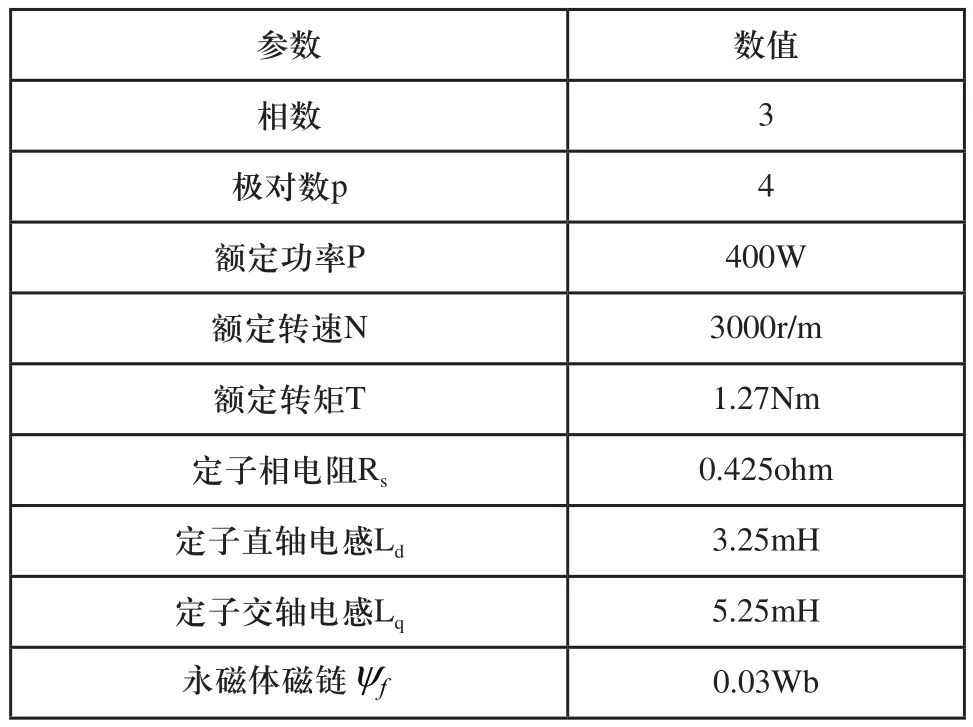
表1　電機參數

在變速和變載實驗中，將電機實際位置和新型位置觀測器估算結果之差作為觀測精度，并與現有文獻［11］中的無補償觀測器作對比，驗證了帶有動態誤差角補償器的新型位置觀測器的優異性能。

1）變速實驗

圖4顯示了電機在變速實驗過程中的轉速變化曲線，電機在恒定0.1Nm負載下，從200r/min加速后達到300r/min，而后又減速到200r/min。圖5是該過程中補償前與補償后的位置觀測誤差比較圖。從圖5可以看出，當轉速從200r/min升至300r/min的動態過程中，補償前的動態誤差為0.29rad，補償后的動態誤差為0.11rad。當轉速從300r/min降至200r/min的動態過程中，補償前的動態誤差為0.38rad，補償后的動態誤差為0.12rad。在200r/min的穩定轉速下，補償前的諧波誤差為0.08rad，補償后的諧波誤差為0.04rad。在300r/min的穩定轉速下，補償前的諧波誤差為0.07rad，補償后的諧波誤差為0.034rad。可見，電機轉速越低，動態誤差角越大，與其理論模型保持一致。更多結果表明，補償后的觀測器在電機的不同工作點始終具有更高的穩態和動態觀測精度。

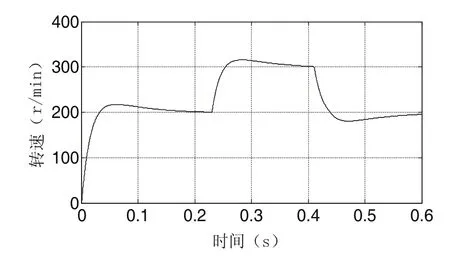
圖4　變速實驗電機轉速曲線

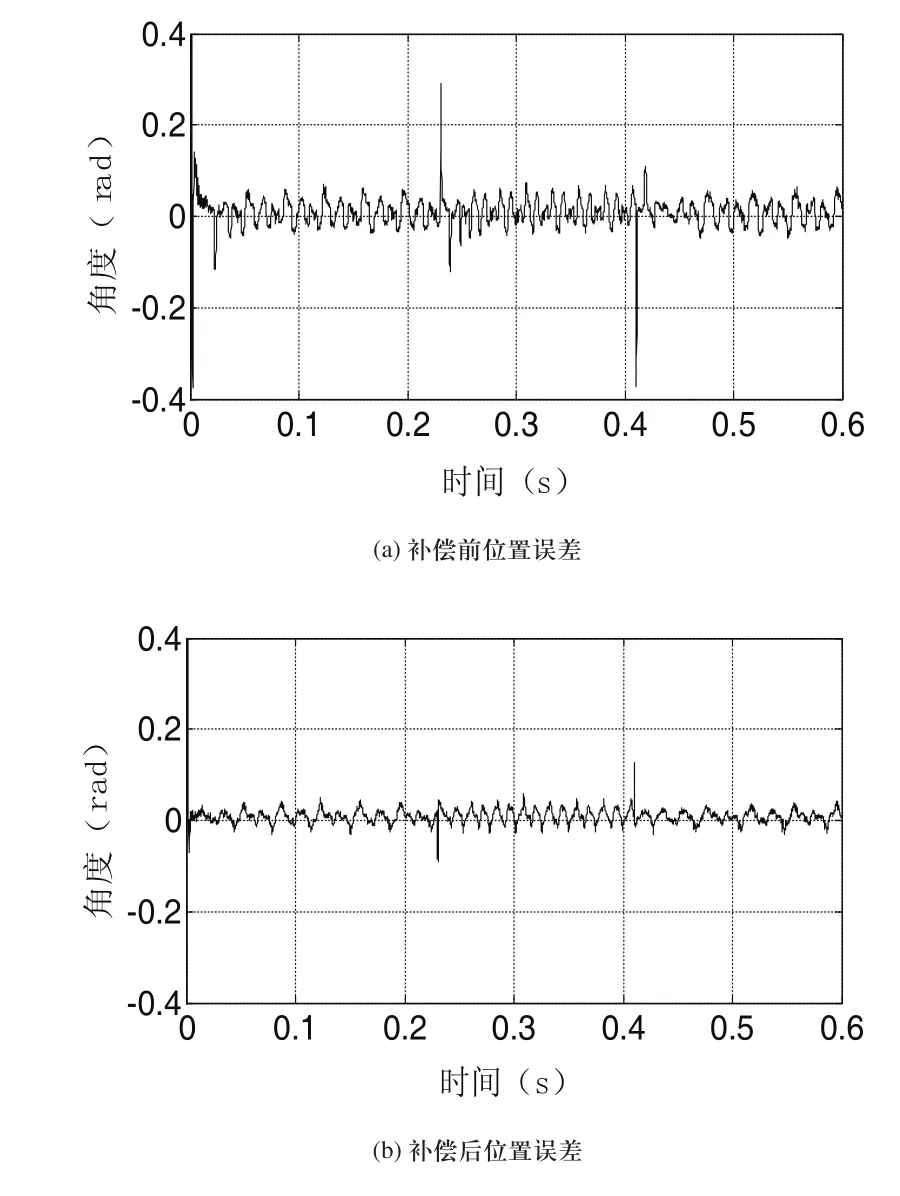
圖5　變速實驗補償前后轉子位置觀測誤差比較

2）變載實驗

圖6顯示了電機在變載實驗過程中的轉矩變化曲線，電機在600r/min穩定轉速下，從0.1Nm加載后達到0.5Nm，而后又減載回0.1Nm。圖7是該過程中的補償前與補償后的位置觀測誤差比較圖。從圖7可以看出，當負載從0.1Nm加載后達到0.5Nm的動態過程中，補償前的動態誤差為0.11rad，補償后的動態誤差為0.036rad。當負載從0.5Nm減載后達到0.1Nm的動態過程中，補償前的動態誤差為0.054rad，補償后的動態誤差為0.031rad。在600r/min的穩定轉速下，負載為0.1Nm時補償前的諧波誤差為0.048rad，補償后的諧波誤差為0.032rad；負載為0.5Nm時補償前的諧波誤差為0.083rad，補償后的諧波誤差為0.046rad。可見，電機負載越大，動態誤差角越大，與其理論模型保持一致。更多結果表明，補償后的觀測器在電機的不同工作點始終具有更高的穩態和動態觀測精度。

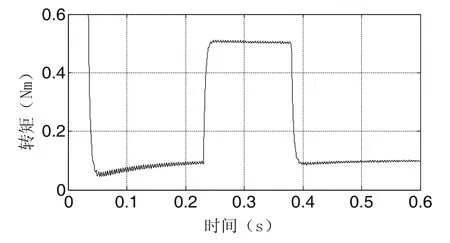
圖6　變載實驗電機輸出轉矩曲線

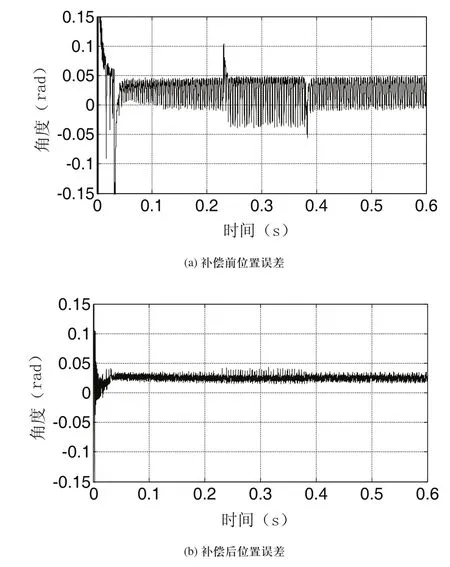
圖7　變載實驗補償前后轉子位置觀測誤差比較

然而，在低于30r/min的實驗中，由于定子電阻變化等影響，反電動勢的估算已經相當困難，從而導致觀測器誤差過大甚至失效［15］。

4　結論

本文在凸極永磁同步電機等效反電勢模型的基礎上，提出了一種帶有動態誤差角補償器的新型轉子位置滑模觀測器，改善了凸極PMSM直接轉矩控制系統的無傳感器位置估算性能。

本文提出的新型觀測器補償了直軸電流微分項引起的動態誤差角，相比于沒有補償動態誤差角的觀測器，它具有如下優點：1）針對DTC系統轉矩響應速度快的特點，新型觀測器提高了在轉速或負載瞬變情況下位置動態觀測精度；2）針對DTC系統電流諧波大的特點，新型觀測器減少了電流諧波引起的觀測誤差，提高了轉速穩態時的位置觀測精度。

由于本文提出的新型轉子位置觀測器仍然依賴電機的基波模型，因此在低速或零速時由于定子電阻變化等影響而很難估算反電動勢，使得觀測結果誤差很大甚至失效，必須采用高頻信號注入法等其他方式來實現無傳感器控制。

［1］ 田清.采用交叉耦合補償的異步電動機矢量控制系統研究［J］.制造業自動化，2011，33（4）:37-39.

［2］ 李曉竹，姚剛.基于MATLAB/Simulink的BLDC直接轉矩控制系統仿真［J］.制造業自動化，2011，（17）:129-131.

［3］ 劉毅，賀益康，秦峰，賈洪平.基于轉子凸極跟蹤的無位置傳感器永磁同步電機矢量控制研究［J］.中國電機工程學報，2005，25（17）:121-126.

［4］ 尹忠剛，劉靜，鐘彥儒，楊立周.基于雙參數模型參考自適應的感應電機無速度傳感器矢量控制低速性能［J］.電工技術學報，2012，（7）:124-130.

［5］ 滕青芳，柏建勇，朱建國，郭有光.基于滑模模型參考自適應觀測器的無速度傳感器三相永磁同步電機模型預測轉矩控制［J］.控制理論與應用，2015，32（2）:150-161.

［6］ Quang Nguyen Khanh，Hieu Nguyen Trung，Ha Q.P..FPGA-based sensorless PMSM speed control using reduced-order extended kalman filters［J］.IEEE Transactions on Industrial Electronics，2014，61（12）:6574-6582.

［7］ Maurizio Cirrincione，Marcello Pucci.An MRAS -Based Sensorless High-Performance Induction Motor Drive with a Predictive Adaptive Model［J］.IEEE Transactions On Industrial Electronics，2005，52（2）:532-551.

［8］ 秦峰，賀益康，劉毅，章瑋.兩種高頻信號注入法的無傳感器運行研究［J］.中國電機工程學報，2005，25（5）:116-121.

［9］ S. Morimoto，K. Kawamoto，M. Sanada，and Y. Takeda. Sensorless control strategy for salient-pole PMSM based on extended EMF in rotating reference frame［J］.IEEE Trans. Ind. Appl.，2002，38（4）:1054-1061.

［10］ I. Boldea，M. C. Paicu，and G. D. Andreescu.Active flux concept for motion sensorless unified ac drives［J］.IEEE Trans. Power Electron.，2008，23（5）:2612-2618.

［11］ Liu Jingbo，Nondahl Thomas A.，Schmidt Peter B.，Royak Semyon，Harbaugh Mark.Rotor position estimation for synchronous machines based on equivalent EMF［J］.IEEE Transactions on Industry Applications，2011，47（3）:1310-1318.

［12］ Hosseyni Anissa，Trabelsi Ramzi，Mimouni Med Faouzi，Iqbal Atif，Alammari Rashid.Sensorless sliding mode observer for a five-phase permanent magnet synchronous motor drive［J］.ISA Transactions，2015，58:462-473.

［13］ Foo Gilbert，Rahman M.F..Sensorless sliding-mode MTPA control of an IPM synchronous motor drive using a sliding-mode observer and HF signal injection［J］.IEEE Transactions on Industrial Electronics，2010，57（4）:1270-1278.

［14］ Wang Gaolin，Li Zhuomin，Zhang Guoqiang，Yu Yong，Xu Dianguo. Quadrature PLL-based high-order sliding- mode observer for IPMSM sensorless control with online MTPA control strategy［J］. IEEE Transactions on Energy Conversion，2013，28（1）:214-224.

［15］ M.C. Paicu，I. Boldea，G.-D.Andreescu，F. Blaabjerg.Very low speed performance of active flux based sensorless control: interior permanent magnet synchronous motor vector control versus direct torque and flux control［J］.IET Electr. Power Appl.，2009，3（6）: 551-561.

A novel rotor position observer of PMSM with dynamic error compensation

LU Jun，YANG Jian-guo，MA Yin-chen

TM301.2

A

1009-0134（2016）09-0009-05

2016-05-23

國家科技重大專項（2013ZX04001-141）

陸駿（1985 -），男，江蘇人，博士，研究方向為無傳感器電機控制。