南昌紅谷隧道E4管節軸線糾偏案例的分析與應用

邢永輝， 張　毅， 李志軍

(1. 中鐵隧道勘測設計院有限公司， 天津　300133； 2. 廣州打撈局， 廣東 廣州　510260；3. 中鐵隧道集團二處有限公司， 河北 三河　065201)

?

南昌紅谷隧道E4管節軸線糾偏案例的分析與應用

邢永輝1， 張毅2， 李志軍3

(1. 中鐵隧道勘測設計院有限公司， 天津300133； 2. 廣州打撈局， 廣東 廣州510260；3. 中鐵隧道集團二處有限公司， 河北 三河065201)

南昌市紅谷隧道沉管段全長1 329 m，分為12節管節，是目前國內內河最長的沉管隧道工程，其管節安裝的軸線精度控制是工程施工的重點及難點。為保證管節安裝精度，同時兼顧經濟性、便捷性和可行性，以本工程管節安裝為例，對管節安裝的主要影響因素進行計算，提出利用現有橫調系統對管節安裝軸線進行糾偏的方案。理論計算與實測數據對比表明，提出的方案可對管節安裝軸線進行有效的糾偏，對其他沉管隧道工程也可起到一定的借鑒作用。

沉管隧道; 管節沉放; 管節安裝; 軸線糾偏

0　引言

自1894年美國在波斯頓修建世界上第一座沉管隧道以來，截至2008年，中國、美國、荷蘭、丹麥、挪威和日本等20多個國家已建成了100多條沉管隧道[1-2]，并在近幾年呈快速增長態勢。沉管法作為一種先進的隧道施工方法發展至今，已有了成熟的施工工藝。其主要施工工序有： 管節主體預制、基槽開挖、管節沉放安裝、基礎處理、最終接頭處理和管內鋪裝等。管節沉放安裝作為施工過程中極其重要的一環，其軸線精度直接關系到管節能否順利合攏，是沉管法隧道施工中的重點和難點。

目前國內外常用的沉管法隧道管節安裝軸線糾偏方法主要有管節安裝前的預判糾偏及管節安裝后的實測糾偏。

管節安裝前的預判糾偏方法主要為接頭橫向錯位法[3]，即根據上一管節的實測安裝偏差，計算待安裝管節的糾偏幅度，通過改變接頭導向裝置的軸線來實現管節軸線橫向平移錯位的目的，在上海外環隧道、南昌紅谷隧道和越南西貢隧道等工程得到了廣泛的應用。

管節安裝后的實測糾偏又分為管內糾偏、管外糾偏及重新對接調整[4]，管內糾偏方法主要為頂頭擺尾法，即通過在接頭設置千斤頂、楔形塊[5]等使接頭不均勻對接，從而達到調整管尾軸線的目的，在日本多摩川隧道[6]、港珠澳大橋隧道[7]等工程應用了此法； 管外糾偏方法主要為管外頂推法，即通過在管外設置千斤頂、絞車等使管節平移或偏轉以達到調整軸線的目的，如韓國釜山—巨濟隧道采用的EPS(Eternal Lifting & Positioning System)調整系統等； 而重新對接調整法由于涉及到GINA止水帶二次壓縮、管節間碰撞等不利因素，因此通常不作為首選糾偏方法。

本文運用糾偏方法的原理，對南昌紅谷隧道E4管節現場實際偏差情況進行分析，在盡可能不增加設備的情況下，通過既有的管節橫調系統對管節安裝軸線進行糾偏，可兼顧經濟性、便捷性和可行性。

1　工程概況

南昌市紅谷隧道工程是目前國內最長的內河沉管法隧道工程。本工程沉管段總長1 329 m，共分為12節管節，最終接頭設置于E10-1管節與E10-2&E11管節之間。管節長度為90～115 m、高度為8.3 m、寬度為30 m、質量為22 000～28 000 t； 管頭中部設置1處導向裝置，管尾兩側各設置1處水下垂直千斤頂，3點形成管節沉放對接豎向支撐體系； 管面利用絞車及滑輪組等形成管節縱調、橫調系統。

2015年8月進行了本工程E4管節沉放安裝，并進行了E4管內軸線精確測量，測量結果如表1所示。

表1　E4管節測量數據

根據E4管節軸線測量數據，若不采取任何措施，E5、E6管節將順著E4管節軸線射線方向安裝，即：

E5管尾預計偏移量=19.3 mm+ 40.4 mm(E4管尾偏移量)=59.7 mm；

E6管尾預計偏移量=19.3 mm+ 59.7 mm(E5管尾偏移量)=79 mm。

上述預測值已嚴重超出設計要求，因此必須對管節軸線進行糾偏。

2　E4管節軸線糾偏相關計算

影響管節安裝軸線的主要因素分布示意圖如圖1所示。

圖1　管節軸線影響因素分布圖(單位： m)

Fig. 1Influencing factors of axial line deviation of tunnel segment (m)

2.1垂直千斤頂摩擦力

1)穩定壓載前。管節沉放時負浮力為2 744 kN(280 t)，管節初步落座后，根據支承墊塊位置(距管頭105 m)與管節長度(115 m)關系，計算得導向裝置提供支撐力1 244.6 kN，垂直千斤頂提供支撐力1 499.4 kN，在高應力下假定鋼-鋼靜摩擦因數為0.12，計算得垂直千斤頂摩擦力=1 499.4 kN×0.12=179.9 kN，對管頭導向裝置力矩=179.9 kN×105 m =18 889.5 kN·m。

2)穩定壓載后。管節穩定壓載負浮力13 720 kN(1 400 t)，同理可得垂直千斤頂摩擦力=899.6 kN，對管頭導向裝置力矩=899.6 kN×105 m=94 458 kN·m。

2.2水壓力

2015年8月28日隧址水位為12.65 m，預計E5管節沉放時水位位于12～12.5 m，如圖2所示，管節所受水壓力水平合力為管頭面積所受水壓力。

圖2　管節受水壓力水平分力示意圖

E4管節水壓力F由F1、F2組成(如圖3所示)，計算公式如下：

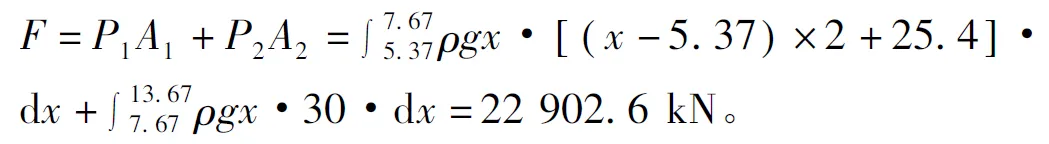
式中： P1為F1部分的水壓壓強； A1為F1部分的面積； P2為F2部分的水壓壓強； A2為F2部分的面積； x為計算點水深； ρ為水體密度，取1t/m3； g為重力加速度，取9.8m·s-2。

同理，根據E5管頭底標高0.13m及E5管節沉放預計水位12～12.5m，計算得E5管節平均理論水壓力約19 600kN。

圖3　E4管節橫斷面示意圖(單位： m)

2.3拉合千斤頂及橫調纜拉力

1)目前使用的拉合千斤頂系統可提供拉力為980kN(100t)/臺(受拉桿強度制約)，即2臺拉合千斤頂總共可提供1 960kN拉力。拉合千斤頂距離導向裝置支點8.315m，即，單邊拉力產生的力矩=980kN×8.315m=8 148.7kN·m。

2)目前使用的橫調系統主要包括10t液壓絞車、80t吸附式重力錨塊及5輪滑車組，可提供784kN(80t)拉力(受錨塊制約)，對導向裝置力矩=784kN×105m=82 320kN·m。

2.4碎石鎖定回填側壓力

由于垂直千斤頂摩擦力較大，因此按靜止土壓力計算碎石鎖定回填側壓力

碎石鎖定回填對導向裝置力矩=74.52kN×85m=6 334.2kN·m。

式中： γ為碎石水下重度，取6kN/m3； h為碎石回填高度，取3m； k0為靜止土壓力系數，按松散砂土取0.46； l為碎石回填寬度，取6m。

2.5水流力計算

式中： F為水流力； Cw為水阻力系數，取2.0； ρ為水密度，取1t/m3； v為水流速度，取0.3m/s； A為迎流面積。

水流力對導向裝置力矩

式中：f為dx范圍內的水流力；x為f至導向裝置的距離。

2.6GINA止水帶相關計算

2.6.1壓縮曲線

GINA止水帶壓縮曲線如圖4所示。

圖4　GINA止水帶壓縮曲線

2.6.2理論反彈力及理論壓縮量

E3/E4接頭GINA止水帶實測壓縮量為113.75 mm(8月28日)，根據壓縮曲線可得GINA止水帶反彈力約為375 kN/m，理論總反彈力=375 kN/m×71 m(GINA止水帶總長度)=26 625 kN。

根據E4管節水壓力22 902.6 kN，考慮管頭導向裝置及管尾垂直千斤頂摩擦力1 646.4 kN(=13 720 kN×0.12)，計算GINA止水帶反彈力=22 902.6+1 646.4=24 549 kN，與理論總反彈力存在2 076 kN誤差，分析原因是由于GINA止水帶壓縮量測量誤差及壓縮曲線觀測誤差導致。

根據E5管節預計平均水壓力19 600 kN及GINA止水帶壓縮曲線，反推E4/E5接頭GINA止水帶理論壓縮量為103 mm。

2.6.3GINA止水帶不均勻壓縮分析

1)根據E4管節軸線狀態，為保證E5管節軸線偏轉至與原設計軸線方向，E5管尾需偏轉約3.8 cm，即 E4/E5接頭GINA止水帶須產生1 cm不均勻壓縮。

2)由于GINA止水帶兩側壓縮量相差僅1 cm，因此假設該范圍內的GINA止水帶壓縮量與反彈力呈線性關系。

3)基于以上假設，E4/E5接頭GINA止水帶北側理論壓縮量為98 mm，對應的反彈力為230 kN/m； 南側理論壓縮量為108 mm，對應的反彈力為325 kN/m，詳見圖5。

圖5　GINA止水帶不均勻壓縮反彈力示意圖(單位： kN/m)

Fig. 5Sketch diagram of uneven nonuniform compression elastic strength of GINA water seal strip (kN/m)

4)GINA止水帶造成的回復力矩(轉點為導向裝置)

式中： 8 m=扣除管節倒角影響后的側墻高度； 47.5 kN/m=(南側墻反力-北側墻反力)/2=(325 kN/m-230 kN/m)/2； 14.725 m為力臂，取(管節寬度-鋼端殼寬度)/2=(30 m-0.55 m)/2； 13.75 m=頂底板長度和/4=(25 m+30 m)/4。

2.7適用的平均水深臨界值計算

2.7.1現有橫調系統(784 kN拉力)糾偏3.8 cm工況

通過2.1、2.3中的計算可得，現有橫調系統提供的對導向裝置拉力矩為82 320 kN·m，千斤頂摩擦力產生的阻力矩為18 889.5 kN·m，即臨界狀態下的止水帶不均勻壓縮回復力矩=82 320-18 889.5=63 430.5 kN·m。

通過2.6中的回復力矩計算公式及圖4中的GINA止水帶壓縮曲線計算，可得兩側GINA止水帶的反彈力分別為534、358 kN/m，對應的極限壓縮量分別為121、111 mm。

糾偏前的平均極限壓縮量=(121+111)/2=116 mm，根據圖4可得對應的反彈力為419.8 kN/m，總反彈力=419.8×71(GINA止水帶總長度)=29 805.8 kN，即水壓力29 805.8 kN。

通過2.2中的計算方法反算可得，管頭橫斷面形心處的極限水深為12.5 m。

2.7.2加強橫調系統(1 470 kN拉力)糾偏3.8 cm工況

通過加大絞車、錨塊和滑輪組等措施，將橫調纜拉力提升至1 470 kN，即橫調系統提供的對導向裝置拉力矩為1 470 kN×105 m=154 350 kN·m，千斤頂阻力矩為18 889.5 kN·m，即臨界狀態下的止水帶不均勻壓縮回復力矩=154 350-18 889.5=135 460.5 kN·m。

同理可得兩側GINA止水帶的反彈力分別為837、481 kN/m，對應的極限壓縮量分別為129、119 mm。

糾偏前的平均極限壓縮量=(129+119)/2= 124 mm，對應反彈力為630.5 kN/m，總反彈力=水壓力=630.5×71=44 765.5 kN，可得管頭橫斷面形心處的極限水深為18.8 m。

2.7.3現有橫調系統(784 kN拉力)糾偏1.9 cm工況

按上述方法計算可得兩側GINA止水帶的反彈力分別為673、502 kN/m，對應的極限壓縮量分別為125、120 mm。糾偏前的平均極限壓縮量=122.5 mm，對應反彈力為582.2 kN/m，總反彈力=水壓力=582.2×71=41 336.2 kN，可得管頭橫斷面形心處的極限水深為17.4 m。

3　E4管節糾偏案例的分析及應用

3.1糾偏案例的主要原理

管節水壓接后穩定壓載前，利用管尾橫調纜調整管節軸線，再利用穩定壓載加大管尾垂直千斤頂摩擦力來置換橫調纜錨泊力，最后松橫調纜，達到軸線糾偏的目的，其本質屬于管外頂推法。

3.2糾偏案例的施工方案

本工程管節沉放時采用的管外測量系統為全站儀+測量塔，受測量塔剛度、水流力、風力、管面及測量塔控制點放樣、管節橫傾和縱傾等一系列因素的影響，管外測量系統與管內精確測量存在一定誤差，因此本案例的施工方案采用管節對接完成并打開水密門后的管內測量數據作為糾偏依據。具體糾偏方法： 按常規方法沉放—管外測量配合橫調纜調整管節軸線—管節落座—水壓接—打開水密門—管內軸線測量—管內測量配合管尾橫調纜調整管節軸線—穩定壓載—鎖定回填—松管尾橫調纜—管內測量復核。

3.3可行性分析及主要結論

計算數據匯總詳見表2。

表2　計算數據匯總表

1)管節穩定壓載前，千斤頂摩擦力矩與止水帶回復力矩之和小于橫調纜拉力矩，因此認為通過橫調纜調節管節軸線是可行的(力矩： ⑤>①+⑧)。當水深逐步增大時，止水帶不均勻壓縮回復力矩也將隨之增大，需根據工程實際情況分析其是否可行，可通過加強橫調系統或減少糾偏值來提高其適用范圍。

2)管節穩定壓載后，橫調纜拉力矩小于千斤頂摩擦力矩，因此認為此時通過橫調纜調節管節軸線是不可行的(力矩： ⑤<②)。

3)管節穩定壓載后，止水帶回復力矩小于千斤頂摩擦力矩，因此認為此時松橫調纜是可行的(力矩： ⑧<②)。

4)水壓力計算應當計算管頭水壓力。

5)由于鎖定回填側壓力遠小于垂直千斤頂摩擦力，且鎖定回填通常在管節落座并穩定壓載后才進行，因此認為鎖定回填意義不大(力矩： ⑥?②)。

6)由于拉合千斤頂拉力矩與止水帶回復力矩相差太大，因此認為利用拉合千斤頂輔助調整GINA帶壓縮偏差是不可行的(力矩： ④?⑧)。

7)由于水流力遠小于垂直千斤頂摩擦力，因此本文認為在管節落座后，水流力(0.3 m/s)不會影響管節軸線(力矩： ⑦?①)，但水流速度較快時要根據實際情況重新評估，且應該考慮鎖定回填由靜止土壓力轉換為被動土壓力時帶來的積極效果。

8)本文主要為理論計算，實際施工時應根據現場情況變化、設備效率和安全要求等因素，制定分階段糾偏計劃，將偏差調整分布到各個管節，盡量避免在一節管上完成所有偏差的糾偏。

3.4糾偏案例的特點及適用范圍

1)經濟、操作簡單，無需額外增加設備，僅對原工序作局部調整。

2)軸線偏差可調幅度中等，且受水深影響較大，水深較淺時適應性較好，對于本工程： 管底水深16.5 m時，管尾軸線可調幅度約4 cm，與整體錯位法配合時可調幅度達6 cm； 管底水深21.4 m時，管尾軸線可調幅度約2 cm，與整體錯位法配合時可調幅度達4 cm； 相對于±3.5 cm的設計軸線精度要求，有足夠的控制力。當水深大于21.4 m時，在不調整橫調系統的情況下，本案例的糾偏方案不適用。

3)不受沉管段總長度影響，但沉管段總長度較長、管節較多時優勢明顯。

4)每節管節沉放時均可使用，可避免管節軸線產生較大的累計偏差。

4　結論及討論

E4管節實測安裝軸線為偏北約40 mm，后續的E5管節、E6管節按上述方案進行糾偏后，實測E6管節安裝軸線為偏北約20 mm，較預計的79 mm調整了59 mm，證明通過既有橫調系統進行管節安裝軸線糾偏的設想是切實可行的。

管節沉放對接軸線偏差控制是沉管法隧道，尤其是長距離沉管法隧道施工的重難點。采用經濟、簡單、可行的方法將管節沉放對接軸線偏差進行分節糾偏，避免產生較大累計偏差是本文的主要理念。由于本案例采用簡化的邊界條件進行理論分析，且各個隧道施工工況多少存在差異，使得本案例提出的施工方案存在一定的局限性，本案例采用的糾偏方案需打開水密門后安排管內測量人員輔助糾偏，相對于橫向錯位法、EPS體外調整等方法來說存在一定的風險，因此，在不同的沉管法隧道工程施工過程中，應盡可能采用橫向錯位法等風險較低的糾偏方法，確實需要采用本案例類似的糾偏方法時，應深入分析現場實際情況，將施工經驗與理論計算相結合，形成針對性較強、安全性較高的糾偏方案，并在實施過程中加強管節姿態監測，以確保施工安全。

[1]程樂群,劉學山,顧沖時.國內外沉管隧道工程發展現狀研究[J].水電能源科學，2008, 26(2): 112-115.(CHENG Lequn, LIU Xueshan, GU Chongshi. Research on development of immersed tunnel engineering at home and abroad[J]. Water Resources and Power, 2008, 26(2): 112-115.(in Chinese))

[2]馬建, 孫守增, 趙文義,等. 中國隧道工程學術研究綜述·2015[J]. 中國公路學報, 2015, 28(5): 1-65.(MA Jian, SUN Shouzeng, ZHAO Wenyi, et al. Review on China’s tunnel engineering research·2015[J]. China Journal of Highway and Transport, 2015, 28(5): 1-65.(in Chinese))

[3]潘永仁, 楊我清. 沉管隧道平面軸線控制與調整方法探討[J]. 現代隧道技術, 2004, 41(3): 62-65.(PAN Yongren, YANG Woqing. Discussion on the horizontal alignment of immersed tube tunnel[J]. Modern Tunnelling Technology, 2004, 41(3): 62-65. (in Chinese))

[4]孫召才. 沉管隧道軸線控制和調整技術研究[D]. 廣州： 華南理工大學, 2014. (SUN Zhaocai. Study of immersed tunnel axis control and adjustment technology[D]. Guang-zhou: South China University of Technology, 2014. (in Chinese))

[5]馬宗豪, 孫健, 管澤旭. 沉管隧道管節線形控制方法[J]. 中國港灣建設, 2014(11): 12-15. (MA Zonghao, SUN Jian, GUAN Zexu. Liner control method of immersed tube tunnels[J]. China Harbour Engineering, 2014(11): 12-15. (in Chinese))

[6]胡政才, 先明其. 日本多摩川沉管隧道的設計與施工[J]. 世界隧道, 1995(5): 52-75. (HU Zhengcai, XIAN Mingqi. Design and construction of Tamagawa Immersed Tunnel[J]. Tunneling and Underground Works, 1995(5): 52-75. (in Chinese))

[7]尹海卿. 港珠澳大橋島隧工程設計施工關鍵技術[J]. 隧道建設, 2014, 34(1): 60-66. (YIN Haiqing. Key technologies applied in design and construction of artificial islands and immersed tunnel of Hong Kong-Zhuhai-Macao Bridge (HZMB) Project[J]. Tunnel Construction, 2014, 34(1): 60-66. (in Chinese))

[8]中交第一航務工程勘察設計院有限公司. 港口工程荷載規范: JTS 144-1—2010[S]. 北京: 人民交通出版社, 2010： 34-39. (CCCC First Harbor Consultants Co.,Ltd. Load code for harbour engineering: JTS 144-1—2010[S]. Beijing: China Communications Press, 2010： 34-39. (in Chinese))

Analysis and Application of Axial Line Rectification of Segment E4 of Honggu Tunnel in Nanchang

XING Yonghui1, ZHANG Yi2, LI Zhijun3

(1.ChinaRailwayTunnelSurvey&DesignInstituteCo.,Ltd.,Tianjin300133,China; 2.GuangzhouSalvageBureau,Guangzhou510260,Guangdong,China; 3.ErchuCo.,Ltd.ofChinaRailwayTunnelGroup,Sanhe065201,Hebei,China)

Nanchang Honggu Tunnel is a longest inland river tunnel in China. The immersed section of Honngu Tunnel is 1 329 m long and includes 12 segments. The axial line accuracy of segment installation is the key. The main influencing factors of tunnel segment installation accuracy are calculated, and the axial line deviation rectification of tunnel segment is carried out by using horizontal adjusting system. The comparison between measured data and theoretical calculation results shows that the above-mentioned axial line deviation rectification method is effective. The study results can provide reference for similar projects in the future.

immersed tunnel; segment sinking; segment installation; axial line rectification

2016-05-05;

2016-06-20

邢永輝(1978—)，男，河南浚縣人，2001年畢業于西南交通大學，鐵道與道路工程專業，本科，高級工程師，現從事地下工程設計工作。E-mail: skyhorse_xyh@163.com。

10.3973/j.issn.1672-741X.2016.09.011

U 455.46

B

1672-741X(2016)09-1101-05