風險管理在成本估算過程中的應用研究

王濤（上海電氣電站工程公司， 上海 200240）

風險管理在成本估算過程中的應用研究

A STUDY ON THE APPLICATION OF RISK MANAGEMENT IN COST ESTIMATION PROCESS

王濤（上海電氣電站工程公司， 上海 200240）

風險與不確定是有區別的，風險可以定義為產生不良后果的可能性，風險是必然發生的，事件發生的可能性無論是從主觀上還是客觀上都是可以估計的，而不確定是指事情不知道會否發生。在成本估算過程中，風險無法明確的給出大小，但我們可以借助現代工具給出一個風險的概率，然后用不同的風險態度做出決策。本文借助＠risk軟件，在成本估算過程中植入風險管理的理念，讓成本估算更加具有彈性。

成本估算；風險管理； ＠risk

0 引言

成本管理特別是編制建筑安裝工程的成本估算是一件非常困難的工作，因為建筑項目存在著風險和不確定性，特別是在項目前期，可利用的信息有限，無法準確的預估成本。傳統上，編制成本估算是通過確定的單一估算數字來進行的，這種做法的缺點是估算中沒有明確和系統的評估風險的方法，風險費用往往采用一個固定的數字。這種做法是不可取的，因為風險沒有被分開來識別比較，風險費用不是定高了就是定低了。此外，這種方法是效率低下和消極的，因為隨著工程的進行，部分風險已經被發現并且可以規避，因此這些已知的或可消除的風險費用應該加以調整，以便有更多的資金可用于未知的風險。

1 工程建設項目中的風險管理

風險是一個抽象的概念，簡單的講，風險可以定義為產生不良后果的可能性［1］。風險和不確定之間的區別很小，通常的區別是：在風險情況下，根據可參考的客觀信息，事件發生的可能性無論從客觀上還是主觀上都是可以估計的，而不確定是指一件事情不能知道是否會發生。John Raftery同樣指出風險是可以量化的而不確定卻不能［2］。

對建設項目成本估算而言，需要考慮四種風險：數量風險、單價風險、進度風險和綜合風險。綜合風險包括勞動率、承包商利潤以及稅金等的變化。

Flangan和Stevens認為簡單的風險管理系統包括三個步驟，分別是：識別和區分風險、分析風險、風險應對［3］。盡管很多作者從不同角度來解釋風險管理方法，但是所有方法的核心內容是一致的，這個核心內容包括：風險識別、風險測量、風險評估、風險處置、風險監控。

對風險的評估量化可以采用對所有風險因素的客觀信息和客觀概率分布來明確，比如人工單價的漲價風險因素，可以參考歷年來的人工費用、社會平均工資以及CPI來分析。當客觀信息不可用時，那么就要用到主觀概率分布，例如明天下雨的概率有的人認為是30%，有的人認為是70%，這就是主觀因素判斷。風險管理的目的不是給出精準的數據，而是要找出對判斷最有幫助的哪一個，因此，問題不在于輸入變量的真實分布，而在于每個變量的分布所表達的趨勢判斷。對主觀概率分布的評估方法，我們主要用到判斷、德爾菲法、頭腦風暴法等。

2 成本估算模型

通常成本計算模型可以分為兩類：確定型成本模型和概率型成本模型。

（a） 確定型成本模型預測成本的公式是：

［元素成本］=［元素數量］×［元素單價］

n個元素的總成本是：

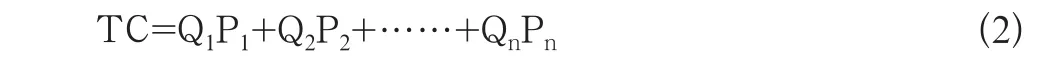
上述模型中的CQP都是固定的數字，他默認所有風險值都是固定的，計算的最終結果也是一個單一數字，這個單一的結果往往導致對真實成本的誤判或誤導，真實的成本不僅僅是一個平均值而是應該隨著時間和空間的推進而產生波動，因此，成本不是固定不變的。

（b） 概率型成本模型預測成本的公式是：

［元素成本概率區間］=［元素數量概率區間］×［元素單價概率區間］+［綜合風險因素成本］

n個元素的總成本是：

在這種模型中，數量和單價均不是固定的，而是一個概率范圍，概率分布來自大量的之前項目成本數據，這樣一來總成本也會是一個概率分布。蒙特卡洛模擬法經常被用來進行概率分布的測算。蒙特卡洛模擬過程如圖1所示：

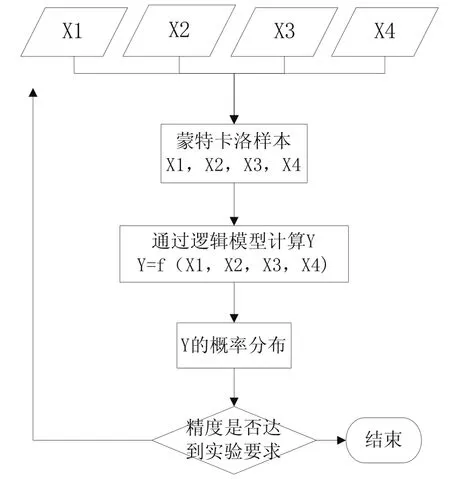
圖1 蒙特卡洛模擬

3 風險管理在成本估算過程中的應用步驟

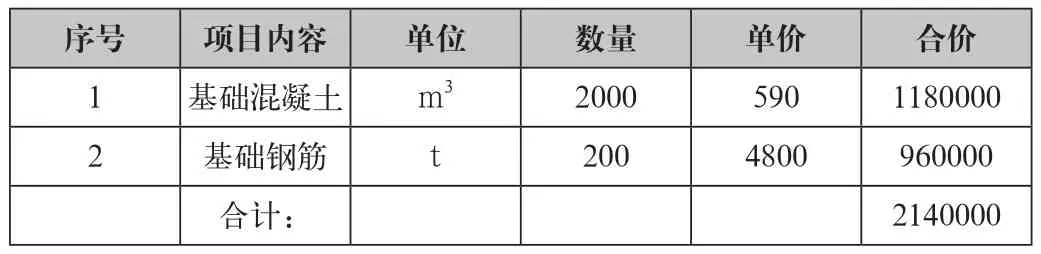
表1 傳統成本估算

表1顯示了傳統上對成本的計算方法，從表中可以看到計算成本的幾個參數：數量、單價、合價。這幾個參數都是固定值，也就默認了數量和單價均不作變動，計算的最終成本也不會變。但我們知道事物絕對不會是永恒不變的，隨著時間的推移、周圍環境的改變以及市場情況的變化，數量和單價都有可能有調整，由此看來這種成本方式存在很大的問題，那么我們就利用概率估算方法將風險管理貫穿至估算過程中去，基本分為9個步驟。

步驟1：確定基本成本估算

基本的成本估算模型首先采用確定型估算模型，既公式（2），但需注意的是表1所示的單價為綜合單價，我們需要做單價分析進行更加精確的成本估算，單價分析我們利用電力建設工程定額的數據來完成，基本的估算元素有三個，分別是：人工、機械和材料，除此之外，我們還要考慮風險費用。元素單價的組成公式為：

［元素單價］=［人工價格］+［材料價格］+［機械價格］+［風險費用］=人工數×人工單價+材料數量×材料單價+機械數量×機械單價+風險費用

步驟2：風險識別

從成本估算公式中我們可以看出，影響成本的風險主要包括數量風險、價格風險、時間風險、其他風險及各風險因素之間的相關性。我們將所有風險因素列表，如表2所示：

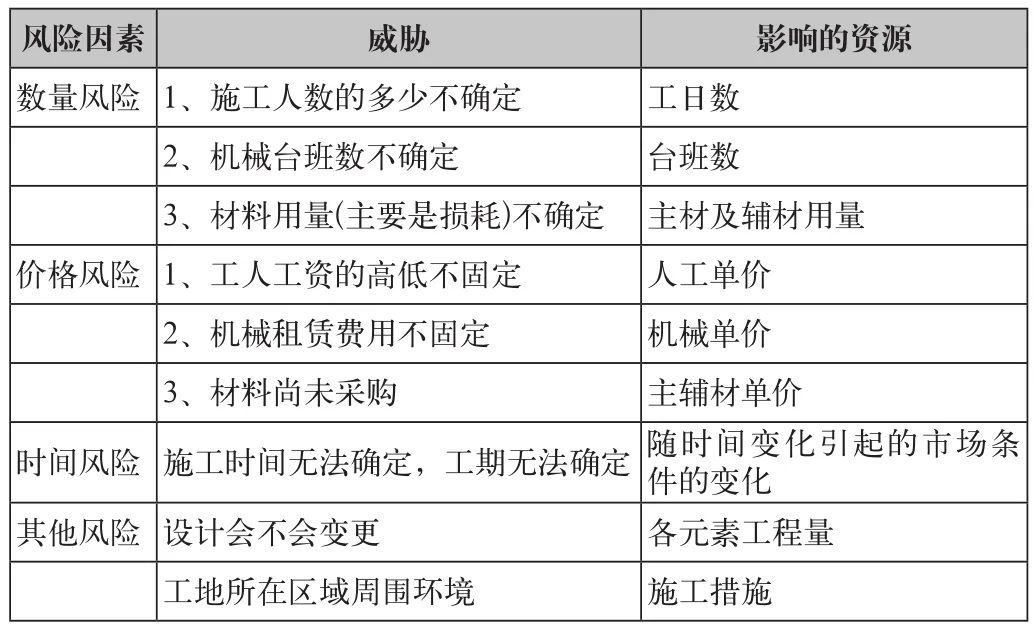
表2 風險列表

步驟3：風險測量

風險測量是指確定所有潛在風險因素的影響大小，有時候由于缺少可用的信息，需要利用主觀判斷。表3為根據歷史數據、可查詢公用數據及歷史經驗做出的風險測量。在確定每個風險因素的概率分布類型時，可能會用到正態分布、β分布等，但在工程建設項目中最常用到的概率分布類型是三角分布（如圖2所示），它基于兩個假設：第一個假設是對變量極端值的概率賦值較低，如圖2中的a與c，對變量最可能值的概率賦值較高，如圖2中的b；第二個假設是變量的概率成線性變化。

表3 風險測量

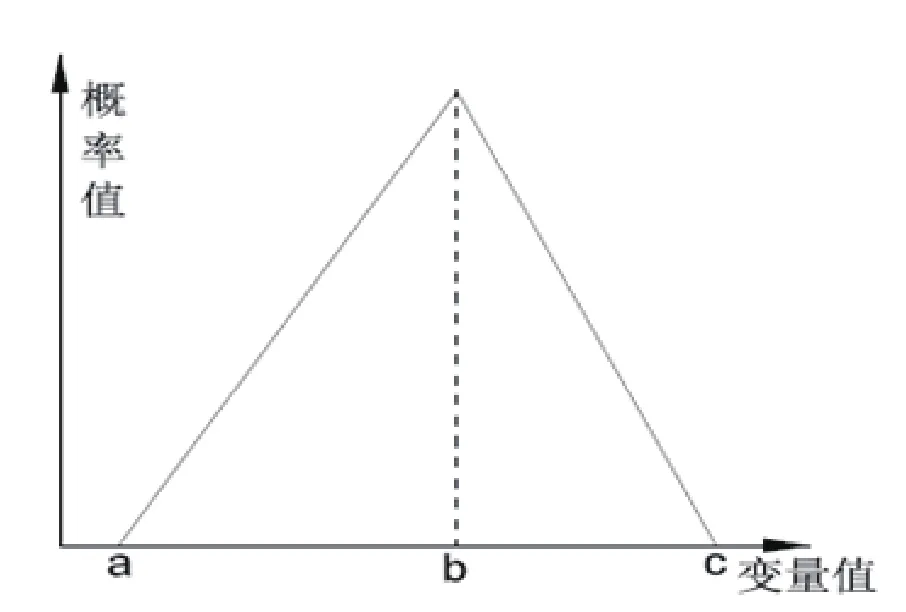
圖2 三角概率分布

步驟4：建立成本模型

圖3所示是本例的成本估算模型，我們利用EXCEL以及嵌入式軟件＠RISK來完成建模。從圖中我們可以看到有15個輸入值和5個輸出值，輸入值按照表3所示的風險因素及概率分布輸入，其中CPI風險根據2015年12個月的全國CPI數據利用＠RISK軟件分析得出；輸出值公式分別是：

基礎砼單價［輸出1］=∑16（輸入i×輸入j）×（1+CPI）n基礎鋼筋單價［輸出2］=∑712（輸入i×輸入j）×（1+CPI）n

基礎砼合價［輸出3］=輸入14×輸出1

基礎鋼筋合價［輸出4］=輸入15×輸出2

自主學習作為一種以人本主義心理學和認知心理學為基礎的現代學習理念，提倡從以教師為中心的教育向以學生為中心的教育轉變[3]。自主學習強調培育學生強烈的學習動機和濃厚的學習興趣，從而進行能動的學習，即主動地自覺自愿地學習，而不是被動地或不情愿地學習。為此，建設豐富的網絡教學資源，如精品資源共享課、吉醫在線學堂課程等，并以吉醫在線學堂為依托，開展組織學與胚胎學翻轉課堂教學。

總成本［輸出5］=輸出3+輸出4

其中n在方案1時取1值，在方案2時取0值。

各風險因素之間存在相關性，例如隨著CPI的上漲，人工單價及材料單價也會上漲，這種概率是相輔相成的，在模型中我們要設定相關矩陣，如圖4所示。

步驟5：風險評估

我們利用＠RISK軟件的模擬功能，設置方案1和方案2分別模擬1000次，得出結果如圖5所示。從圖中我們可以看出方案1：總成本的最小值、平均值和最大值分別是1958524、2128386、2335905，其中總成本小于2254155的概率為95%；方案2：總成本的最小值、平均值和最大值分別是1980838、2151559、2359448，其中總成本小于2276933的概率為95%。

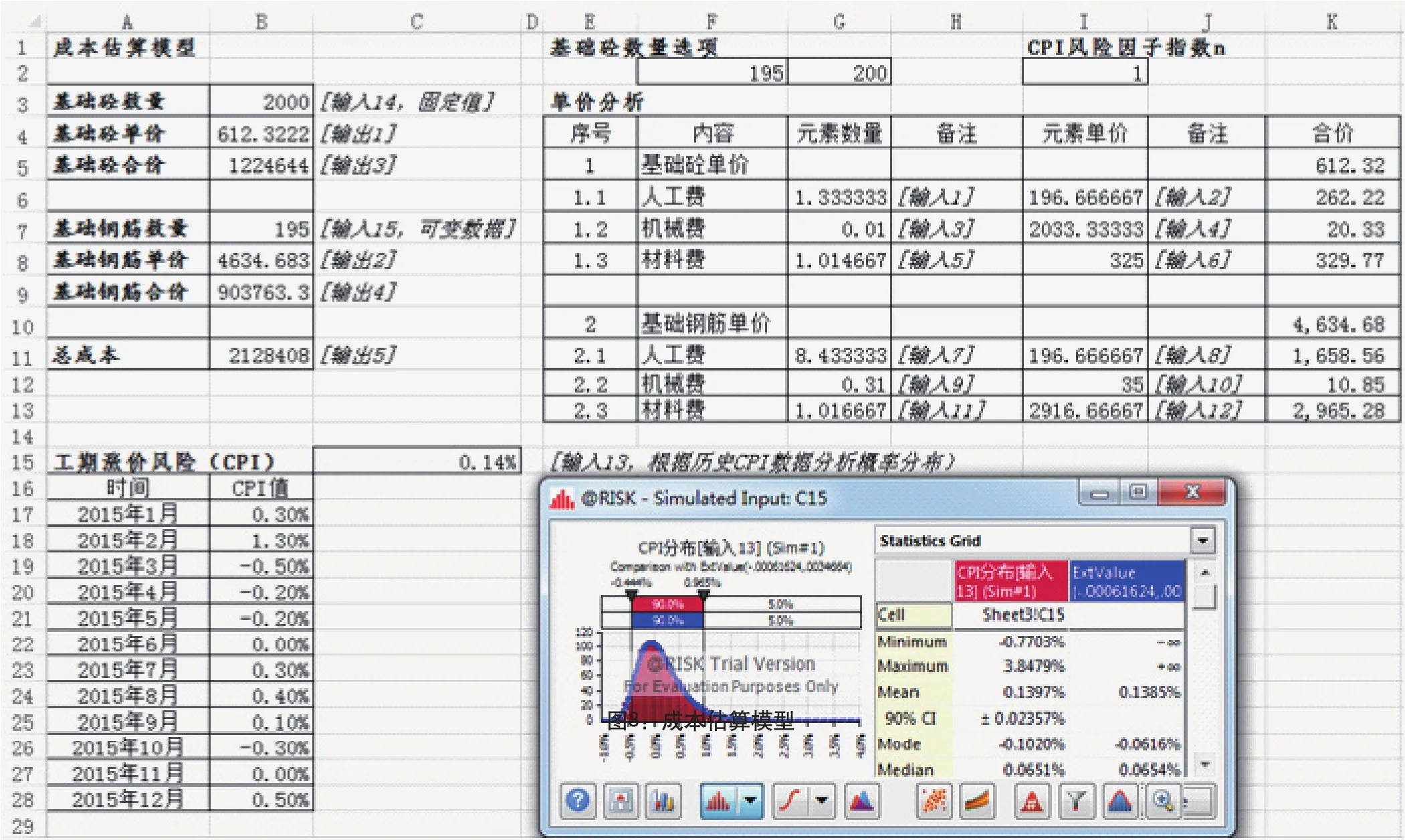
圖3 成本估算模型

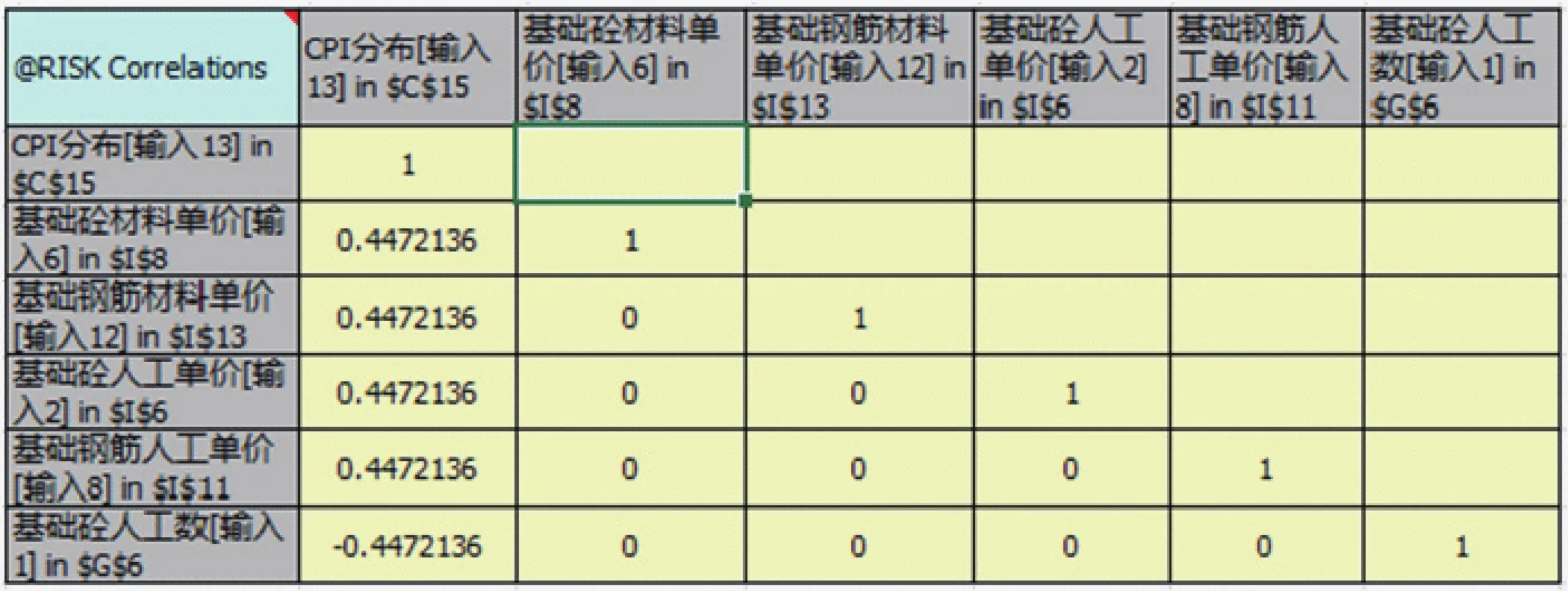
圖4 相關矩陣

步驟6：風險對策

步驟7：風險監控及控制

這一步驟是指連續不斷的審查項目過程并作出正確的行動去完成項目目標。隨著時間的推移，部分風險已經被發現并可以消除，這些已知的或可以消除的風險應對及時更新，例如本例中存在方案1和方案2，隨著時間的推進，方案確定后工期也就確定，CPI風險指數也可以確定，這些風險因素確定后我們的成本估算就會更加準確。

步驟8：更新并審查風險

步驟2制定的風險列表在不同的階段需要進行更新并且需要用到不同的成本模型，步驟3到步驟8需要反復執行直到項目結束。

步驟9：項目結束

項目結束后，項目成本信息需要反饋到歷史數據庫中以備將來之需。

4 結語

成本估算是一件困難的工作，在項目前期缺少可用信息的情況下更是如此，過程中存在著大量的風險和不確定，這些風險和不確定對成本的影響很大，但是傳統的估算方法中沒有明確的風險評估。我們通過將風險管理的全過程植入成本估算過程中，并利用現代工具進行模擬數據，得出成本的概率區間，并用一定的風險態度去應對風險，這樣就會使成本估算更加具有彈性，降低成本超支的風險，具有實際使用價值。

［1］郭婧娟，劉伊生.工程造價管理［M］.北京：清華大學出版社，北京交通大學出版社，2005，P188.

［2］JOHN RAFTERY.，Risk Analysis in Projects Management，P3-23.

［3］FLANGAN & STEVENS.，Risk Analysis，Quantity Surveying Techniques New Directions，BSP Professional Books，Oxford，1990，P121-138.