隨機波動率下的障礙期權定價

摘要： 針對障礙期權的定價問題，建立具有隨機波動率和有交易費用的障礙期權的定價模型。在無套利定價原則和風險中性定價原則下推導出期權價格方程。采用有限差分法求解該方程，獲得了期權價格的數值解。并通過數值試驗的方法分析和討論了模型中部分參數對期權價格的影響。

Abstract： In view of the problem of pricing barrier option， the model is established under the condition of stochastic volatility and transaction cost. Under the principle of no arbitrage pricing and the principle of risk neutral pricing， the price equation of option is derived. The finite difference method for solving the equation is given， and the numerical solution of the option price is obtained. And the influence of some parameters on the option price is analyzed and discussed by numerical experiments.

關鍵詞： 隨機波動率；自由邊界；有限差分；美式期權

Key words： stochastic volatility；free boundary；finite difference；American options

中圖分類號：F224；F830.7 文獻標識碼：A 文章編號：1006-4311（2016）07-0045-03

0 引言

期權是市場上最受歡迎的金融衍生工具之一，具有良好的規避風險的功能。期權的定價問題已逐漸成為金融數學領域研究的熱點問題之一，近年來已取得一些研究成果。文獻[1]利用C-N格式的有限差分方法求解障礙期權價格滿足的偏微分方程，得到了期權價格。文獻[2]給出了股指期貨障礙期權價值的B-S公式，并討論了解法。文獻[3]采用一種高階隱式有限差分方法用于求解障礙期權定價問題。文獻[4]分別建立了離散型和連續型上漲出局期權的定價模型，并給出求解該模型的線性逼近方法。文獻[5]通過求解微分方程獲得下降敲出期權和上升敲出期權的解析定價公式。文獻[6]在跳躍擴散模型下使用總體最小二乘蒙特卡羅模擬方法對美式障礙期權定價問題進行了研究。文獻[7]證明了指數障礙期權的拋物型方程問題存在唯一解.目前，對障礙期權定價的研究大多都是在波動率為常數的條件下進行的。然而，在實際金融市場中標的股票的波動率會隨時間發生變化。鑒于此，本文考慮更符合市場規律的障礙期權定價問題，在文獻[4]和[7]的基礎上，建立基于隨機波動率的障礙期權定價模型，并給出數值解法。

1 隨機波動率模型

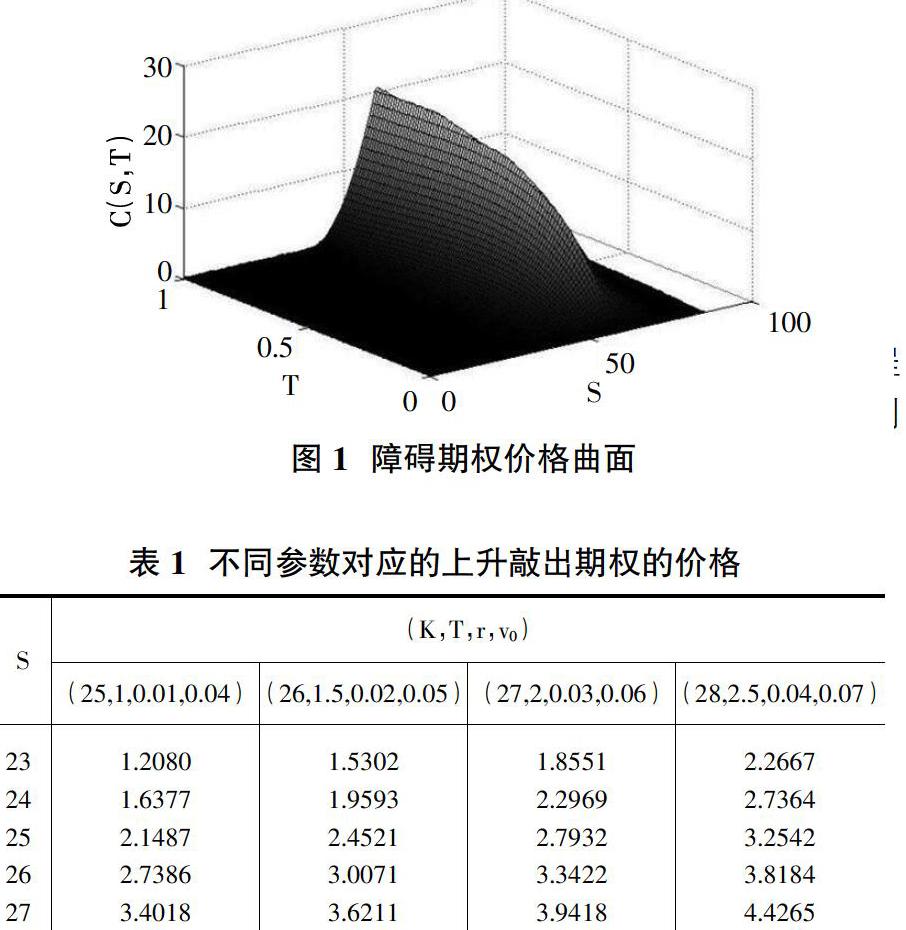
4 數值試驗

5 結束語

本文考慮帶有Heston隨機波動率模型的障礙期權的定價問題，給出了求解期權定價方程的數值方法，獲得了期權價格的數值解，并對期權價格的影響因素做了討論和分析。然而，針對基于隨機波動率的期權定價的研究不限于此，如多資產障礙期權的定價問題等仍有待研究。

參考文獻：

[1]M. Yousuf. Efficient smoothing of Crank-Nicolson method for pricing barrier options under stochastic volatility [J]. Proceedings in Applied Mathematics and Mechanics，2008，7：1101-1102.

[2]徐騰飛，曹小龍，胡云姣.離散障礙期權定價的蒙特卡羅模擬[J].北京化工大學學報（自然科學版），2013，40（3）：123-127.

[3]J. C. Ndogmo， D. B. Ntwiga. High-order accurate implicit methods for barrier option pricing [J]. Applied Mathematics and Computation，2011，218：2210-2224.

[4]Carl Chiarella，Boda Kang，et al. The evaluation of barrier option prices under stochastic volatility [J]. Computers and Mathematics with Applications，2012，64：2034-2048.

[5]孫玉東，師義民，吳敏.參數依賴股票價格情形下的障礙期權定價[J].數學物理學報，2013，33（5）：912-925.

[6]張利花，張衛國，許文坤.美式障礙期權定價的總體最小二乘模擬蒙特卡羅模擬方法[J].數理統計與管理，2013，32（5）：923-929.

[7]Dong Yan. Existence and Uniqueness of parabolic problem arising in exponential double barrier option [J].Journal of quantitative economics，2013，30（1）：82-88.

[8]S. Heston. A closed-form solution for options with stochastic volatility with applications to bond and currency options [J]. Review of Financial Studies，1993，6（2）：327-343.

[9]李建輝，賀興時，楊睿通.有交易費用和紅利的美式期權的緊差分逼近[J].西安工程大學學報，2012，26（5）：667-671.

[10]Black，F. and M. Scholes. The Valuation of Option Contracts and a Test of Market Efficiency [J]. Journal of Finance，1972，27：399-417.

[11]Arun Chockalingam，Kumar Muthura-man. An approximate moving boundary method for American option pricing [J]. European Journal of Operational Research，2015，240（2）：431-438.

[12]K. J. int Hout S. Foulon. ADI finite difference schemes for option pricing in the Hestonmodel with correlation，Int. J. Number. Anal. Mod，2010，7：303-320.