基于迭代積分卡爾曼PHD濾波多目標(biāo)跟蹤

穆祥強(qiáng)，王朝英，危璋，孔云波

(空軍工程大學(xué) 信息與導(dǎo)航學(xué)院，陜西 西安　710011)

?

基于迭代積分卡爾曼PHD濾波多目標(biāo)跟蹤

穆祥強(qiáng)，王朝英，危璋，孔云波

(空軍工程大學(xué) 信息與導(dǎo)航學(xué)院，陜西 西安710011)

在多目標(biāo)跟蹤環(huán)境下，通過對數(shù)值積分卡爾曼概率假設(shè)密度濾波器(QK-PHD)的誤差分析，提出一種迭代QK-PHD算法。該算法基本思想是將一步預(yù)測作為第1次迭代的初始值，通過量測更新得到狀態(tài)估計，然后將此狀態(tài)估計作為下一步迭代的初始均值和方差。通過多次迭代后濾波輸出精度更高方差更小。Matlab仿真結(jié)果表明，在不明顯增加計算時間的基礎(chǔ)上，迭代QK-PHD比QK-PHD的跟蹤效果更加明顯，濾波輸出精度更高。

迭代；多目標(biāo)跟蹤；狀態(tài)估計；數(shù)值積分；卡爾曼濾波；概率假設(shè)密度濾波

0　引言

非線性濾波問題廣泛存在于導(dǎo)航、目標(biāo)跟蹤、數(shù)字通信等領(lǐng)域，其基本任務(wù)都是從當(dāng)前時刻目標(biāo)狀態(tài)估計和量測去估計出下一時刻的目標(biāo)狀態(tài)。在多目標(biāo)環(huán)境下，目標(biāo)的新生、衍生、合并導(dǎo)致目標(biāo)個數(shù)動態(tài)變化，而且在觀測過程中會引入大量的噪聲，這些噪聲影響著目標(biāo)的濾波精度。Mahler[1]根據(jù)有限集[2-4]提出概率假設(shè)密度濾波器(probability hypothesis density，PHD)。該方法不需要數(shù)據(jù)關(guān)聯(lián)從而得到廣泛應(yīng)用。

當(dāng)目標(biāo)的運(yùn)動模型為非線性高斯情況時，為了更加精確地跟蹤目標(biāo)，需要采用非線性濾波。Vo等人分別提出了擴(kuò)展卡爾曼PHD(extended Kalman filter PHD,EKF-PHD)和無跡卡爾曼PHD(unscented Kalman filter PHD,UKF-PHD)。但是擴(kuò)展卡爾曼濾波是展開泰勒級數(shù)來線性化模型，當(dāng)模型非線性化程度較大時其濾波誤差比較大。迭代擴(kuò)展卡爾曼濾波(iterated EKF，IEKF)[5]是基于量測信息來糾正非線性觀測函數(shù)的泰勒級數(shù)展開使之重新線性化，從而減小濾波的總體誤差。無跡卡爾曼[6-9](UKF)濾波受尺度參數(shù)的影響較大，使得協(xié)方差矩陣非正定，從而影響系統(tǒng)穩(wěn)定。文獻(xiàn)[10]提出了數(shù)值積分卡爾曼概率假設(shè)密度濾波算法，這個方法相對于擴(kuò)展卡爾曼PHD和無跡卡爾曼PHD在強(qiáng)非線性情況下具有更好的精度和跟蹤效果。文獻(xiàn)[11]將迭代理論與容積卡爾曼相結(jié)合使得濾波算法精度更高，本文在對此文獻(xiàn)深入的研究之后將Gauss-Newton[12]的迭代理論與QKF-PHD相結(jié)合提出了迭代數(shù)值卡爾曼概率假設(shè)密度濾波方法。在量測過程中通過迭代方法充分利用新的量測對目標(biāo)狀態(tài)的更新，降低了非線性的影響提高跟蹤精確度。仿真結(jié)果表明，基于迭代QKF-PHD相比于QKF-PHD跟蹤精度更高，更加穩(wěn)定。

1　概率假設(shè)密度算法(PHD)

傳統(tǒng)的跟蹤算法如概率數(shù)據(jù)關(guān)聯(lián)等算法都是通過對量測進(jìn)行分配，將多目標(biāo)問題轉(zhuǎn)化為并行的單目標(biāo)跟蹤處理問題，這類算法的核心問題都是數(shù)據(jù)關(guān)聯(lián)。但是當(dāng)目標(biāo)數(shù)過多時就會出現(xiàn)計算量指數(shù)增長、組合爆炸問題。概率假設(shè)密度基于有限集，利用一階統(tǒng)計距近似方法對目標(biāo)后驗概率函數(shù)求集合積分運(yùn)算，避免了直接計算完全后驗概率密度[13]。因此避免了傳統(tǒng)方法需要的數(shù)據(jù)關(guān)聯(lián)步驟，因此得到廣泛應(yīng)用。

假設(shè)用Dk|k和Dk|k-1分別表示pk(Xk|Z1:k)和pk|k-1(Xk|Z1:k-1)的PHD其遞推過程為

Dk|k-1(xk|Z1:k-1)=γk(xk)+

fk|k-1(xk|xk-1)]*Dk-1|k-1(xk-1|Z1:k-1)dxk-1，

(1)

Dk|k(xk|Z1:k)=(1-PD(xk))Dk|k-1(xk|Z1:k-1)+

(2)

式中：D(·)表示目標(biāo)強(qiáng)度；γk(xk)表示新生目標(biāo)強(qiáng)度；βk|k-1(xk|xk-1)為前一時刻衍生目標(biāo)強(qiáng)度；fk|k-1(xk|xk-1)為目標(biāo)轉(zhuǎn)移函數(shù)；ek|k-1(xk-1)為目標(biāo)存活概率；PD(xk)為目標(biāo)檢測概率；φk,z(xk)=PD(xk)gk|k(z|xk)為目標(biāo)似然函數(shù);gk|k(z|xk)為單目標(biāo)似然函數(shù);Dk(z)=κk(z)+Ck(z)為量測的強(qiáng)度;κk(z)為雜波

Ck(z)=∫φk,z(xk)Dk|k-1(xk|Z1:k-1)dx.

2　基于迭代QKF-PHD濾波算法

2.1QKF-PHD濾波算法

非線性系統(tǒng)為

(3)

式中：xk∈Rm和zk∈Rm分別為狀態(tài)向量和量測向量；wk-1和vk分別為系統(tǒng)噪聲和量測噪聲，服從零均值方差為Qk-1，Rk的高斯分布；f(·)和h(·)分別為狀態(tài)轉(zhuǎn)移函數(shù)和量測方程。

假設(shè)隨機(jī)變量x，其概率密度分布服從標(biāo)準(zhǔn)的高斯分布x～N(0,1)，對于任意的關(guān)于x的函數(shù)g(x)，其積分為

(4)

式中：ξj為積分點；ωj為權(quán)值；m為積分點個數(shù)，使用文獻(xiàn)[14]提出了一種計算積分點的方法。構(gòu)造一個三角對稱矩陣J,其對角線的元素全部為0，其他元素為

(5)

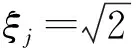
QKF-PHD的算法流程為：

設(shè)k-1時刻的后驗概率假設(shè)密度的高斯形式表示為

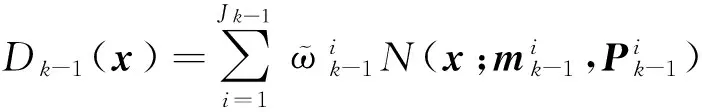
(1) 時間預(yù)測

1) 矩陣分解

(6)

2) 求取積分點

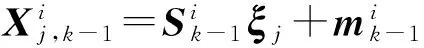
(7)

3) 傳播積分點

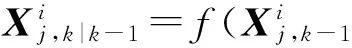
(8)

4) 狀態(tài)一步預(yù)測與協(xié)方差

(9)

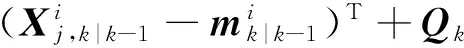
(10)

(11)

(2) 量測更新

1) 矩陣分解

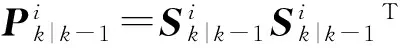
(12)

2) 求取積分點

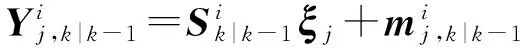
(13)

3) 傳播積分點

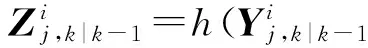
(14)

4) 量測預(yù)測以及協(xié)方差

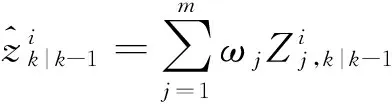
(15)

(16)

5) 互協(xié)方差

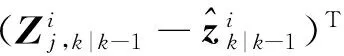
(17)

6) 濾波增益

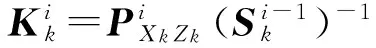
(18)

7) 計算量測更新與協(xié)方差

(19)

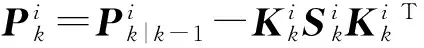
(20)

QKF-PHD的權(quán)值更新為

(21)

后驗PHD為

Dk(x)=(1-Pd(x))Dk|k-1(x)+

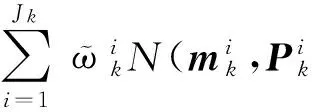
(22)

2.2迭代QKF-PHD(IQKF-PHD)算法的實現(xiàn)

因為在QKF的濾波算法中一步預(yù)測難免會出現(xiàn)誤差，通過迭代不斷地對量測新息與方差進(jìn)行修正就可以降低誤差，IQKF-PHD的時間預(yù)測方程仍如QKF-PHD，但是其量測步驟更新需改變。

IQKF-PHD算法的步驟如下：

時間更新

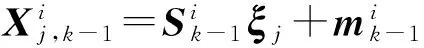
(23)

(24)

狀態(tài)預(yù)測與協(xié)方差為

(25)

(26)

量測更新

首先計算第t次迭代的積分點與傳遞值為

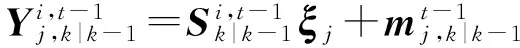
(27)

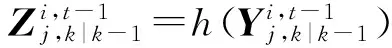
(28)

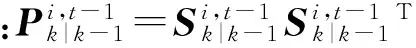
計算量測預(yù)測、新息協(xié)方差和協(xié)方差分別為

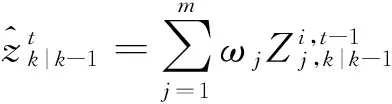
(29)

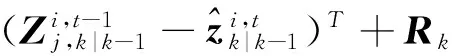
(30)

(31)

其次計算第i次迭代的濾波增益、狀態(tài)估計以及協(xié)方差

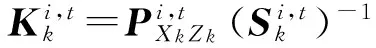
(32)

(33)

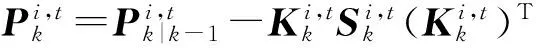
(34)

最后迭代的終止條件。終止條件為

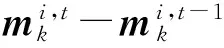
設(shè)迭代的終止的迭代次數(shù)為N，則k時刻的狀態(tài)估計與方差為

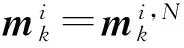
(35)

(36)

3　仿真與分析

通過試驗，對比本文提出的算法與QKF-PHD，IEKF-PHD算法性能對比分析，證明本文提出算法的有效性。

(1) 試驗仿真環(huán)境

設(shè)初始時刻存在2個目標(biāo)，初始狀態(tài)分別為(1 000,100,-1 000,-100)和(1 000,100,-3 000,100)，第3個目標(biāo)出現(xiàn)時刻為20 s。目標(biāo)做以ω=0.05 rad/s作圓周運(yùn)動，目標(biāo)1與目標(biāo)2運(yùn)動軌跡有交叉，假設(shè)目標(biāo)存活概率為1，檢驗概率為0.95，觀測站位于(0，0)。過程噪聲wk-1為高斯白噪聲，方差為10 m2/s2。vk為量測噪聲其方差角誤差為0.01 rad2，距離誤差為100 m2。蒙特卡羅仿真次數(shù)為35次，選取積分點為2個。采用評價指標(biāo)為最優(yōu)子模型分配(optimal subpattern assignment，OSPA) 距離，在這次仿真中對勢估計的懲罰程度和對狀態(tài)估計的懲罰程度都取值為1。

目標(biāo)跟蹤模型如下

Xk=FXk-1+wk-1,

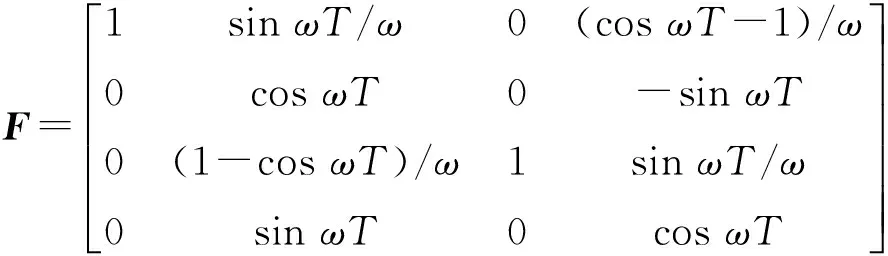
(2) 仿真結(jié)果分析

仿真結(jié)果如圖1～5所示。

圖1　目標(biāo)運(yùn)動軌跡Fig.1　Track of motional target

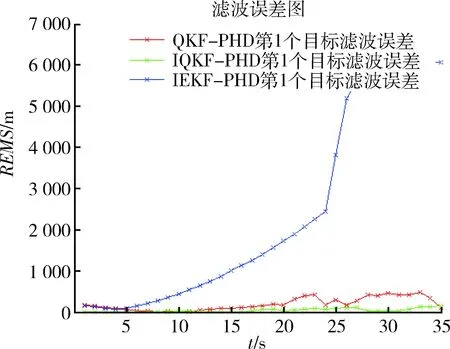
圖2　第1個目標(biāo)OSPA距離Fig.2　First target OSPA distance

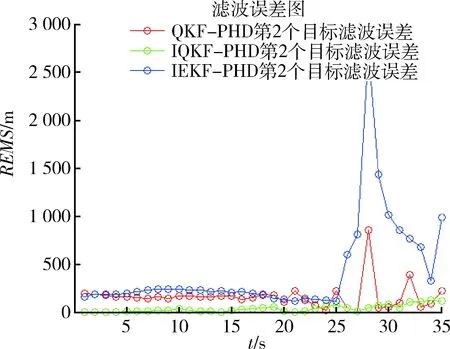
圖3　第2個目標(biāo)OSPA距離Fig.3　Second target OSPA distance

圖4　第3個目標(biāo)OSPA距離Fig.4　Third target OSPA distance

圖5　目標(biāo)總的OSPA距離Fig.5　Three-target OSPA distance

圖1是目標(biāo)的運(yùn)動軌跡，其軌跡為曲線。在t=20 s時候出現(xiàn)第3個目標(biāo)，也就是產(chǎn)生新的目標(biāo)。從圖2中可以看出IEKF-PHD算法在t=23～24 s時候還能跟蹤上，但是之后算法跟蹤開始發(fā)散無法跟蹤目標(biāo)運(yùn)動。其他2種算法QKF-PHD和IQKF-PHD跟蹤上了目標(biāo)運(yùn)動而且效果比IEKF-PHD效果要好得多。從后面2種算法的性能比較可以看出，IQKF-PHD算法的跟蹤精度更高，跟蹤效果最好。從圖3～5中可以看出QKF-PHD與IQKF-PHD算法在跟蹤目標(biāo)1時后一種算法更加平穩(wěn)，對每一個目標(biāo)的跟蹤其OSPA距離都是最低的。當(dāng)t=27 s時刻目標(biāo)3的運(yùn)動軌跡與目標(biāo)2的運(yùn)動軌跡交叉，從圖5可以看出其他2個算法在此時刻都出現(xiàn)了誤差增大，而本文算法則沒有。由此可得，本文提出的IQKF-PHD散發(fā)跟蹤精度要明顯優(yōu)于其他2個跟蹤算法，體現(xiàn)了該算法的優(yōu)越性。

4　結(jié)束語

本文結(jié)合了迭代思想與QKF-PHD算法的優(yōu)點提出了迭代QKF-PHD算法。該算法利用迭代思想對量測更新步驟進(jìn)行迭代，充分利用了新的量測對目標(biāo)狀態(tài)的更新，提高了數(shù)值卡爾曼概率假設(shè)密度算法對目標(biāo)跟蹤精度。仿真結(jié)果表明，本文提出的算法相對與其他2種算法具有更好的跟蹤效果，其穩(wěn)定性與魯棒性得到明顯的提升。

[1]MAHLER R P S.Multitarget Bayes Filtering via First-Order Multitarget Moments[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1152-1178

[2]楊峰,王永齊,梁彥.基于概率假設(shè)密度濾波方法的多目標(biāo)跟蹤技術(shù)綜述[J].自動化學(xué)報,2013,39(11):1944-1956.

YANG Feng, WANG Yong-qi, LIANG Yan.A Suivey of PHD Filter Based Multi-Target tracking[J]. Acta Automatic Sinica, 2013,39(11):1944-1956.

[3]鄒其兵.多伯努利濾波器及其在檢測前跟蹤中的應(yīng)用[D].西安：西安電子科技大學(xué),2012.

ZOU Qi-bing. Study of Multi-Bernoulli Filter and Its Applications to Track Before Detection[D]. Xi′an:Xidian University,2012.

[4]張鶴冰.概率假設(shè)密度濾波算法及其在多目標(biāo)跟蹤中的應(yīng)用[D].哈爾濱：哈爾濱工程大學(xué),2012.

ZHANG He-bing.Probability Hypothesis Density Filter Algorithm and Its Application in Multi-Targets Tracking[D].Harbin:Harbin Engineering University,2012.

[5]BELL B M，CATHEY F W. The Iterated Kalman Filter Update as a Gauss-Newton Method [J]. IEEE Trans on Automatic Control, 1993, 38(2): 294-297.

[6]JULIER S J, UHLMANN J K, DURRANT-WHYTE H F.A New Method for the Nonlinear Transformation of Means and Covariance in Filters and Estimators [J]. IEEE. Transactions on Automatic Control , 2000,45(3):477-482.

[7]JULIER S J,UHLMANN J K. A New Extension of the Kalman Filter to Nonlinear System [C]∥SPIE,1997:3068,182-193.

[8]伊建君,張建秋,林青.Unsecented卡爾曼濾波-卡爾曼濾波算法[J].系統(tǒng)工程與電子技術(shù)，2008,30(4):617-620.

YI Jian-jun,ZHANG Jian-qiu,LIN Qing.Filter Algorithm Based on Unsented Kalman Filter [J]. Systems Engineering and Electronics,2008,30(4):617-620.

[9]JULIER S J. The Spherical Simplex Unscented Transformation[C]∥ Proc. Am. Contr. Conf. Denver, Colorado, 2003: 2430-2434.

[10]陳里銘, 陳喆, 殷福亮,等. 基于數(shù)值積分卡爾曼概率假設(shè)密度濾波的多說話人的跟蹤方法[J]. 信號處理, 2012, 25(10): 1209-1214.

CHEN Li-ming, CHEN Zhe, YIN Fu-liang, et al. Quadrature Kalman PHD Filter for Multiple Speakers Tracking[J].Signal Processing,2012,25(10):1209-1214.

[11]穆靜, 蔡遠(yuǎn)利. 迭代容積卡爾曼濾波算法及其應(yīng)用[J]. 系統(tǒng)工程與電子技術(shù)，2011, 33(7): 1454-1457.

MU Jing,CAI Yuan-li. Interated Cubature Kalman Filter and Its Application[J].Systems Engineering and Electronics,2011,33(7):1454-1457.

[12]武良丹,賀西平,張小鳳.超聲回波參數(shù)的高斯與牛頓迭代計算[J].陜西師范大學(xué)學(xué)報,2006,34(3):56-58.

WU Liang-dan,HE Xi-ping,ZHANG Xiao-feng.The Calculation of Ultrasonic Echo Parameter by Gauss-Newton Iterative Method[J].Journal of Shaanxi Normal University,2006,34(3):56-58.

[13]王曉, 韓崇昭, 連峰. 基于隨機(jī)有限集的目標(biāo)跟蹤方法研究及最新進(jìn)展[J]. 工程數(shù)學(xué)學(xué)報, 2012, 29(4): 568-578.

WANG Xiao,HAN Chong-zhao,LIAN Feng.Survey of Target Tracking Based on Random Finite Set[J]. Chinese Journal of Engineering Mathematics, 2012,29(4):568-578.

[14]巫春玲, 韓崇昭.平方根求積分卡爾曼濾波器[J].電子學(xué)報, 2009,37(5):987-992.

WU Chun-ling,HAN Chong-zhao.Square Root Quadrature Kalman Filter[J]. Acta Electronica Sinica,2009,37(5):987-992.

[15]劉玉磊,馮新喜,鹿傳國,等.帶漸消因子的Quandrature卡爾曼濾波[J].宇航學(xué)報,2013,37(8):1328-1338.

LIU Yu-lei, FENG Xin-xi,LU Chuan-guo,et al.A Fading Quadrature Kalman Filter for Nonlinear Systems[J]. Journal of Astronautics,2013,37(8):1328-1338.

Probability Hypothesis Density Filter Algorithm Based on Iterated Quadrature Kalman Filter

MU Xiang-qiang，WANG Zhao-ying，WEI Zhang，KONG Yun-bo

(AFEU,Infornmation and Navigation College,Shaanxi Xi’an 710077,China)

Under the condition of multi-target tracking, by analyzing the error of quadrature Kalman probability hypothesis density filter (QK-PHD), the iterated QKF algorithm is proposed. The IQKF-PHD is used to re-estimate the one-step state and measurement predictions by virtue of the measurement updated state variable, and then the mean and variance of state variable are estimated. After several iterations, the outputs of IQKF-PHD have higher accuracy and less variance. Matlab simulation results demonstrate that the tracking accuracy and the outputs of IQKF-PHD are superior to those of QKF-PHD.

iterated;multitarget tracking;state variable; quadrature;Kalman filter; probability hypothesis density(PHD)

2015-06-19；

2015-09-21

陜西省自然科學(xué)基金(2011JM.8023)

穆祥強(qiáng)(1989-)，男，江蘇宿遷人。碩士生，研究方向為多目標(biāo)跟蹤。

通信地址：201600上海市松江區(qū)九亭鎮(zhèn)王家?guī)炻?75樓2號1404室E-mail：1097516121@qq.com

10.3969/j.issn.1009-086x.2016.04.016

TN713；TP391.9

A

1009-086X(2016)-04-0095-06