多波束測深誤差源對測點位置歸算影響研究
張志偉,暴景陽,肖付民
(海軍大連艦艇學院 海洋測繪系,遼寧 大連 116018)
多波束測深誤差源對測點位置歸算影響研究
張志偉,暴景陽,肖付民
(海軍大連艦艇學院海洋測繪系,遼寧大連116018)
針對Rob Hare提出的多波束測點位置歸算精度估計模型的不足,建立了顧及各項改正數之間相關性的改進模型。在多波束測點位置歸算模型的基礎上,分析了影響測點位置歸算的各項誤差來源,推導了各誤差源對測點位置歸算精度估計的影響量,結合算例,分別利用兩種模型計算了各誤差源對測點位置歸算精度的影響量級,繪制了各誤差源的誤差曲線圖與總位置誤差曲線圖,通過對計算結果的分析比較,得出了兩種模型在評估多波束測點位置歸算精度時存在的差異,由于顧及到改正數間的相關性,認為改進模型更加科學合理。
多波束測深系統;位置歸算;精度估計;改進模型;誤差曲線
由于多波束測深系統具有全覆蓋、高精度、高密度和高效率的特點[1],已成為當今海底地形測量的重要手段;但同時由于海洋測量的動態性、多波束測深系統本身具有的復雜的結構以及眾多的輔助設備,導致影響多波束測深誤差源很多[2-7]。精密多波束海底地形測量需要進行有效的深度改正和精確的位置歸算,就測點位置歸算而言,主要包括動態偏心改正、動態位置傳算以及動態時延改正[8]。
本文將對多波束測點位置歸算過程中影響測點位置的誤差源進行分析,對Rob Hare[9]提出的位置歸算誤差模型進行改進,分別利用原模型和改進模型計算各誤差源對測點位置歸算精度估計的影響量以及總的測點位置精度估值,并通過算例對原模型及改進模型進行比對分析。
1 測點位置歸算模型
首先建立載體坐標系(x,y,z)和站心大地坐標系(X,Y,Z),兩坐標系原點重合,為方便后文計算,將換能器中心作為坐標系原點,橫搖角為R、縱搖角為P、航向角為α,在此基礎上將分別建立測點位置歸算的動態偏心改正模型、動態位置傳算模型以及動態時延改正模型[9-12]。
假設定位設備在載體固聯坐標系中的坐標為(xa,ya,za),則可得定位設備中心到多波束換能器中心的偏心改正量為(Δxa,Δya,Δza)。利用坐標旋轉矩陣,可得在站心大地坐標系中,換能器中心與定位設備中心不一致引起的動態偏心改正模型:
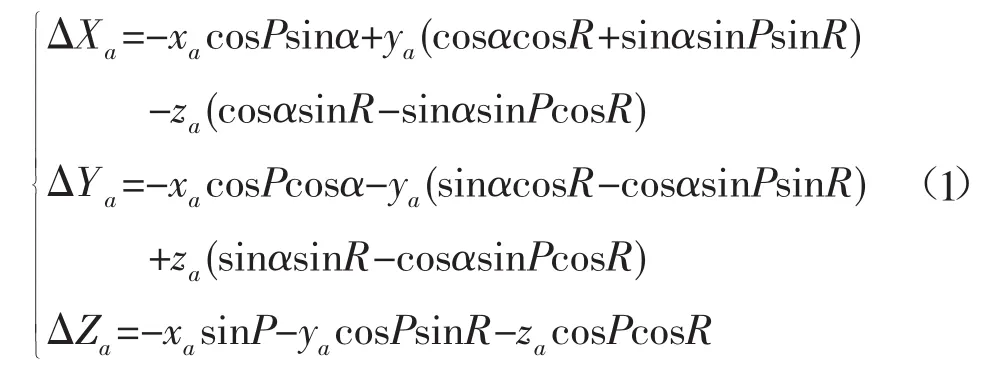
測點相對于換能器中心(坐標原點)在站心大地坐標系中動態位置傳算模型為:
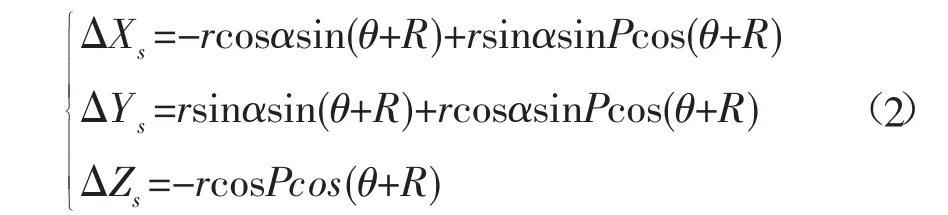
由于多波束測深系統定位和測深時間不同步帶來時延誤差,需要進行動態時延改正,改正模型為:
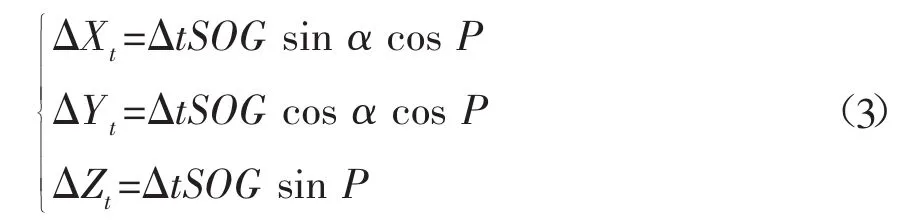
經過上述三項改正后,可將測點坐標從站心大地坐標系轉到定位系統所在坐標系,轉換公式為[10]:
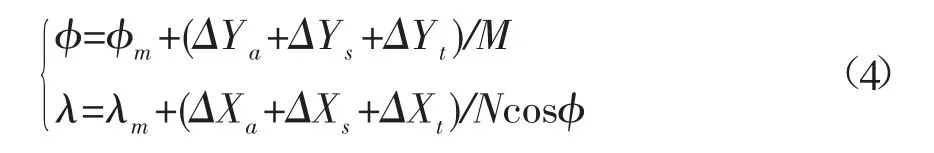
式中:φ為測點的緯度;φm為定位系統的緯度;λ為測點的經度;λm為定位系統的經度;M為子午圈曲率半徑;N為卯酉圈曲率半徑。此處認為M,N無誤差。
根據上述公式推導可以看出,影響測點位置歸算的誤差源主要包括:定位系統本身、定位設備中心相對于換能器中心的坐標xa,ya,za,橫搖角R、縱搖角P、航向角α、聲線傳播距離r、波束指向角θ、時延t和船速SOG構成。
2 測點位置歸算精度估計模型
2.1Rob Hare測點位置歸算精度估計模型
結合前面的位置誤差源分析,采用Rob Hare位置歸算精度估計模型進行計算,具體推導過程如下:
根據(4)式,可得測點位置歸算精度估計公式
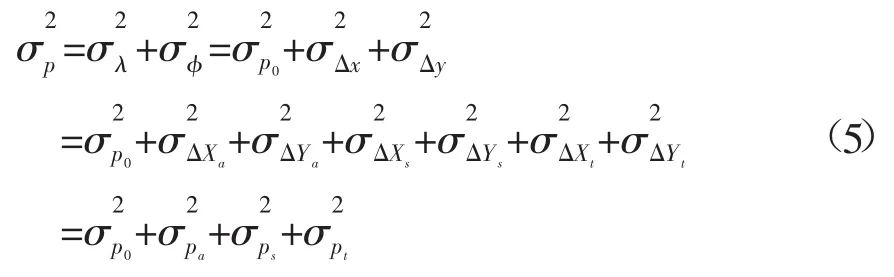
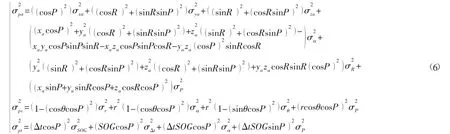
根據式(5)~式(6),可將總的測點位置歸算精度估計模型寫成如下形式:
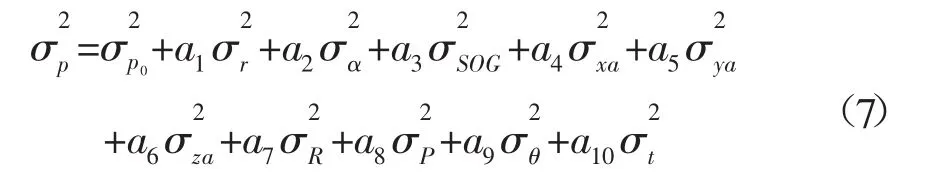
式中:系數a1,a2,…,a10分別表示各誤差源對測點位置歸算精度的影響量。
顯然,上述模型在推導過程中并未考慮到改正數之間的相關性,而從式(1)~式(3)可知,各項改正數均與橫搖、縱搖和航向角有關,因此它們相互之間是相關聯的,所以該模型存在一定的不足,最終得到的位置歸算精度也會受到影響。下面將對上述模型進行改進,推導過程中將顧及各改正數之間的相關性。
2.2改進模型
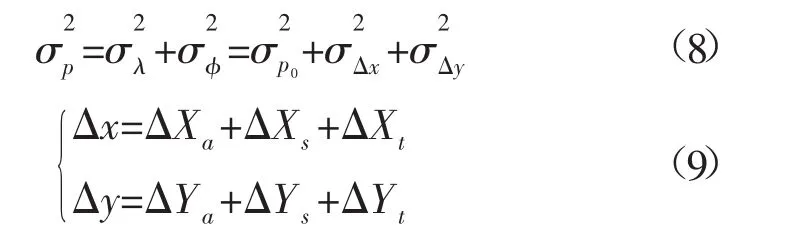
將式(1)~式(3)代入(9)式可得:
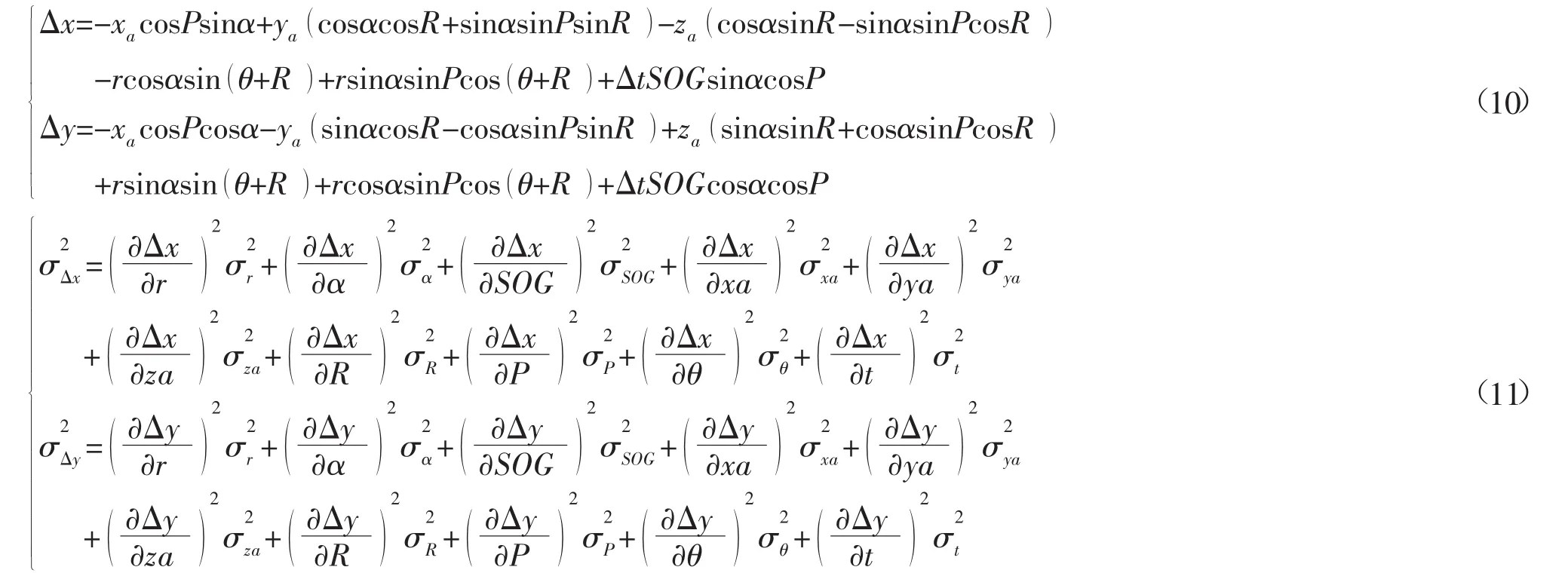
綜合式(8)~式(11),將總的測點位置歸算精度估計模型改寫成下式:
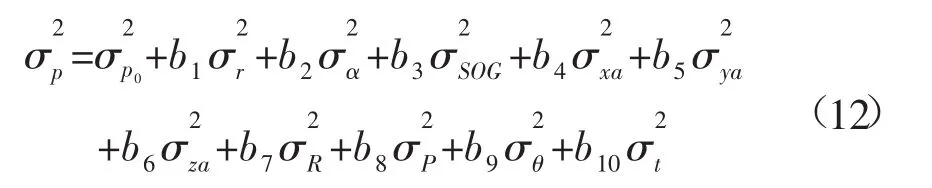
上述即為改進的測點位置歸算精度估計模型,其中系數b1,b2,…,b10分別表示各誤差源對測點位置歸算精度的影響量。
3 算例分析
假設實驗采用seabat8101多波束測深系統,工作頻率為240 kHz,姿態傳感器采用OCTANS III型運動傳感器,聲速測量使用SVplus聲速剖面儀,縱橫向波束角為1.5°,測量過程中多波束測深儀、傳感器部分參數及技術指標統計如表1~表2所示。
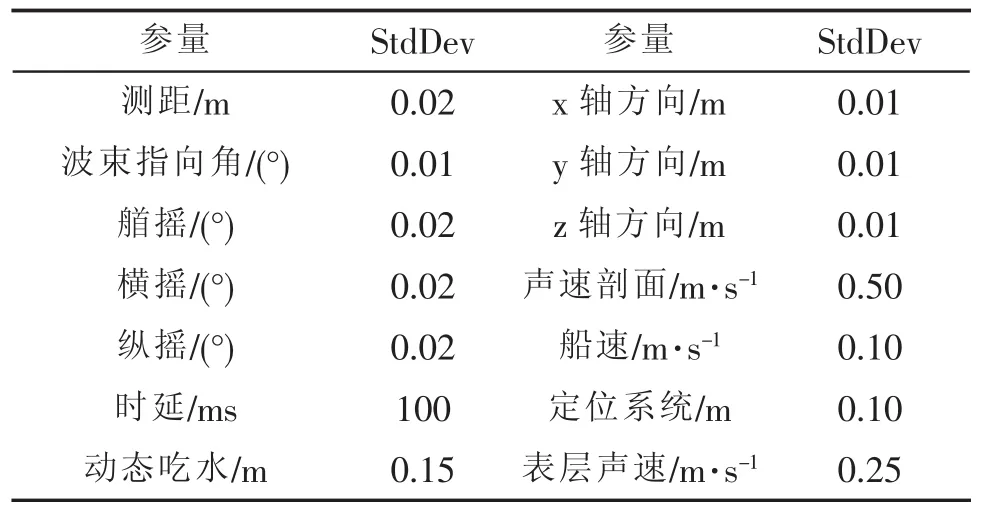
表1 多波束測深系統及傳感器的部分參數及技術指標
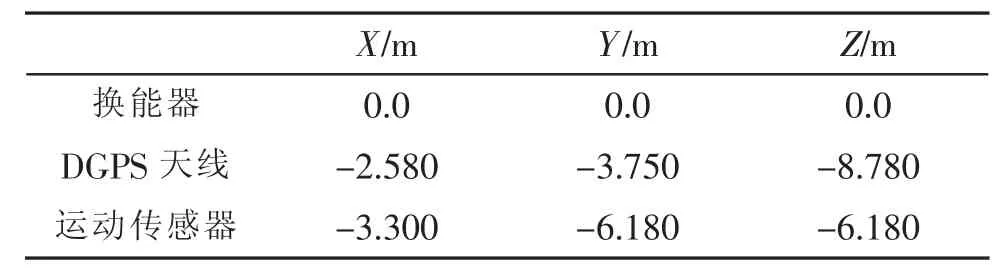
表2 各測量單元在載體坐標系中的空間位置
以一ping數據為例進行分析,該ping包含101個波束,水深為100 m,假設測船實時橫搖、縱搖、艏搖均為零,分別采用上述兩種模型對該ping中各個波束進行位置誤差估算。為敘述方便,下文分析中將兩種模型分別概括為模型一、模型二,將計算結果列于表3~表4中,為更加直觀顯示各誤差源對測點位置影響的變化規律,分別采用兩種模型繪制誤差曲線圖,如圖1~圖2所示,通過分析得到如下結論:
采用兩種模型推導的各誤差源對測點位置精度估計影響變化規律大體一致,其中航向角誤差、測距誤差以及波束指向角誤差呈U型分布,對位置歸算影響最為明顯,在中央波束附近對位置歸算影響最小,往兩側依次增大;波束指向角誤差在中央波束附近變化比較平坦,兩側波束變化劇烈;船速、X軸、Y軸、Z軸、橫搖、縱搖以及時延對測點位置歸算的影響不隨波束指向角變化而變化;采用兩種模型進行位置誤差估算的主要差異來自航向、橫搖、縱搖以及波束指向角誤差,其它誤差源對測點位置造成的影響相同。
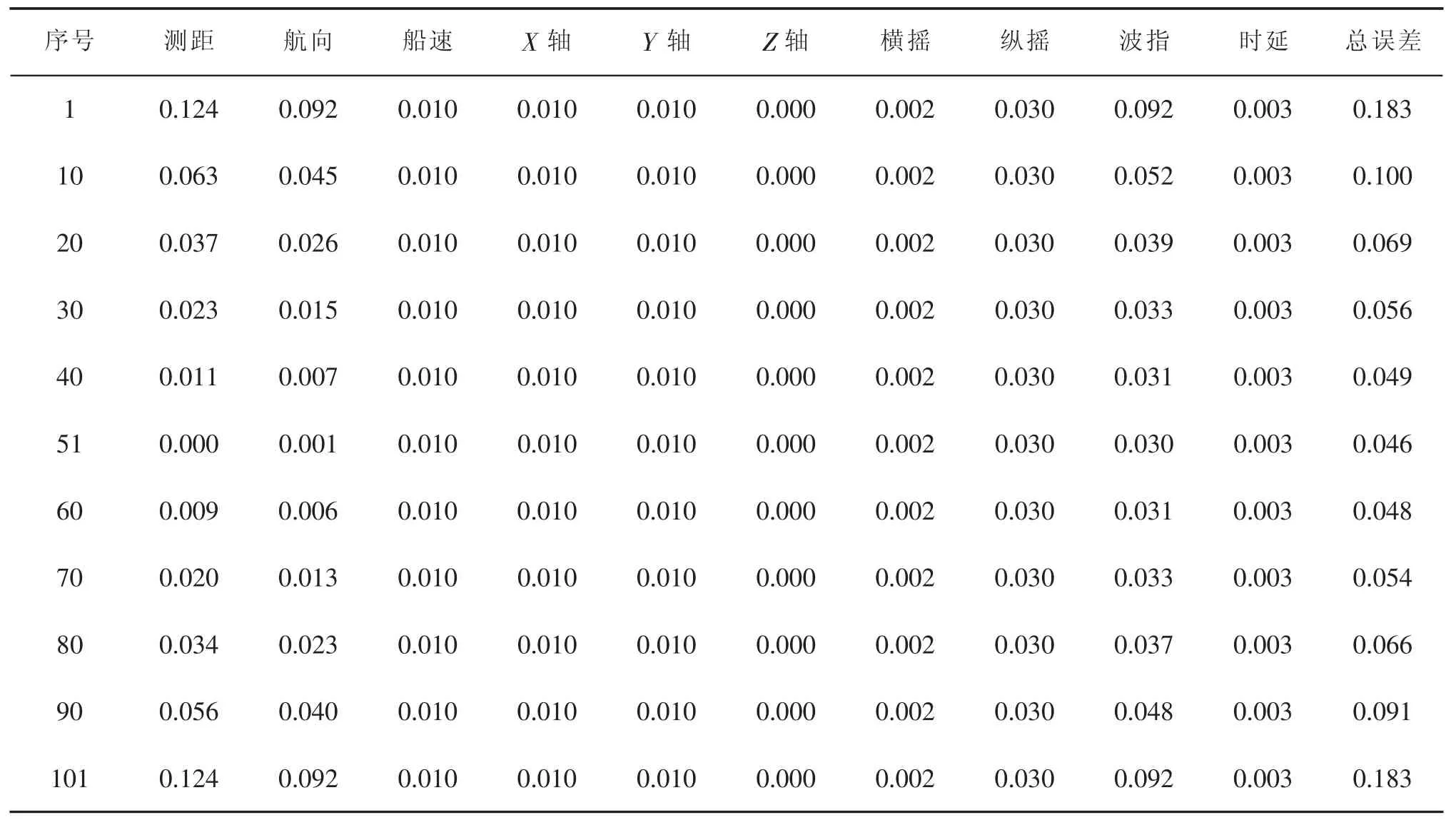
表3 采用模型一推導的各誤差源對測點位置影響值
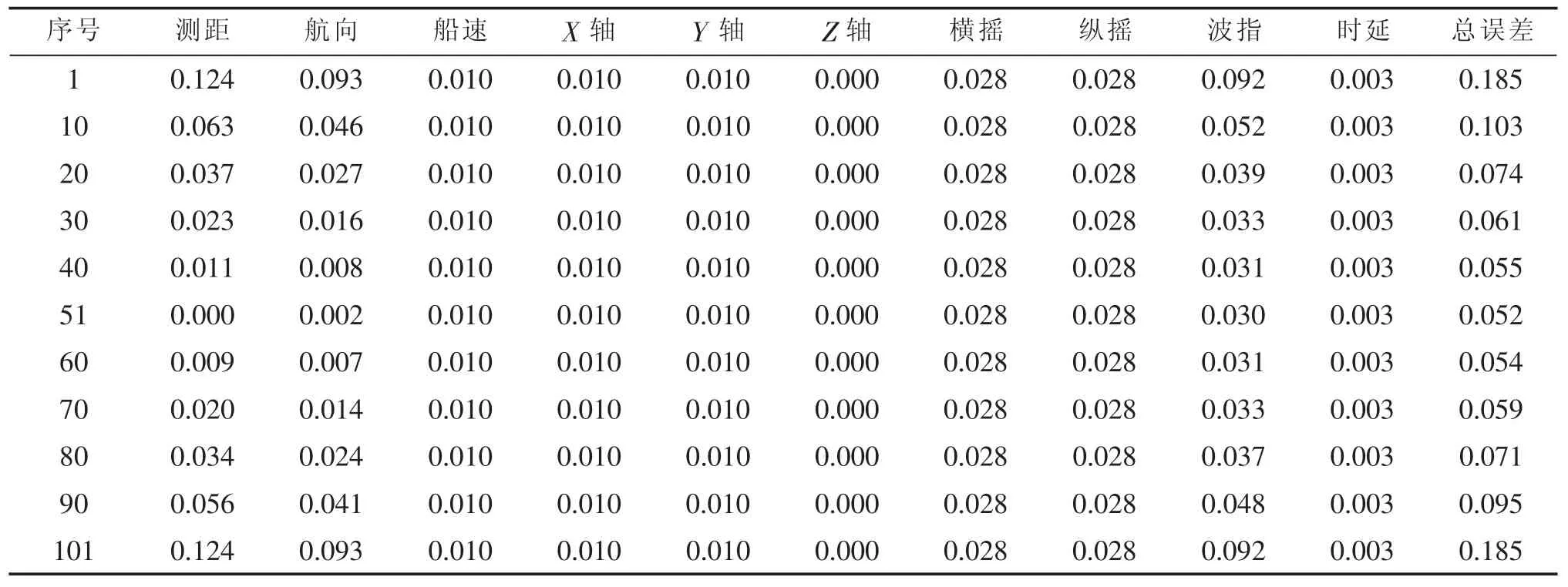
表4 采用模型二推導的各誤差源對測點位置影響值
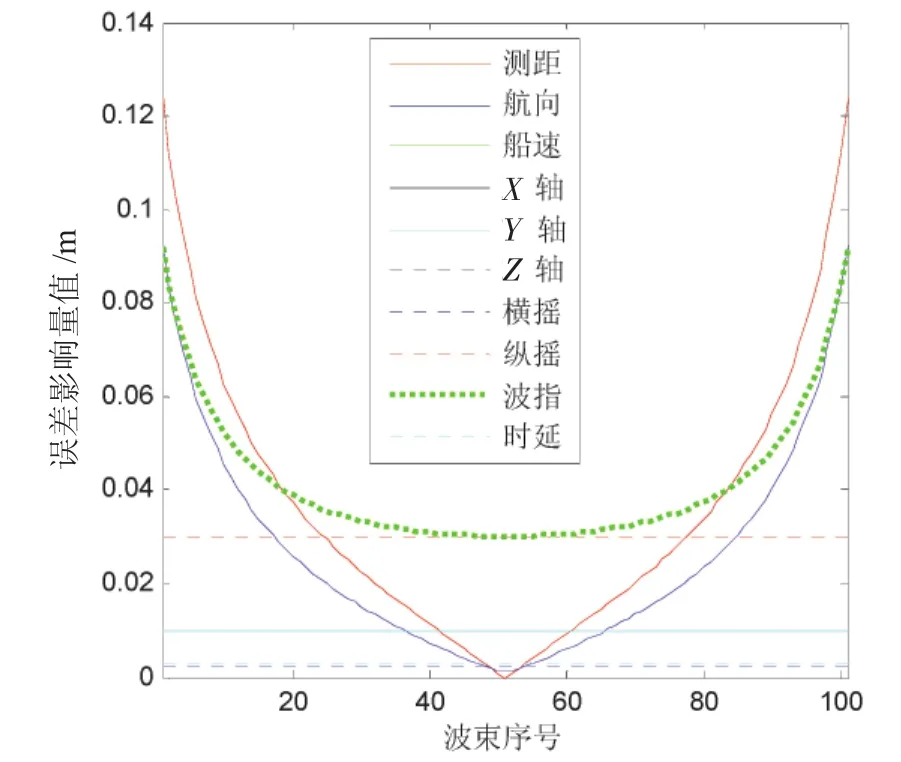
圖1 模型一繪制的誤差曲線圖
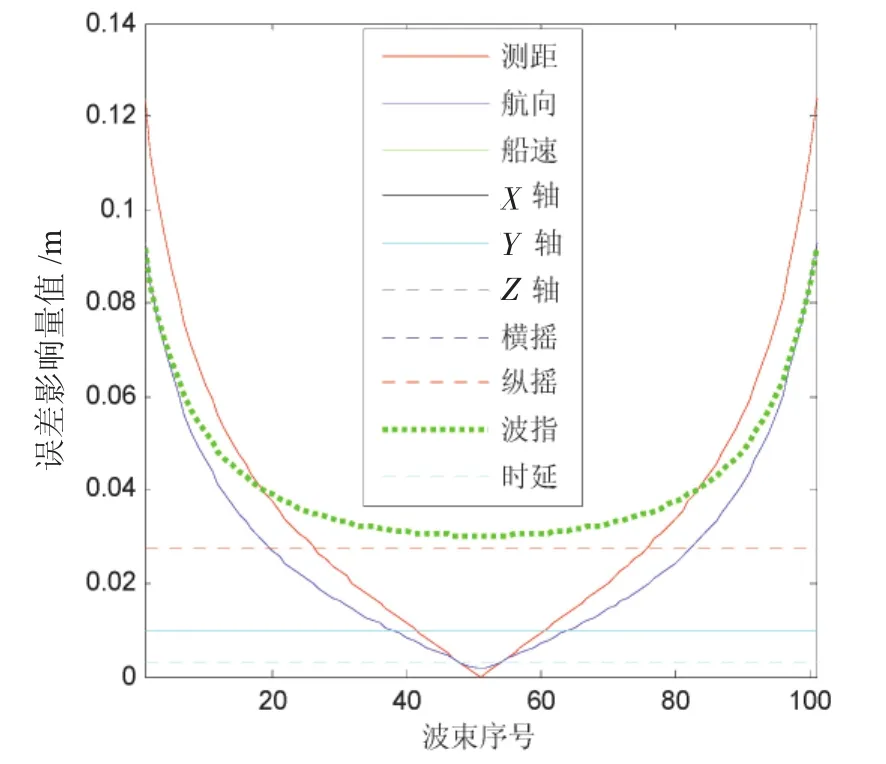
圖2 模型二繪制的誤差曲線圖
分別利用模型一與模型二繪制總位置誤差曲線,如圖3所示,采用模型二計算的總位置誤差值要略大于模型一計算出的值,這是由于模型一假設各改正數之間是相互獨立的,并未考慮各個改正數之間的相關性,可以將這部分差異暫且稱為改正數耦合誤差,其大小為圖3中采用模型一與模型二計算出的總誤差的差值。此外,在進行最終的測點位置歸算精度估計時,還需要顧及定位系統本身的精度σp0。
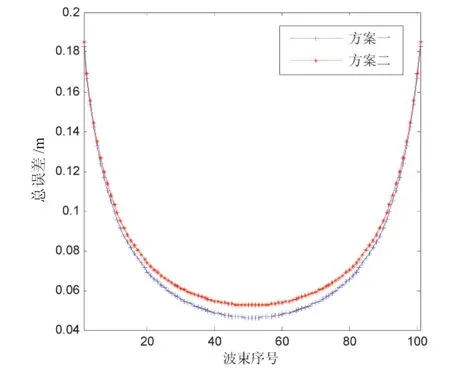
圖3 兩種模型計算的總位置誤差曲線圖
4 結論
多波束測點位置歸算是多波束測深數據處理的重要過程,位置歸算精度將直接影響最終測量成果的質量。本文針對Rob Hare推導誤差模型中的不足,建立了一種改進模型,并分別利用兩種模型計算出總位置誤差大小,分析了各誤差源對測點位置的影響規律,由于顧及到了位置歸算中各項改正數之間的相關性,新建立的誤差模型更加科學合理,最終測點位置歸算的精度能夠滿足測量成果需求,分析計算結果對多波束測深數據質量評估具有一定參考意義,同時可以根據給定的儀器參數深入挖掘測深設備潛能。
[1]陳非凡.多波束條帶測深儀研究發展動態[J].海洋技術,1999,18(2):26-32.
[2]李家彪,鄭玉龍,王小波,等.多波束測深及影響精度的主要因素[J].海洋測繪,2001(1):27-31.
[3]吳英姿,徐新盛,喬力爭.多波束測深系統的精度評估方法研究[J].海洋技術,2003,22(3):65-69.
[4]李宜龍,殷曉冬,張立華,等.交叉檢查法在多波束測深精度評估和誤差分析中的應用[J].海洋技術,2006,25(1):119-123.
[5]朱慶,李德仁.多波束測深數據的誤差分析與處理[J].武漢測繪科技大學學報,1998,23(1):1-4.
[6]陽凡林,李家彪,吳自銀.多波束測深瞬時姿態誤差的改正方法[J].測繪學報,2009,38(5):450-456.
[7]徐曉晗,劉雁春.海洋測深中時移和偏移效應綜合分析與改正[J].海洋測繪,2002,22(2):9-13.
[8]田勛,肖付民,朱小辰,等.多波束測深系統各誤差的傳播影響規律分析[J].海洋測繪,2011,31(1):24-28.
[9]Hare R.Depth and Position Error Budgets for Multibeam Echosounding[J].International Hydrographic Review,1995(2):37-69.
[10]黃謨濤,翟國君,謝錫君,等.多波束和機載激光測深位置歸算及載體姿態影響研究[J].測繪學報,2000,29(1):82-88.
[11]吳超,殷曉冬,張立華,等.基于不確定度的多波束測深數據質量評估方法[J].海洋測繪,2009,29(5):11-14.
[12]申家雙,黃謨濤,任來平.機載激光測深的位置歸算技術研究[J].海洋測繪,2003,23(5):55-60.
Study on the Effect of the Multibeam Echo Sounder Error Sources on Measurement Point Position Reduction
ZHANG Zhi-wei,BAO Jing-yang,XIAO Fu-min
Department of Hydrography and Cartography,Dalian Naval Academy,Dalian 116018,Liaoning Province,China
To resolve the problem of the insufficient precision estimation model for multibeam measurement point position reduction presented by Rob Hare,an improved model is built considering the correlation among corrections.On the basis of the new model,this paper analyzes the influence of various error sources on measurement point,and deduces the influence quantity of error sources on the reduction precision estimation of measurement point position.Combined with calculating examples,the error curve of each error source as well as the total position error curve are derived by using two kinds of models to calculate the influence level of error sources on measurement point position reduction.Through analysis and comparison of calculated results,the differences of the two models are obtained when assessing the reduction precision of multibeam measurement point position.In the light of the correlation among corrections,the improved model is regarded more scientific and reasonable.
multibeam echosounder system;position reduction;precision estimation;improved model;error curve
P237
A
1003-2029(2016)01-0074-05
10.3969/j.issn.1003-2029.2016.01.012
2015-03-09
國家自然科學基金資助項目(41074002,41576105)
張志偉(1987-),男,博士研究生,主要從事海道測量數據處理理論與方法研究。E-mail:zzwdljy@163.com

