淺海陣不變量和波導不變量關系的研究

董津生，張　爽，崔華義

（1.海軍海洋環境專項辦公室，天津　300042；2.國家海洋技術中心，天津　300112）

淺海陣不變量和波導不變量關系的研究

董津生1，張爽2，崔華義2

（1.海軍海洋環境專項辦公室，天津300042；2.國家海洋技術中心，天津300112）

陣不變量和波導不變量在淺海波導被動測距中應用廣泛，對于淺海垂直陣陣不變量和波導不變量的關系，可利用簡正波理論推導出陣不變量和波導不變量的關系式。利用2009年青島嶗山灣海試實驗垂直陣數據提取的陣不變量，以及通過實驗真實環境仿真得到的波導不變量，驗證了上述關系式。陣不變量和波導不變量關系的明確，理論上可以改善陣不變量測距精度，進一步擴大兩者的應用范圍。

陣不變量；波導不變量；簡正波俯仰角

在研究淺海波導聲場的干涉和多途結構時，研究人員提出了波導不變量和陣不變量的概念，并被廣泛用于解決淺海聲源被動測距等實際問題。波導不變量最早是由S.D.Chuprov［1］提出，在研究淺海波導中寬帶點源聲場的聲強、聲功率和聲壓譜密度等物理量在以水平距離和聲源頻率為坐標的二維平面（r-ω平面）上出現的條紋型分布時，為了解釋干涉條紋的產生機理而定義的，是一個以頻率、距離和干涉條紋的斜率為函數的標量參數。Brekhovskikh和Lysanov［2］考慮“一族”性質相近的簡正波構成的干涉聲場，對于參數隨距離不變的海洋波導給出了波導不變量的另一種表達形式，指出波導不變量近似是一個常數。陣不變量最早是由Sunwoong Lee和 Nicholas C.Makris［3-5］在研究利用聲陣列方法估計水平分層的海洋波導中的脈沖聲源距離時提出的，該方法對聲陣列利用傳統平面波束形成得到被動波束延遲時間角度的強度譜，從譜峰與延遲時間的關系得到陣不變量。尚啟春［6］通過簡正波理論在原始陣不變量定義的基礎上簡化了推導過程，利用簡正波的俯仰角和平均聲速，重新定義了物理意義更明確的陣不變量。張爽等［7］指出陣不變量測距的理論誤差與波導不變量有關。陣不變量和波導不變量有著特定的關系，它們不是絕對的不變量，與簡正波模態號數和頻率有關。本文基于簡正波理論對兩者的關系進行了深入研究，并通過海試實驗和數值仿真進行了驗證，明確了陣不變量和波導不變量的關系，給出了進一步提高陣不變量測距精度依據，擴大了陣不變量和波導不變量的應用范圍。

1　淺海波導不變量和陣不變量的關系理論推導

1.1淺海簡正波聲場

簡正波描述的寬帶點聲源的頻域聲壓為：

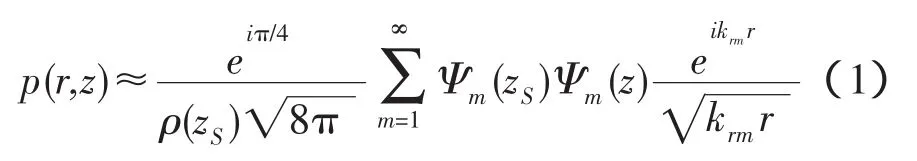
式中：m代表簡正波號數；Ψm（z）為簡正波模態函數；krm為水平波數；ρ為密度；z代表深度；zS為聲源深度；r代表水平傳播距離。

簡正波的水體平均速度由相速度和群速度定義：

式中：相速度vpm=ω/krm；群速度vgm=dω/dkrm；ω為角頻率。

簡正波的俯仰角φ表示傳播方向和垂直方向的夾角，其正弦值可表示如下：

式中：k=ω/c為波數；c為水中聲速。

1.2陣不變量

陣不變量原始定義如下：

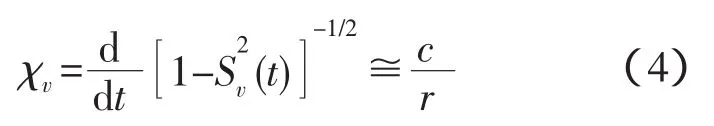
式中：Sv為波束形成的時延。

基于簡正波理論的陣不變量存在更簡單的形式，推導如下：

簡正波的到達時間由群速度決定：

式（3）、式（5）相乘可以得到：

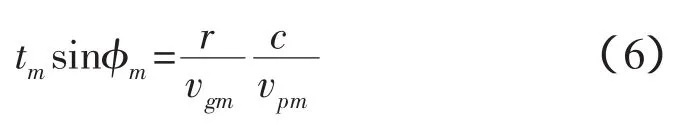
式（7）右端與簡正波號數和頻率無關，則定義陣不變量為：

此種陣不變量為時間和俯仰角余割值曲線的斜率，可通過陣波束形成在時間和俯仰角輸出強度譜上峰值搜索擬合直線得到，因此是各號簡正波的平均結果。

由式（7）～式（8）可以看出，

本質上陣不變量是聲信號在聲速c0水體里傳播到r距離的絕對時間的近似值［6］。

1.3波導不變量

波導不變量的原始定義如下：

對于水平環境近似不變的海洋波導中，簡正波聲場中任意兩號簡正波波導不變量在數值上等于簡正波相慢度差與群慢度差比值，考慮一組簡正波的干涉波導不變量β可表示為：

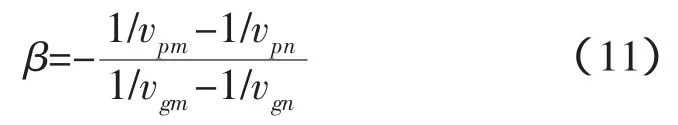
不同號簡正波群速度和相速度存在差異，同號簡正波的兩種速度只有在遠離截止頻率的時候隨頻率才是弱依賴，所以波導不變量也不是絕對不變的。波導不變量也是針對某“一族”性質相近的簡正波近似為一個常數［2］。

1.4陣不變量與波導不變量的關系

在水平環境近似不變的淺海波導中，任意兩號簡正波經遠距離傳播，到達時間存在差異：

俯仰角也存在差異：

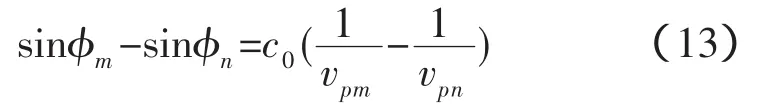
式（12）/式（13）可得：

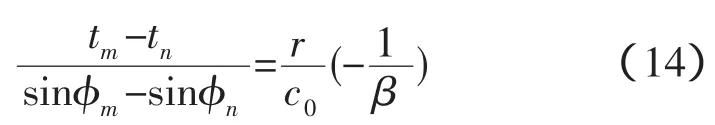
代入式（8）陣不變量的定義，可得：

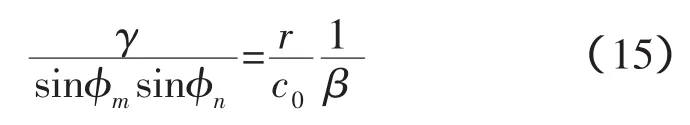
即聲信號傳播的真實絕對時間應該由陣不變量和波導不變量來共同描述：

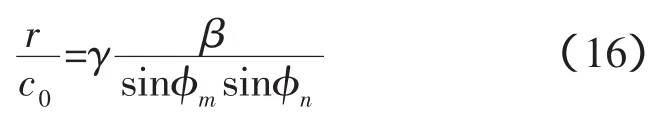
因此在水平環境近似不變的淺海波導中，真正的不變量是聲信號在聲速c0水體里傳播到r距離遠處垂直陣的絕對傳播時間，定義為“陣位置不變量”用η表示。

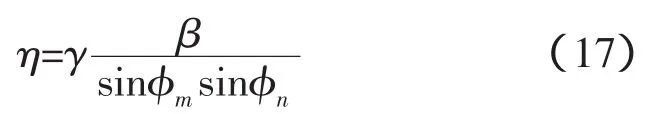
陣位置不變量由通常的陣不變量和波導不變量乘積以及簡正波的俯仰角共同決定。可見若運用陣不變量測距，會存在源自于波導不變量以及相應俯仰角正弦值的誤差。

2　陣不變量和波導不變量的海試與仿真處理

2.1垂直陣海試實驗及陣不變量提取

利用中國海洋大學水聲實驗室2009年青島嶗山灣海試垂直陣測量數據，進行陣不變量提取。實驗海域水深17 m，平均聲速為1 537 m/s，接收垂直陣陣元數15個，陣元間距1 m。共計處理5個站位的數據，5個站位垂直陣到聲源的水平距離分別為0.9 km，2.9 km，4.6 km，6.5 km，9.3 km。依據公式（8）提取陣不變量的信號處理流程如圖1。

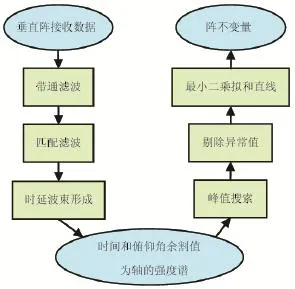
圖1　垂直陣接收數據處理流程圖

以站位3某一接收信號為例，給出信號處理過程。垂直陣原始接收信號進行帶通濾波和匹配濾波后的時域信號如圖2，可以明顯地看出1號、2號、3號簡正波依次到達。

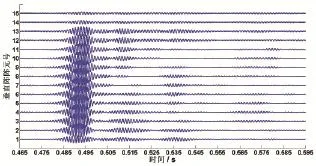
圖2　站位3某一接收信號帶通、匹配濾波后時域結果

對帶通匹配濾波后的陣列信號進行短時波束形成，俯仰角角度搜索范圍70～110°，角度分辨率為0.1°，移動時間窗長度取0.002 s，每個時間窗內信號分別做常規波數形成得到強度譜隨時間和角度的變化，如圖3，以最大值為參考，最大強度為0 dB。

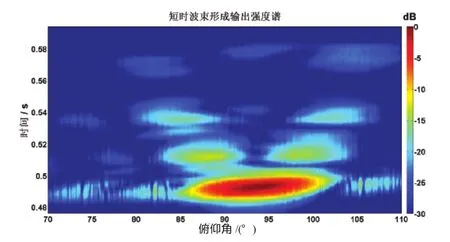
圖3　短時波束形成輸出的強度譜隨時間和俯仰角的變化

將俯仰角角度轉化為其相應的余割值，在以時間-俯仰角余割值為軸的強度譜（如圖4）間軸搜索譜峰，剔除異常值（紅色*表示）后，利用譜峰點（黑色*表示）通過最小二乘擬合直線，根據公式（8）直線的斜率即為陣不變量，此處γ=2.504 8。

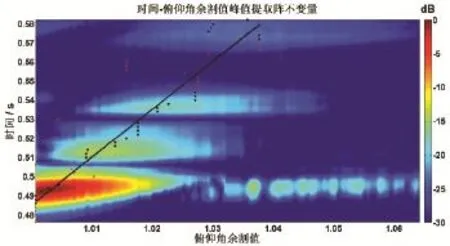
圖4　強度譜隨時間和俯仰角余割值變化提取陣不變量

對5個站位，每個站位選取18個接收信號分別提取陣不變量，多次結果如圖5。對多次結果統計平均，得到各站位的波導不變量值的平均結果，如表1，可見站位1到站位5的陣不變量值依次增大，這是由于站位1到站位5的水平距離依次增大，但是陣不變量的值均小于陣位置不變量（聲源到垂直陣的絕對傳播時間），符合前面的理論推導，這種差異根據公式（17）可知是β/（sinφmsinφn），這正是波導不變量和陣不變量的關系所在。就此可以估計出β/（sinφmsinφn），的值，各站位結果平均值為1.289，隨陣不變量值（即聲源到垂直陣距離）的增大而減小，但這是全部簡正波的平均結果，具體主要是由哪號簡正波的波導不變量決定的，需要通過下文仿真分析給出。

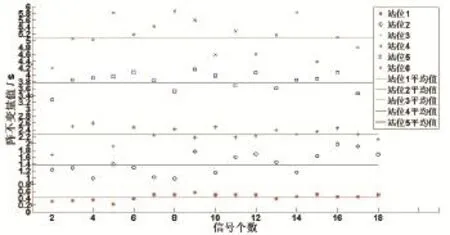
圖5　5個站位提取陣不變量統計結果

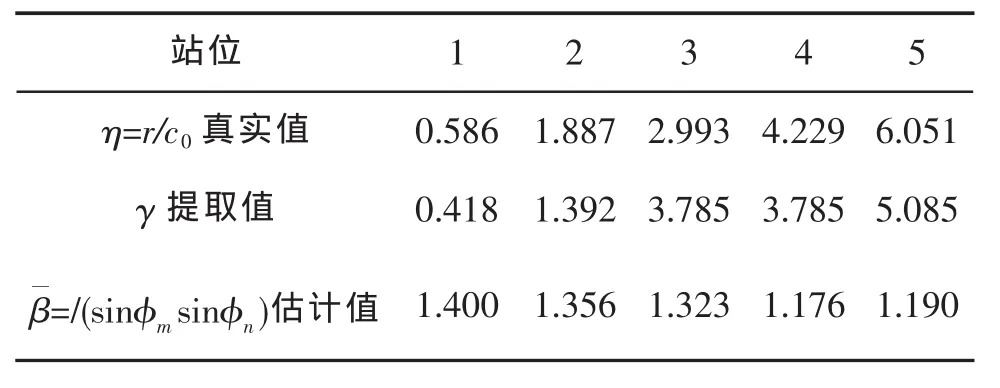
表1　各站位提取波導不變量的平均結果

2.2仿真提取波導不變量

根據海試真實實驗環境，利用KRAKEN模型仿真得到簡正波聲場，進而提取波導不變量。仿真所設的波導環境參數如圖6所示，聲速剖面取5站位傳播實驗時間內的平均聲速剖面，海底聲速1 697 m/s，密度取1.866 g/cm3，吸收系數取0.677 dB/波長，根據信號頻帶設置頻率為720～920 Hz，間隔為1 Hz。

圖6　仿真波導環境

由于實驗信號明顯可分離前四號簡正波，因此分析前四號簡正波的特征。前四號簡正波相速度、群速度、及各自的平均速度隨頻率的變化如圖7所示，對個各號簡正波來說，相速度＞平均速度＞群速度，相速度隨頻率增大而減小，群速度隨頻率增大而增大，平均速度均與水體的深度平均速度可近似相等，證明了公式（7）的假設成立。圖8給出了前四號簡正波俯仰角余割值隨頻率的變化，各號簡正波俯仰角余割值均隨頻率增大而減小，各號簡正波俯仰角余割值與圖4所示實驗結果基本一致。

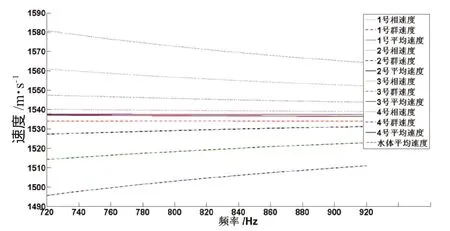
圖7　前4號簡正波相速度、群速度、平均速度隨頻率變化

圖8　前四號簡正波俯仰角余割值隨頻率變化

根據公式（12）可以求出不同號簡正波間的波導不變量值，如圖9所示，只有12號簡正波的波導不變量值β12隨頻率增大，取值范圍1.094～1.826，平均值為1.346。其他波導不變量值均隨頻率增大而減小，但接近于1，具體均值見表2。

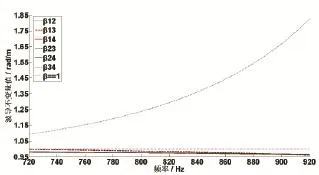
圖9　不同號簡正波間波導不變量隨頻率變化

為了與實驗結果比較分析，圖10給出了βmn/（sinφmsinφn）隨頻率變化的結果，只有12號簡正波結果隨頻率增大而增大，取值范圍為1.103～1.835，平均值為1.355。其它各號組合的波導不變量與其相關俯仰角正弦值比值結果均隨頻率增大而減小，均值均在1附近，具體見表2，所有結果的平均值為1.06。

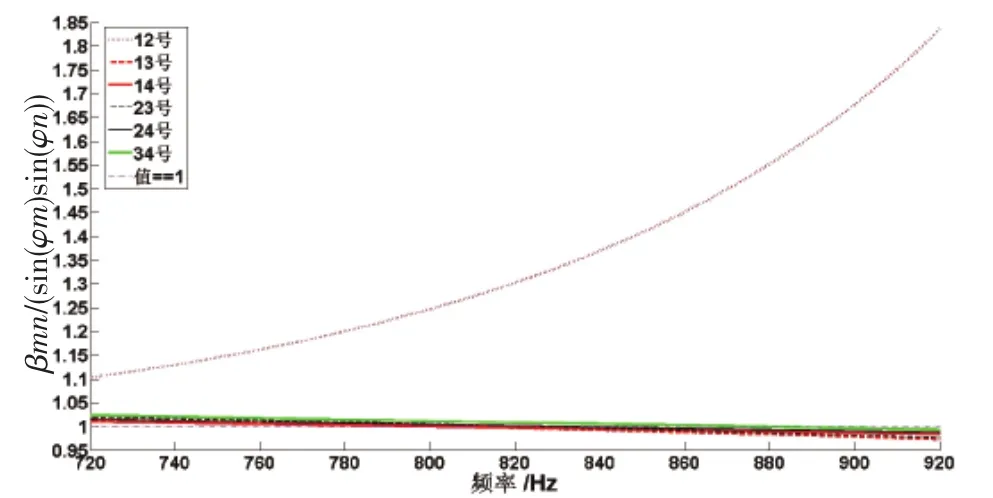
圖10　波導不變量與相關號俯仰角正弦值比值隨頻率變化

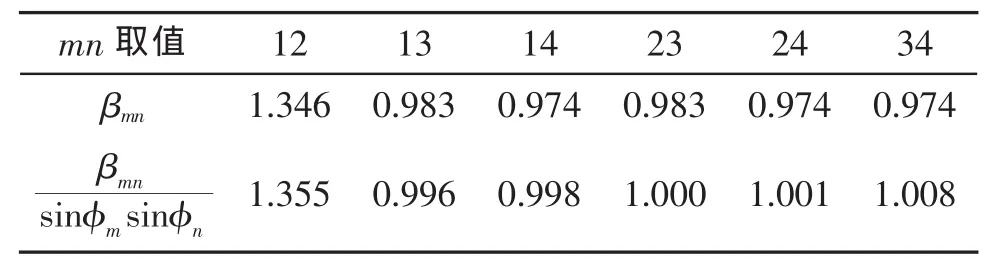
表2　仿真提取波導不變量的平均結果

1號站位、2號站位的βmn/（sinφmsinφn）值與其他兩個站位的值差異巨大，完全取決于波導不變量的值，1號和2號站位波導不變量的值之所以沒有在1附近，是因為聲速剖面的負梯度導致的1號簡正波主要在水體下部傳播，從圖11中心頻率820 Hz的前4號簡正波模態函數的深度分布情況可以清楚地看出1號簡正波的模態函數分布在下部水體，中心位置在13 m，而其他各號簡正波全水體分布，中心位置在10 m，1號簡正波和2號簡正波的分布差異導致了波導不變量值遠大于1，從而導致β12/（sinφ1sinφ2）的值也遠大于1，其他號簡正波分布特征相似，可以稱作一族簡正波，相應的波導不變量值接近1（小于1），βmn/（sinφmsinφn）值也接近1。

圖11　前4號簡正波模態函數（820 Hz）

2.3實驗和仿真結果綜合分析

本節對垂直陣海試提取的陣不變量值和根據實驗真實環境仿真提取的波導不變量值進行比較分析。由表1可知，實驗中通過陣不變量估計的βˉ/（sinφmsinφn）值是各組波導不變量的平均結果，這是由于陣不變量是各號簡正波的平均結果的緣故。實驗得到的各站位的平均結果為1.289，與仿真中β12/（sinφ1sinφ2）的值1.355更接近，說明了1號、2號簡正波的波導不變量起主要作用，圖2～圖3顯示實驗海域波導中遠距離垂直陣接收的信號能量也說明了簡正波能量分布從低號到高號依次遞減。實驗中值隨距離增大反而減小也可以通過圖10解釋，對于寬帶信號，高頻衰減得快，遠距離聲場低頻部分能量大，而低頻部分的β12/（sinφ1sinφ2）比高頻部分的值小。

實驗和仿真驗證了波導不變量和陣不變量滿足關系公式（17），波導不變量與陣不變量均不是絕對不變量，其乘積除以相應俯仰角的正弦值才是不變的，這里稱之為陣位置不變量。對于本次實驗，由于負聲速梯度，導致了1號簡正波主要在水體下部分傳播，與其他號簡正波分布存在明顯差異，因此1號、2號簡正波波導不變量遠大于1（1.1～1.8），而其他模態間的波導不變量值均接近1（小于1），從而導致了β12/（sinφ1sinφ2）的值遠大于1（1.1～1.8），其他模態間的βmn/（sinφmsinφn）的值均接近于1，這與實驗求得陣不變量與陣位置不變量的偏差相一致。由此應用陣不變量測距時，應該尋找陣不變量和位置不變量偏差小的部分提取陣不變量，從而提高測距精度。

3　結論

本文基于簡正波理論研究了淺海聲波導中陣不變量和波導不變量的關系：波導不變量和陣不變量的乘積除以相應簡正波俯仰角的正弦值等于聲源到垂直陣的絕對傳播時間。利用2009年嶗山灣海試實驗中5個站位的數據提取了陣不變量，其值均小于聲源到垂直陣的絕對傳播時間（陣位置不變量）。實驗提取的陣不變量是各號簡正波的平均結果，通過本文推導的波導不變量和陣不變量的關系進一步得到波導不變量和俯仰角正弦比值的實驗平均結果為1.289。應用海試真實環境參數仿真可知，在負梯度聲速剖面下1號簡正波主要在水體下部傳播，而高號簡正波的能量在全水體均有分布。1號、2號簡正波波導不變量和相應俯仰角正弦比值在1.1～1.8之間，與其他各號波導不變量和相應俯仰角正弦比值的值近似等于1明顯不同。波導不變量和俯仰角正弦比值的實驗平均結果在1號、2號簡正波波導不變量和相應俯仰角正弦比值范圍內，驗證了本文提出的波導不變量和陣不變量關系。對于負梯度聲速剖面海洋波導，各號簡正波存在不同分布特征（低號在水體下部傳播）時，陣不變量值與聲信號從聲源到垂直陣的傳播時間差異較大，利用陣不變量測距方法可能失效，應濾除分布特征差異大的低號簡正波再進行陣不變量提取，從而準確估計距離。陣不變量和波導不變量關系的明確，對于基于陣不變量和波導不變量進行測距等應用具有一定的指導意義，下一步會繼續研究。

致謝：感謝中國海洋大學水聲實驗室提供的2009青島嶗山灣海試垂直陣數據。

［1］SDChuprov.Interference Structure ofa Sound Field in a Layered Ocean［C］//LMBrekhovskikh et al.eds:Ocean Acoustics，Moscow: Nauka，1982.71-91.

［2］LMBrekhovskikh，Yu LysanovFundamentals ofOcean Acoustics［M］.3rd ed.NewYork:Springer-Verlag，2003.

［3］Sunwoong Lee，Nicholas Cmakris.A New Invariant Method for Instantaneous Source Range Estimation in an Ocean Waveguide from Passive Beam-Time IntensityData［J］.J Acoust Soc Am（S0001-4966），2004，116（4）:2646.

［4］Sunwoong Lee，Nicholas Cmakris.Range Estimation ofBroadband Noise Sources in an Ocean Waveguide Using the Array Invariant［J］.J Acoust Soc Am（S0001-4966），2005，117（4）:2577.

［5］SunwoongLee.Nicholas Cmakris The ArrayInvariant［J］.J Acoust Soc Am（S0001-4966），2006，119（1）:336-351.

［6］尚啟春.淺海波導中寬帶聲源被動測距研究［D］.青島：中國海洋大學，2011.

［7］張爽，尚啟春，張寅權，等.寬帶聲源測距的陣不變量方法研究［J］.聲學技術，2012，31（4）：420-423.

Study on the Relationship Between Waveguide Invariant and Array Invariant in Shallow Sea

DONG Jin-sheng1，ZHANG Shuang2，CUI Hua-yi2
1.Marine Environment Special Office of the PLA Navy，Tianjin 300042，China；
2.National Ocean Technology Center，Tianjin 300112，China

Both array invariant and waveguide invariant are widely used in passive ranging in shallow water acoustic study.In this paper，their relationship has been derived with the normal mode theory and has been verified by experiment data.The array invariant is extracted from the signals received by a vertical array in the Laoshan Bay sea test in 2009 in Qingdao，Shandong Province，and the waveguide invariant is obtained by simulation of real environment.Experiment results are in accordance with the theoretical equation.The combination of waveguide invariant and array invariant can improve the accuracy of passive ranging and enlarge the application scope of both techniques.

array invariant，waveguide invariant，normal mode elevation angle

O427

A

1003-2029（2016）02-0060-06

10.3969/j.issn.1003-2029.2016.02.011

2015-12-18

董津生（1968-），男，高級工程師，主要研究方向為海洋環境調查、數據分析應用。E-mail:123456789msn@sina.com