基于三種亞格子模型的空腔振蕩流動計算

白海濤， 賴煥新（華東理工大學承壓系統與安全教育部重點實驗室，上海 200237）

基于三種亞格子模型的空腔振蕩流動計算

白海濤， 賴煥新
（華東理工大學承壓系統與安全教育部重點實驗室，上海 200237）

使用三種亞格子應力模型，對長深比（L/D）為5的三維矩形開式空腔的可壓縮流體進行大渦模擬計算。研究得到的空腔自激振蕩頻率與Rossiter公式計算結果和實驗結果吻合良好，結果顯示振蕩能量主要集中在較低頻率區域，壓力幅值主要出現在前三階模態。Dynamic Smagorinsky-Lilly（DSM）模型在空腔前后壁面附近區域的脈動強度分布比Smagorinsky-Lily （SM）模型更為接近實驗值，Wall Adapting Local Eddy Viscosity（WALE）模型的脈動強度分布與實驗值最為接近。由空腔底部監測點聲壓級分布及聲壓頻譜圖可以看出：WALE模型性能最佳，DSM模型結果也與實驗結果相符合，SM模型的預測性能略差。

開式空腔；自激振蕩；大渦模擬；亞格子應力模型；氣動噪聲

流體流過物體表面的空腔或缺口時，由于腔外剪切流與腔內流動的相互作用，會出現自激振蕩現象，同時出現劇烈的壓力、速度脈動，并輻射產生強烈的噪聲，該物理現象稱為空腔自激振蕩。空腔自激振蕩現象廣泛存在于飛行器的起落架艙、武器艙及燃燒室等部位，是典型的聲-渦干涉、非定常流和流體動力不穩定問題。從20世紀50年代開始，人們對空腔自激振蕩流動特性做了大量研究。關于開式空腔自激振蕩物理機制，雖然有多種解釋，但最被人們接受的是Rossiter［1］提出的空腔流聲共振反饋模型并給出了預估振蕩頻率的半經驗公式，該公式在一定精度范圍內能夠較為準確地預測空腔流激振蕩的峰值頻率，成為評價數值模擬結果的重要標準。

隨著計算流體力學的發展，空腔聲學特性的數值研究得到廣泛開展［2］。湍流直接模擬（DNS）能夠分辨所有能量尺度的渦，但目前局限于低雷諾數的情況。雷諾平均（RANS）能夠較為準確地預測前幾階模態頻率，但由于平均方法抹掉了湍流脈動部分信息，對于脈動強度的預測存在偏差。大渦模擬（LES）使用網格尺度的空間平均和濾波，可以保留大尺度渦運動湍流瞬態信息［3］，是目前被認為最有前景的數值方法。目前被廣泛應用的亞格子湍流模型有Smagorinsky-Lily（SM）模型、Dynamic Smagorinsky-Lilly（DSM）模型和Wall Adapting Local Eddy Viscosity（WALE）模型。SM模型［4］適用于各向同性的湍流流動計算，因為形式簡單，應用方便而得到廣泛使用。湍流在黏性底層的脈動很小，相應的雷諾應力也很小，而壁面附近速度梯度卻很大。此時，在壁面附近SM模型產生過大的耗散，尤其在邊界層轉捩問題中，往往抑制了轉捩的發生或導致流動重新層流化［5］。為了彌補SM模型的缺陷，Germano等［6］提出DSM模型，通過建立隨著時間與空間變化的亞尺度黏性系數公式，給出固體壁面上正確漸進關系，并能預測能量逆向傳遞因而得到更廣泛關注。Moin等［7］于1991年將DSM模型應用于可壓縮湍流。然而，DSM模型在某些流場中會得到不合理亞格子黏性系數［8］。Nicoud等［9］于1999年提出WALE模型，該模型采用速度梯度張量的平方，除了變形率張量，還考慮了旋轉張量的影響，在近壁面尺度下可以較好得到渦黏性。

雖然前人在空腔自激振蕩方面做了很多工作［10-11］，但迄今為止，關于不同亞格子模型在預測空腔自激振蕩方面的差異鮮見報道。本文采用SM、DSM和WALE三種亞格子模型對空腔自激振蕩流動特性和振蕩機理進行分析，并將模擬計算結果與實驗結果進行對比，分析這三種亞格子模型的優劣，為進一步研究空腔自激振蕩發聲機理提供參考和借鑒。

1　研究對象及網格

本文研究對象是M219三維矩形空腔［12］，長深比L/D=5。因為該空腔底部不會出現剪切層再附著情況，按照空腔靜態流動特性［13］，該空腔為開式空腔。自由來流馬赫數為M=0.85，進口滯止壓力p0=100 996 Pa，滯止溫度T0=309.3 K，對應的自由流速度U∞=280.2 m/s，基于空腔長度的雷諾數ReL=6.8×106。計算區域由空腔和空腔上方主流區域兩部分組成，坐標原點在空腔底板中心處，主流區長（L′）、寬（W′）、深（D′）分別平行于空腔長（L）、寬（W）、深（D）。對整個流體區域劃分結構網格，網格采用分區劃分和局部加密技術，離壁面近處稠密，遠離壁面稀疏［2］。模型尺寸及網格分布情況如表1和圖1所示，表1中Y＋表示第一層網格到壁面距離的量綱為一量，用來考察網格質量的優劣。

表1　模型尺寸及網格參數Table 1 Model size and mesh parameters

圖1　計算區域及網格分布情況Fig.1 Computational domain and distribution of the grid

在空腔底板Y=－25.4 mm的線上均勻分布P1～P10共10個監測點，點與點之間的距離為50.8 mm，10個監測點位置對應英國國防科技公司QinetiQ對該空腔進行壓力脈動測量實驗的監測點，各個監測點分布情況如圖2所示。

圖2　監測點分布Fig.2 Distribution of monitoring points

2　數值計算方法

2.1控制方程與方法

可壓縮流動的連續方程、動量方程和能量方程的量綱為一形式如下：

其中：i，j分別表示沿x，y方向分量；ρ，t，u，p分別表示密度，時間，速度，壓力；σ，ET，q，S分別表示正應力，總能量，熱通量和源項；符號頂部“－”表示普通濾波變量；“～”表示Favre濾波變量。

參考進口自由流變量進行量綱為一化，參照長度為空腔深度。亞格子應力張量τij有如下定義：

采用Boussinesq假定，亞格子應力使用式（5）計算：

其中：μt為亞網格湍流黏性力；τkk為亞網格尺度各向同性的部分；δij為應變率；S—ij為應力張量的速率，定義為

計算時依據實驗數據，進口給定總溫T0和總壓p0，出口給出無反射壓力邊界條件，主流區前、后、上表面采用對稱邊界條件，其他面為無滑移固體壁面。使用Fluent軟件計算流場，采用標準k-ε模型計算得到的穩態流場作為LES的初始場。LES模型中的亞格子湍流模型分別選取SM、DSM 和WALE模型，壓力-速度耦合采用PISO算法，動量方程使用二階迎風格式離散。時間推進步長為5×10－6s，相當于流體從流場流入到流出時間的1/1 488，計算總時長為0.3 s。

2.2三種亞格子（SGS）模型

SM模型是參照雷諾平均模式最早提出的SGS渦黏模型，以各向同性湍流為基礎，認為亞網格湍流具有混合長度型渦黏系數：

1

DSM模型通過兩個不同的亞尺度應變率張量，從已求解的區域信息計算得到Cs，Cs使用以下公式計算：

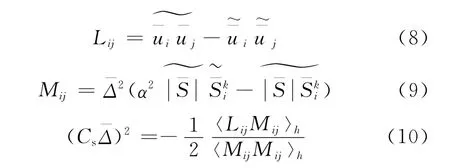
其中：Lij和Mij為二階張量；k和h為常數；a為濾波寬度比為格子過濾尺寸，模型中的其他參數與SM模型計算方法相同。模型系數Cs在空間上的變化會導致計算不穩定，為了保證計算穩定，通常將模型系數在空間沿均勻流動方向進行特定的平均處理。

在WALE模型中，渦黏模型：

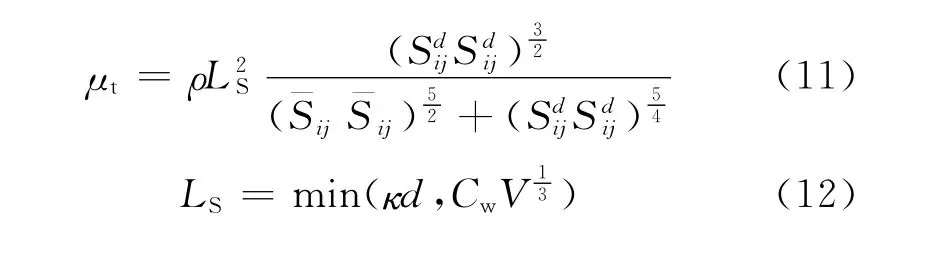
其中：Cw默認為0.325；gij為浮力產生項，其他符號與SM模型相同。WALE模型針對近壁面的流動，優化了亞網格黏性的計算方式，使預測結果更加符合真實的流動。

3　結果分析

3.1空腔的平均特性

圖3給出了三種亞格子模型XOZ中心對稱面平均流向速度和平均縱向速度分布情況。

圖3中1.0＜Z/D＜2.0的區域表示主流區，三種模型的平均流向速度和平均縱向速度在主流區均吻合良好，表明了數值模擬的準確性。由于剪切流與腔內流動的相互作用，空腔內特別是空腔后壁面附近會出現劇烈的壓力和速度脈動，渦黏模型的過分耗散會降低局部有效雷諾數［10］，導致各個亞格子模型在0＜Z/D＜1.0范圍內的平均流向速度和平均縱向速度均有所差異。從總體上看，SM模型平均流速分布與DSM模型和WALE模型差異較大，主要是由于在空腔壁面附近存在強剪切作用，小尺度渦的強度會得到明顯加強，導致渦的黏性耗散作用比SM模型給定的要強，從而出現了上述差異［14］。在流場復雜多變的空腔后壁面處，WALE模型的平均縱向速度表現出與SM和DSM模型的差異，是由于上游剪切層產生的渦核與空腔后壁面發生碰撞，變成碎片并表現出高度的不規則性，造成空腔后壁面處速度分布不具備嚴格的周期性［10］，因此，即使采樣時間足夠長，不同模型的采樣時間平均值也會有一定差異。另一方面，本文LES采樣時間可能還不夠長，也是造成上述差異的原因。

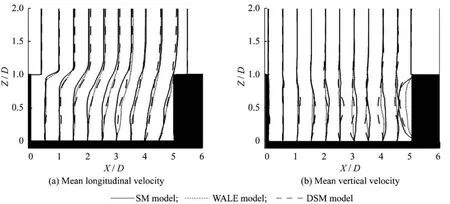
圖3　XOZ中心對稱面平均流向速度和平均縱向速度Fig.3 Mean longitudinal velocity and mean vertical velocity of the central XOZ plane

圖4所示曲線為圖2中10個監測點所在Y= －25.4 mm線上的聲壓級（SPL）分布情況，三種亞格子模型的預測結果都比實驗值略高，是由于當用LES計算具有強剪切運動湍流時，常用的亞格子模型都會出現平均值偏高的現象［14］。自激振蕩能量從空腔后壁面到前壁面大體上呈現單調遞減分布，主要是因為空腔內的自激振蕩由剪切層在空腔后壁面碰撞產生壓力波，當壓力波以渦旋的形式向上游運動時，一部分能量由于在空氣中傳播衰減而變弱，另外一部分能量在湍流運動中，由大尺度渦旋向小尺度渦旋逐級傳遞，直到有分子黏性起顯著作用的尺度，并在該尺度下耗散為熱能。因此，出現了下游自激振蕩能量比上游大的趨勢。

圖4　空腔底部Y=－25.4 mm處聲壓級分布Fig.4 Sound pressure level distribution of Y=－25.4 mm in the bottom of the cavity

由SM模型與實驗結果的對比情況來看，模擬值與實驗值差別最大的地方是在空腔前、后壁面附近區域，在這兩個區域，SM渦黏模型的過分耗散降低了局部雷諾數而使大尺度渦旋的預測結果比實驗值偏大［15］。DSM模型由于動態計算CS，使得空腔前、后壁面處的聲壓級得到明顯改善。WALE模型在空腔前半段與DSM模型預測結果一致，在后半段更加接近實驗值，明顯優于DSM模型，充分表現出其準確預測空腔底部聲壓級分布的優越性。

3.2空腔的瞬時特性

圖5給出了空腔自激振蕩已充分發展之后XOZ中心面一個周期（T）不同時刻的渦量等值線圖。在0.25T，空腔前緣剪切層形成了一個脫落渦（圖5 （a）），在0.50T～0.75T，脫落渦經過空腔中部繼續向下游發展，同時渦旋強度不斷加強（圖5（b）～圖5 （c）），一個周期結束時，第1個脫落渦與空腔后壁發生碰撞，碰撞后一部分渦沿著主流區向下游運動，另一部分沿著空腔后壁向空腔底部運動，此時空腔中下游區域產生劇烈的自激振蕩現象，同時，空腔前緣剪切層又形成一個新的脫落渦（圖5（d））。因此，空腔剪切層形成的具有一定脫落頻率的渦與空腔內流場發生相互作用，產生復雜的非定常特性。

圖5　空腔內瞬時渦量發展歷程Fig.5 Instantaneous vorticity development in the cavity

采用Q準則可以對流場的渦結構進行識別和顯示，定義為

其中，Dij和Ωij分別為速度梯度的對稱和反對稱量，因此Q是速度矢量梯度的第二Halmiton不變量，Q等值面包絡區定義了渦核分布情況。圖6給出了使用Q指標等值面定義的渦結構。可以看出在空腔前方及展向區域都沒有渦核的存在，由于Kelvin-Helmholtz作用，準周期性渦核在空腔前緣剪切層處產生并快速向空腔中下游發展，渦核不斷變大，直至與空腔后壁面發生碰撞變成碎片并表現出高度的不規則性。

由圖5中渦量等值線的變化歷程及圖6的渦結構情況，對空腔自激振蕩機理分析：剪切層脫落渦與空腔后壁發生碰撞產生一次壓力波，一次壓力波向空腔前緣傳播，擾動剪切層并激發剪切層更大的不穩定性，產生新的脫落渦，形成空腔自激振蕩，完成一次反饋過程。

圖6　Q指標定義的瞬時三維渦結構Fig.6 Instantaneous three-dimensional vortexstructure defined by Q criterion

在本文計算中，使用的工作站為3.0 GHz主頻、20核心的DellTMPower EdgeTMT7610。計算表明在同樣網格數目和相同邊界條件下計算300個時間推進步長，SM模型需要40 min，DSM模型和WALE模型均需要41 min。因此可以看出這些模型在計算效率上沒有明顯差異。

經過三種亞格子模型計算，各個監測點的聲壓史被記錄。由于瞬態計算的流場是一個由不穩定狀態逐步發展到準穩態的過程，最終選用經過0.1 ～0.3 s達到準穩態的215個數據進行快速傅里葉變換（FFT）。實驗采樣時間為本文FFT變換采樣時間的20倍，因此將實驗數據均分為20段，圖7中的實驗值的壓力頻譜是20段數據的整體平均。圖7將對空腔內有代表性的P1、P4、P7和P10進行重點分析。為清晰表明三種亞格子應力模型在預測空腔自激振蕩方面的差異，在P10點分別列出三種亞格子模型結果與實驗結果的對比，P1，P4和P7點處為綜合對比。

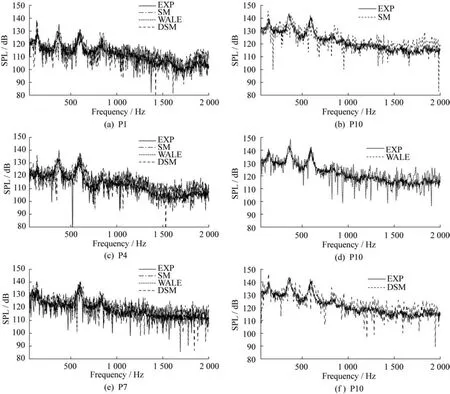
圖7　聲壓頻譜圖Fig.7 Sound pressure spectrum

三種亞格子模型的模態頻率和聲壓級與實驗值吻合良好，都在合理預測范圍之內。空腔自激振蕩能量主要集中在0～1 000 Hz的低頻區域，前三階模態頻率對應的聲壓級較大，是空腔自激振蕩的主要振蕩模式。在預測精準度上，三種亞格子模型仍有一定差異。表2、表3給出了P10點處三種亞格子模型前四階模態頻率及對應聲壓級與Rossiter公式和實驗值的對比情況，括號內數值為計算值與實驗值的相對誤差。Rossiter公式如下：

其中：fn為空腔振蕩的模態頻率，Hz；L為空腔長度，m；U∞為自由流速度；M∞為自由流馬赫數；n為模態數；κ為渦速度與自由流速度比相關的常數，κ=0.57；γ為渦通過與產生聲壓之間的時間延遲因子，Lionel Larcheveque認為γ是與空腔長寬比相關的一個常數，當L/D=5時，γ=0.29［16］。

由表2和表3可以看出，若以3%相對誤差為界限作為評價誤差大小依據，SM模型的第一、二和第四階模態頻率預測偏差較大，而WALE模型的第二階模態頻率預測準確度較低。同時，SM模型和DSM模型的第一、四階模態對應的聲壓級與實驗值差別較大。上述差異也體現在P1、P4和P7這三個點上。因此，可以看出，由于SM模型采用單一的Cs常數，不能準確模擬有剪切流的固體壁面附近流動情況；DSM模型動態計算Cs常數的方法可以有效改善這一情況；WALE模型使用了正確的固體壁面流動的漸進行為，各監測點的聲壓頻譜預測與實驗值最為接近，表明WALE模型和DSM模型在預測監測點頻率聲壓級分布方面要優于SM模型。

表2　P10點前四階模態頻率Table 2 Frequency of the first four modes at P10

表3　P10點前四階模態聲壓級Table 3 SPL of the first four modes at P10

4　結 論

本文使用SM、DSM和WALE三種亞格子模型對三維矩形空腔自激振蕩流動進行大渦數值模擬，并與實驗結果對比分析，得出以下結論：

（1）三種亞格子模型計算的前四階模態頻率與Rossiter公式計算結果和實驗數據吻合良好，空腔自激振蕩能量主要集中在0～1 000 Hz的低頻區域，前三階模態是主要的振蕩模式，空腔自激振蕩并沒有嚴格的周期性。

（2）從計算的時間效率上來看，三種亞格子模型并無顯著差異。由空腔底部監測點聲壓級分布及聲壓頻譜圖可以看出：WALE模型性能最佳，DSM模型也能給出與實驗相符合的結果，SM模型的預測性能略差。

（3）由于WALE模型在近壁區域計算的優越性，相比SM和DSM模型，能更準確地預測空腔自激振蕩的模態頻率和壓力幅值。該結果也間接說明亞格子模型對數值模擬結果的重要性。

［1］ ROSSITER J E.Wind tunnel experiments of the flow over rectangular cavities at subsonic andtransonic speeds［R］. London：Ministry of Aviation，1967：3438.

［2］ LARCHEVêQUE L，SAGAUT P，LE T H，et al.Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number［J］.Journal of Fluid Mechanics，2004，516：265-301.

［3］ GALPERIN A，ORSZAG S A.Large Eddy Simulation of Complex Engineering and Geophysical Flows［M］.USA：Cambridge University Press，1993.

［4］ SMAGORINSKY J.General circulation experiments with the primitive equations：I.The basic experiment［J］.Monthly Weather Review，1963，91（3）：99-164.

［5］ 鄧小兵.不可壓縮湍流大渦模擬研究［D］.四川綿陽：中國空氣動力研究與發展中心，2008.

［6］ GERMANO M，PIOMELLI U，MOIN P，et al.A dynamic subgrid-scale eddy viscosity model［J］.Physics of Fluids A：Fluid Dynamics，1991，3（7）：1760-1765.

［7］ MOIN P，SQUIRES K，CABOT W，et al.A dynamic subgridscale model for compressible turbulence and scalar transport ［J］.Physics of Fluids A：Fluid Dynamics，1991，3（11）：2746-2757.

［8］ 周磊，解茂昭，賈明，等.不同亞網格尺度應力模型在燃油噴霧大渦模擬中的應用［J］.內燃機學報，2011，29（1）：29-35.

［9］ NICOUD F，DUCROS F.Subgrid-scale stress modelling based on the square of the velocity gradient tensor［J］.Flow，Turbulence and Combustion，1999，62（3）：183-200.

［10］ LAI Huanxin，LUO Kai.A three-dimensional hybrid LES-acoustic analogy method for predicting open-cavity noise［J］. Flow，Turbulence and Combustion，2007，79（1）：55-82.

［11］ XU Lan，CUI Guixiang，WANG Zhishi，et al.High accurate finite volume method for large eddy simulation of complex turbulent flows［J］.International Journal of Turbo and Jet Engines，2006，23（3）：191-210.

［12］ HENSHAW M J.M219 cavity case：Verification and validation data for computational unsteady aerodynamics［R］. ［s.l.］：British Aerospace（Operations）Ltd.，2000：453-472.

［13］ PLENTOVICH E B，STALLINGS R L，TRACY M B. Experimental cavity pressure measurements at subsonic and transonic speeds［J］.NASA Technical Paper，1993，3358：1-128.

［14］ 肖紅林，羅紀生.大渦模擬中亞格子模型的改進及其在槽道湍流中的應用［J］.航空動力學報，2007，22（4）：583-587.

［15］ 賴煥新，周邵萍，羅開紅.空腔的非定常可壓縮過流及相關氣動聲學問題［J］.工程熱物理學報，2007，28（5）：755-758.

［16］ LARCHEVêQUE L，SAGAUT P，MARY I，et al.Largeeddy simulation of a compressible flow past a deep cavity［J］. Physics of Fluids，2003，15（1）：193-210.

Calculation of Oscillation Flow in Open Cavity Using Three Sub-grid Scale Models

BAI Hai-tao， LAI Huan-xin
（Key Laboratory of Pressurized Systems and Safety，Ministry of Education，East China University of Science and Technology，Shanghai 200237，China）

Three sub-grid scale models are employed to calculate the compressible fluid in a three dimensional rectangular open cavity，which has a length-to-depth ratio of 5.The frequencies of sustainedoscillation in the cavity are in agreement with experimental results and the Rossiter formula.The oscillating energy mainly concentrates on the low frequency areas.The first three modes are the basic frequencies of the flow induced oscillation.The main discrepancies of sound pressure level（SPL）occur in the areas near the fore and aft walls.The results of dynamic Smagorinsky-Lilly（DSM）model are more closer to experimental data than that of Smagorinsky-Lily（SM）model.The results of Wall Adapting Local Eddy Viscosity（WALE）model are the closest to the experimental data.The results of sound pressure level and sound pressure spectrum at the bottom of the cavity demonstrate that WALE model is the best one to predict the self-sustained oscillation of the cavity，while DSM model is fairly good，SM model is slightly inaccurate.

open cavity；self-sustained oscillation；large eddy simulation；sub-grid scale model；aerodynamic noise

O353.4

A

1006-3080（2016）01-0125-07 DOI：10.14135/j.cnki.1006-3080.2016.01.020

2015-05-08

國家自然科學基金（51576067）

白海濤（1989-），男，河南南陽人，碩士生，主要從事氣動聲學的研究。E-mail：bht119@126.com

賴煥新，E-mail：hlai@ecust.edu.cn