神經網絡的非脆弱狀態估計

楊帆 董宏麗 李佳慧 安杏杏 邵曉光

幾十年來,由于其自適應學習和逼近非線性函數的能力,遞歸神經網絡(RNNs)已經成為研究焦點.到目前為止,各種遞歸神經網絡的結構以及學習方案已經被用于分類、模式識別、回歸和優化問題及許多實際應用領域,如系統的識別和控制,軌跡預測,決策和醫療診斷[1?2].另一方面,由于電子神經網絡中放大器的有限開關速度和其他原因,通常使信號傳輸時產生時滯是不可避免的.如果沒有適當的考慮,時滯將會引起系統振蕩甚至不穩定.在過去的十年里,對于各種神經網絡和其他網絡時滯現象在動力學分析問題中得到了大量的研究關注[3?9].

對于神經網絡的成功應用,往往是先了解可用于優化或控制的神經元狀態的實際信息.然而,由于資源物理上可利用的限制,通常只有部分神經元狀態信息可通過網絡輸出,尤其是大規模神經網絡.因此,當務之急是通過可用的網絡輸出盡可能準確地估計神經元狀態[10],由此產生的神經網絡狀態估計問題在過去的幾十年中已經引起了廣泛興趣,已經有大量文章發表[11?16].例如文獻[17]中設計的狀態估計器是針對帶有馬爾可夫跳參數和時變時滯的離散神經網絡.

在控制器/估計器應用過程中,通常情況下由于各種原因,例如數值舍入誤差、計算機的有限字長和模數轉換精度,實際執行的參數與期望的會略有不同.眾所周知,即使是估計器的漂移、濾波器/控制器參數微小的變化都可能會導致整體動態系統發生巨大變化(如性能下降,甚至最終不穩定)[18?19],這種現象被稱為是脆弱的.在過去的幾年中,對于控制器/估計器在可接受的執行誤差范圍內,非脆弱性在保證所需系統性能方面已經成為一個越來越重要的性能指標[20?22].例如,文獻[22]對于一類同時帶有隨機發生增益變化(ROGVs)和信道衰落的離散T-S模糊系統,設計了一個非脆弱H∞濾波器.

在神經網絡非脆弱狀態估計的背景下,一些初步的結果已經出現在文獻中.例如,文獻[23]對于帶有混合時變時滯和馬爾可夫跳參數的神經網絡,設計了一個非脆弱觀測器.很明顯在文獻[23–24]中設計的估計器/觀測器的結構已經被假定類似于基礎神經網絡,以便隨后的動力學分析.然而這樣的假設意味著,為了估計器/觀測器的應用具有實際意義,時變時滯和激勵函數必須是完全已知的.遺憾的是,利用這種復雜的估計器/觀測器是相當不方便的,因為在參數識別和工程實現時的限制很多.因此,我們通常的想法是在保證估計性能的前提下,設計一個結構簡單、適用于實際應用的狀態估計器,這也是本文研究的主要目的.

1 問題描述

考慮如下時滯神經網絡系統:

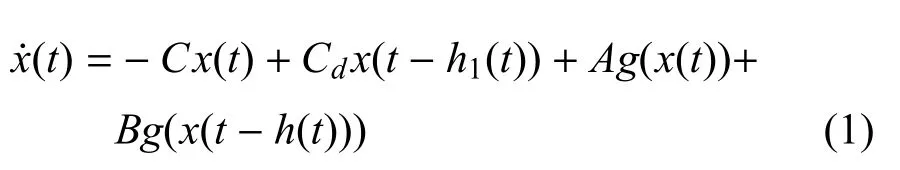
其中,x(·)=[x1(·),x2(·),···,xn(·)]T∈Rn是神經元狀態向量,g(x(·))=?g1(x1(·)),g2(x2(·)),···,gn(xn(·))?T∈Rn是初始條件為g(0)=0的非線性激勵函數,C=diag{c1,c2,...,cn}是正定對角矩陣,A,B,Cd分別是連接權矩陣、時滯連接權矩陣和常數實矩陣.h(t)和h1(t)分別是時變時滯和狀態時滯.它們滿足

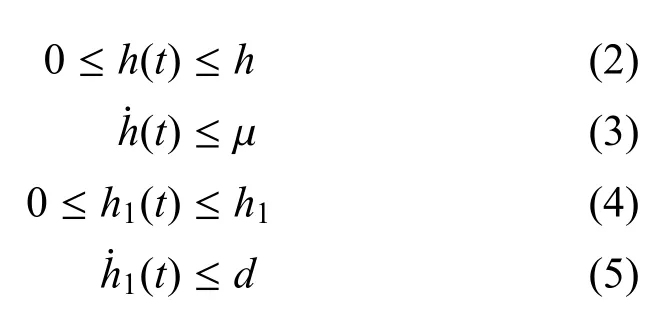
其中,h,h1,μ,d是常數.

假設1.對于任意的 α1,α2∈R,α1, α2,激勵函數g(·)滿足:

神經網絡的測量輸出表示為如下形式:

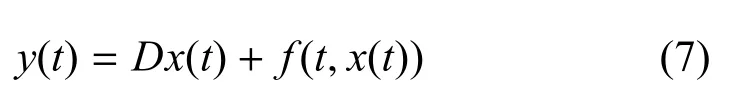
其中,y(t)∈Rm是測量輸出,D∈Rm×n是已知常數矩陣.f(t,x(t))是作用在網絡輸出的初始條件為f(0,0)=0的神經元狀態依賴非線性擾動.f(t,x(t))滿足如下的Lipschitz條件:

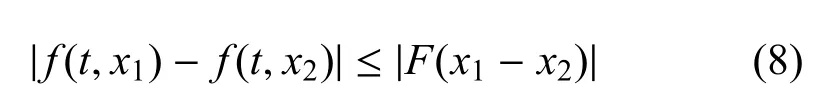
其中,F=diag{f1,f2,...,fn}是已知的常數矩陣.

全階非脆弱狀態估計器的形式如下:

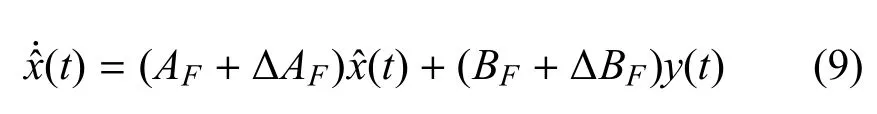
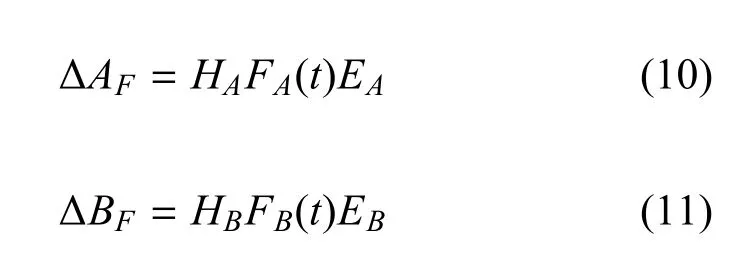
其中,HA,HB,EA和EB是已知適當維數矩陣,FA(t)和FB(t)是未知矩陣滿足和

為了便于分析,定義如下:

結合式(1)～式(7)式及式(9),可以得到如下增廣系統:

其中

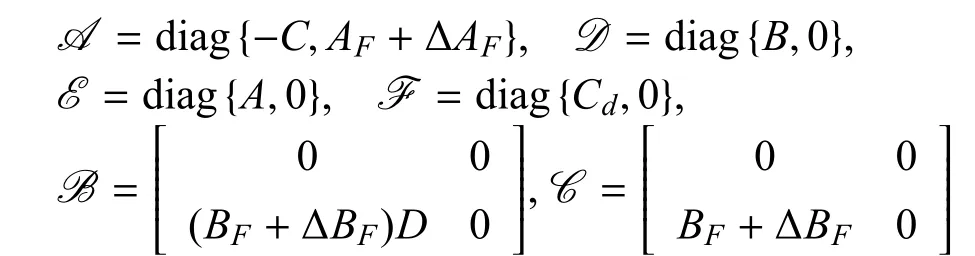
從式(6)和式(8)可以得到

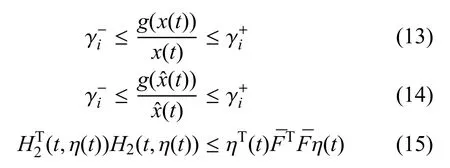
定義1.如果滿足下列式子,則增廣系統式(12)漸近穩定:

本文的目的是為連續神經網絡式(1)設計一個非脆弱估計器,使增廣系統式(12)漸近穩定.

2 主要結果

引理1[26].令M=MT,U和V是適當維數實矩陣,并且V滿足VTV≤I,只要存在一個正定標量ε使M+εUUT+ε?1WTW<0或

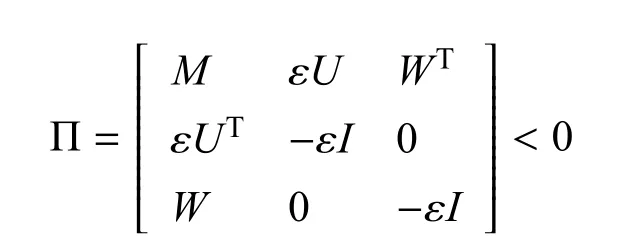
成立,則M+UVW+WTVTUT<0成立.

引理 2[2]. 假設Z= diag{β1,β2,...,βn} 是半正定對角矩陣,令x=[x1,x2,···,xn]T∈Rn,O(x)=[o1(x1),o2(x2),···,on(xn)]T是連續非線性函數且滿足

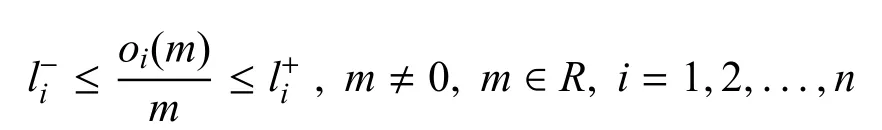
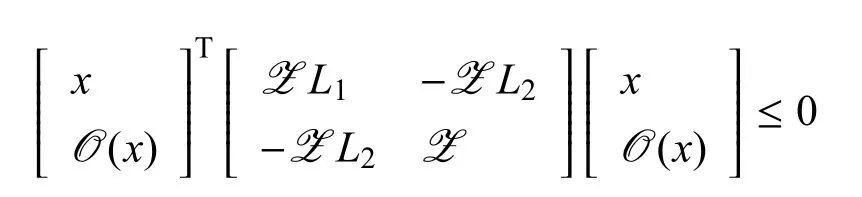
或者xTZL1x?2xTZL2O(x)+OT(x)Z O(x)≤0,其中

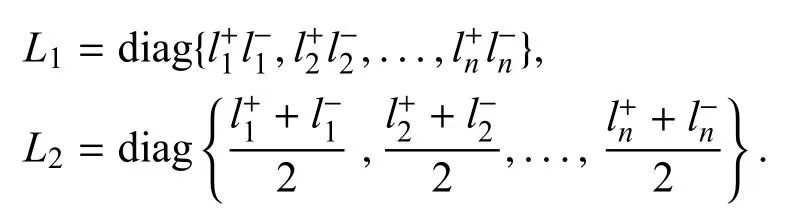
引理3[27].對于任意的正定矩陣R>0,常數h>0,如果存在向量函數x(t):[0,h]→Rn,使得積分有定義,則下面的不等式成立

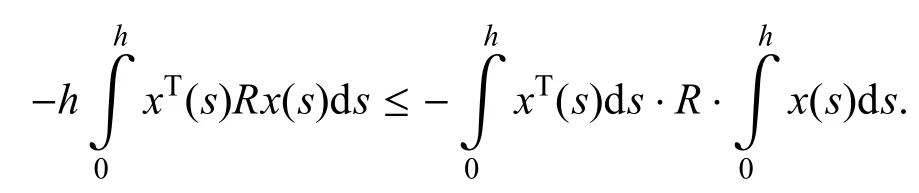
現在開始進行增廣系統式(12)的穩定性分析.

定理1.考慮連續神經網絡式(1)～式(7),其包含時變時滯,非線性擾動和增益變量.估計器參數AF和BF已知.如果存在正定矩陣P>0,K>0,矩陣正標量ε1和4個對角矩陣L>0,H>0,J>0,Y>0,滿足下列線性矩陣不等式(LMI):

則增廣系統式(12)漸近穩定,其中

證明:構建如下Lyapunov函數:

其中,V1(η(t))= ηT(t)Pη(t)

沿式 (12)的軌跡計算式 (30)中Vi(η(t))(i=1,2,...,7)的導數得(η(t))=2ηT(t)P(t)

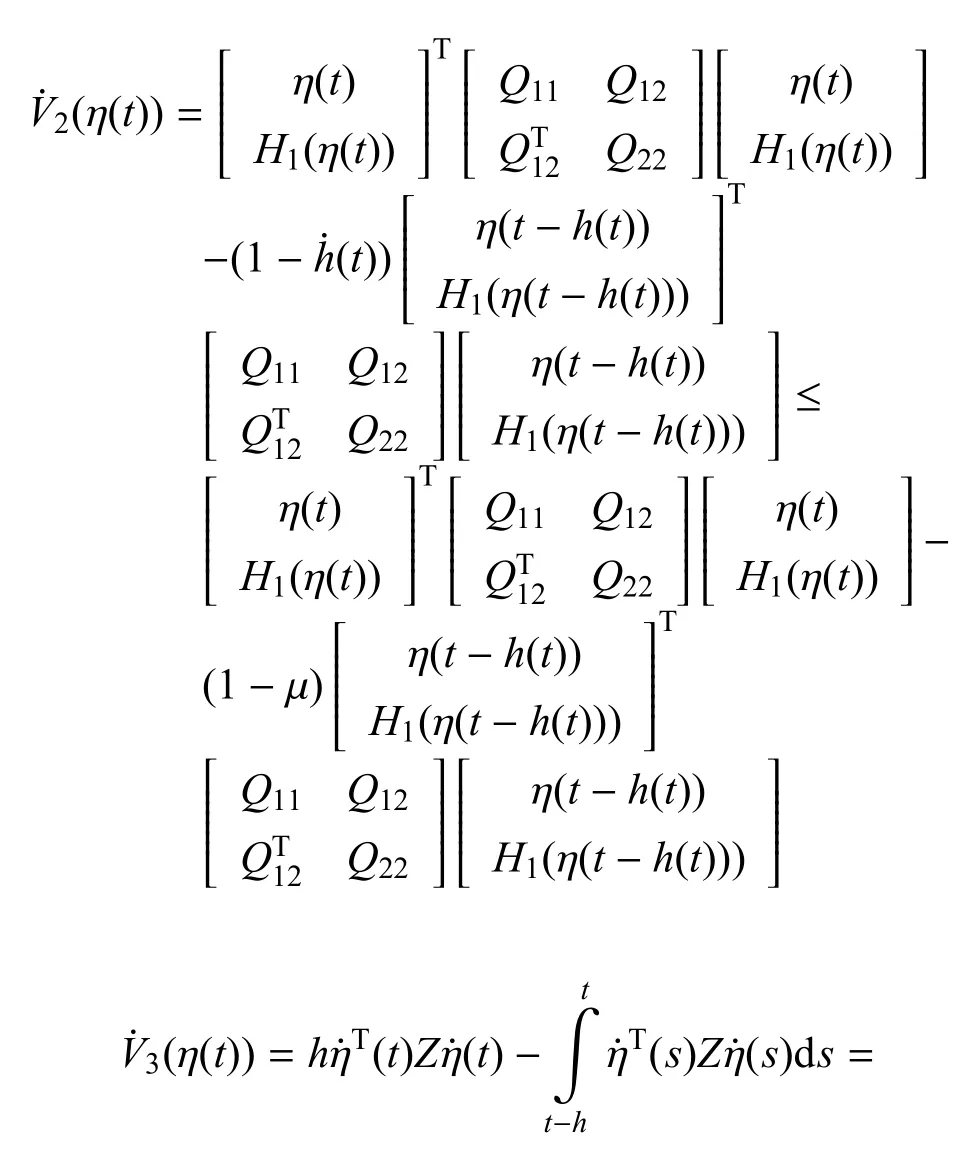
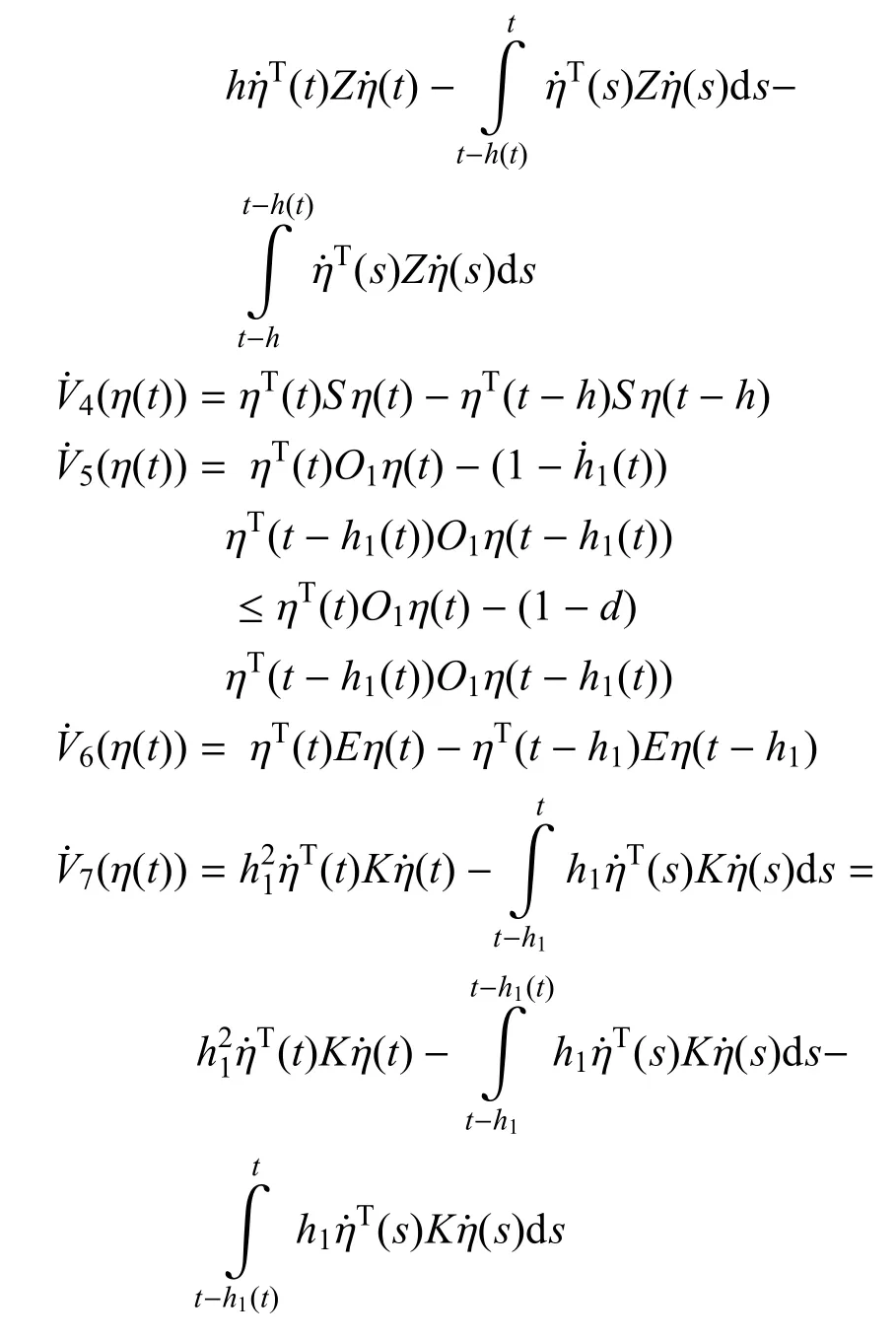
令m=h1(t)/h1,可以得到

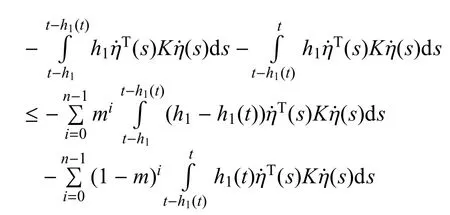
令上述不等式中n=2,同時利用引理3可以得到

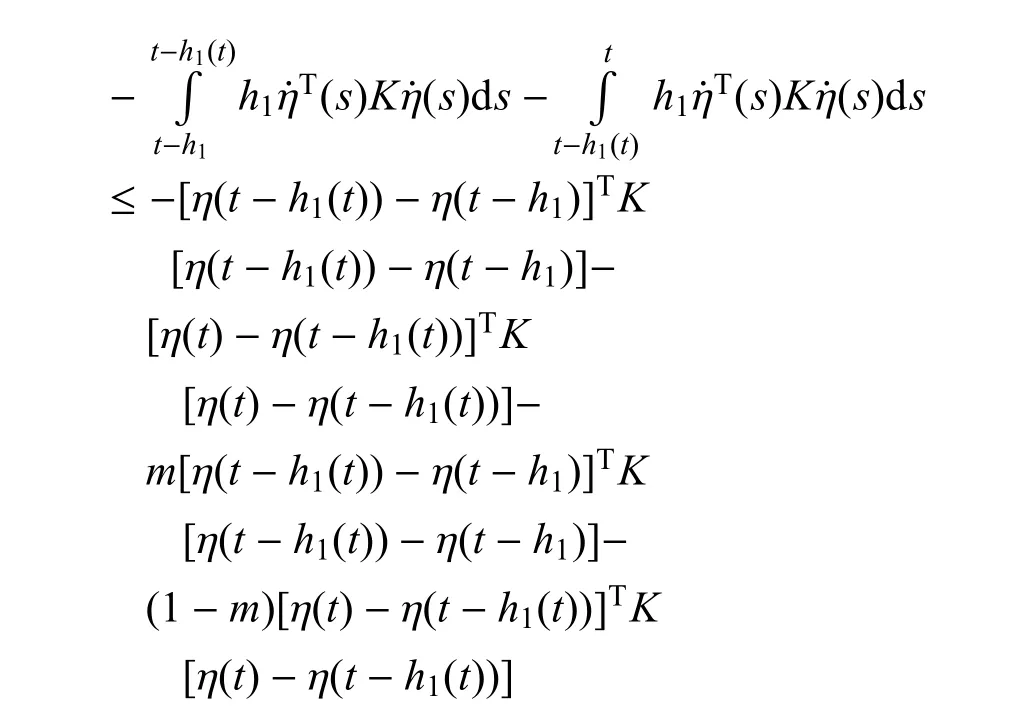
對適當維數的矩陣M和N利用Leibniz-Newton公式,可以得到如下等式:

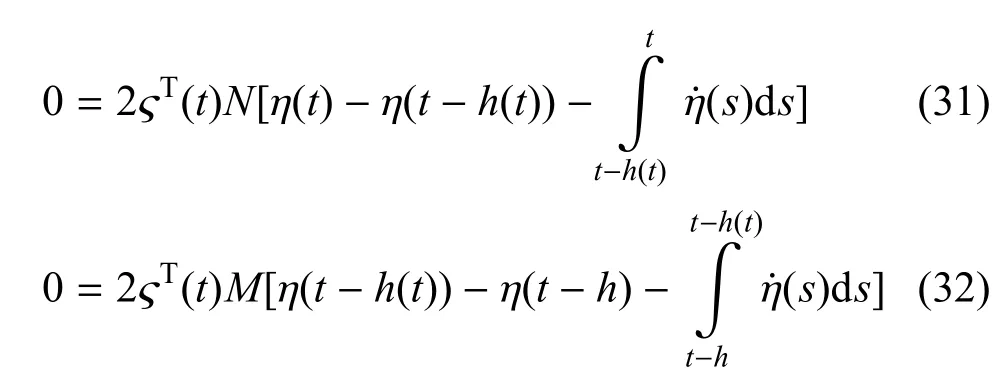
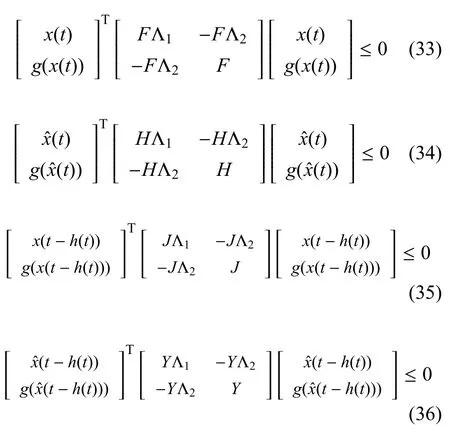
然后由假設1和引理2得到由式(33)～式(36)進一步得到

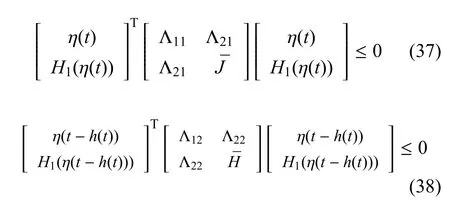
此外,根據條件式(15),對于正標量ε1推斷出

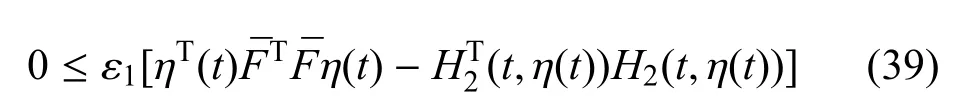
對任意適當維數的矩陣X=XT可以得到

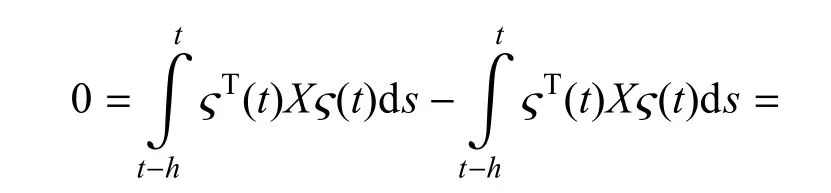
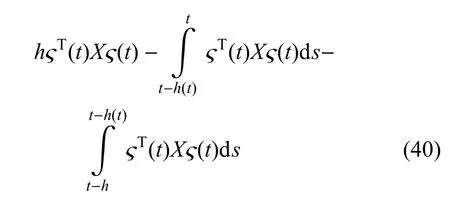
將式(31)～式(32)、式(37)～式(40)的右側加到Vi(η(t))(i=1,2,...,7)的導數中,得到

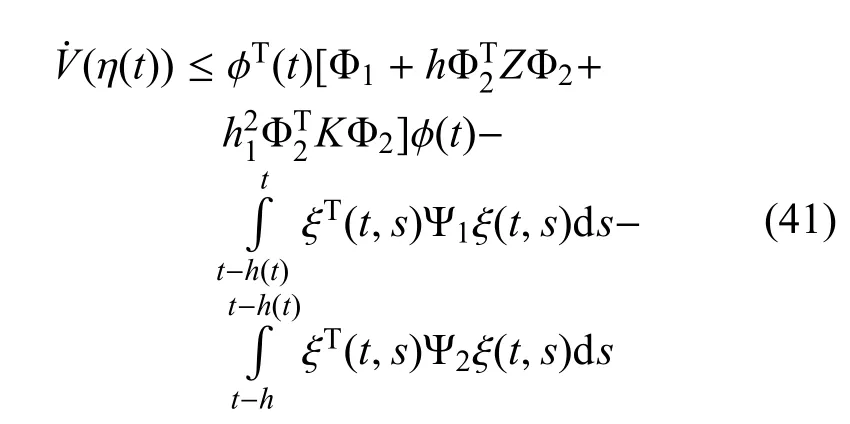
其中

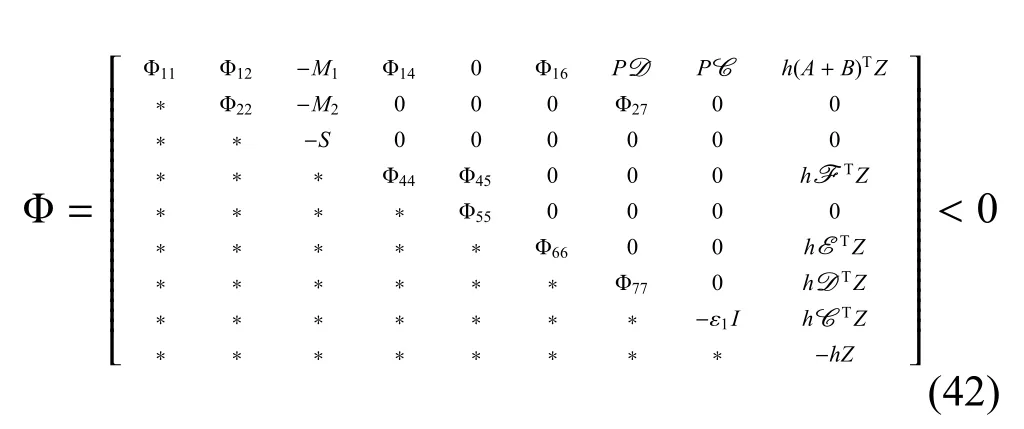
觀察到(P?Z)TZ?1(P?Z)=PZ?1P?2P+Z>0,推出PZ?1P≥2P?Z.然后由(17)式得到(43)式成立.令然后得到α0<0并且滿足下式

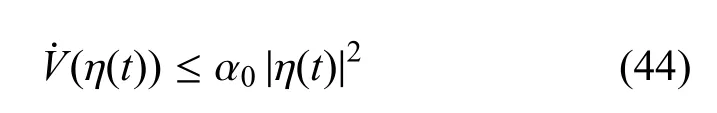
兩邊取0到T(T>0)積分,得到

因為|η(t)|2是收斂的,從而得出結論

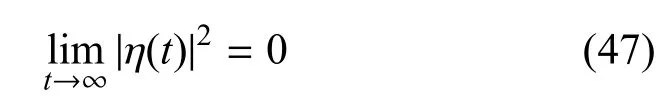
根據定理1的研究結果,下面設計時滯神經網絡系統式(1)的狀態估計器.

定理2.考慮連續神經網絡式(1)和估計器增益變量式(9).如果存在正標量ε1>0和ε>0,正定矩陣Z>0,S>0,O1>0,E>0,K>0,矩陣N=4個對角矩陣L>0,H>0,J>0,Y>0,ZA和ZB同時滿足式(18),式(19)和下面不等式:

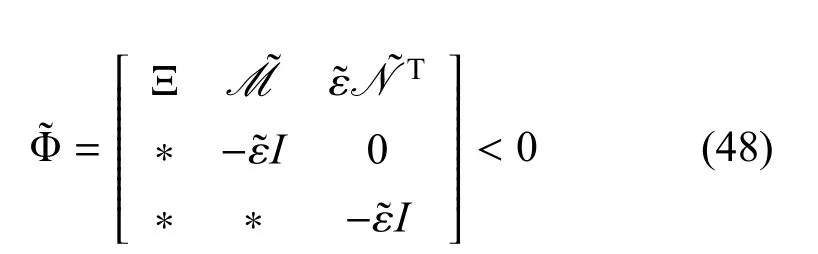
則增廣系統式(12)漸近穩定,其中

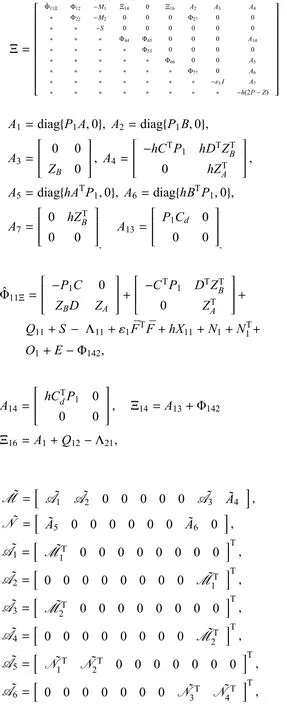
并且 Φ12,Φ22,Φ142,Φ27,Φ44,Φ45,Φ55,Φ66和Φ77分別在式(21)～式(29)式中已定義.形如式(9)的估計器增益可以通過求出.

證明:根據定理1,為了證明系統式(12)的漸近穩定性,式(48)足以代替式(17).所以用式(12)中定義的A,B,C,D,E和F代替式(17)中的?Φ,從而得到

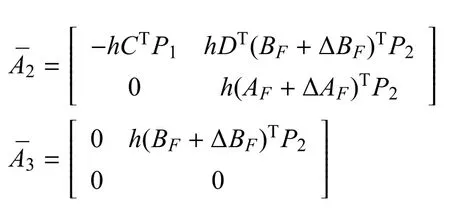
其中

另一方面令ZA=P2AF和ZB=P2BF.然后,?Ξ可被拆分成:

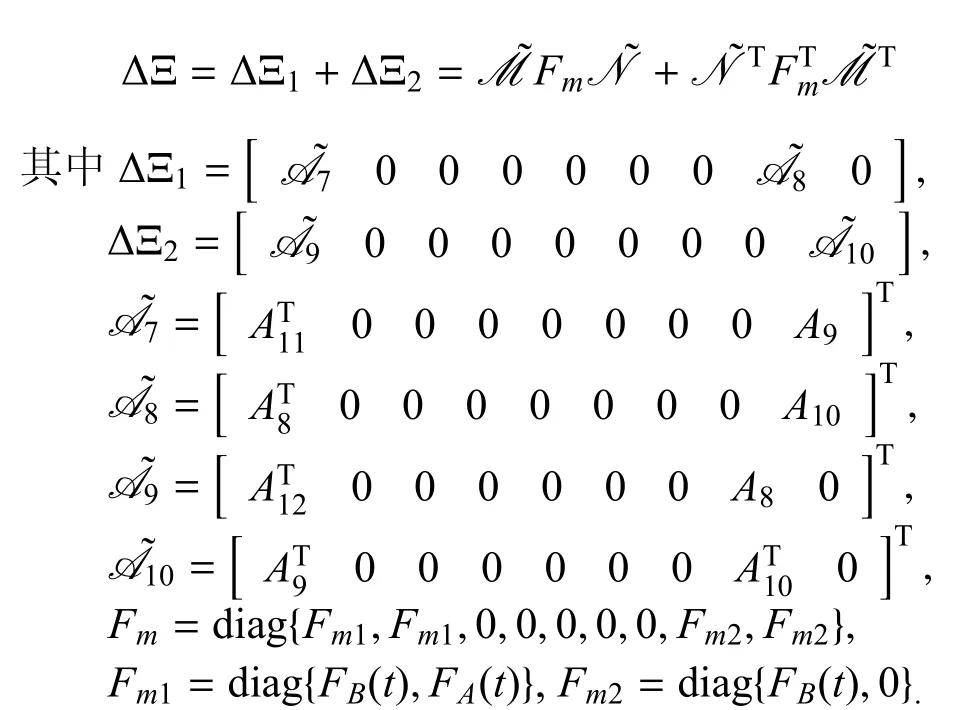
到目前為止,可以將式(17)重新寫成如下形式:

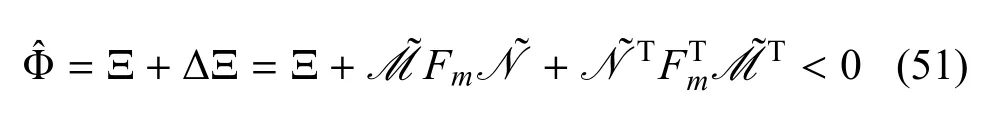
根據引理1如果存在一個正標量ε使

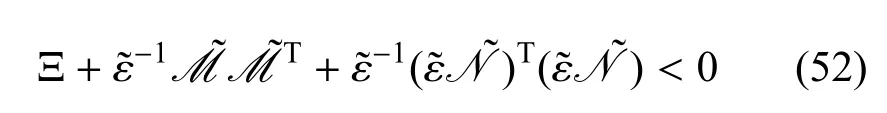
成立,則式(17)成立.根據Schur Complement引理,當且僅當式(48)成立時,式(52)成立.最后,可以得出這樣的結論:由式(48)可以得到式(17)成立,根據定理1可以得出系統式(12)漸近穩定.此外,估計器增益可以從ZA=P2AF和ZB=P2BF中求得.

注釋:定理2的研究結果中包含系統中的全部物理參數,如時滯邊界、刻畫增益不確定的矩陣等.通過求解不等式(18)、式(19)和式(48)的可行解,可以計算出期望估計器的增益.

3 數值仿真

給定時滯神經網絡系統式(1)的參數如下:

h(t)=4,h1(t)=0.5,G=0.5I.

網絡測量輸出式(7)中參數為D=I,F=0.4I,估計器增益變量中的參數為:

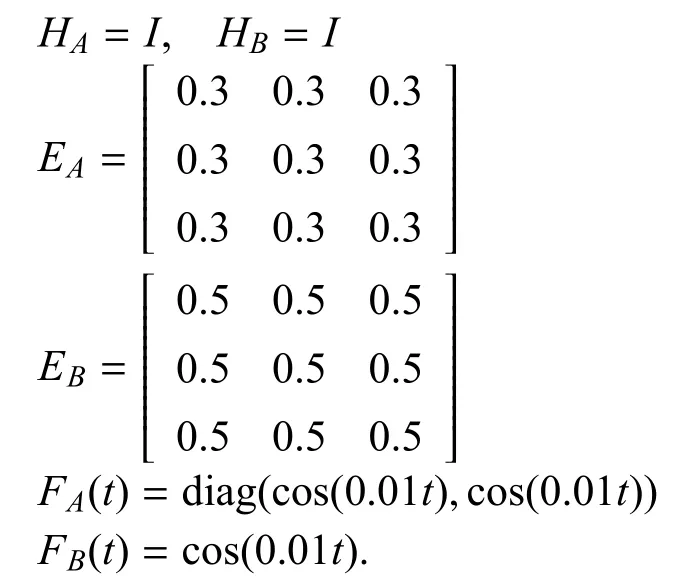
選取的激勵函數為:g1(x1(t))=?tanh(0.4x1(t))

g2(x2(t))=0.2tanh(x2(t))

g3(x3(t))=tanh(0.6x3(t))

與神經元狀態相關的非線性擾動為f(t,x(t))=0.0004cos(x(t)).

利用MATLAB軟件,經過運算,求解出估計器增益矩陣如下:

仿真結果如圖1～圖4.圖1～圖3分別描述的是神經網絡的狀態向量x1(t),x2(t),x3(t)和它們的估計向量x1(t),x2(t),x3(t).圖4描述的是狀態向量與估計向量之間的誤差.通過仿真結果驗證了增廣系統的漸近穩定性.

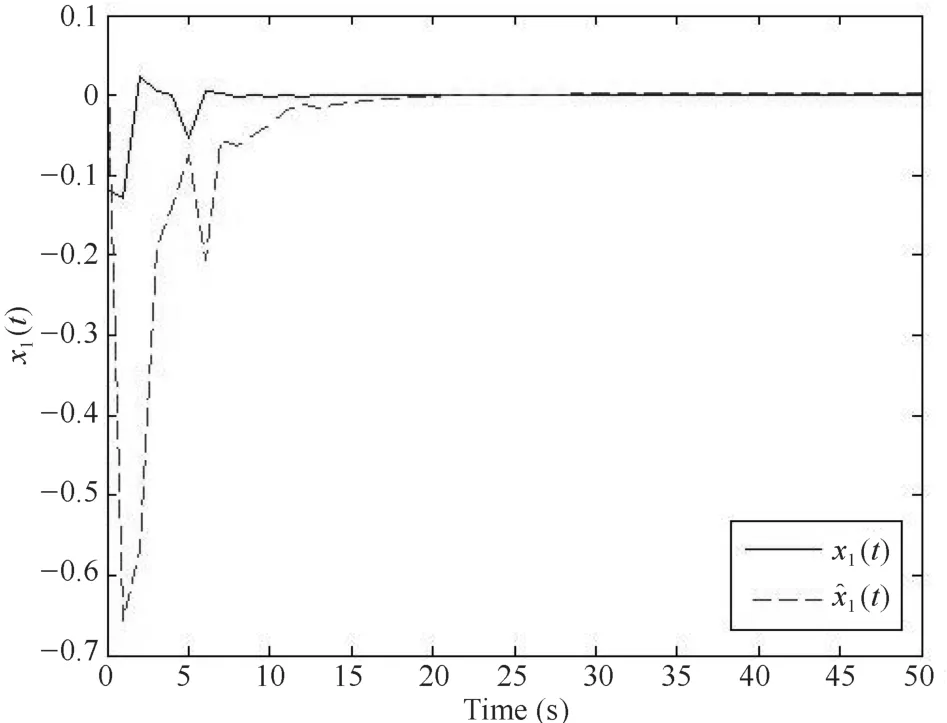
圖1 狀態向量x1(t)和它的估計x1(t)

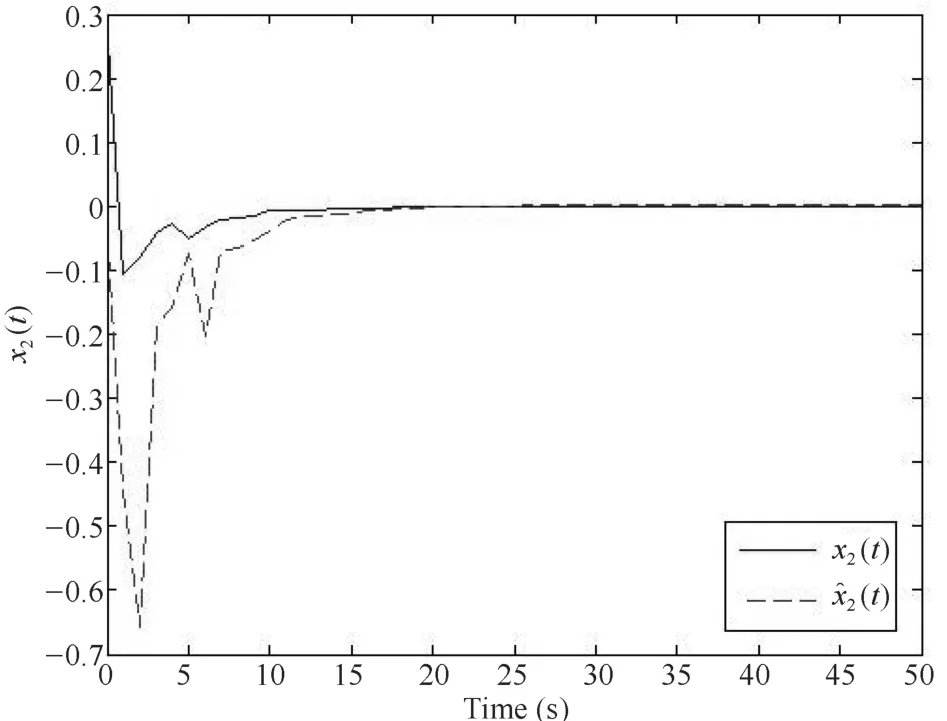
圖2 狀態向量x2(t)和它的估計x2(t)

4 結論

本文研究了帶時變時滯和非線性擾動的神經網絡的狀態估計問題.通過李雅普諾夫穩定性理論和求解幾個LMI得到估計器增益矩陣,進而得出保證增廣系統漸近穩定的充分條件.最后通過數值仿真證明了該方法的有效性.值得期待的是我們的主要結論可以推廣到更普遍或實際的系統中,例如It?o型隨機系統[28],非線性馬爾可夫跳系統[29?30],航天器姿態控制系統[31],不確定隨機系統[32],采樣數據系統[33],有限時域非線性系統[34?35],并且在不久的將來會出現與其相應的結果.此外,這里的方法可以進一步處理故障檢測問題[36],以及更復雜的神經網絡非脆弱狀態估計問題,如具有測量衰減[37?39]和不完全測量[40?41]的神經網絡.

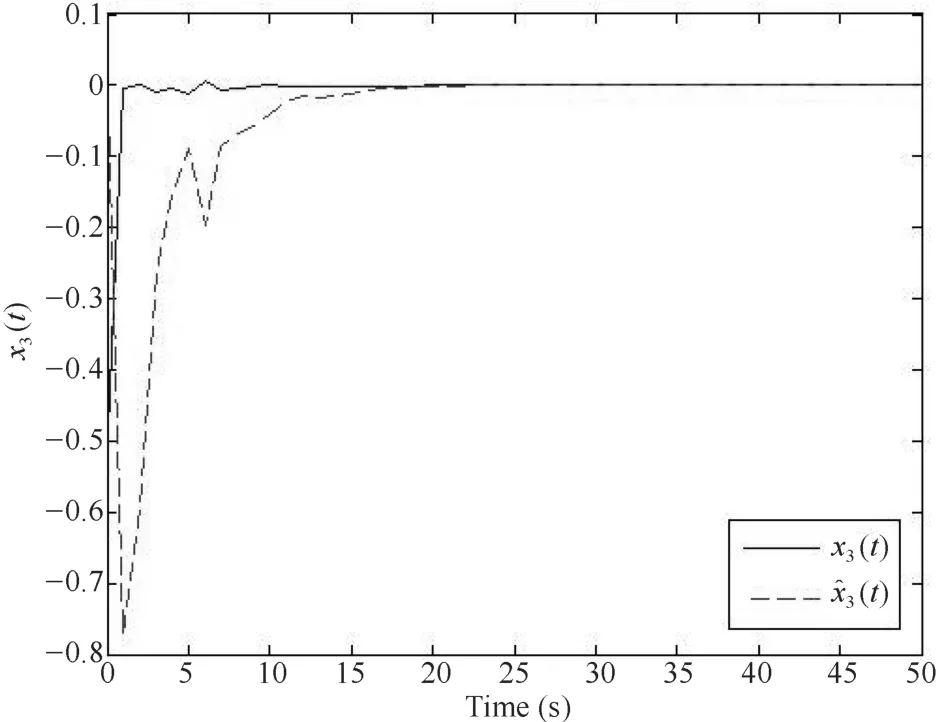
圖3 狀態向量x3(t)和它的估計x3(t)

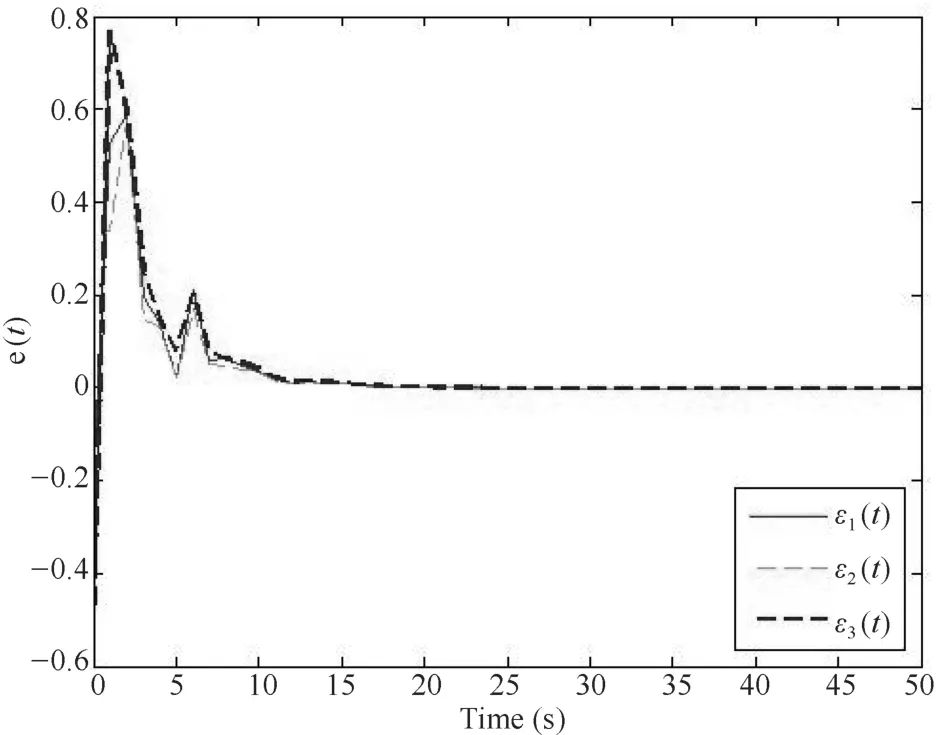
圖4 狀態向量和它的估計之間的誤差