品味楔形幾何體　感悟數學真善美*——2016年全國數學高考理科Ⅰ卷立體幾何題解法、評析及思考

●耿合眾

(潁上第一中學　安徽阜陽　236200)

?

品味楔形幾何體感悟數學真善美*
——2016年全國數學高考理科Ⅰ卷立體幾何題解法、評析及思考

●耿合眾

(潁上第一中學安徽阜陽236200)

文章對一道高考數學試題的解法進行探究，試圖從外在的形式中多角度尋找數學的本源性東西，在評析過程中思考：什么是學習數學的本質；在進行數學教學時，數學的核心素養的立足點在哪兒.借助對數學問題的品味，感悟數學試題中蘊涵的真善美.

楔形幾何體;解法探究;核心素養;真善美

2016年的高考是許多省市從自主命題到統一命題的第1年，筆者所在安徽省使用的是全國Ⅰ卷(即乙卷).縱觀理科數學試卷，給人的印象是平穩大氣，結構合理,既有內容的真，也有結構的善，更有形式的美，真正體現了能力立意.試題從多方面承載了中學數學的核心價值，多角度對考生的核心素養進行考查，綜合檢驗了考生對數學知識的理解、對數學技能方法的掌握、對數學思想方法的感悟和對數學活動經驗的積累.

下面以理科Ⅰ卷立體幾何題為例，重溫該題的解法探究歷程，在簡單評析里品味數學的核心內容，從而感悟數學的真善美.

1　試題再現

圖1

題目如圖1，在以A，B，C，D，E，F為頂點的五面體中，面ABEF為正方形，AF=2FD,∠AFD=90°，且二面角D-AF-E與二面角C-BE-F都是60°.

1)證明：平面ABEF⊥平面EFDC；

2)求二面角E-BC-A的余弦值.

(2016年全國數學高考理科Ⅰ卷第18題)

2　楔形幾何體

該題以一個五面體為載體，考查面面垂直的證明和二面角大小的求解.該幾何體底面為正方形，頂部為平行于底面的一條線段，4個側面中有2個是梯形，另2個是三角形，這樣的多面體好像木工用的楔，通常稱此種幾何體為楔形.著名的楔形文字就是因為每一筆畫總是由粗到細，像木楔一樣而得名.楔形幾何體又可看作是三棱柱按對稱切割2個小三棱錐后得到的結果.從這個角度來看，該試題是來自生活中的數學，體現了數學中的生活實際，取材于課本中人們熟悉的幾何體進行切割.在試題的表現形式上充分體現數學的真善美.

3　問題解決

數學問題的解決，體現了對數學問題本質的理解.用數學的眼光觀察問題，用數學的思維分析問題，用數學的語言表達問題.在立體幾何中，數學核心素養的五大基本能力(抽象概括、邏輯推理、空間想象、運算求解、數據處理)在該題中的體現尤為突出.

3.1第1)小題，牛刀小試

垂直關系是立體幾何的重點內容，絕大多數立體幾何問題都與垂直有關，因此垂直關系也成了立體幾何的關鍵.抓住垂直就抓住了立體幾何的本質，這話一點不假.第1)小題考查的是面面垂直，自然去想面面垂直的判定定理，從而去找線面垂直，而線面垂直的本質是線線垂直，根據有關垂直關系的定理，把邏輯推理和空間想象用數學符號表達出來，就可以完成證明.

證明由面ABEF為正方形，得

AF⊥FE,

又

∠AFD=90°，

得

AF⊥FD.

在平面EFDC中，FE∩FD=F，AF⊥平面EFDC,AF?平面ABEF，從而平面ABEF⊥平面EFDC.

3.2第2)小題，漸入佳境

二面角一直是立體幾何考查偏愛的一個知識點，每年都會受到命題者的青睞.在這里表面上是計算二面角的余弦值，實際上把考查空間想象、邏輯推理與數據處理、運算求解等融匯在一起，解決的途徑不僅可以采用傳統的幾何法，還可以用向量法.然而其根本是對楔形幾何本質特征的理解和思考.

圖2

解法1如圖2，由面ABEF為正方形，知

AB∥EF,

從而AB∥平面EFDC,

因此

AB∥CD，

即

EF∥CD.

又因為二面角D-AF-E與二面角C-BE-F都是60°，且AF⊥平面EFDC，AF∥BE,所以

∠DFE=∠CEF=60°，

從而四邊形是等腰梯形，將其補成矩形EFMN.聯結MA，MF，NB，NE，易得MAF-NBE為直三棱柱.

平面NBE⊥平面ABNM，交線為BN，在平面NBE中，作EH⊥BN，垂足為H.在平面ABNM中，過點H作HG⊥BC，垂足為G，聯結EG，易得EG⊥BC,于是∠HGE是二面角E-BC-N的平面角，而二面角E-BC-N與二面角E-BC-A互補，因此二面角E-BC-A的余弦值是∠HGE余弦值的相反數.又AF=2FD，設FD=1=CE，AF=2=BE，且BE⊥平面EFMN,得

在Rt△NEB中，

在Rt△CEB中，

在Rt△EHG中，

評注該解法立足于楔形幾何體的本質特征，還原切割前直三棱柱的本來模樣，充分體現轉化和化歸思想.解題，就是退，退到不能再退的時候，問題的本源也就清楚了.

圖3

于是

評注該解法把問題回歸到長方體之中.長方體是立體幾何最重要的載體之一，很多幾何體都可以補全為長方體，使得相應的證明和計算都更為清晰和容易，也更能弄清空間點線面的位置關系和數量關系.

解法3由解法1知

∠DFE=∠CEF=60°.

由AB∥EF，AB?平面EFDC，EF?平面EFDC，知AB∥平面ABCD,AB?平面ABCD，且平面ABCD∩平面EFDC=CD，于是

AB∥CD，

從而

CD∥EF，

知四邊形EFDC為等腰梯形，可得

∠CDF=∠DCE=120°,DC=DF,

∠DCF=30°,∠FCE=90°,

即FC⊥CE.又EB⊥平面EFHG,CF?平面EFHG，則CF⊥EB，故CF⊥平面CEB，得平面CFB⊥平面CEB.

在平面FHA內過點F作FM⊥AH交AH于點M，則FM⊥平面CBA.由CF⊥CB，則∠FCM是二面角F-BC-A的平面角，設其為α.又由題設EF=EB=2，EC=1，知

得

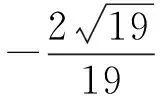
評注該解法把所求二面角分成一個直二面角和一個銳二面角的和，而其中銳二面角大小比較容易求解，這也是求鈍二面角常見的方法之一.

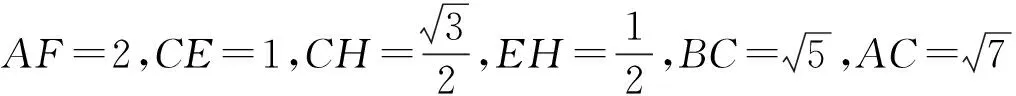
由題意知θ為鈍角，故

評注該解法回避了找二面角平面角的過程，有時二面角的問題難就難在“找”和“證”上.在一個半平面里選一點，求出該點到另一個半平面的距離和到二面角棱的距離，就可以去求二面角平面角的正弦值了，而這2個距離，利用等體積和等面積就能輕松確定.

解法5由解法1知

∠DFE=∠CEF=60°.

由AB∥平面CEF，得AB∥CD，EF∥CD，易得四邊形CDEF與四邊形ABEF均為等腰梯形.如圖4，過點A作AH⊥BC于點H，過點H作HP⊥BC交BE于點P，則∠AHP為二面角E-BC-A的平面角.令DF=1，則

過點C作CO⊥AB于點O，則

由△BHP∽△BEC得

在△AHP中，由余弦定理得

評注解法5先選取與二面角的2個半平面都相交的一個平面α，在二面角的一個半平面與平面α的交線上選一點向二面角的棱作垂線，再由該垂足在二面角的另一個半平面內作二面角棱的垂線，與平面α的交線交于一點，這2條垂線形成的角就是二面角的平面角，求出剛才3個點組成的三角形3條邊長，利用余弦定理即可獲解.

圖4 圖5

解法6如圖5，由面ABEF為正方形，得

AB∥EF，

從而

AB∥平面EFDC，

因此

AB∥CD，

即

EF∥CD.

又二面角D-AF-E與二面角C-BE-F都是60°，且AF⊥平面EFDC，AF∥BE，得

∠DFE=∠CEF=60°,

則四邊形EFDC和四邊形ABCD都是等腰梯形.

由AF=2FD，設FD=1=CE，AF=2=BE，且BE⊥平面EFMN，CD=1,于是在Rt△CEB中，作EH⊥BC，垂足為H，則

從而

即

解得

評注該解法從二面角中選擇以二面角的棱為公共邊的2個三角形，分別從二面角的棱外三角形頂點向棱作垂線，根據所給出的條件，利用解三角形知識求出相關線段的長.再利用向量夾角和二面角大小關系，由向量回路尋找等式，借助向量的模長和數量積得出二面角余弦值的關系式.

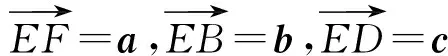
記平面EBC的一個法向量為

n1=xa+yb+zc，

令x=1，z=-1，則n1=a-c.記平面ABC的一個法向量為

n2=xa+yb+zc，

令x=4，y=-3，z=-16，則

n2=4a-3b-16c.

因為

n1·n2=12，

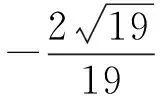
評注該解法是向量法的一種——基向量法，這種解法容易被忽視.只要在幾何體中找到從一點出發的3條線段的長度和夾角，就可以選定為空間向量的一個基底，剩下的就是數據計算的事了.

解法8由第1)小題知

∠DFE=∠CEF=60°,

因為AB∥EF，AB?平面EFDC，EF?平面EFDC，所以AB∥平面EFDC.又AB?平面ABCD,平面ABCD∩平面EFDC=CD,則AB∥CD，從而CD∥EF，四邊形EFDC為等腰梯形，且平面ABEF⊥平面EFDC.

圖6

建立如圖6所示的空間直角坐標系E-xyz.

得

y1=0,

z1=-1,

即

得

x2=0,

設二面角E-BC-A的大小為θ，則

評注坐標法主要是利用向量的相關知識及其運算來解決問題，即用代數的方法解決幾何問題.將形轉化為數來解決，降低了立體幾何的思維難度，解題思路有一定的規律性，便于學生掌握.但尋找并判斷從一點出發的3條兩兩垂直的直線是重點，也是難點.

4　一些思考

今后將有更多的省市加入全國卷統一命題的行列，對全國卷進行評析和思考是一件有價值和有意義的事情.而對全國卷的適應及思路的調整將是一個必然的過程，全國卷的試題更加體現命題的“能力立意”這一原則，更能深入到數學的本質，更能體現數學的意蘊，并且對數學核心素養的形成和培養目的非常明確.

說到數學核心素養，離不開數學的學習、應用和創新.綜合體現在發現與提出問題、分析與解決問題的過程之中.數學知識是高度抽象的，它的語言(特別是數學符號、圖表語言)是高度概括、凝練的.正是這種高度的抽象性才使數學成為連接現實世界與人類智慧的橋梁，使數學語言成為表達客觀世界結構的唯一精準語言.立體幾何正緊緊圍繞“數量關系”“空間形式”“數形結合”和“公理化思想”這4條主線，讓學生有機會體會和認識一些數學本源性問題.對立體幾何問題的解決，傳統幾何法的角度，現代向量或向量坐標法的途徑都是對該類問題本質的考量，空間想象能力、邏輯思維能力、推理論證能力、數據處理能力和運算求解能力都也是對數和形這兩大關系的深刻理解.

在今后的數學教學中，不僅要緊緊抓住對基礎知識、基本技能的掌握，還要重點提高對數學思想方法和數學本質的理解，更重要的是培養學生繼續學習的潛能，從而努力實現數學核心素養的形成和促進人的發展.最終在品味數學的過程中，充分感悟數學的真善美.

16-06-27；

2016-07-27

耿合眾(1974-)，男，安徽潁上人，中學高級教師.研究方向：數學教育.

O123.2

A

1003-6407(2016)10-42-05