淺談利用功能關系求做功題型

周曉強

（甘肅省敦煌市敦煌中學）

淺談利用功能關系求做功題型

周曉強

（甘肅省敦煌市敦煌中學）

一個物體能對外做功，我們認為這個物體具有能量。功和能是兩個密切相關的物理量，做了多少功就有多少能量轉化，功是能量轉化的量度。在能量轉化過程中，功扮演了重要的角色，利用功能關系求做功是高中物理教學的重點和難點之一。各種能量的轉化過程必然對應某種力在做功。高中階段常見的功能關系有：

1.合力做功與動能關系；

2.重力做功與重力勢能關系；

3.彈力做功與彈性勢能關系；

4.除重力、彈力以外其他力做功與機械能關系；

5.摩擦力做功與內能的關系；

6.電場力做功與電勢能關系；

7.利用熱力學第一定律求系統與外界之間的做功問題；

8.感應電流所受安培力做功與回路中產生電能的關系問題等等。

下面以例題的形式介紹利用功能關系求功：

一、利用動能定理求功

動能定理：合外力做功與物體動能的變化量相等，即W合=ΔEK。

動能定理與一個過程相對應，首先確定對象分析受力，其次針對過程求總功，確定初、末動能，按照定理列方程。功求解過程中涉及的位移參照物和初、末動能中速度的參照物是一致的，一般都是地面。

例1.一質量為m的小球，用長為L的輕繩懸掛在O點。小球在水平力F作用下，從平衡位置P點很緩慢地移動到Q點，如圖所示，求力F做的功為（）

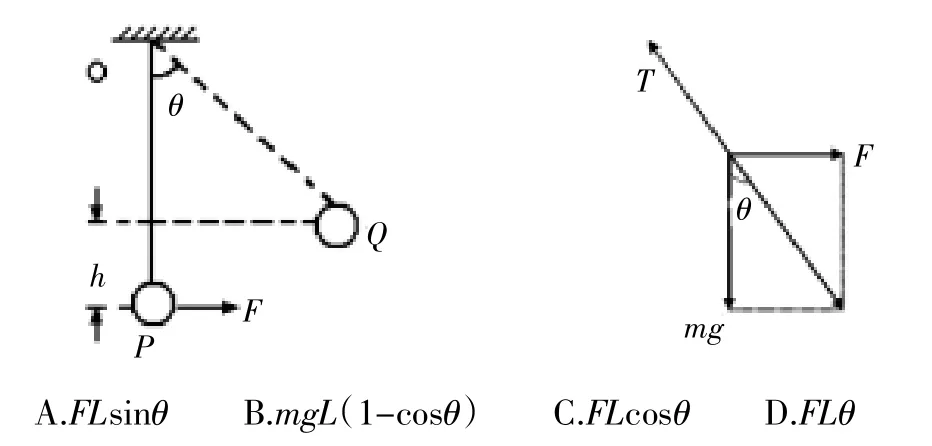
解析：對緩慢移動要抓住兩層意思：（1）物體動能不變（2）物體時刻處于平衡態。由受力分析知F=mgtanθ，F隨θ角變化，F為變力，不能用恒力做功公式。由動能定理總功為零，因此WF+WG=0，將變力做功轉化為恒力做功，WF=mgL（1-cosθ），故B正確，可見動能定理可以求變力做功問題。

說明：動能定理是一個適用面非常廣的定理，凡是涉及力對物體做功引起物體動能變化的過程幾乎都能用，既能解決恒力做功問題，又能解決變力做功問題。

二、利用重力勢能變化求重力做功

重力做正功，重力勢能減小；重力做負功，重力勢能增加。重力做功與路徑無關，只與初末位置的高度有關，重力做功等于重力勢能的改變量，即WG=-ΔEP。重力勢能是相對量，必須選參考面，默認地面。

例2.如圖所示，長度為L，質量為m的均勻繩，半段置于水平的光滑桌面上，另半段垂于桌面下，當繩下滑全部離開桌面時，則重力所做的功為多少？

三、利用彈性勢能的變化求彈力做功

彈力做正功，彈性勢能減小，彈力做負功，彈性勢能增加。彈力做功等于彈性勢能的改變量，即W彈=ΔEp彈。

例3.如圖所示，質量為m的物體從固定的光滑斜面上的A點由靜止滑下，與固連在斜面上并且沿斜面方向的輕質彈簧接觸，并將彈簧壓縮至最低點B，試求彈簧對物體做的功。（已知AB=x，斜面傾角為θ，彈簧原長在A點）

解析：以彈簧、物體為系統，由機械能守恒定律：初末位置動能為零，重力勢能轉化為彈性勢能，即：ΔEP重減=ΔEP彈增=mgxsinθ，由彈簧彈力做功與彈性勢能的關系得：W彈-ΔEP彈=-mgxsinθ，彈力做了等量負功。

說明：此題也可以應用動能定理求得。

四、除重力、彈力以外其他力做功與機械能的關系

由動能定理W合=ΔEK將總功一分為二，將重力（或彈力）做功與其余的力做功分開，W其他+WG=ΔEK，又WG=-ΔEP將其代入，W其他=ΔEK+ΔEP=ΔE，即除重力（或彈力）之外其他力做功等于機械能的增加量，其他力做正功，機械能增加，其他力做負功，機械能減小。我們平時所見的多數過程機械能并不守恒，這就可以利用機械能的變化求其他力做功。

例4.如圖所示，電梯的地板上放一質量為m的物體，鋼繩拉電梯由靜止開始以加速度a向上勻加速運動，當上升的高度為h時，物體的機械能增加了多少？

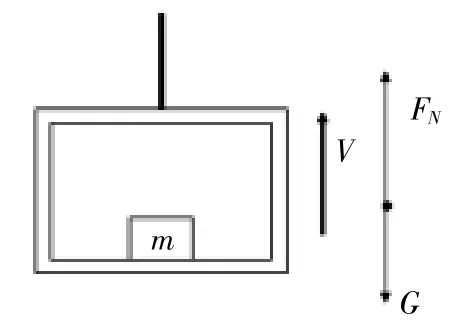
解析：對物體受力分析知，除重力之外，物體受支持力FN，支持力做正功，物體機械能增加，由牛頓第二定律FN-mg=ma，FN= mg+ma，W其他=ENh=（mg+ma）h，即物體機械能增加了（mg+ma）h。

五、摩擦力做功與內能的關系

摩擦力做功的特點：

1.無論靜摩擦力還是滑動摩擦力，都可能做正功、負功或不做功；

2.一對靜摩擦力做功之和為零，但一對滑動摩擦力做功之和一定為負值，一對滑動摩擦力做功會使系統機械能減少轉化為內能；

3.如果只有滑動摩擦力做功，滑動摩擦力與相互作用物體相對位移的乘積等于系統機械能的損失。

例5.如圖，質量為m的子彈以速度v1射入以速度v2同方向運動的木塊，質量為M，當子彈進入木塊的深度為d時，子彈的速度為v1′，木塊的速度為v2′，若子彈與木塊之間的相互作用力恒為f，求該過程損失的機械能？

解析：設木塊的位移為s，子彈相對木塊的位移為d，相對地面的位移為（s+d）

兩式相加：

說明：由上式知系統損失的動能等于滑動摩擦力與相對位移的乘積，這一結論可以應用于類似系統的動能變化之中。

六、電勢能變化與電場力做功的關系

由電場力做功定義式W電=Uabq=（φa-φb）q=Epa-Epb=-ΔEp，即電場力做正功，電勢能減小，電場力做負功，電勢能增加。

例6.電子質量為m，電量為e，沿電場線方向射入勻強電場中，電子經過A點時速率為v，到達B點的速率為零，則A、B兩點的電勢差為（）

解析：由動能定理：UA（B-e）=0-mv2，則UAB=，應選A，電場力做負功，電子在電場中的電勢能增加了。

七、利用熱力學第一定律求做功

物體通過兩種方式改變內能：做功和熱傳遞。外界對物體做功且物體吸收熱量，物體內能增加，反之，內能減少。表達式：ΔU= Q+W

例7.空氣壓縮機在一次壓縮空氣中，空氣放出熱量3×105J，空氣內能增加了2×105J，求壓縮機對空氣做了多少功？

解析：由熱力學第一定律：ΔU=Q+W得：W=ΔU-Q=2×105J-（-3×105J）=5×105J，所以，此過程壓縮機對空氣做功5×105J。

說明：應用此公式需注意物理量的正負，內能增加，ΔU為正，內能減小，ΔU為負；物體吸熱，Q為正，物體放熱，Q為負；外界對物體做功，W為正；物體對外做功，W為負。

八、在電磁感應現象中，感應電流所受安培力做功的數值與回路中產生電能的關系

安培力做正功，將電能轉化為其他形式能；安培力做負功，將其他形式能轉化為電能。感應電流的安培力做了多少功就有多少電能改變。

例8.如圖所示，有一水平的勻強磁場（磁場的方向指向讀者），在垂直于磁場方向的豎直面內放一矩形金屬框，框的一邊ab可無摩擦地上下滑動（滑動時ab仍保持水平），ab邊的質量m=2×10-4kg，長度L=0.1m，ab邊的電阻R=0.2Ω（框的其他三邊的電阻可忽略），磁感應強度B=0.1T，重力加速度g=10m/s2，空氣阻力不計，如果ab邊勻速下落，求：

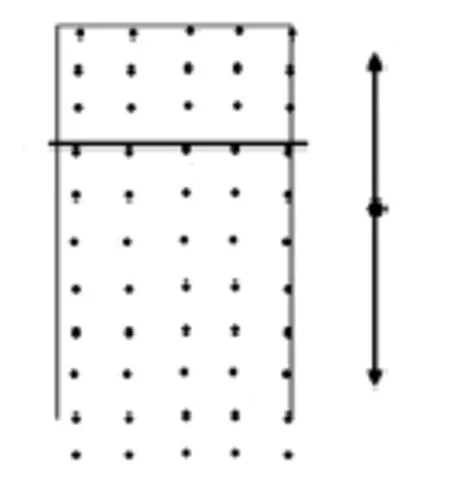
（1）ab下落的速度大小；

（2）在1s內回路中電流做的功。

解析：金屬桿勻速下落，受平衡力作用F=mg（1）

由F=BIL（2）

又感應電動勢E=BLv（3）

由閉合電路歐姆定律：E=IR（4）

解得：v=4m/s

在1s內回路中電流所做功等于該段時間內回路產生的電能。回路中產生的電能等于克服安培力做功，通過安培力做負功，機械能向電能轉化。安培力做功WF=-F×L=-Fvt=-8×10-3J。即電流所做功為W=8×10-3J。

說明：電流所做的功也等于該過程回路中產生的熱量：Q= I2Rt=8×10-3J。

總之，功是一個過程量，能量是一個狀態量，功能關系顯然將一個過程量的計算與一個狀態量的計算聯系了起來。在高考物理試題中，無論是選擇題還是計算題都會頻繁涉及功能關系，熟練掌握功能關系意味著高考的一個難點得以突破。

張小軍.高三物理“功與能”專題復習策略［J］.學周刊，2013（34）.

·編輯楊國蓉