面向兵棋推演的HPF行為動力學模型仿真實現與模型改進

張宇 柳少軍 劉洋

1.國防大學信息作戰與指揮訓練教研部北京100091

基于對人類行為實證數據的分析,運用數學、系統科學、統計學和非線性科學等理論,研究紛繁復雜的人類行為的特征、規律與動力機制,是行為動力學中一個重要的研究內容,對于研究經濟、政治、軍事等眾多社會學類學科具有重要意義.近年來,隨著計算機仿真技術的不斷發展,目前我軍大型兵棋系統已基本實現了對戰爭全要素、全過程的模擬仿真,兵棋推演已經逐漸成為我軍模擬訓練和研究作戰問題的重要手段,利用兵棋推演鍛煉指揮員戰役級作戰行動的指揮能力也成為目前我國兵棋系統應用的一大亮點.推演過程中系統實時記錄了大量真實的指揮行為實證數據,為面向兵棋推演的行為動力學研究提供了堅實的數據支撐.指揮行為動力學研究不僅有助于對指揮員的推演過程進行科學合理的分析,而且可以針對指揮員推演行為的模擬仿真和未來兵棋系統智能功能的開發打下基礎.

進入21世紀后,針對行為動力學問題的研究已經引起了有關學者的重視,并在理論層面獲得了較大的突破.奧地利經濟學家路德維希·馮·米塞斯在嘗試探索經濟學根基的過程中,最早提出了以邏輯架構為研究內容的人類行為研究方法.按照傳統近似的方法,一般將人的行為規律描述為近似泊松分布的穩態隨機過程.其主要特征體現在相繼行為之間的時間間隔方差較小,且行為的偶發狀態較少且可近似忽略.

但是,2005年,Bar˙abasi[1?2]通過統計用戶發送和回復郵件行為的時間間隔,發現時間間隔同時具有長時靜默與短時高爆發的特征,相鄰事件中的時間間隔分布呈現出近似反比冪函數的重尾特性,這種時間標度的特征是在對人類商業活動、網絡使用、管理活動、計算機指令使用等方面的時間間隔研究中得到進一步證實.大量實證統計說明人類行為可能存在滿足其他特性的動力學機制.為解釋此類特征的動力機制,Bar˙abasi[2]基于優先權決策理論構建了基于任務選擇的最高優先權優先(Highest Priority First,HPF)排隊模型.

1 HPF動力學模型描述

Bar˙abasi認為,人類行為時間上的陣發與重尾特征,是基于排隊過程的決策結果造成的.據此,Bar˙abasi[2]構建了HPF動力學模型.模型的主要思想是,人通常將需要完成的任務組合成一個動態的任務列表,然后基于個體對不同行為輕重緩急的認知差異,為它們賦予不同的優先權系數.然后,個體按照行為優先權和一定的決策協議實施行為.基于優先權優先的人類動力學模型可以描述為:

1)對行動建立一個包含L項任務的列表,每項任務具體的優先權參數xi(xi=1,2···,L)由分布函數p(x)得到;

2)隨著時間推進,每個離散時間會選擇一個任務進行處理,個體以概率p執行優先權最高的任務,并以概率1?p執行一個完全隨機的任務;

3)當一個任務完成后,會有下一個新任務對已執行任務進行替換,新任務的優先權仍由p(x)產生.

由該模型的定義[4]可知,當概率p→1時,優先權最高的任務會被執行,當概率p→0時,模型將對所有任務進行隨機選擇.在這種服務HPF規則下,被判定為優先權最高的任務,即使它最晚加入任務列表,仍然會被首選執行.這就能很好地模擬人類行為的一種規律,即人類在眾多事務需要處理時,會優先地選擇重要或者急切需要完成的事務;因此,該模型使得優先權較低的行為被新加入的優先權較高的行為插隊,低優先權的任務卻需要等待所有比其優先權高的任務都完成后才能被執行,因而低優先權的任務將被迫長時間停留在隊列中,從而產生任務執行中等待時間出現“重尾”現象.

2 模型仿真實現

根據Bar˙abasi提出的模型概念,選取事件調度法,運用MATLAB對Bar˙abasi的HPF動力學模型進行仿真模擬.事件調度法能直接對事件進行調度,通過按照特定的時序對事件進行調度,從而實現對系統動態變化的模擬.這就要求模型在執行事件調度時,要對事件進行掃描、識別、執行等程序.同時,事件列表隨著事件的選擇執行不斷進行“加入”、“刪除”等更新.

HPF動力學模型在描述上近似于帶權值的經典M/M/1模型,因此,在經典模型中加入優先權變量和模擬變量,使用MATLAB程序對模型進行程序設計,具體設計流程如圖2.模型的仿真旨在通過計算機隨機生成的模擬行為得到間隔時間的分布情況.

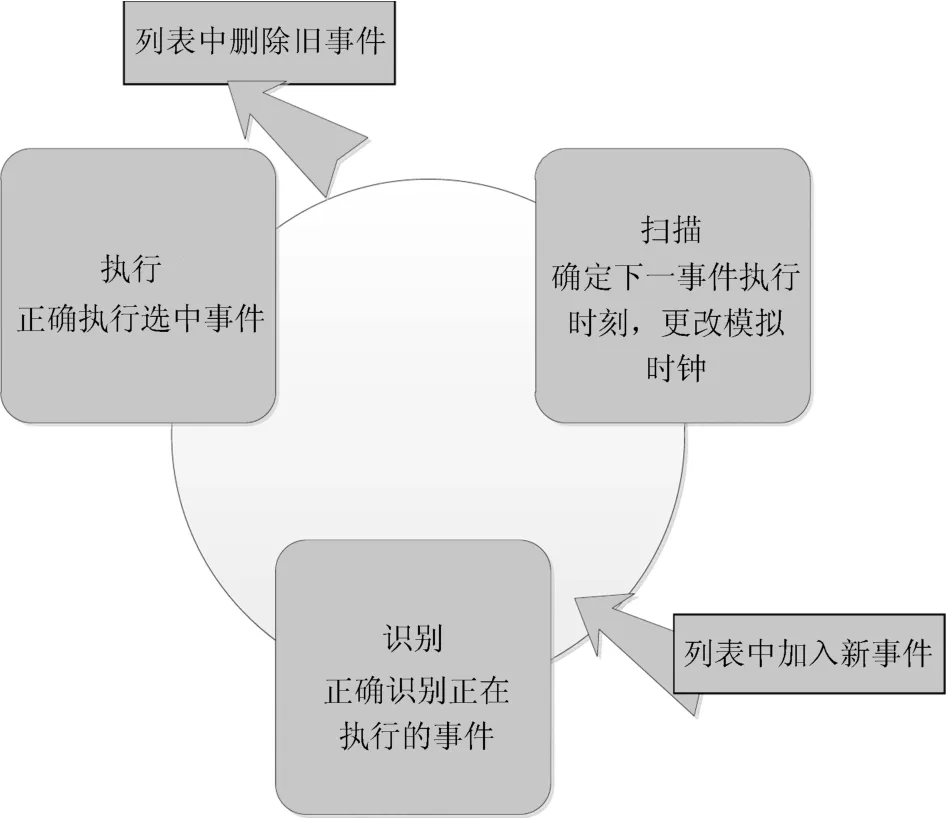
圖1 時間調度法流程示意圖

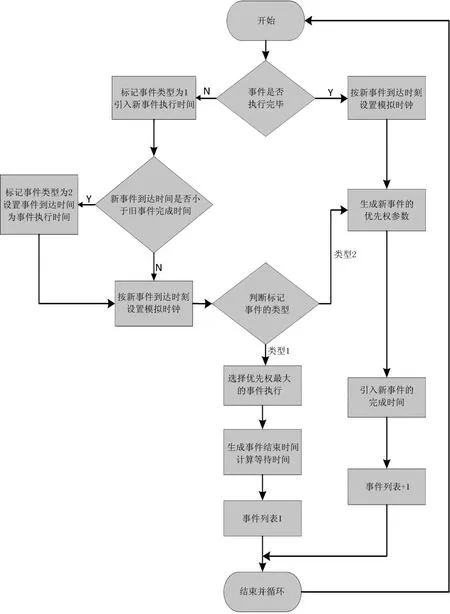
圖2 HPF模型仿真流程圖

為模擬行為選擇執行情況,模型中將所執行的任務看作相互離散的時間模擬仿真.設計模擬變量:任務到達時刻ta;任務離開時刻tb;任務列表總長L;任務優先權參數θ;模擬時間tc;結束時間td;事件類型e;時間執行時刻te,等待時間tw等.

在設置服務臺n=1、新任務到達率λ=0.8、系統服務率μ=0.5、1000次循環的情況下,仿真結果顯示模型時間間隔t與間隔時間概率P(t)在雙對數坐標系下的分布情況如圖3.由仿真結果可知,該模型能較好地反映人類行為的冪律分布及“重尾”特征.經過多次模擬,該條件下冪指數約為1.58.

3 兵棋推演中指揮行為數據時間間隔實證分析

通過對兵棋指揮行為數據進行時間維的實證分析,從中也發現了類似的特征.時間間隔分析:兵棋推演指揮行為數據集中對時間維的記錄單位為“分鐘”,由于指令下達的時間一般以秒為單位,單位分鐘的粒度較大,很難滿足指令下達的時間間隔要求,所以對時間數據進行處理.按以下規則進行時間處理:

將處理好的單位為“秒”的數據進行對于相鄰的同一指令的時間間隔分析,表1給出連續兩個相同指令時間間隔部分統計結果.

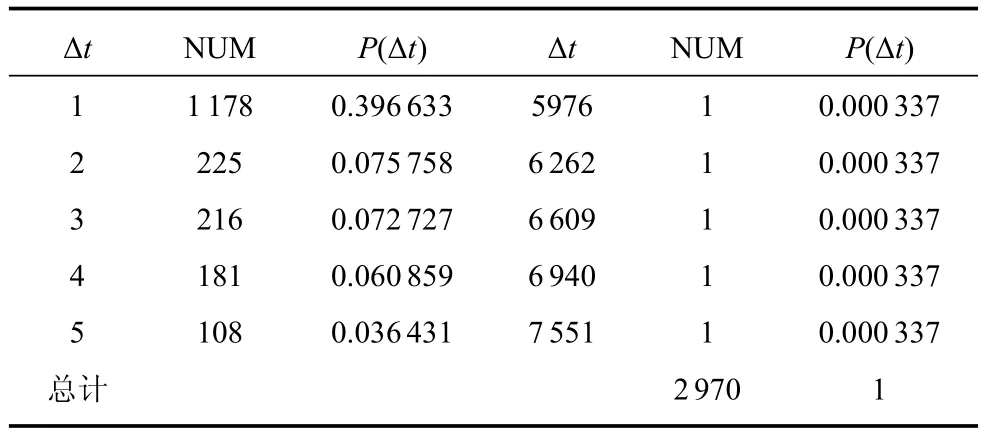
表1 一次推演過程中紅方作戰集團連續兩個相同指令下達時間間隔Δt—P(Δt)部分分布表

圖4是一次推演過程中紅方作戰集團指令下達時間間隔在雙對數坐標系下的分布圖,利用線性回歸方法對該次演習的主體數據進行擬合得到圖中直線,分析得到冪指數為1.65685,相關系數R=0.81232.而且,同一指令相鄰兩次的時間間隔最大值超過7000s,在時間間隔冪律分布圖中明顯呈現出“重尾”的特征.結果顯示,紅方作戰集團在推演過程中綜合各指令下達的時間間隔服從冪律分布.

可見,指揮員在兵棋推演過程中會在短時間內對某些指令進行快速頻繁的下達,同時在一定時間內出現某些行為的“靜默”,導致陣發和“重尾”現象同時發生.這說明指揮員在推演過程中對待各類指令的使用頻率和處理方式都是不同的,各類指令類型存在優先權差異.

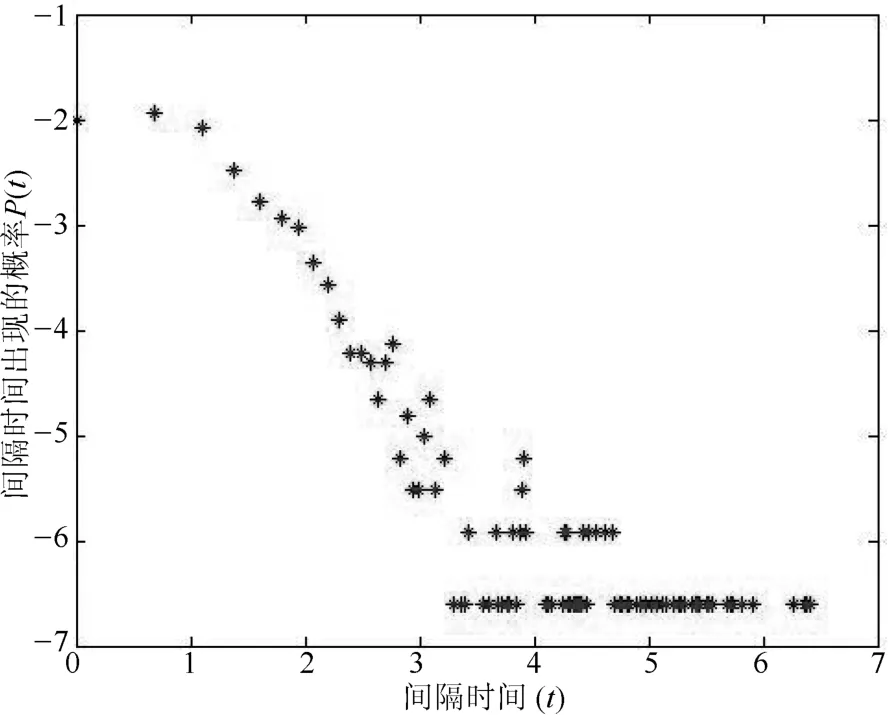
圖3 用MATLAB仿真模型的時間間隔在對數坐標系下的概率分布

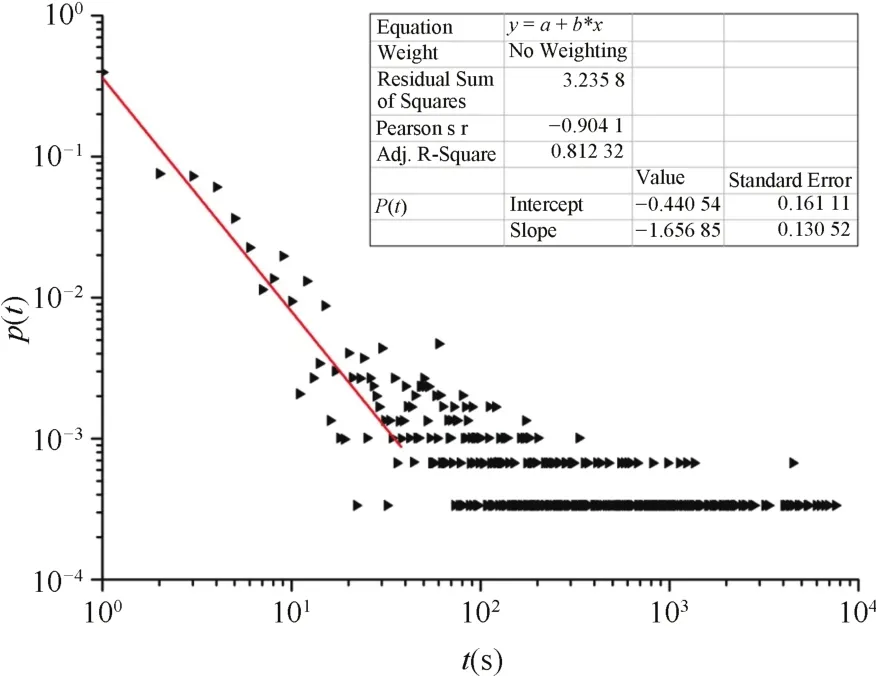
圖4 一次推演過程中紅方作戰集團連續兩個相同指令時間間隔在雙對數坐標系下分布圖

4 實證比對與模型改進

4.1 實證對比

對比圖3和圖4可以看出,模型的仿真結果與兵棋推演中實證數據的統計結果具有較大的相似度:

1)在雙對數坐標系下,模型模擬結果與實證統計結果均呈現明顯的冪率分布特征,冪指數分別為1.58、1.66;

2)兩種結果在圖中均反映出概率分布較小的大時間間隔出現,即明顯的“重尾”特征.

基于HPF動力學模型描述兵棋推演中指揮行為的時序規律在這兩方面具有較強的可用性.即可以用HPF模型對兵棋推演中指揮員下達指令的行為進行模擬和解釋.在實際推演中,指揮員根據作戰任務、作戰目標、作戰階段的不同,也可以看作將準備實施的任務按照自我認知進行不同優先級的劃分.這與Bar˙abasi提出的基于任務選擇的HPF動力學模型相契合.

4.2 動力學分析模型的改進

Bar˙abasi基于任務的行為動力模型對于兵棋推演過程具有一定的科學性,通過相鄰兩條作戰指令間隔時間的分析,得出兵棋推演中的指令下達行為近似滿足冪指數為1.65685的冪律分布.相鄰指令下達等待時間的差異間接反映了推演過程中指令的優先權的差異.基于事件優先權優先的動力模型解釋兵棋推演指揮行為的陣發、冪律分布以及“重尾特征”是可行的.但是,Bar˙abasi的動力學模型與推演行為具有一定的局限性.主要表現在兩個方面:

1)模型未考慮截止時間.由于Bar˙abasi模型優先權參數的設置是靜態的,因而無法解釋具有截止時間的行為.兵棋推演過程并不是無休止的,需要在某一規定時間內完成;

2)模型未考慮階段特征.兵棋推演數據在時間上反映出明顯的階段特征;這就需要在基于任務的模型中加入其他影響因子,本文擬將對任務的興趣引入行為動力模型的構建,即在模型中設計興趣遞減因子.當演習每一階段開始時,設置興趣因子隨時間的變化函數,從而反映推演過程的階段特征.

因此,提出一個具有服務截止時間并加入興趣遞減因子的行為動力學模型改進方案:假設事件列表的長度為L,服務時間序列服從參數θ(θ＞0)的負指數分布,且時間之間相對獨立.在時間步長在執行一個行為Fi時,首先在區間(0,1)上抽取優先權參數x1,此類事件則以概率Π(xi)=xi接受服務[4].引入時間變量t,當t=0時,事件列表為靜態L;當t＞0時,個體以概率p執行優先權最高的任務,并以概率1?p執行一個完全隨機的任務[3].假設t=0事件數為L,則列表中事件的執行概率為

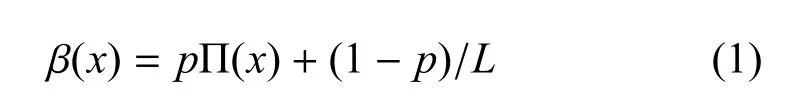
當由一個新的任務加入隊列時,模型共執行了n?1個任務的概率為

引入“興趣——時間”函數來描述興趣因子:兵棋推演的實際情況是在每個作戰階段的初始時間段參演人員對兵棋推演比較有興趣,隨著推演進程的逐步深入,參演人員對推演的興趣會有一個變高至頂點再逐漸降低的過程.當截止時間t接近T-Δt時,興趣因子會隨著時間的迫近出現一定的上升.基于這種特征,可以設置興趣因子與推演時間的函數δ(t)

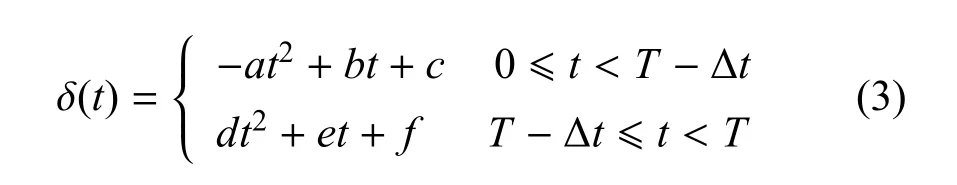
3)當t時間步長,有新的任務加入時,執行該指令的概率為:

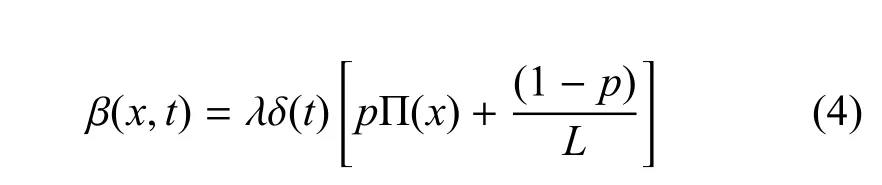
4)λ表示興趣因子的影響系數.引入截止時間和興趣因子后,模型將更加符合兵棋推演作戰指揮行為的時序特征.

5 結論

本文基于人類行為動力學相關理論,使用MATLAB對HPF模型進行了仿真實現,面向兵棋推演,時間間隔冪律分布與“重尾”特征多角度對實證數據進行了時序分析.時序分析結果顯示:一次兵棋推演過程中作戰指揮行為近似滿足冪律為1.65685的冪律分布.而后,根據兵棋推演的現實特點,引入“截止時間”和“興趣因子”對Bar˙abasi基于任務驅動的行為動力模型進行了改進.本文將根據實證分析研究結果進一步改進模型,并在未來的工作中對模型進行仿真驗證,增加模型的仿真度和可信度.