基于剛性網(wǎng)格法的潛艇水動力數(shù)值計算

劉瑞杰，劉　洋，劉一函，賈　地

（1. 中國人民解放軍92857部隊，北京 100161；2. 中國船舶重工集團公司第七一四研究所，北京 100101；3. 中國石油天然氣股份有限公司北京油氣調(diào)控中心，北京 100012）

基于剛性網(wǎng)格法的潛艇水動力數(shù)值計算

劉瑞杰1，劉洋2，劉一函3，賈地1

（1. 中國人民解放軍92857部隊，北京 100161；2. 中國船舶重工集團公司第七一四研究所，北京 100101；3. 中國石油天然氣股份有限公司北京油氣調(diào)控中心，北京 100012）

通過對潛艇六自由度空間運動方程進行分析，得到了直航阻力運動、垂直面變漂角運動、水平面變漂角運動的空間運動方程。利用 Suboff 模型，基于剛性網(wǎng)格法，通過設(shè)定計算域的運動形式，實現(xiàn)了潛艇直航阻力運動、垂直面變漂角運動、水平面變漂角運動的數(shù)值模擬，通過對計算結(jié)果進行擬合得到了線性水動力系數(shù)和非線性水動力系數(shù)，通過與相關(guān)試驗結(jié)果進行對比可知，計算誤差在 7% 左右。

ALE 方程；剛性網(wǎng)格法；變漂角運動；空間運動方程

0　引　言

潛艇作為海軍重要的作戰(zhàn)武器，對于維護國家海權(quán)、協(xié)同水面艦船作戰(zhàn)、進行戰(zhàn)略威懾具有重要意義［1］。獲取潛艇水動力系數(shù)是評價其操縱性的重要途徑。計算流體力學(xué)（CFD）作為重要的途徑，可以節(jié)省經(jīng)費、縮短研究周期，且由于獲得的水動力系數(shù)越來越準確，故越來越受到認可。

文獻［2-5］以 Suboff 模型為研究對象對潛艇定常運動進行了計算，分析了網(wǎng)格和湍流模型對計算精度的影響，并獲得了部分線型和非線性水動力系數(shù)。文獻［6］通過MRF方法將回轉(zhuǎn)運動計算轉(zhuǎn)化為定常計算，并進行了數(shù)值模擬，分析了回轉(zhuǎn)運動的原理。文獻［7-9］通過自編程序?qū)剞D(zhuǎn)運動進行了研究，分析了湍流模型、網(wǎng)格結(jié)構(gòu)、邊界層等對計算精度的影響。

以上文獻涉及到的數(shù)值計算均是基于固聯(lián)于艇體的運動坐標系，并將非定常問題通過 UDF 功能轉(zhuǎn)化為定常計算。本文以潛艇 Suboff 模型為研究對象，基于大地坐標系，借助剛性網(wǎng)格方法和Mesh Motion 功能，通過流體計算軟件 Fluent，對潛艇直航阻力運動、水平面和垂直面變漂角運動、懸臂回轉(zhuǎn)運動進行數(shù)值計算，并將計算得到的水動力系數(shù)與試驗值進行對比，驗證方法的有效性和準確性。

1　基本理論與控制方程

1.1ALE 方程

在很多運動物體模擬中，幾何體的運動可以分解為整個計算域的剛體運動和局部位置的相對運動的疊加。本文用 ALE 方程來描述這種計算域的剛性運動。其在直角坐標系下的積分形式為：

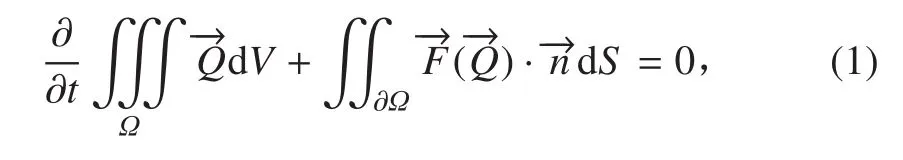
式中的解向量為：

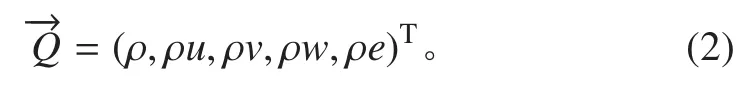
式中：Ω 為控制體，?Ω 為控制體單元的邊界；dV 為體積微元；為控制體邊界外法向單元向量；dS 為面積微元；ρ，u，v，w，e 分別為流體的密度，x，y，z軸的流體速度和單位體積流體的總內(nèi)能。

1.2剛性網(wǎng)格法

對一些特殊的運動形式可以將物體作為剛性物體處理，此時，計算域網(wǎng)格作為剛性網(wǎng)格與物體固連，所以不用在每個時間步重新生成新的網(wǎng)格，基于 ALE方程便可描述計算域的運動形式。剛性運動網(wǎng)格計算方法與固定計算域相比只是在通量計算時考慮了網(wǎng)格的運動速度。網(wǎng)格運動速度和網(wǎng)格在每個時刻點的位置由如下方法確定。

設(shè)物體的轉(zhuǎn)動軸的方程為：

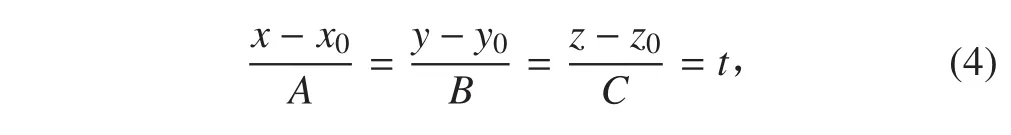
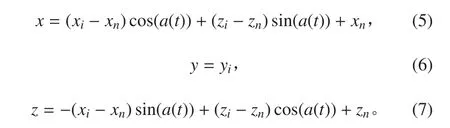
2　水動力系數(shù)數(shù)值計算實現(xiàn)

水動力系數(shù)數(shù)值計算通過以下數(shù)值試驗實現(xiàn)：直航阻力數(shù)值試驗、垂直面變漂角數(shù)值試驗、水平面變漂角數(shù)值試驗。通過 Suboff 模型，利用 Fluent 軟件實現(xiàn)各種運動。

2.1數(shù)值計算的準備

通過專業(yè)網(wǎng)格劃分軟件 ICEM CFD，采用全局映射式六面體網(wǎng)格離散方法建立網(wǎng)格。計算區(qū)域的大小是：距離潛艇前部有1 L 距離，尾部有2 L 距離，上下左右為1 L 距離。根據(jù) RNG k-ε 湍流模型對于近壁面網(wǎng)格處理方法的要求，Y+ 主要集中在（0，10），網(wǎng)格數(shù)目為360 萬。

圖1　計算域網(wǎng)格截面圖Fig. 1　Mesh graph of computational domain

2.2直航阻力數(shù)值試驗

根據(jù)縱向直航阻力試驗的特點設(shè)定計算域運動速度 u0=0.5 m/s，1 m/s，2 m/s，2.5 m/s，3.045 m/s，5.144 m/s，6.091 m/s，7.160 m/s，8.230 m/s，9.254m/s，Turbulent Intensity和Turbulent Viscosity Ratio 均設(shè)定為1%。根據(jù)直航阻力運動特點，u=u0，v=0，w=0，p=0，q=0，r=0，則六自由度空間運動方程［10］可簡化為：

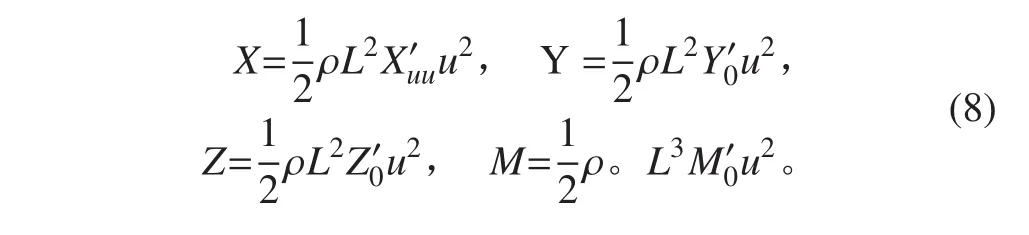
其中 u，v，w，p，q，r 分別為計算域橫向速度、縱向速度、垂向速度、橫傾角速度、縱傾角速度及偏航角速度。通過 Matlab 對計算結(jié)果進行二次樣條線擬合如圖2所示。圖3是流場的速度剖面圖。

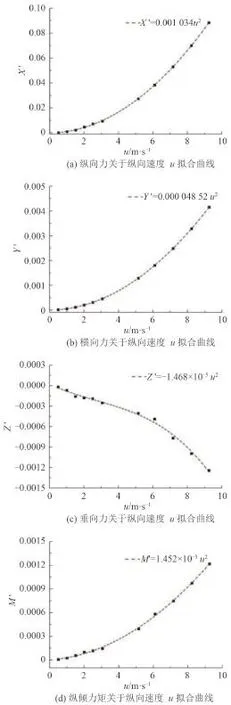
圖2　直航阻力數(shù)值試驗擬合曲線Fig. 2　Fitted curves of direct resistance numerical experiments

圖3　流場縱剖面速度分布圖Fig. 3　The longitudinal velocity distribution of flow field

2.3垂直面變漂角數(shù)值試驗

通過計算不同攻角條件下潛艇的受力和力矩，可推算相關(guān)水動力系數(shù)。假定潛艇的速度為U=3.045 m/s，攻角 α 為± 2°，± 4°，± 6°，± 8°，± 10°，± 12°，± 15°， ± 20°，± 25°，則計算域速度計算結(jié)果如圖3所示。

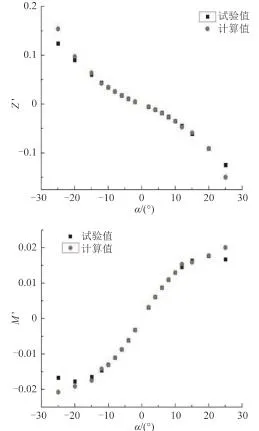
圖4　垂直面變漂角斜航試驗計算結(jié)果Fig. 4　Test results of vertical drift angle experiment

由于 Suboff 模型對稱性，故 Y0′=0，K0′=0，N0′=0。而 Mww′ 數(shù)值較小可約等于 0。垂向力Z和縱傾力矩 M 關(guān)于垂向速度 w 的函數(shù)為：

Z、M 關(guān)于不同速度 w 可得如下方程組：

解方程組并進行無因次化，可得水動力系數(shù)。

2.4水平面變漂角數(shù)值試驗

假定潛艇的速度為U=3.045 m/s，漂角 β 為± 2°，± 4°，± 6°，± 8°，± 10°，± 12°，± 14°，± 16°，由垂直面變漂角 β 試驗特點可知，u ≠ 0，v ≠ 0，w=0，p=0， q=0，r=0。計算域運動速度

由于 Suboff 模型對稱性，故 Y0′=0，N0′=0。橫向力 Y和偏航力矩 N 關(guān)于橫向速度 v 的函數(shù)為：

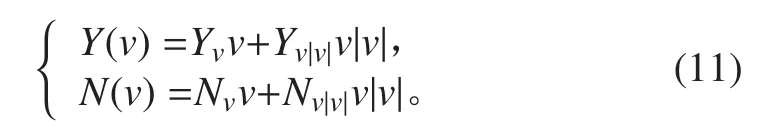
Y，N 關(guān)于不同速度 v 可得如下方程組：

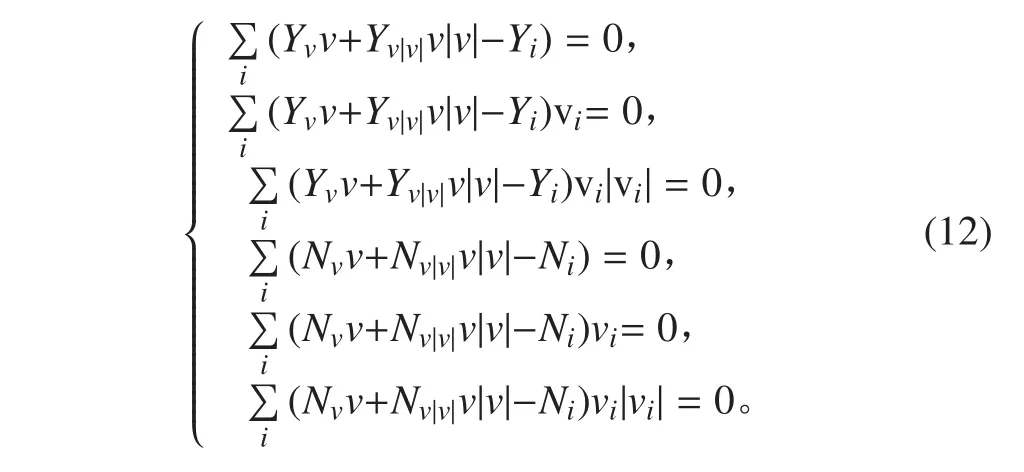
解方程組并進行無因次化，可得水動力系數(shù)。

2.5計算結(jié)果校驗

通過直航阻力數(shù)值試驗及水平面變漂角數(shù)值試驗獲得的水動力導(dǎo)數(shù)計算結(jié)果誤差為3.7%，滿足計算工程需求。通過垂直面變漂角數(shù)值試驗獲得的水動力導(dǎo)數(shù)計算結(jié)果誤差為7%，這是由于當攻角較大時，通過湍流模型計算不能準確捕捉到流動分離；而且全附體潛艇大攻角運動時，潛艇指揮臺圍殼導(dǎo)致背流區(qū)分離，而且有主附體干擾的存在，同時指揮臺圍殼對流場的干擾也會對翼產(chǎn)生影響，影響舵效及伴流場。

3　結(jié)　語

本文根據(jù)每種運動的不同，對潛艇六自由度空間運動方程進行化簡，獲得了直航阻力運動、垂直面變漂角運動、水平面變漂角運動的空間運動方程。利用Suboff 模型，基于剛性網(wǎng)格法，通過設(shè)定計算域的運動形式，實現(xiàn)了潛艇直航阻力運動、垂直面變漂角運動、水平面變漂角運動的數(shù)值模擬，通過對計算結(jié)果進行擬合得到了線性水動力系數(shù)和非線性水動力系數(shù)，通過與相關(guān)試驗結(jié)果進行對比可知，計算誤差在7% 左右。

［1］肖昌潤， 劉瑞杰， 許可， 等. 潛艇旋臂回轉(zhuǎn)試驗數(shù)值模擬［J］. 江蘇科技大學(xué)（自然科學(xué)版）， 2014， 28（4）： 313-316. XIAO Chang-run， LIU Rui-jie， XU Ke， et al. Simulation for submarine rotating-arm tests［J］. Journal of Jiangsu University of Science and Technology （Natural Science Edition）， 2014， 28（4）：313-316.

［2］劉志華， 熊鷹， 韓寶玉. 潛艇流場數(shù)值計算網(wǎng)格與湍流模型選取［J］. 華中科技大學(xué)學(xué)報（自然科學(xué)版）， 2009， 39（7）： 98-101. LIU Zhi-hua， XIONG Ying， HAN Bao-yu. Computational grid and turbulent model for calculating submarine viscous flow field［J］. Journal of Huazhong University of Science and Technology （Natural Science Edition）， 2009， 37（7）： 98-101.

［3］孫銘澤， 王永生， 張志宏， 等. 基于網(wǎng)格變形技術(shù)的全附體潛艇操縱性計算［J］. 武漢理工大學(xué)學(xué)報（交通科學(xué)與工程版），2013， 37（2）： 420-424. SUN Ming-ze， WANG Yong-sheng， ZHANG Zhi-hong， et al. Numerical simulation of submarine maneuverability based on mesh deformation technology［J］. Journal of Wuhan University of Technology （Transportation Science & Engineering）， 2013，37（2）： 420-424.

［4］柏鐵朝， 梁中剛， 周軼美， 等. 潛艇操縱性水動力數(shù)值計算中湍流模式的比較與運用［J］. 中國艦船研究， 2010， 5（2）： 22-28. BAI Tie-chao， LIANG Zhong-gang， ZHOU Yi-mei， et al. Comparison and application of turbulence modes in submarine maneuvering hydrodynamic forces computation［J］. Chinese Journal of Ship Research， 2010， 5（2）： 22-28.

［5］吳方良， 吳曉光， 許建， 等. 全附體潛艇三維粘性流場數(shù)值計算方法研究［J］. 船舶工程， 2009， 31（4）： 8-12. WU Fang-liang， WU Xiao-guang， XU Jian， et al. Study on numerical calculation method of the 3D viscous flow field over a submarine with full appendages［J］. Ship Engineering， 2009，31（4）： 8-12.

［6］劉帥， 葛彤， 趙敏. 基于源項法的潛艇旋臂試驗?zāi)M［J］. 大連海事大學(xué)學(xué)報， 2011， 37（2）： 1-4. LIU Shuai， GE Tong， ZHAO Min. Simulation for submarine rotating-arm test based on added momentum source method［J］. Journal of Dalian Maritime University， 2011， 37（2）： 1-4.

［7］GREGORY P A， JOUBERT P N， CHONG M S. Flow over a body of revolution in a steady turn［R］. Rockingham： Defence Science and Technology Organisation Victoria Platform Science Lab， 2004.

［8］TOXOPEUS S， ATSAVAPRANEE P， WOLF E， et al. Collaborative CFD exercise for a submarine in a steady turn［C］//Proceedings of the OMAE ASME 31st International Conference on Ocean Offshore and Arctic Engineering. Rio de Janeiro：ASME， 2012： 761-772.

［9］MARSHALLSAY P G， ERIKSSON A M. Use of computational fluid dynamics as a tool to assess the hydrodynamic performance of a submarine［C］//Australasian Fluid Mechanics Conference. Launceston， 2012.

［10］施生達. 潛艇操縱性［M］. 北京： 國防工業(yè)出版社， 1995.

［11］PAN Y C， ZHANG H X， ZHOU Q D. Numerical prediction of submarine hydrodynamic coefficients using CFD simulation［J］. Journal of Hydrodynamics， Series B， 2012，24（6）： 840-847.

Research on the electromechanical actuation system for submarine outboard

LIU Rui-jie1， LIU Yang2， LIU Yi-han3， JIA Di1
（1. No. 92857 Unit of PLA， Beijing 100161， China；2. The 714 Research Institute of CSIC， Beijing 100101， China；3. Beijing Oil and Gas Control Center， Beijing 100012， China）

Through analysis of submarine six degrees of freedom space motion equation， the direct resistance movement floated， vertical motion， horizontal angle of the space motion equation of angular motion. SUBOFF model， based on the rigid grid method， through setting calculation domain form of exercise， has realized the submarine direct resistance movement， vertical plane change drift angle motion， the horizontal drift Angle motion of the numerical simulation， based on the calculation results for fitting the hydrodynamic coefficient of linear and nonlinear hydrodynamic coefficients， by comparing with relevant experiment results， the calculation error is about 7%.

ALE equation；rigid grid；drift angle motion；the space motion equation

U675.6

A

1672-7619（2016）09-0065-04

10.3404/j.issn.1672-7619.2016.09.012

2016-06-12

劉瑞杰（1987-），男，研究方向為潛艇操縱性能。