基于北斗降維雙差模型的艦艇快速定姿算法研究

周志恒，趙建軍楊利斌桑德一

（1. 海軍航空工程學院 兵器科學與技術系，山東 煙臺 264001；2. 中國人民解放軍92840部隊，山東 青島 266405）

基于北斗降維雙差模型的艦艇快速定姿算法研究

周志恒1，2，趙建軍1，楊利斌1，桑德一1

（1. 海軍航空工程學院 兵器科學與技術系，山東 煙臺 264001；2. 中國人民解放軍92840部隊，山東 青島 266405）

根據北斗 GEO 衛星的特殊星座構型，提出一種基于北斗降維雙差模型的艦艇快速定姿算法。根據北斗 GEO 衛星的特點，在初始定位誤差較小的情況下，忽略Z軸誤差帶來的影響，建立降維雙差模型。利用 B1和B2頻點形成寬巷組合，根據初始偽距值計算寬巷模糊度初始值，并解算基線向量候選值；通過模糊度函數法對候選值進行判決，得到最優基線向量，解出寬巷模糊度；最后以得到的最優基線向量為初始基線向量，利用 B1頻點觀測值形成 2個雙差觀測方程，解算 B1頻點模糊度，進行艦艇定姿。利用北斗實測數據進行仿真驗證，結果表明該方法解算 B1頻點模糊度成功率高，確定的航向角標準差為0.16°，縱搖角標準差為0.07°，是一種高效快速的艦艇定姿算法。

北斗系統；艦艇定姿；降維解算；基線向量；模糊度函數法

0　引　言

在海上動態情況下的艦艇作戰系統對準過程中，被檢設備的測量數據必須利用船姿數據經過坐標平移和旋轉后才能轉化為地理坐標系數據，從而消除或修正艦艇姿態對測量結果的影響。目前，艦艇上安裝的導航設備一般為慣性導航設備（簡稱“慣導”），由于慣導本身固有的缺點，慣導所提供的艦艇姿態信息含有系統誤差，各被檢設備依據慣導提供的艦艇姿態信息進行坐標轉換時會引入新的誤差。因此，需要尋找其他高精度的艦艇姿態測量手段。

與目前廣泛應用的慣導系統相比，由于具有價格低、初始化時間短、精度高、無累積誤差等優點，基于導航衛星的多天線艦艇姿態測量系統已成為目前研究的熱點［1］。北斗衛星導航系統（以下簡稱北斗）是我國自主建設、獨立運行，并與世界其他衛星導航系統兼容共用的全球衛星導航系統，研究基于北斗系統的高精度艦艇定姿技術具有重要意義。

1　基于導航衛星的艦艇姿態測量原理

所謂艦艇的姿態，是指艦艇甲板坐標系相對于艦艇地理坐標系（當地水平坐標系）的方位關系，由航向角 CW、縱搖角 Ψ和橫搖角 θ三個姿態角來表示［2］。基于導航衛星的艦艇姿態測量是指將 2～4個衛星信號接收天線采用天線配置技術安裝在艦艇甲板上，在天線間固定基線長度的情況下，利用各天線接收衛星信號的載波相位觀測值，求在當地水平坐標系下天線間的基線向量解，根據姿態轉換矩陣與各天線的相對位置的函數關系求解艦艇的姿態角參數。使用 3 根不共線的天線垂直配置，形成雙基線測量系統，就可以完成艦艇三維姿態的測量［3］。在一般情況下，天線 1 作為主天線位于艦艇甲板坐標系的原點，天線 2和天線 3分別位于艦艇甲板坐標系的 Y 軸和X 軸。實際上，測量艦艇的姿態需要求解天線 1和天線 2 間的航向角和縱搖角，及求解天線 1和3 之間的俯仰角作為橫搖角［4］。

艦艇姿態測量是求解短基線下接收機天線相對位置的問題，根據艦艇甲板的實際情況可知，基線長度一般在幾米到幾十米。對于這種短基線來說，雙差后電離層延遲和對流層延遲基本上被消除。因此，在艦艇姿態測量中，以基線為例，載波相位雙差觀測模型為［5］：

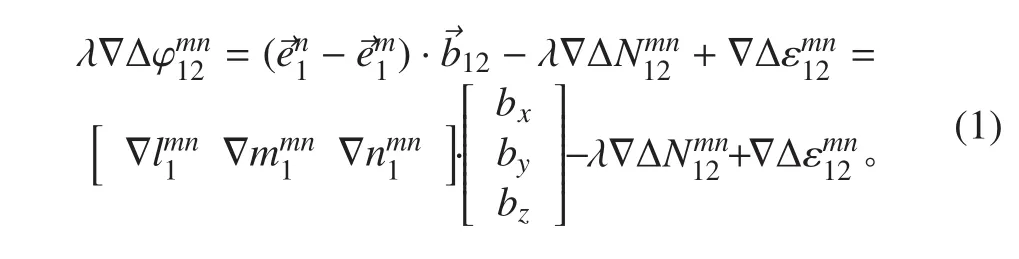
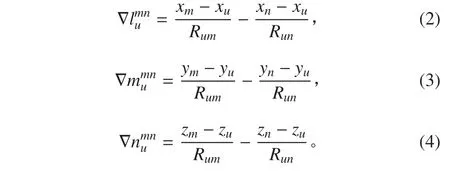
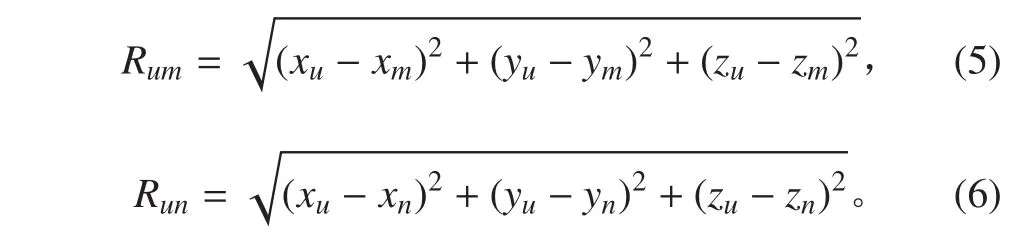
假設 t 時刻天線 1和天線 2 能同時觀測到的衛星數目為n（n ≥ 5），則可以構成（n-1）個雙差觀測方程，這里假設觀測到的衛星分別為m，n，p，q，s，且設衛星 m 為主星，忽略觀測噪聲，則將雙差方程寫成矩陣形式有：

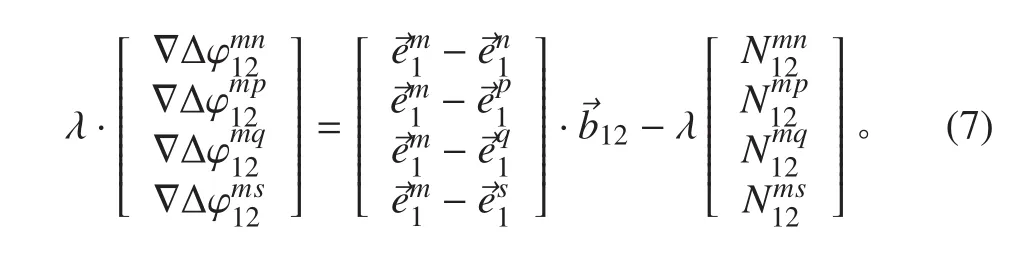
2　基于位置域的北斗快速整周模糊度確定方法

整周模糊度的正確求解，是利用載波相位測量進行衛星高精度艦艇姿態測量的關鍵問題。正確解算出整周模糊度，載波相位觀測值即可轉化為高精度的站星距離測量值，進而實現高精度的姿態測量。因此，整周模糊度的快速解算問題是進行衛星高精度定姿定位的關鍵問題，并產生了很多方法，主要可分為基于測量域、觀測域、位置域和模糊度域的整周模糊度求解方法［6］。但這些方法主要針對 GPS 提出，上述方法不一定適用于北斗系統。

其中，基于位置域的整周模糊度解算方法，主要是指模糊度函數法（Ambiguity Function Method，AFM）。模糊度函數法只利用載波相位觀測值的小數部分，因此它對周跳不敏感，并且可見星數目越多，模糊度解算的可靠性和成功率越高［7］。但其缺點是搜索空間大而導致搜索時間長和計算量大，難以實現實時動態定位。北斗系統的星座構型是區別于其他GNSS 的特點之一，通過對北斗的星座構型分析，可以發現北斗系統 GEO 衛星的Z軸雙差方向余弦系數遠遠小于 x 軸和y 軸，因此，可以將傳統的模糊度函數法的三維搜索改進為二維搜索，提高了搜索效率，減小了計算量，從而實現整周模糊度的快速固定。

2.1模糊度函數法解算原理

模糊度函數定義為［8］：

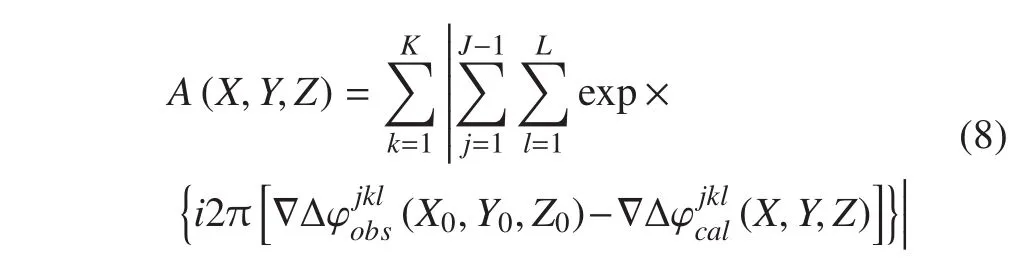
式中：K 為歷元數；J 為每歷元同步觀測到的衛星數；L 為觀測所用的頻率個數；為流動站正確位置處的雙差載波相位觀測值；為根據某一檢測點反算出來的雙差載波相位值，其計算公式為：

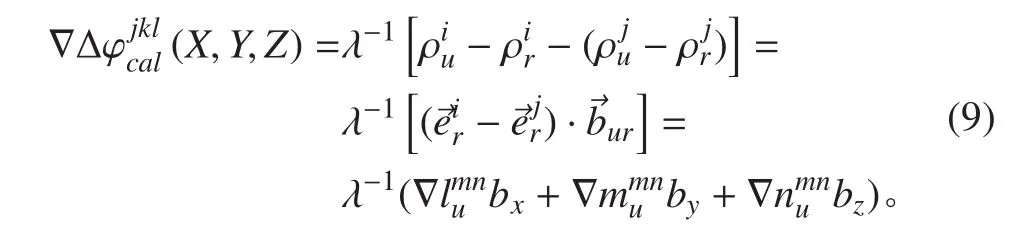
2.2北斗系統星座特性分析

目前，北斗系統星座構型為5GEO + 5IGSO + 4MEO 混合星座。通常情況下，在我國及周邊地區一般可以觀測到 8～12 顆衛星，其中包含 3～5 GEO 衛星［9］。GEO 衛星為地球靜止軌道衛星，位于赤道上空同一軌道面上。根據式（2）～式（4）計算 GEO 衛星的三維差分方向余弦系數，如圖1所示在北緯 50° 地區對 G3和G4星的三維差分方向余弦系數隨經度變化的結果。由圖1可以看出，GEO 衛星的Z軸的方向余弦系數遠遠小于 x、y 軸的方向余弦系數且接近于 0，則當 bz變化較小時，對式（1）中其余未知參數的計算結果的影響可以忽略。如果在初始定位誤差較小的情況下，在模糊度解算中忽略Z軸誤差的影響，那么原來在立體空間內的三維搜索就可以轉化為二維空間內的平面搜索，極大地減少了搜索量和計算量。

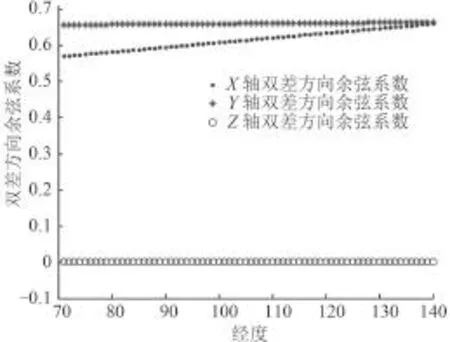
圖1　GEO 雙差方向余弦系數分析結果Fig. 1　Result of GEO double differential direction cosine coefficient analysis

2.3基于降維的位置域模糊度解算步驟

基于降維的位置域模糊度解算具體步驟如下：

1）在利用模糊度函數法進行模糊度解算時，為了提高搜索的效率，可以利用原始觀測量組成波長較長的寬巷組合。一般的北斗民用接收機可以接收到 B1和B2兩個頻率上的信號，這 2個信號可以形成寬巷組合（B1-B2），組合頻率為353.985 MHz，波長 λML為0.874 m。

2）平面搜索。采用（B1-B2）寬巷組合，由上面的分析可知，Z 軸誤差的影響可以忽略，式（9）可以寫成：

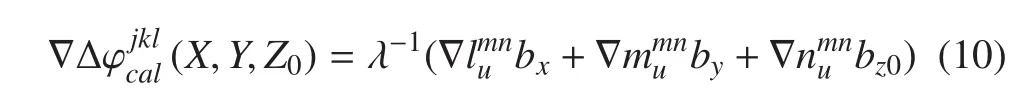
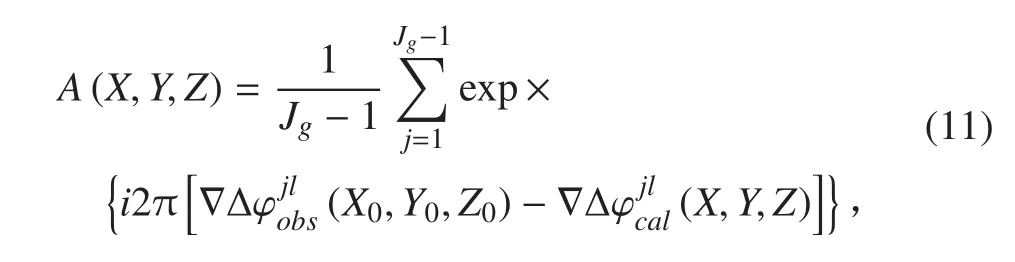
式中 Jg為可觀測的 GEO 衛星數。

改變 X和Y 坐標進行搜索，在峰值點處找到正確的 X和Y 坐標。由于只使用 GEO 衛星觀測值，在觀測衛星數較少的情況下，由于載波相位的周期性，模糊度函數表現為多峰分布的復雜非線性函數。

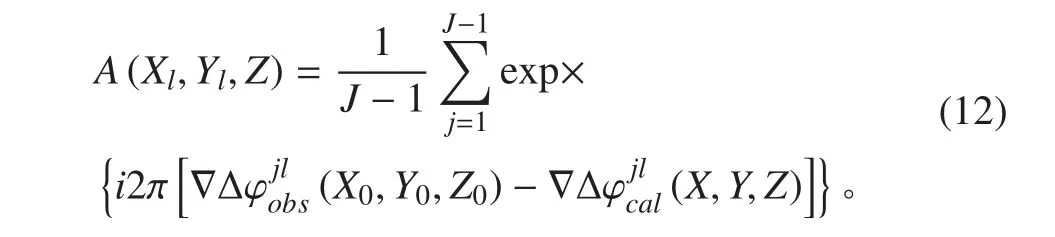
4）采用 B1頻點上的測量值在上一步確定的點附近進行精搜。得到 B1頻點上的整周模糊度，之后進行定姿解算。

3　基于北斗降維的艦艇快速定姿算法

根據北斗 GEO 衛星的特點，在初始定位誤差較小的情況下，可以忽略Z軸誤差帶來的影響。對于式（13）中的解算時可直接代入初步解算的基線向量Z軸分量來計算其余未知參量。即式可簡化為

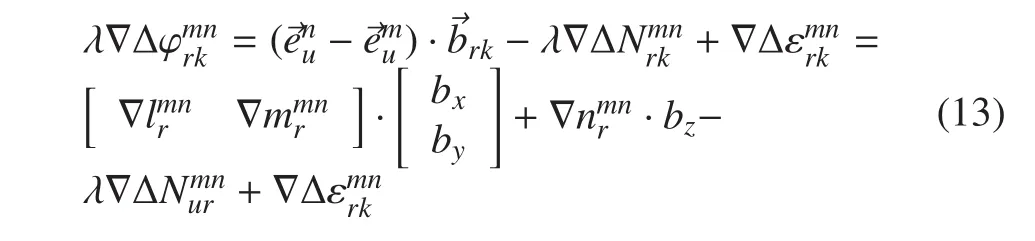
式（13）即為GEO 衛星的降維雙差模型。具體的基于北斗降維的艦艇定姿算法如下：

1）利用 B1和B2頻點上的觀測量形成寬巷組合（B1-B2），根據初始偽距值計算寬巷模糊度初始值的計算公式為

2）求解一組基線向量候選值。

選擇 3 顆二維幾何構型較好的 GEO 衛星組成 2個雙差觀測方程，根據式可得到方程組：

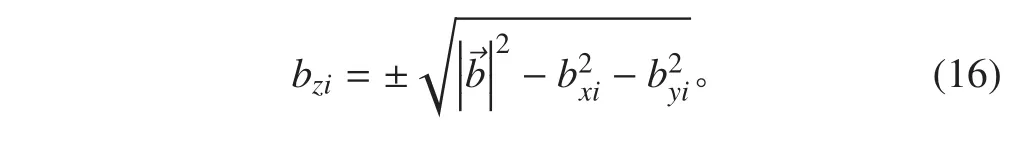
在上一步求得的 l個解中，只有一個最優解，最接近于基線向量的真實值。通過適當的判決準則可以找出這個最優解。本文的判決準則采用模糊度函數，模糊度函數定義為：

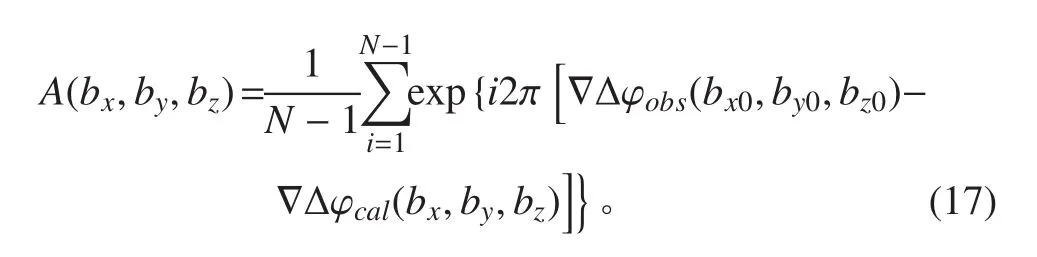
將所有可觀測衛星的寬巷雙差載波相位觀測值和l個基線解代入式，利用求解最優基線向量并計算相應的寬巷模糊度。

4）B1頻點模糊度求解。以第 3 步計算得到的最優基線向量為初始基線向量，利用 B1頻點觀測值形成 2個雙差觀測方程，按照第 2 步，得到精確的 B1頻點的模糊度。

5）利用已知整周模糊度的 B1頻點的高精度載波相位測量值進行艦艇姿態解算。

4　算法仿真

本文采用和芯星通的 UR240 雙頻接收機在短基線下采集的北斗數據進行算法驗證。天線 1位于艦艇甲板坐標系的原點，天線 2位于艦艇首尾線上，距離天線 15 m，2根天線組成單基線，用來測量艦艇的航向角和縱搖角。仿真采用的測站位置為39.54° N，115.28° S，高度為5.31 m。星歷數據為2015-8-22 09：08：00～2015-8-23 09：08：00 的北斗實際星歷，設 σφ=0.005 m，σp=0.8 m［10］，采樣間隔為30 s。

首先，利用 B1和B2頻點的組合觀測量進行寬巷結算，結果如圖3所示，其中圖3（a）為3 軸方向上的向量誤差，其中Z軸誤差在 0.2 m 以內，表明可以忽略Z軸誤差的影響；圖3（b）為三維誤差，誤差在 0.4 m以內。

圖2　改進的模糊度函數法解算流程Fig. 2　Improved ambiguity function method solving process

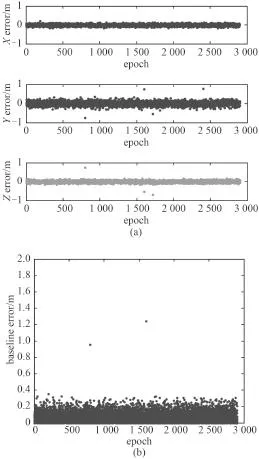
圖3　寬巷求解后的基線誤差Fig. 3　Baseline error after widelane solving

然后，利用寬巷結算的結果作為初始基線向量解進行 B1頻點模糊度求解。求解所得的解算誤差如圖4所示，圖4（a）和圖4（b）分別為3 軸方向上的誤差和三維誤差。

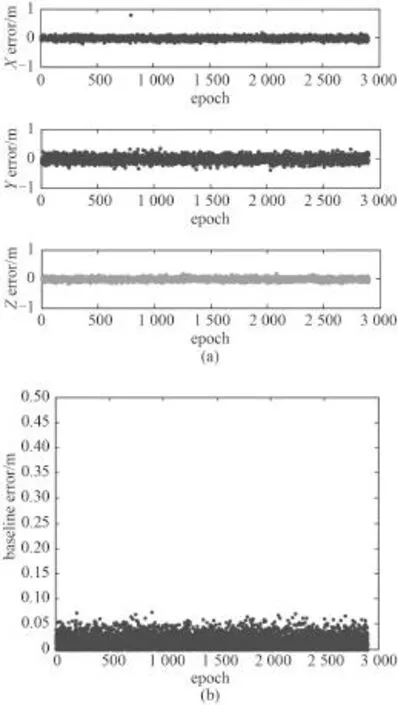
圖4　B1頻點求解后的基線誤差Fig. 4　Baseline error after B1frequency point solving

最后，利用 B1頻點解算結果進行艦艇的航向角和縱搖角解算，結果如圖5所示，航向角的標準差為0.16°，縱搖角的標準差為0.07°。

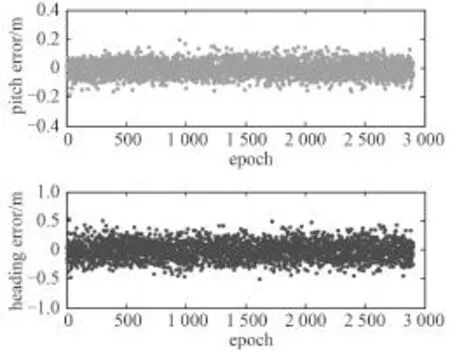
圖5　單基線定向解算誤差Fig. 5　Single baseline orientation solving error

5　結　語

本文根據北斗 GEO 衛星的特殊星座構型，提出了一種基于北斗的降維雙差模型的艦艇快速定姿算法。該方法利用降維解算方法將模糊度函數法的搜索范圍從三維轉化為二維，再利用模糊度函數法作為判決準則確定整周模糊度，并采用先求寬巷模糊度后求單個頻點模糊度的方法，進一步減少了模糊度解算的計算量。利用北斗實測數據仿真驗證，結果表明該方法解算 B1頻點模糊度成功率高，確定的航向角標準差為0.16°，縱搖角標準差為0.07°，是一種快速高效的艦艇定姿算法。

［1］楊元喜， 李金龍， 王愛兵， 等. 北斗區域衛星導航系統基本導航定位性能初步評估［J］. 中國科學： 地球科學， 2014， 44（1）：72-81. YANG Yuan-xi， LI Jin-long， WANG Ai-bing， et al. Preliminary assessment of the navigation and positioning performance of Beidou regional navigation satellite system［J］. Science China： Earth Sciences， 2014， 57（1）： 144-152.

［2］黨超. 基于北斗的航天器測姿/測速技術研究［D］. 哈爾濱： 哈爾濱工程大學， 2012. DANG Chao. Research on measuring the attitude/velocity of the spacecraft based on COMPASS［D］. Harbin： Harbin Engineering University， 2012.

［3］苑振國. GPS三維姿態測量系統的研究［D］. 哈爾濱： 哈爾濱工程大學， 2011. YUAN Zhen-guo. Research on GPS three-dimensional attitude determination system［D］. Harbin： Harbin Engineering University， 2011.

［4］鄭坤， 董緒榮， 劉亞濤， 等. GNSS載波相位多天線實時測姿系統的設計與實現［J］. 測繪科學技術學報， 2014， 31（2）：136-139. ZHENG Kun， DONG Xu-rong， LIU Ya-tao， et al. Attitude determination with a GNSS multiple-antenna system［J］. Journal of Geomatics Science and Technology， 2014， 31（2）： 136-139.

［5］PRATAP M， PER E. Global positioning system： signals， measurements， and performance［M］. Beijing： Publishing House of Electronics Industry， 2008： 188-192.

［6］陳玉林. 利用GPS載波相位信號確定載體姿態研究［D］. 南京： 南京航空航天大學， 2005： 26-27. CHEN Yu-lin. Study on attitude determination of kinematical carrier using carrier phase of GPS system［D］. Nanjing： Nanjing University of Aeronautics and Astronautics， 2005： 26-27.

［7］靳文瑞， 翟傳潤， 戰興群， 等. 基于模糊度函數法的艦船航向測量方法［J］. 中國造船， 2008， 49（S1）： 145-151. JIN Wen-rui， ZHAI Chuan-run， ZHAN Xing-qun， et al. Ship heading determination approach based on ambiguity function method［J］. Shipbuilding of China， 2008， 49（S1）： 145-151.

［8］韓紹偉. 附加約束條件的模糊度函數法及其在GPS相位差分動態定位中的應用［J］. 武漢測繪科技大學學報， 1994， 19（1）：7-14. HAN Shao-wei. Ambiguity function method with constrained conditions and its application in GPS kinematic positioning［J］. Journal of Wuhan Technical University of Surveying and Mapping， 1994， 19（1）： 7-14.

［9］趙姣姣， 曲江華， 袁洪. 一種基于位置域的北斗快速整周模糊度確定方法［J］. 測繪科學技術學報， 2014， 31（3）： 249-252. ZHAO Jiao-jiao， QU Jiang-hua， YUAN Hong. A rapid integer ambiguity resolution method based on position domain of Beidou［J］. Journal of Geomatics Science and Technology，2014， 31（3）： 249-252.

［10］MONTENBRUCK O， HAUSCHILD A， STEIGENBERGER P， et al. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system［J］. GPS Solutions， 2013， 17（2）：211-222.

Research on fast warship attitude determination algorithm based on beidou dimensionality reduction double difference model

ZHOU Zhi-heng1，2， ZHAO Jian-jun1， YANG Li-bin1， SANG De-yi1
（1. Naval Aeronautical Engineering Institute， Department of Ordnance Science and Technology， Yantai 264001， China 2. No. 92840 Unit of PLA， Qingdao 266405， China）

According to the special constellation configuration of BeiDou GEO satellite， a fast ship Attitude Algorithm which is based on Beidou dimension reduction and double difference model was presented in this paper. According to the characteristics of BeiDou GEO satellites， if the initial position error is small， the effects caused by the z-axis error could be ignored， and dimensionality reduction double difference model could be established. B1and B2frequency points were combinated to form wide lane， and calculate the initial value of wide-lane ambiguity according to the initial value of the pseudorange， and the candidate value of baseline vector can be calculated； the optimal baseline vector is obtained by judging the candidate value with ambiguity function method， and the wide lane ambiguity can be solved. Finally， the aforementioned optimal baseline vector is taken as initial baseline vector， two double difference observation equations are formed by B1frequency point observations for B1frequency ambiguity， and warship attitude is determined. The simulation example of BeiDou actual measurement shows that success rate of solving B1frequency ambiguity is high， the standard deviation of heading angle and pitching angle are 0.16° and 0.07° respectively， so the method is of high-efficiency and speediness.

Beidou system；warship attitude determination；dimensionality reduction；baseline vector；ambiguity function method（AMF）

P228

A

1672-7619（2016）09-0116-06

10.3404/j.issn.1672-7619.2016.09.024

2016-01-25；

2016-02-29

周志恒（1981-），男，博士，工程師，研究方向為作戰系統對準。