砌體結構煙囪筒體風荷載作用下的可靠度分析★
金 濤 上官子昌 * 董榅鍵
(大連海洋大學海洋與土木工程學院,遼寧 大連 116023)
?
·結構·抗震·
砌體結構煙囪筒體風荷載作用下的可靠度分析★
金濤上官子昌 *董榅鍵
(大連海洋大學海洋與土木工程學院,遼寧 大連116023)
研究了在風荷載的作用下得到砌體結構煙囪筒體受壓破壞極限狀態方程,以30 m高煙囪為例,考慮荷載效應基本組合,提出了采用蒙特卡羅法(Monte Carlo Method)并結合Matlab編程計算可靠度的方法,可供參考。
煙囪,可靠度,蒙特卡羅法
0 引言
砌體結構煙囪是目前我國排放煙氣或廢氣的主要高聳構筑物[1],由于砌體結構材料來源廣泛,造價低廉,施工簡單,目前在我國各種煙囪中砌體結構煙囪是比較常見的一種構筑物,如圖1所示。而在非地震區,風荷載為煙囪結構設計的主要水平荷載。由于煙囪特殊的體型特征,需要考慮不同情況下的可靠度指標來保證結構的工作狀態。
1 砌體結構煙囪的基本假設
在風荷載的作用下,砌體結構煙囪的應力和應變值應在變形的允許范圍內,煙囪采用燒結普通磚砌筑的筒體結構,壁厚在高度方向均勻變化,煙囪形狀及截面和壁厚剖面圖如圖2和圖3所示。
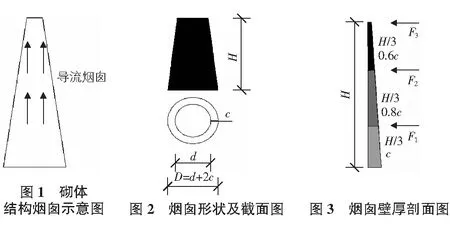
2 砌體結構煙囪在風荷載作用下的受力分析
對于大部分地區的煙囪受到的主要水平荷載為風荷載,而雨荷載和雪荷載對煙囪的作用可以忽略不計。而受到的主要豎向荷載為砌體結構煙囪的自重,它們是煙囪的主要受力荷載。
為簡化計算,采用以下基本假定:1)砌體為彈性材料;2)砌體的剛度、強度不隨時間變化;3)標準高度的年最大平均風速為伯努利實驗。
2.1水平風荷載引起砌體結構煙囪底部的彎矩M
基本風壓:水平風荷載的基準壓力,現行規范按當地空曠平坦地面上10 m高度處10 min平均的風速觀測數據,經概率統計得出50年一遇最大值來確定的風速,再考慮當地相應的空氣密度,按貝努利(Bernoulli)公式確定的風壓。
垂直于建筑物表面上的風荷載標準值,應按下列規定確定[2]:
計算主要受力結構時,應按式(1)計算:
ωk=βZμSμZω0
(1)
其中,βZ為高度Z處的風振系數;μS為風荷載體型系數;μZ為風壓高度變化系數;ω0為基本風壓,kN/m2。
煙囪在風荷載作用下的計算簡圖如圖3所示,設煙囪的底部直徑為D,煙囪的高度為H,由式(1)可得垂直于煙囪表面每段(H/3)高度上風荷載標準值的大小為(i=1,2…):
Fi=βZμSiμZiω0DiLi
(2)
其中,βZ為高度Z處的風振系數;μSi為各點處風荷載體型系數;μZi為各點處風壓高度變化系數;ω0為基本風壓,kN/m2;Li為各點處等效受荷高度;Di為煙囪各段截面直徑。
由上述式(2)得各點處等效風荷載在煙囪底部產生的總彎矩M標準值解析式如下:
(3)
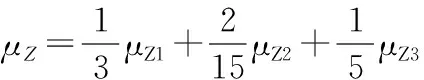
2.2豎向力作用下煙囪底部軸向壓力
設g為重力加速度,取g=10m2/s,在豎向自重力的作用下砌體結構煙囪底部的軸向壓力標準值為:
N=6.8γA0H
(4)
其中,A0為煙囪底部截面的面積,m2;H為煙囪的高度,m;γ為砌體的容重,kN/m3。
2.3煙囪底部外徑的計算公式
設d為煙囪底部的內徑,m;c為煙囪底部的壁厚,m;則煙囪底部的外徑D為:
D=d+2c
(5)
3 結構可靠度分析
結構可靠度是指在規定的時間內、規定的條件下完成預定功能的能力。計算結構可靠度的方法有很多種,本文中采用計算精度比較高的蒙特卡羅法(Monte Carlo Method)計算結構的可靠度,蒙特卡羅法根據隨機變量的分布函數選取N次隨機數輸入到分析中,計算功能函數式的值,假如失效的次數為n,因此可以用n/N來表示一個安全系數a。用Z=g(X1,X2,X3,…,Xn)來描述結構的工作狀態,則Z稱為結構的功能函數。
現以R表示結構抵抗外力的荷載,S表示作用在結構上的荷載,則結構的功能函數表達式為:Z=g(R,S)=R-S,由上式可知當R
3.2可靠度指標β的確定
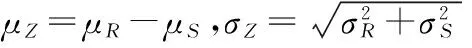
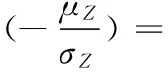
3.3砌體結構煙囪功能函數方程
砌體結構煙囪在豎向自重力和水平力風荷載共同作用下,水平截面極限承載能力應按下列公式計算[3]:
N≤φfA
(6)
(7)
β=hd/d
(8)
其中,N為在豎向力自重的作用下砌體結構煙囪底部的軸向壓力設計值,N;A為計算截面面積,m2;φ為高徑比及軸向力偏心距對承載力的影響系數;β為計算截面以上筒壁高徑比;hd為計算截面至筒壁頂端的高度,m;d為煙囪計算截面直徑,m;e0為在風荷載設計值作用下,軸向力至截面重心的偏心距,m;α為與砂漿強度等級有關的系數,當砂漿等級不小于M5時,α=0.001 5;當砂漿強度等級為M2.5時,α=0.002 0;f為砌體抗壓強度設計值,由式(9)確定:
對工件裂紋形貌檢查,選取開裂處切取一個單齒,暴露裂紋面,裂紋面宏觀檢驗,裂紋面形貌一致,呈現應力型裂紋形貌,如圖3所示。
(9)
其中,fm為砌體的強度平均值;δf為砌體強度變異系數;γf為砌體結構的材料性能分項系數,一般情況下,宜按施工質量控制等級為B級考慮,取1.60。
我國現行砌體結構規范采用的砌體強度平均值公式為:
(10)
其中,fm為砌體抗壓強度平均值,MPa;f1為塊體(磚、石、砌體)抗壓強度等級或平均值,MPa;f2為砂漿抗壓強度平均值,MPa;α為考慮砌塊高度對砌體強度的修正系數;k1為塊體類別和塊體砌筑方法的修正系數;k2為砂漿強度影響對砌體抗壓強度的修正系數。
以塊體(磚、石、砌體)抗壓強度等級或平均值f1和砂漿抗壓強度平均值f2、基本風壓ω0、砌體的容重r以及煙囪底部內徑d和壁厚c為隨機變量。結合可靠度理論,因此推導出結構功能函數表達式為:
Z=g(R,S)=g(f,ω0,r)=φfA-N
(11)
取自重和風荷載的分項系數均為1,將式(3)~式(10)代入式(11)得:
(12)
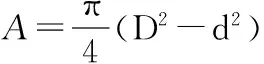
(13)
(14)
其中,H為已知常數,在本文中H=30 m。
4 砌體結構煙囪在風荷載作用下的可靠度算例
4.1隨機變量統計參數
算例:以30 m高煙囪為例,根據有關規范規定[4]:對于隨機變量基本風壓標準值ω0,新疆哈密地區30年一遇的基本風壓ω0=660 kN/m2。在設計基準期100年時,μω0=961 kN/m2,σω0=168 N/m2。查閱有關文獻可知MU30燒結普通磚和M10砂漿的抗壓強度平均值服從指數分布,分別為λ(f1)和λ(f2),通過大量實驗可知:μf1=30 MPa,σf1=1.95 MPa,μf2=10 MPa,σf2=1.16 MPa。燒結普通磚的容重γ服從N(μγ,σγ)的正態分布,μγ=1 800 kg/m3,σγ=116 kg/m3。砌體強度變異系數δf=0.10和其他各系數的取值為:砌塊高度對砌體強度的修正系數α=0.5,塊體類別和塊體砌筑方法的修正系數k1=0.78,砂漿強度影響對砌體抗壓強度的修正系數k2=1.0,風荷載體形系數μS=0.8,風振系數βZ=1.0,計算可得μZ=0.49。通過現場實地測量,得到30 m高煙囪底部的內徑d和壁厚c也近似服從N(μd,σd)和N(μc,σc)的正態分布,其中μd=3 m,μc=0.5 m,σd=σc=0.058 m。
4.2運用蒙特卡羅方法(Monte Carlo Method)
用蒙特卡羅法的關鍵是要產生隨機數,然后根據隨機變量的概率分布進行隨機抽樣。xi(i=1,2,3,…,n)進行N次隨機抽樣,得到每一個變量的樣本值xi(i=1,2,3,…,n),用所得樣本值xi(i=1,2,3,…,n)計算功能函數Z=g(R,S)的值,若總共進行了N次,如果Z<0則結構失效一次,記錄失效的次數記為nf,則結構失效的概率為:
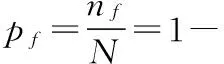
(15)
已知算例中的基本風壓標準值ω0近似服從λ(ω0)的指數分布,本文中的試驗次數為2萬次。Matlab有很大的功能,能直接產生服從各相應概率分布函數的隨機變量數組[5],如正態分布、指數分布等,可直接產生隨機變量xi(i=1,2,3,…,n)以代入功能函數中。
4.3計算結果
通過運用Matlab編程軟件并結合式(5),式(12)~式(15)計算該算例的可靠度β=3.8,可以看出,此算例砌體結構煙囪的可靠度指標滿足現行砌體結構設計規范規定的建筑結構安全等級為二級,結構構件承載力極限狀態的可靠度指標(脆性破壞)β≥3.7的要求。
5 結語
1)本文以砌體受壓破壞為極限狀態,得到煙囪在水平風荷載作用下水平截面極限承載能力可靠度的計算過程。
2)以30 m高煙囪為例,通過可靠度計算,用燒結普通磚砌筑的煙囪在風荷載作用下的可靠度指標β≥3.7,滿足現行規范中的要求。
3)用Matlab編程軟件實現蒙特卡羅方法(Monte Carlo Method)分析結構可靠度比其他分析方法更簡單適用,此方法的普遍適用性使其成為當今研究結構可靠度的很好方法,此方法將來能在結構可靠度計算中發揮巨大的作用。
[1]GB 50051—2013,煙囪設計規范[S].
[2]GB 50009—2012,建筑結構荷載規范[S].
[3]GB 50003—2011,砌體結構設計規范[S].
[4]衛軍,周錫武,張曉霞,等.超高太陽能煙囪結構可靠性計算分析[J].廣州城市職業學院學報,2007,1(11):80-86.
[5]薛定宇,陳陽泉.高等應用數學問題的MATLAB求解[M].北京:清華大學出版社,2013:47-72.
Reliability analysis of masonry structure chimney body under wind loads★
Jin TaoShangguan Zichang*Dong Wenjian
(OceanandCivilEngineeringInstitute,DalianOceanUniversity,Dalian116023,China)
Research under the wind load are deduce the concrete compression failure equation of masonry structure chimney body. Finally the paper points out a method that using Matlab programs to calculate a series of structure reliability of a 30 m-example chimney according to the Monte Carlo Method the influence basic combination of action effects are indicated, for reference.
chimney body, reliability, Monte Carlo Method
1009-6825(2016)08-0035-03
2016-01-05★:藍色學科(項目編號:34/100713025)
金濤(1987- ),男,在讀碩士;董榅鍵(1992- ),男,在讀碩士
上官子昌(1959- ),男,博士,教授,國家一級結構工程師
TU362
A

