斜拉橋損傷識別響應面模型與優化算法研究

劉杰，王海龍，張志國，呂鵬

（1.石家莊鐵道大學土木工程學院，河北石家莊050043；2.西南交通大學土木工程學院，四川成都610031；3.河北建筑工程學院土木工程學院，河北張家口075000）

斜拉橋損傷識別響應面模型與優化算法研究

劉杰1，2，王海龍2，3，張志國1，呂鵬1

（1.石家莊鐵道大學土木工程學院，河北石家莊050043；2.西南交通大學土木工程學院，四川成都610031；3.河北建筑工程學院土木工程學院，河北張家口075000）

對基于模型修正方法的響應面模型用于斜拉橋損傷識別進行了研究，通過對克里格模型、徑向基函數、Chebyshev模型、四階多項式響應面模型的計算對比可知，四階多項式響應面模型用于斜拉橋損傷識別精度最高。介紹了四階多項式模型和有約束非線性多目標優化的NSGA-Ⅱ算法，并將其用于一座單塔雙跨雙索面斜拉橋的損傷識別及損傷定位。通過設定損傷工況，證明了采用四階多項式響應面模型和NSGA-Ⅱ算法具有精度高、識別準、全局求解能力優良、計算效率高的優點。

斜拉橋損傷識別；模型修正；響應面方法；優化算法

斜拉橋損傷識別是結構健康監測中的重要內容［1］。損傷識別方法按是否有反演可分為基于模型修正的損傷識別方法和基于模式識別的損傷識別方法［2］。

基于模型修正的損傷識別方法為有反演的方法，根據修正過程中應用有限元模型的方式，模型修正法又可分為直接基于有限元模型的修正和基于響應面模型的修正［3］。前者一般需要通過理論值（計算值）、實測值之間的殘差建立目標函數，每次迭代均需進行有限元計算，模型修正時間長、計算量大，且對于大跨度橋梁來說，當待修正參數多時數值計算有可能出現病態［4］，導致無法修正。基于響應面模型的修正方法是解決這個問題的有效手段之一。響應面法是通過顯式的響應面模型逼近特征量從而得到與設計參數之間復雜的隱式函數關系式，在反應結構特性的響應面內做最優化求解［5］。響應面模型中近似核函數的選取以及用于建模的樣本數量、空間分布是影響響應面擬合精度的重要因素［6］。在相同樣本數量的前提下，能獲得較高擬合精度的響應面模型具有更好的適用性和更高的運算效率［7］。

利用獲得的響應面模型進行優化，屬于有約束非線性多目標優化。若用傳統的單目標優化方法需要對每個目標賦予權重［8］，而選取大跨度斜拉橋的多個響應權重比較困難，且傳統的優化算法難以得到全局范圍內的優值組合［9］。近年來出現的多目標優化算法具有全局搜索能力強、魯棒性、通用性好等特點，適用于處理存在多個相互沖突目標、搜索空間規模較大且高度復雜的優化問題［10］。

本文采用第2代非劣排序遺傳算法——NSGA-Ⅱ算法，該算法屬于全局探索性優化算法，避免陷入局部最優問題，可借助Matlab編制算法程序。

1　響應面模型的基本理論

用于結構優化中的響應面法是通過數學模型的方法逼近一組輸入變量（獨立變量）與輸出變量（響應變量）。該方法的引入加快了優化算法的尋優速度，推動了優化算法在工程領域中的應用，收到了良好的效果。常用的響應面模型有多項式模型［3］、Chebyshev模型［11］、徑向基函數（Radial Basis Function，RBF）模型［12］、克里格模型［13-14］等。經過計算比較發現，四階多項式模型用于大跨度斜拉橋損傷分析識別精度最高，故本文主要介紹四階多項式模型。

響應實際值與近似值之間的關系表示為

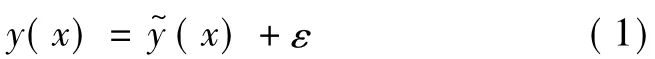
根據Weierstress多項式最佳逼近定理，任何類型的函數都可用多項式逼近，因此在實際問題中，可用多項式回歸進行分析、計算。對于大跨度斜拉橋響應與設計參數之間的高階非線性問題需要用到高階多項式模型。本文采用的四階多項式模型如下

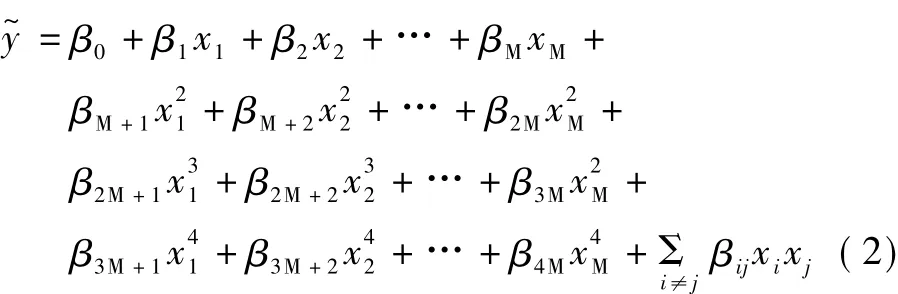
初始化所需要的最小樣本點數為（M+1）（M+ 2）/2+2M，對于分析大跨度斜拉橋，這些樣本點的數目尚不足以使模型達到較高的精度。

為提高模型的精度和質量，可通過方差分析方法（Analysis of Variance，ANOVA）以最小殘差平方和進行設計參數的顯著性檢驗，從而取舍參數，殘差平方和（Residual Sum of Squares，RSS）計算公式為

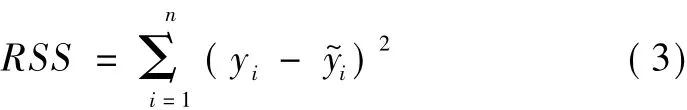
式中，n為構造響應面模型的樣本點數目。

檢驗模型精度的標準：殘差（Residual）的正態分布檢驗，殘差的均值、EISE檢驗，R2檢驗和相對均方根誤差RMS（Root Mean Square）檢驗。對于多響應問題，一般采用后2種標準，表達式分別為

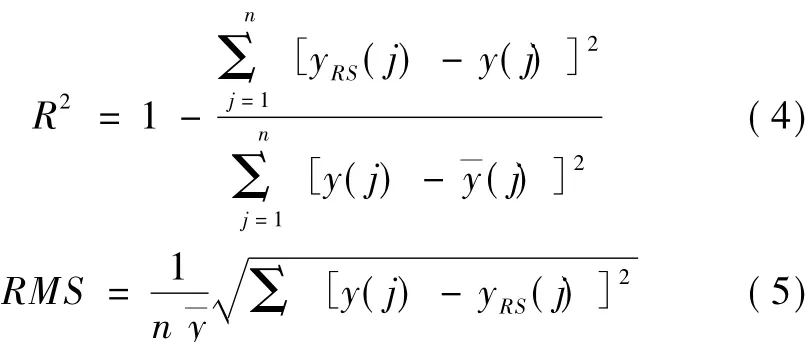
式中：yRS（j）為第j個樣本響應面模型的計算值；y（j）為對應于第j個樣本的有限元計算值；為有限元計算結果平均值。

R2值越接近1，RMS值越接近0，表明響應面模型越精確。

2　多目標優化算法

NSGA-Ⅱ是NSGA（Non-dominated Sorting Genetic Algorithm）的改良版，其優點在于探索性能良好，因為接近Pareto前沿的個體被選擇，在非支配排序中，使Pareto前進能力增強。

在具有同樣的Pareto順序的層內，由于導入了“擁擠距離”和“擁擠距離排序”的方法，可以對個體進行排序，不會削除frontier的端頭部分［15］。在目標空間中按照Pareto最優關系將群體中個體按其目標函數向量兩兩進行比較，將群體中所有個體分成多個依次控制的前沿層。利用評價Pareto優越性來評價屬于不同Pareto層個體的優劣，屬于同一個Pareto層的個體以及具有更大的擁擠距離的個體更優秀［16］。

3　基于響應面模型的損傷識別步驟

基于響應面模型修正的斜拉橋損傷識別步驟可分為4步：建立有限元模型、試驗設計（Design of Experiment，DOE）、響應面分析、優化計算。建立有限元模型是分析的基礎，基準有限元模型精確與否決定后續計算的成敗。試驗設計提供了合理而有效地獲得信息數據的方法。常用的方法有全因子設計、中心復合設計、D-最優設計、最優拉丁超立方設計（Optimal Latin Hypercube Design，Opt LHD）等，本文采用具有非常好的空間填充性和均衡性的Opt LHD方法。最后利用NSGA-Ⅱ算法進行優化計算，從而識別出損傷位置和損傷程度。

4　斜拉橋成橋試驗及損傷識別仿真

算例中，主橋為單塔雙索面預應力混凝土斜拉橋。斜拉索采用扇形布置，梁上索距6 m，橋跨為（130+ 130）m，兩跨對稱布置18對斜拉索。主梁采用預應力混凝土倒梯形的單箱4室截面，主梁中間設3道直腹板，兩側設斜腹板，端部為風嘴形狀。主梁頂面全寬37.5 m，直線上標準段頂面設雙向2%橫坡。標準斷面梁高3 m，塔梁固結區加高至3.5 m。主梁標準斷面底板寬21.9 m，底板厚28 cm，頂板厚28 cm，斜邊腹板厚28 cm，中間直腹板厚40 cm。箱梁外側懸臂寬1.55 m，厚100 cm。順橋向根據拉索間距設置橫梁，橫梁腹板厚40 cm。

采用Ansys進行建模，主梁和橋塔采用Beam 188單元，采用CAD定義截面的方式定義截面，斜拉索采用Link10單元，主梁和橋塔橫梁預應力采用等效荷載法施加，采用文獻［17］中的方法建立基準有限元模型，然后進行動力分析，提取前5階頻率，見圖1。基準有限元模型頻率與采用脈動法測得的實橋頻率對比見表1。

由表1可知，基準有限元模型頻率與實測頻率較為吻合，最大誤差為1.4%，表明基于文獻創建的基準有限元模型是可行的，其后續動力分析及損傷識別是有效的。

將塔梁聯接部位梁段、跨中、1/4跨梁段等易損部位的單元彈性模量降低程度作為設計參數，如表2所示。目標函數采用前5階頻率，設定3種多目標損傷工況，如表3所示。

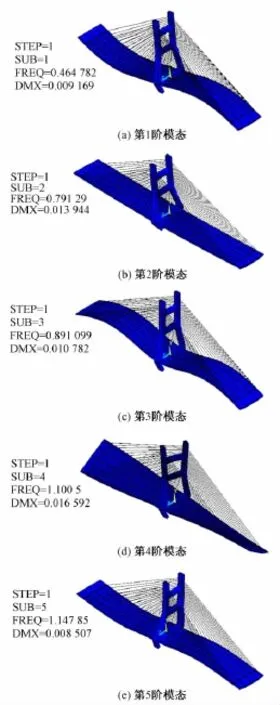
圖1　基準有限元模型的模態

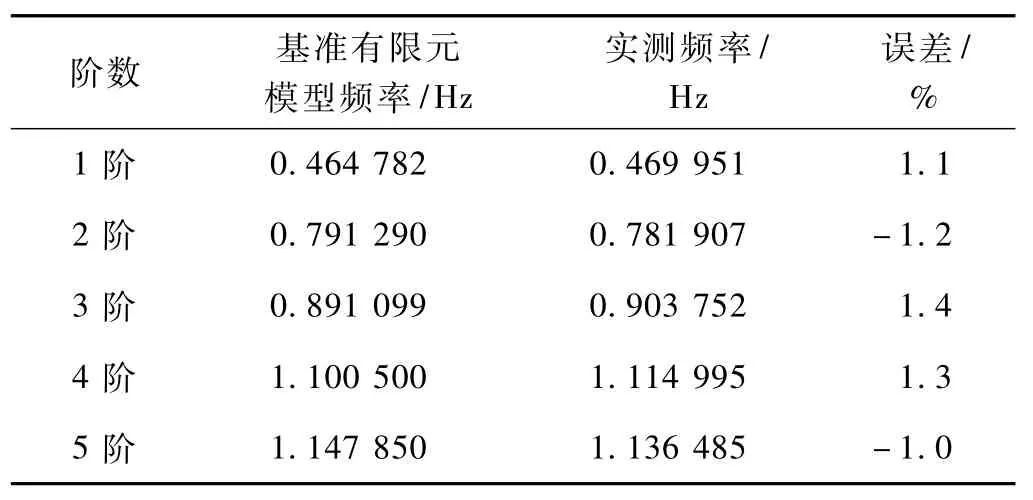
表1　基準有限元模型頻率與實測頻率對比

試驗設計采用最優拉丁超立方設計改進了隨機拉丁超立方設計的均勻性，使因子和響應的擬合更加精確真實。最優拉丁超立方設計使所有的試驗點盡量均勻地分布在設計空間，具有非常好的空間填充性和均衡性。

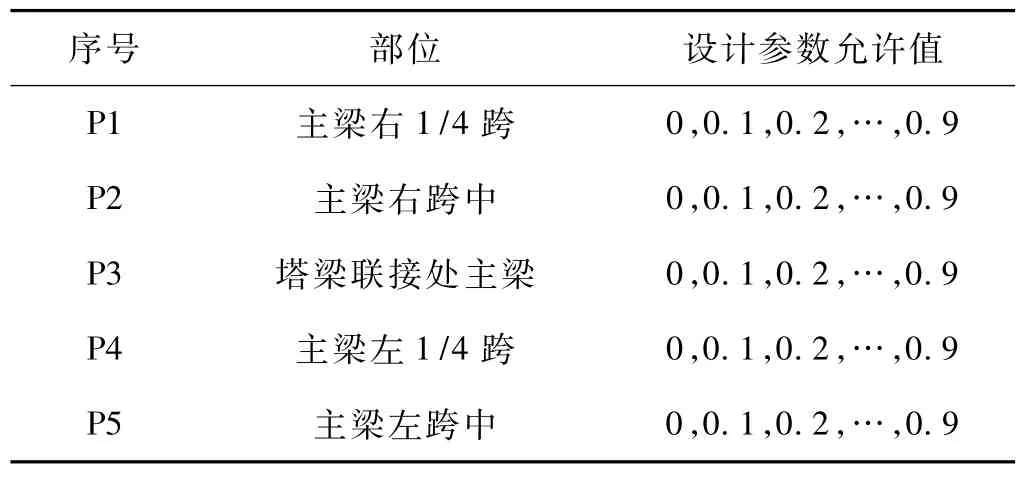
表2　設計參數允許值

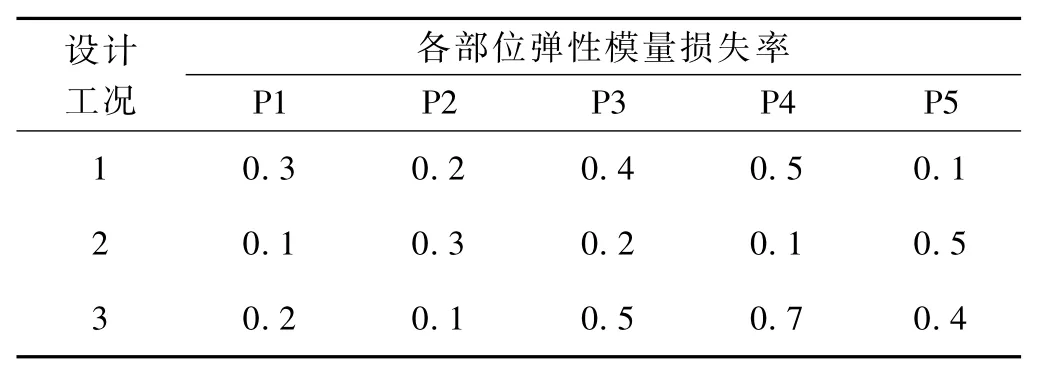
表3　損傷工況

在最優拉丁超立方設計的基礎上，分別采用克里格模型、正交多項式模型、多項式模型和徑向基函數模型進行分析。采用RMS檢驗模型精度，便于各模型的精度在同一數量級上進行比較［11］，響應面設計方法預測精度如圖2所示。

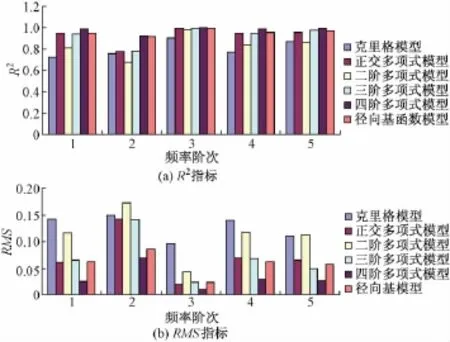
圖2　響應面設計方法預測精度

由圖2可知，克里格模型和正交多項式模型以及多項式二階、三階模型的各階或部分階RMS指標較大，且部分階R2指標較小，模型精度較低。而四階多項式模型和徑向基模型的R2指標均接近1且RMS指標較小，可知這2種模型精度較高，但二者相比前者精度更高，即四階多項式模型具有更高的精度。

采用四階多項式模型進行損傷識別計算，獲得了部分響應面，如圖3所示。

由圖3可知，各階頻率的響應面連續、光滑且有較大梯度，有利于模型修正中優化問題的求解；響應面圖形體現了待修正參數和各階頻率之間的關系。

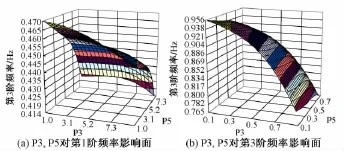
圖3　四階多項式模型響應面

利用NSGA-Ⅱ算法根據四階多項式響應面模型進行優化計算，優化結果與其種群數量、遺傳代數等因素密切相關。本文經過試算，取種群數量為100，遺傳代數為200，最優前端比為0.3，Pareto最優解分布如圖4所示。

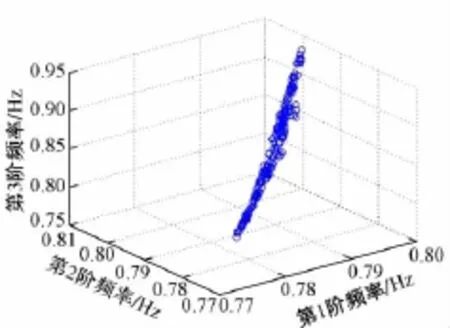
圖4　Pareto最優解分布

由圖4可知，NSGA-Ⅱ算法進化過程中，種群的Pareto前沿不斷向最優Pareto前沿演進；第1前端的Pareto最優解分布較均勻。

損傷識別計算結果與仿真結果對比如表4所示。

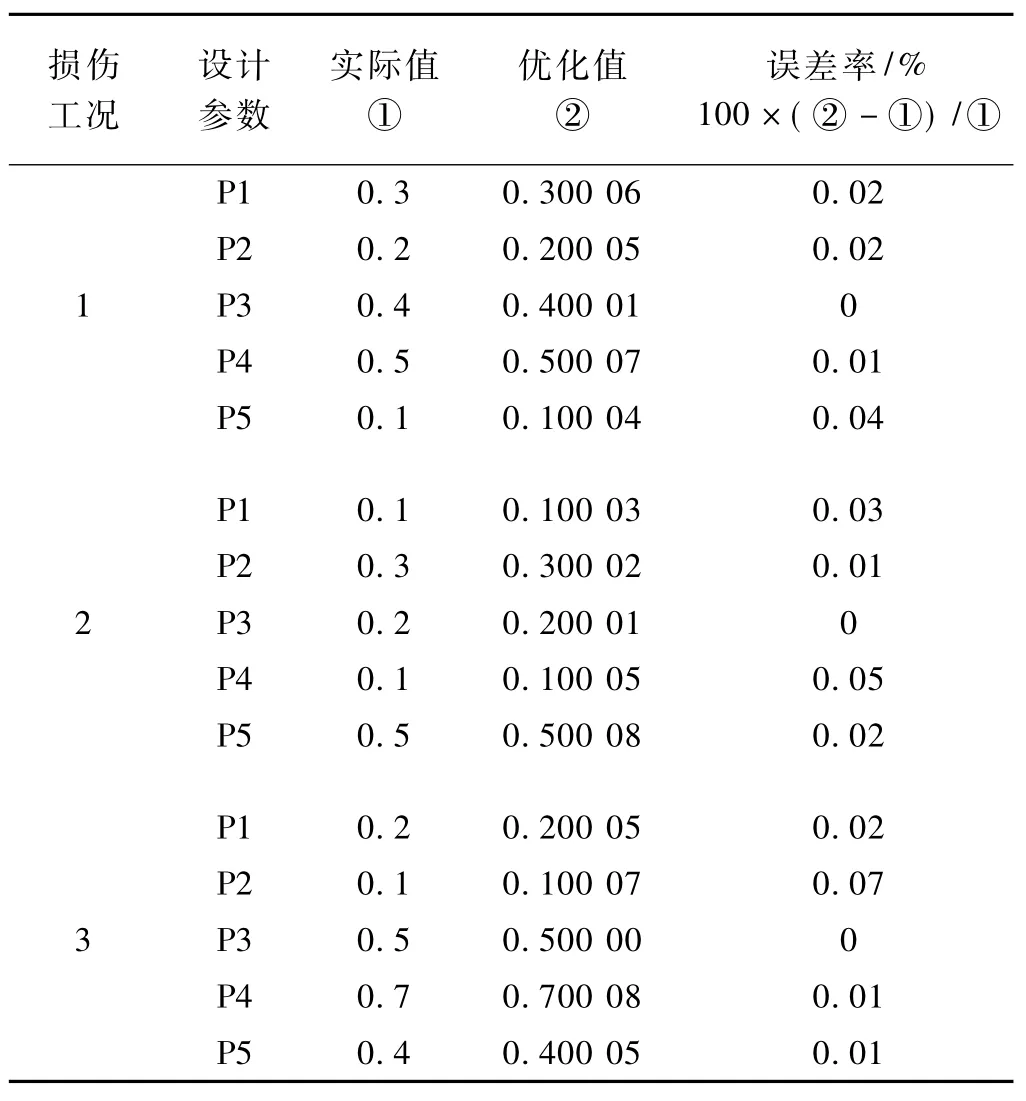
表4　損傷識別優化結果與仿真結果對比

由表4可知，優化得到的損傷位置和損傷程度與實際情況非常吻合，最大誤差不超過0.07%，說明具有較高的損傷識別精度。

5　結論

本文通過編制4種響應面模型及優化算法，對基于模型修正的斜拉橋損傷識別問題進行了研究，獲得如下結論：

1）對于大跨度斜拉橋，4種響應面模型中，四階多項式模型效率和精度最高，可用作大跨度斜拉橋損傷識別的響應面模型。

2）對于四階多項式模型獲得的斜拉橋損傷識別響應面模型，采用第2代非劣排序遺傳算法NSGA-Ⅱ算法進行優化計算，可獲得較高精度。該方法不但可以識別損傷位置，而且可以識別損傷程度。

［1］李君君，滿洪高.橋梁全自動監測系統與損傷識別技術研究［J］.鐵道建筑，2011（6）：28-33.

［2］吳向男，徐岳，梁鵬，等.橋梁結構損傷識別研究現狀與展望［J］.長安大學學報（自然科學版），2013，33（6）：49-58.

［3］宗周紅，褚福鵬，牛杰.基于響應面模型修正的橋梁結構損傷識別方法［J］.土木工程學報，2013（2）：115-122.

［4］楊小森，閆維明，陳彥江，等.基于模型修正的大跨斜拉橋損傷識別方法［J］.振動、測試與診斷，2012，32（2）：276-281.

［5］韓建平，駱勇鵬，鄭沛娟，等.基于響應面的剛構-連續組合梁橋有限元模型修正［J］.工程力學，2013，30（12）：85-90.

［6］周林仁，歐進萍.基于徑向基函數響應面方法的大跨度斜拉橋有限元模型修正［J］.中國鐵道科學，2012，33（3）：8-15.

［7］周林仁，歐進萍.大跨橋梁參數識別響應面方法中的近似函數及樣本選取［J］.計算力學學報，2012，29（3）：306-314.

［8］王開山，李傳日，龐月嬋，等.基于響應面法的印制電路板組件有限元模型修正［J］.振動與沖擊，2015，34（22）：42-46.

［9］佟晶晶，溫俊強，王丹，等.基于分時電價的電動汽車多目標優化充電策略［J］.電力系統保護與控制，2016，44（1）：17-23.

［10］程鵬，張自力.多目標進化算法測試問題的設計［J］.清華大學學報（自然科學版），2008，48（增2）：1756-1761.

［11］董春云，郭志，趙培博，等.高超聲速飛行器再入軌跡快速優化研究［J］.固體火箭技術，2015，38（6）：757-763.

［12］秦玉靈，孔憲仁，羅文波.基于徑向基函數響應面的機翼有限元模型修正［J］.北京航空航天大學學報，2011，37（11）：1465-1470.

［13］劉浩，張雷，李霄琳.基于網格變形的葉片多目標氣動優化設計［J］.華南理工大學學報（自然科學版），2015，43（9）：141-148.

［14］郁勝，周林仁，歐進萍.基于徑向基函數響應面方法的超大跨懸索橋有限元模型修正［J］.鐵道科學與工程學報，2014，11（1）：1-9.

［15］DEB K，PRATAP A，AGARWAL S，et al.A Fast and Elitist Multi-objective Genetic Algorithm：NSGA-Ⅱ［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：181-197.

［16］EPSTEIN B，JAMESON A，PEIGIN S，et al.Comparative Study of Three-dimensional Wing Drag Minimization by Different Optimization Techniques［J］.Journal of Aircraft，2009，46（2）：526-541.

［17］王海龍，劉杰，王新敏，等.建立斜拉橋基準有限元模型的新方法與實現［J］.振動、測試與診斷，2014，34（3）：458-462.

（責任審編鄭冰）

Research on Response Surface Model and Optimization Algorithm of Cable-stayed Bridge Damage Identification

LIU Jie1，2，WANG Hailong2，3，ZHANG Zhiguo1，LYU Peng1
（1.School of Civil Engineering，Shijiazhuang Tiedao University，Shijiazhuang Hebei 050043，China；2.School of Civil Engineering，Southwest Jiaotong University，Chengdu Sichuan 610031，China；3.School of Civil Engineering，Hebei University of Architecture，Zhangjiakou Hebei 075000，China）

T he response surface models for cable-stayed bridge damage identification based on model updating method were studied，including the Kriging model，radial basis function（RBF），Chebyshev model，fourth-order polynomial response surface model.According to comparison and calculation，the fourth-order polynomial response surface model has the highest accuracy.T his paper introduced the fourth-order polynomial model and nonlinear constrained multi-objective optimization of the non-dominated sorting genetic algorithmⅡ（NSGA-Ⅱ）algorithm for damage identification and location of a single tower double-span double-cable plane cable-stayed bridge.By setting the damage condition，it is proved that fourth-order polynomial response surface model and the NSGA-Ⅱalgorithm have the advantages of high precision，accurate recognition，excellent global solving ability and computational efficiency.

Cable-stayed bridge damage identification；M odel updating；Response surface method；Optimization algorithm

U448.27

A

10.3969/j.issn.1003-1995.2016.10.01

1003-1995（2016）10-0001-05

2016-03-31；

2016-08-03

國家自然科學基金（51408379）；河北省自然科學基金（E2013210104，E2013210125，E2016210087）；河北省重點學科建設基金（081406）；河北省交通廳項目（Y-2010024）；河北省科學技術廳科技計劃（09276914）

劉杰（1977—），男，講師，博士研究生。