基于改進模擬退火遺傳算法的INSAR相位解纏算法

于向明　孫學宏　劉麗萍　張　成

(寧夏大學物理電氣信息學院　寧夏 銀川 750021) 寧夏沙漠信息智能感知重點實驗室　寧夏 銀川 750021)

?

基于改進模擬退火遺傳算法的INSAR相位解纏算法

于向明孫學宏劉麗萍張成

(寧夏大學物理電氣信息學院寧夏 銀川 750021) 寧夏沙漠信息智能感知重點實驗室寧夏 銀川 750021)

為了解決經典的Goldstein枝切線法容易生成過長的枝切線和較多封閉區域的問題，提出一種基于改進模擬退火遺傳算法的INSAR(Interferometric Synthetic Aperture Radar)相位解纏算法。該算法首先對部分殘差點進行預處理，生成極性平衡的小段枝切線，然后使用改進模擬退火遺傳算法求解剩余殘差點的優化組合。經這兩步處理后，所得到的枝切線的總長度和封閉區域的數量都明顯減少。對真實INSAR數據的實驗結果表明，該算法在運行時間和解纏精度上均有一定的優越性。

干涉合成孔徑雷達相位解纏枝切線遺傳算法模擬退火

0　引　言

干涉合成孔徑雷達INSAR是一種用于獲取地面高程信息的微波遙感測量技術，它通過對同一地區的兩幅SAR圖像進行相干處理，從而獲得與高程相關的相位信息，以此反演出地面目標的高程。由于系統的原因，所提取到的相位的取值范圍在(-π,π]之間，一般稱其為纏繞相位。然而，真正與地面高程相關的是真實相位，因此，只有對纏繞相位進行相位解纏處理，恢復真實相位，才能得到地面上每個點準確的高度。在實際測量過程中，由于噪聲、欠采樣和地物不連續等因素的存在，導致干涉相位場出現不一致的現象，在相位數據中的表現均稱為殘差點，如何有效避免或降低殘差點對解纏精度造成的影響，成為了國內外學者研究的熱點。目前提出的解纏算法主要分為三類：路徑跟蹤法、最小范數法和網絡流法。其中，以路徑跟蹤法中的Goldstein枝切線法[1]最為經典和有效，作為一種局部算法，它具有流程簡單、速度快和精度高的優點。因此，在得不到實際DEM(Digital Elevation Model)數據校準的情況下，它常作為首先被嘗試的算法。但當殘差點較為密集時，Goldstein法設置的枝切線很難達到最短，而且容易圍成大量封閉區域，對后期順利解纏帶來很大影響。針對枝切線的設置問題，混合遺傳算法[2]、粒子群算法[3]、遺傳算法[4]、蟻群算法[5]等智能算法被用于求解正負殘差點的優化組合，使枝切線總長度逼近最短。但當殘差點較多時，直接使用智能優化算法會導致算法的時間和空間復雜度急劇增加，在短時間內很難得到較優的結果，影響后期的解纏精度。因此，提出了一種基于改進模擬退火遺傳算法的INSAR相位解纏算法。該算法首先對由噪聲引起的偶極子進行配對，并對靠近邊界的殘差點采取統一“接地”處理，之后對剩余的殘差點采用改進模擬退火遺傳算法求解其優化組合。對真實的INSAR數據處理結果表明，該算法較好地實現了枝切線的優化設置，提高了解纏精度。

1　殘差點與枝切線法

(1)

2　算法描述

2.1部分殘差點預處理

在干涉相位圖中，殘差點主要分為兩種形式：偶極子殘差點和單極子殘差點。其中，偶極子殘差點在干涉相位圖中以一對正負殘差點的形式出現，而單極子殘差點則以一個單一極性的殘差點的形式出現，且沒有與其配對的異性殘差點。其中，由噪聲引起的偶極子距離很近，相應的正負殘差點通常緊緊相鄰或相隔一個像素，在干涉相位圖中較好識別。因此，對此類偶極子可先進行識別并連接，同時，對靠近邊界的點可采取與邊界相連的“接地”處理，實現電量平衡。經過上述處理后，可有效減少后期需要優化的殘差點的數量，降低優化算法的壓力。算法具體步驟如下：

Step1識別干涉相位圖中的殘差點，將正負殘差點分別標記為+1、-1極性，并均標記為不平衡。

Step2找到一個不平衡的殘差點，以該殘差點為中心，放置一個3×3的搜索窗，若該點為邊界點，轉Step3，否則轉Step4。

Step3將搜索窗內所有的殘差點與中心殘差點用枝切線相連，由于進行了“接地”處理，因此，搜索窗內的所有殘差點均可標記為平衡，轉Step2。若搜索窗內無其他殘差點，則將中心殘差點標記為枝切線，并標記為平衡，轉Step2。

Step4在搜索窗內搜索異性殘差點，若找到，則將其與中心殘差點相連，并將這兩個殘差點標記為平衡，轉Step2；若未找到，則判斷當前搜索窗是否已到達邊界，若到達，則將該點與邊界相連，并標記為平衡，轉Step2，若未到達，則判斷搜索窗大小是否為5×5，若是，則放棄對該點的操作，轉Step2；若不是，則將搜索窗擴大至5×5，轉Step4。

點評：基于汽車產業在國民經濟中的重要支柱性地位，不少人建議，國家應對車輛購置稅減半征收。對于這樣的呼吁，并不難理解。作為一個重要稅種，車輛購置稅曾在2009年和2015年兩次下調，對1.6升及以下排量的乘用車減半征收購置稅，確實較好地促進了小排量乘用車的推廣和提振汽車消費。然而，這也在一定程度上提前透支了車市消費能力。

按照Step1至Step4遍歷所有殘差點后，由噪聲引起的鄰近偶極子殘差點和靠近邊界的殘差點均實現了電量平衡，剩余極性不平衡的殘差點則使用改進模擬退火遺傳算法計算其優化組合。

2.2改進模擬退火遺傳算法

遺傳算法GA(Genetic Algorithm)是一種借鑒生物界的進化規律演化而來的智能優化方法[8]，其特點是不需要求導和其他輔助信息，具有隱含的并行性，全局搜索能力較強。但在實際應用中，標準遺傳算法容易出現過早收斂和陷入局部最優解等問題，其局部搜索能力較差。模擬退火算法SA(Stimulated Annealing)是一種根據自然界中固體物質的退火降溫過程與一般組合優化問題之間的相似性所提出來的一種優化算法。該算法采用Metropolis準則來接受產生的最優問題解[9]，確保了算法在接受優解外，還能以一定的概率接受惡化解，并隨著溫度的降低使接受惡化解的概率趨向于0，從而使算法能跳離局部最優的“陷阱”，得到全局最優解。因此，模擬退火算法具有較強的“爬山”能力，即局部搜索能力較強，但該算法對整個搜索空間的情況了解不多，不能很快地使搜索過程進入最有希望的搜索區域，全局搜索能力較差。

針對這兩種算法存在的優勢和不足，本文提出一種改進模擬退火遺傳算法，該算法將模擬退火算法融入遺傳算法的交叉和變異操作中，提高遺傳算法的局部搜索能力，防止長時間陷入局部最優解。同時，使用所有殘差點及其最小相關邊編碼[10]，生成一條適應度較高的染色體，并根據該條染色體，采用最近鄰與隨機2-opt初始化方法生成整體適應度值較高的初始種群，用以加快算法的收斂速度。算法的具體步驟如下：

Step1控制參數設置。主要有最大遺傳代數、種群大小、交叉和變異概率、初始溫度、降溫速率等。

Step2編碼。采用所有殘差點及其最小相關邊編碼，該編碼方式首先將所有正負殘差點進行編號，之后逐個遍歷所有殘差點，若當前殘差點到邊界的最短距離小于其到最鄰近異性殘差點的距離的2倍，則將該殘差點與邊界相連，同時將對應的邊界點定義為一個虛擬的殘差點；若當前殘差點不滿足上述要求，則將其與最鄰近的異性殘差點相連。遍歷完所有殘差點后，將所配對的正負殘差點的排列分別建模為兩條染色體，在算法執行過程中，正殘差點對應的染色體作為參考染色體，其排列順序始終固定不變，將負殘差點對應染色體作為初始染色體。圖1左側表示對5個正殘差點和4個負殘差點的編號結果，數字的上標代表該點的極性，右側為使用所有殘差點及其最小相關邊編碼得到的結果，正殘差點對應的染色體可表示為{1B,1+,2+,3+,4B,4+,5+}，其相應的負殘差點染色體編碼為{1-,2B,2-,3B,3-,5B, 4-}，枝切線的總長度則通過計算同一基因座上所對應的正負殘差點的距離之和求出。可以看出，經過該方法編碼，所得到的染色體對應的枝切線總長度較小。

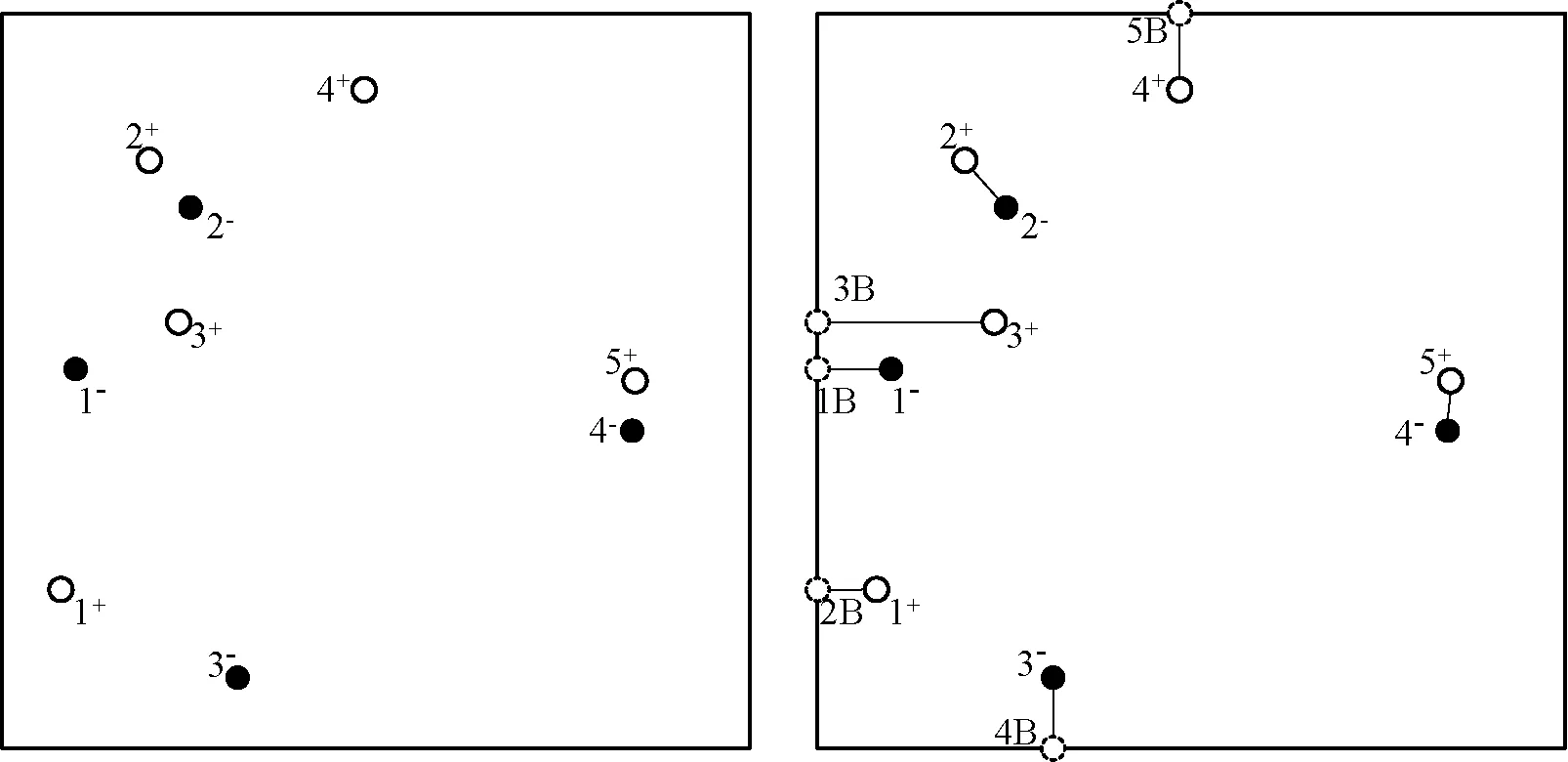
圖1　所有殘差點及其最小相關邊編碼

Step3初始化種群。經過Step2產生一條枝切線總長度較短的初始染色體后，對該條染色體采用最近鄰與隨機2-opt方法產生初始種群。即隨機選擇初始染色體中的兩個基因，交換其位置產生一條新的染色體，若新的染色體所對應的枝切線總長度小于初始染色體對應的枝切線總長度，則將新的染色體放入種群中，否則在初始染色體中重新選擇兩個基因，重復上述步驟。最終產生枝切線整體長度較短的初始種群。

Step4適應度函數。使用枝切線總長度的倒數作為適應度函數，即該條染色體所對應的枝切線長度越短，其適應度越高。

Step5選擇操作。使用隨機遍歷選擇，相比與輪盤賭，該方法可進一步提高選擇的公平性。

Step6交叉和模擬退火操作。將父代種群兩兩隨機分組，使用部分匹配交叉對每組中的染色體P1和P2執行交叉操作，得到子代染色體C1和C2，計算父代和子代對應的枝切線總長度分別為f(Pi)和f(Ci)，其中i=1,2，使用Metropolis準則接受新解，如式(2)所示。

(2)

即如果f(Ci)-f(Pi)<0，則以概率1接受新的染色體Ci，否則以概率exp[-(f(Ci)-f(Pi))/T0]接受Ci。

Step7變異和模擬退火操作。隨機選擇染色體中的兩個基因進行交換，交換前和交換后的染色體分別為S1和S2，之后采用Metropolis準則接受新解S2，方法步驟同Step6。

Step8執行降溫操作，并判斷是否達到最大遺傳代數，若是，則輸出當前適應度最高的染色體；若不是，則轉Step5繼續執行。

得到輸出的染色體后，將其與參考染色體中同一基因座的基因一一對應，即可確定殘差點組合方式，之后在干涉相位圖中用枝切線連接對應正負殘差點，最后使用洪泛法繞開枝切線進行相位解纏。

3　實驗結果與分析

實驗中使用的是伊朗BAM地區的兩幅SAR圖像，在Matlab中(計算機配置：CPU i5-4200M 內存4 GB)經配準、干涉圖生成、去平和濾波之后得到如圖2所示的700×700干涉相位圖，圖3為經四點環路積分法檢測出的殘差點，其中正殘差點(白色)2914個，負殘差點(黑色)2913個。

Goldstein法設置的枝切線如圖4所示，從圖5所示的局部放大圖可以看出在殘差點密集處，枝切線不僅較長，而且由于殘差點的重復連接，導致形成了許多封閉區域，這在后期將形成解纏“孤島”。

圖2　干涉相位圖　　　　　圖3　殘差點圖

圖4　Goldstein法設置的枝切線　　　圖5　枝切線局部放大圖

表1中給出了Goldstein法和本算法設置枝切線的量化對比。可以看出，相比于Goldstein法，本算法所設置的枝切線長度縮短36.95%， 封閉區域數量減少了98.64%，在運算時間上也得到了一定的改善。

表1　枝切線設置結果對比

本算法所設置的枝切線如圖6所示。由于本算法是將正負殘差點進行配對連接，或是將殘差點與邊界相連，因此，最終所設置的都是一些小段的枝切線，沒有圍成大面積的封閉區域。

為了進一步驗證算法在解纏精度上的有效性，將本算法和Goldstein法、質量圖引導法的解纏結果進行對比，圖7至圖9分別為這三種算法的解纏結果。

圖6　本算法設置的枝切線　　圖7　本算法的解纏結果

圖8　Goldstein法解纏結果　圖9　質量圖引導法解纏結果

同時，使用解纏誤差ε和總運算時間作為量化對比指標。其中，解纏誤差ε[11]一般采用式(3)定義。

(3)

表2　不同算法的解纏結果對比

從解纏結果中可以看出，Goldstein枝切線法形成了大量的解纏孤島，如圖8中的黑色區域所示，同時，其解纏誤差也高于其他兩種算法。質量圖引導法的解纏精度和本文算法相當，但由于該方法需要不斷對納入鄰接表中的元素進行排序，所以其運行時間很長。而本文算法將部分殘差點預處理與優化算法結合，不僅在運行時間上具有一定的優勢，同時，解纏精度也得到了一定的提高，此外，所圍成的封閉區域數量也大幅減少，這將為后期高程的反演工作帶來極大的便利。

4　結　語

針對Goldstein枝切線法存在的問題，本文提出了一種新的INSAR相位解纏算法。該算法根據殘差點的分布特點，將部分殘差點預處理與改進模擬退火遺傳算法相結合，用以實現對枝切線的優化設置。對真實INSAR數據的處理結果表明，本文提出的算法不僅在較短的時間內得到了整體長度較短的枝切線，而且使封閉區域的數量大幅降低，提高了解纏精度，相比與常用的局部解纏算法，有一定的優越性。

[1] Goldstein R M,Zebker H A,Werner C L.Satellite radar interferometry:Two-dimensional phase unwrapping[J].Radio Science,1988,23(4):713-720.

[2] Karout S A,Gdeisat M A,Burton D R,et al.Two-dimensional phase unwrapping using a hybrid genetic algorithm[J].Applied Optics,2007,46(5):730-743.

[3] 張妍,馮大政,曲小寧.基于改進粒子群算法的二維相位解纏方法[J].電波科學學報,2012,27(6):1116-1123.

[4] 曲小寧,張妍,馮大政.TSP理論在二維相位解纏的應用[J].系統工程與電子技術,2011,33(4):742-745.

[5] 魏志強,金亞秋.基于蟻群算法的InSAR相位解纏算法[J].電子與信息學報,2008,30(3):518-523.

[6] 李平湘,楊杰.雷達干涉測量原理與應用[M].北京:測繪出版社,2006:79-80.

[7] Huntley J M,Buckland J R.Characterization of sources of 2π phase discontinuity in speckle interferograms[J].Journal of the Optical Society of America A,1995,15(9):1990-1996.

[8] 于海璁,陸鋒.一種基于遺傳算法的多模式多標準路徑規劃方法[J].測繪學報,2014,43(1):89-96.

[9] 傅文淵,凌朝東.布朗運動模擬退火算法[J].計算機學報,2014,37(6):1301-1308.

[10] Gutmann B,Weber H.Phase unwrapping with the branch-cut method: clustering of discontinuity sources and reverse simulated annealing[J].Applied Optics,1999,38(26):5577-5593.

[11] Ghiglia D C,Pritt M D.Two-Dimensional Phase unwrapping:Theory,Algorithms,and Software[M].New York:Wiley,1998:293-294.

A PHASE UNWRAPPING ALGORITHM BASED ON IMPROVED STIMULATED ANNEALING GENETIC ALGORITHM FOR INTERFEROMETRIC SAR

Yu XiangmingSun XuehongLiu LipingZhang Cheng

(SchoolofPhysicsElectricalInformationEngineering,NingxiaUniversity,Yinchuan750021,Ningxia,China) (NingxiaKeyLaboratoryofIntelligentSensingforDesertInformation,Yinchuan750021,Ningxia,China)

In order to solve the problems that classical Goldstein’s branch-cuts method easily generates excessively long branch-cuts and more enclosed areas, we proposed a phase unwrapping algorithm for interferometric SAR, which is based on improved stimulated annealing genetic algorithm. First, the algorithm pre-processes part of residues to generate small piece branch-cuts with balanced polarity. Then it uses improved stimulated annealing genetic algorithm to calculate the optimised combination of remaining residues. After these two processing steps, the total length of branch-cuts derived and the number of enclosed areas decrease significantly. Results of experiment on real INSAR data proved that the proposed algorithm has certain advantage in run time and phase unwrapping precision.

Interferometric synthetic aperture radar (INSAR)Phase unwrappingBranch-cutGenetic algorithmStimulated Annealing

2015-07-16。國家自然科學基金項目(61461044)；寧夏高等學校科學技術研究項目(NGY2014007)。于向明，碩士生，主研領域：INSAR信號處理。孫學宏，副教授。劉麗萍，教授。張成，教授。

TP701

A

10.3969/j.issn.1000-386x.2016.10.051