基于M orlet小波函數(shù)的IDT建模與仿真
文理為,曾志超,牟慶豐,王代強(qiáng)
(貴州大學(xué) 大數(shù)據(jù)與信息工程學(xué)院,貴州 貴陽 550025)
基于M orlet小波函數(shù)的IDT建模與仿真
文理為,曾志超,牟慶豐,王代強(qiáng)
(貴州大學(xué) 大數(shù)據(jù)與信息工程學(xué)院,貴州 貴陽 550025)
為了得到更精確的IDT結(jié)構(gòu)模型,本文提出了基于Morlet小波函數(shù)的IDT數(shù)學(xué)模型,通過Matlab對(duì)其頻響特性進(jìn)行仿真分析,并與改進(jìn)型δ函數(shù)模型IDT結(jié)構(gòu)進(jìn)行比較。結(jié)果表明,在相同的參數(shù)情況下,校正后的Morlet小波式IDT結(jié)構(gòu)主瓣保持得很好,具有很好的通帶性和主瓣波形,相對(duì)于改進(jìn)型δ函數(shù)模型IDT結(jié)構(gòu),校正后的Morlet小波式IDT結(jié)構(gòu)旁瓣電平得到大大的抑制,聲電轉(zhuǎn)換效率更高。
Morlet小波函數(shù);IDT;Matlab;δ函數(shù)模型;頻率響應(yīng)
隨著聲表面波技術(shù)的快速發(fā)展,聲表面波器件在電子信息等領(lǐng)域的應(yīng)用越來越廣泛,與此同時(shí),為了滿足現(xiàn)代通信技術(shù)高頻化、微型化等特點(diǎn),對(duì)聲表面波器件的要求也越來越高:更高的響應(yīng)頻率、更高的帶寬、更低的插入損耗以及更小的尺寸等[1-2]。叉指換能器(IDT)作為聲表面波器件最重要的部分之一,要改善聲表面波器件的特性,提高其性能,就必須從改進(jìn)IDT結(jié)構(gòu)入手[3-4]。首先建立IDT數(shù)學(xué)模型,再對(duì)其進(jìn)行模擬仿真,并與傳統(tǒng)模型仿真結(jié)果進(jìn)行對(duì)比,改進(jìn)模型參數(shù)以滿足IDT結(jié)構(gòu)優(yōu)化的目的[5]。Morlet小波函數(shù)是一種單頻復(fù)正弦調(diào)制高斯波,具有較好的時(shí)頻特性對(duì)稱性,在頻域具有很好的線性相位特性,且其時(shí)頻域局部性非常好,是最常用的復(fù)值小波,是分析信號(hào)的強(qiáng)有力工具[6]。文中是在IDT脈沖響應(yīng)模型和改進(jìn)型δ函數(shù)模型的基礎(chǔ)上選擇Morlet小波函數(shù)對(duì)IDT進(jìn)行數(shù)學(xué)建模,再利用傳統(tǒng)數(shù)學(xué)模型對(duì)同一IDT結(jié)構(gòu)進(jìn)行仿真對(duì)比,結(jié)果表明:校正后的Morlet小波函數(shù)的IDT模型比改進(jìn)型的δ函數(shù)IDT模型更精確,達(dá)到預(yù)期結(jié)果。
1 M orlet小波函數(shù)型IDT的建立
1.1M orlet小波函數(shù)
小波函數(shù)有正交性和非正交性之分,Morlet小波函數(shù)是一種非正交波,不存在尺度函數(shù),其數(shù)學(xué)表達(dá)式為[7]:

其中,ω0為小波的中心頻率。對(duì)(1)式進(jìn)行傅里葉變換,得其頻率響應(yīng):
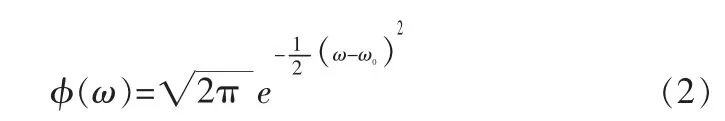
由于小波函數(shù)是處理信號(hào)的工具,SAW是變化緩慢的信號(hào),又由于小波函數(shù)的時(shí)頻窗是靈活伸縮的,因此用此特性就能靈活的設(shè)計(jì)IDT結(jié)構(gòu)[8]。
1.2改進(jìn)型IDT的δ函數(shù)模型
貴州大學(xué)王代強(qiáng)教授提出了一種改進(jìn)型δ函數(shù)模型[9],如圖1(b)所示,在IDT結(jié)構(gòu)中用邊長為aik的若干正方形來表示一根指條,并將每個(gè)正方形看作一個(gè)獨(dú)立的聲波激發(fā)源,假設(shè)有k個(gè)正方形,每個(gè)聲波激發(fā)源用基本的δ函數(shù)單元表示,再將整根叉指指條激發(fā)的SAW進(jìn)行歸一化處理。
為了表達(dá)得更明確,選取一個(gè)規(guī)則型等間距的IDT結(jié)構(gòu)進(jìn)行分析。在IDT結(jié)構(gòu)的中心取一坐標(biāo)原點(diǎn)x=0,如圖1(a)所示。同時(shí),由于IDT結(jié)構(gòu)可看作橫向?yàn)V波器,則對(duì)其場(chǎng)源分布進(jìn)行傅里葉變換可求出整個(gè)IDT結(jié)構(gòu)的頻率響應(yīng)為[10]:
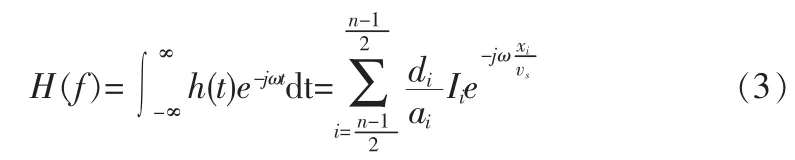
上式中,ai表示第i根叉指電極的寬度,di表示第i根叉指電極的長度,xi表示第i根叉指電極的位置,vs表示SAW的傳播速度,Ii表示第i根叉指電極的聲波幅值。
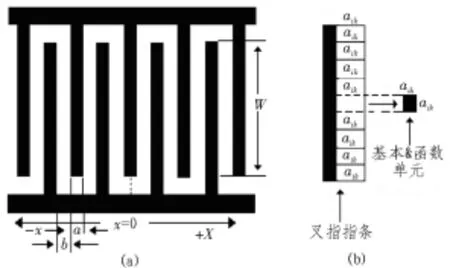
圖1 改進(jìn)型IDT結(jié)構(gòu)δ函數(shù)模型
1.3M orlet小波式IDT結(jié)構(gòu)模型
文中是在IDT的脈沖響應(yīng)模型和改進(jìn)型δ函數(shù)模型的基礎(chǔ)上提出的基于Morlet小波函數(shù)的IDT模型。構(gòu)造Morlet小波函數(shù)IDT的基本思想是IDT可看作橫向?yàn)V波器,因此,首先將想求解的的頻率響應(yīng)函數(shù)H(f)進(jìn)行變換,得到相應(yīng)的脈沖響應(yīng)函數(shù)h(t)[11]。根據(jù)抽樣定理,以1/4f0對(duì)脈沖響應(yīng)函數(shù)h(t)均勻抽樣,然后用小波函數(shù)φ(t)截?cái)啵谛〔ê瘮?shù)窗口內(nèi)得到有限長度φ(tn)·h(tn)。為了對(duì)IDT最終頻響進(jìn)行精度調(diào)整,要求計(jì)算的頻率響應(yīng)比常規(guī)方法計(jì)算的精度更高,因此采用時(shí)域上對(duì)脈沖響應(yīng)直接奇偶分解與小波窗函數(shù)截?cái)嘞嘟Y(jié)合的方法研究IDT結(jié)構(gòu)[12-13]。根據(jù)網(wǎng)絡(luò)脈沖響應(yīng)函數(shù)理論,因?yàn)镮DT的脈沖響應(yīng)與它的結(jié)構(gòu)之間有著密切的關(guān)系,很自然地想到用脈沖響應(yīng)函數(shù)去描述分析IDT結(jié)構(gòu)。在濾波器理論的基礎(chǔ)上,脈沖響應(yīng)和頻率響應(yīng)之間互為傅里葉變換對(duì),可由需要的頻響函數(shù)得到相應(yīng)的脈沖響應(yīng)函數(shù)[14]。
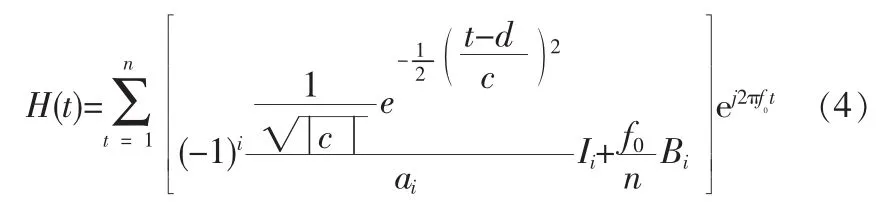
當(dāng)Morlet小波函數(shù)的伸縮因子c=1,平移因子d=0時(shí),(4)式中的脈沖響應(yīng)函數(shù)h(t)對(duì)應(yīng)的IDT結(jié)構(gòu)為Morlet母小波式IDT結(jié)構(gòu)模型。(4)式中的脈沖響應(yīng)表達(dá)式是頻率響應(yīng)函數(shù)校正后的結(jié)果,若不進(jìn)行頻率響應(yīng)函數(shù)的校正,那么h(t)結(jié)果為:
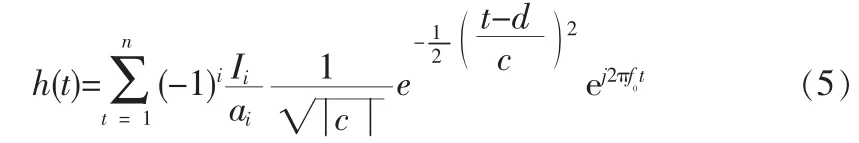
我們知道,在改進(jìn)型的δ函數(shù)模型中,為了計(jì)算更加簡單方便,選取IDT結(jié)構(gòu)的中心為一坐標(biāo)原點(diǎn)x=0。同時(shí),對(duì)于一個(gè)電極間隔b均勻的IDT結(jié)構(gòu),不管IDT結(jié)構(gòu)是否被加權(quán),它的頻率響應(yīng)都是對(duì)稱的,因此為了計(jì)算簡單方便,也取Morlet母小波式IDT中心為坐標(biāo)原點(diǎn),則整個(gè)Morlet小波式IDT的脈沖響應(yīng)為:
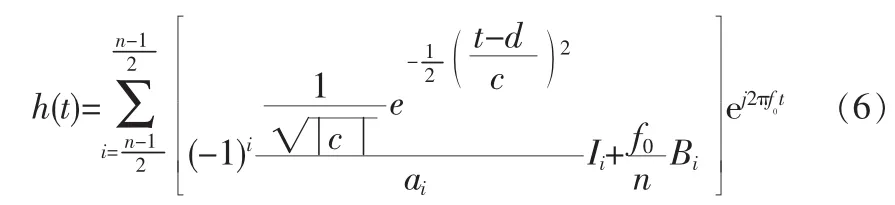
采用1/4f0對(duì)式(6)抽樣,其抽樣序列為:

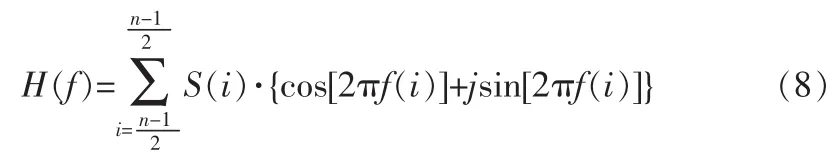
由上式可知,整個(gè)Morlet小波式IDT結(jié)構(gòu)的脈沖響應(yīng)函數(shù)是奇偶分量與校正函數(shù)之和,當(dāng)中心頻率為f0時(shí),只剩下偶分量和頻率響應(yīng)的調(diào)整函數(shù)。根據(jù)脈沖響應(yīng)函數(shù)與頻率響應(yīng)函數(shù)之間的關(guān)系,當(dāng)IDT結(jié)構(gòu)的聲孔徑長度按照Morlet母小波函數(shù)設(shè)計(jì)時(shí),小波式IDT結(jié)構(gòu)脈沖響應(yīng)函數(shù)偶分量所對(duì)應(yīng)的頻率響應(yīng)為:

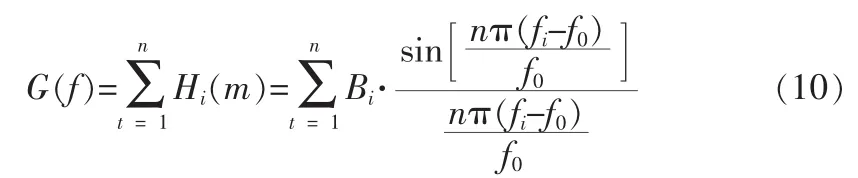
式中,Bi為第i根叉指電極的校正函數(shù)幅度,可以取正負(fù)值,fi為第i根叉指電極校正函數(shù)的調(diào)整點(diǎn)頻率。將(9)與(10)兩式相加,即:
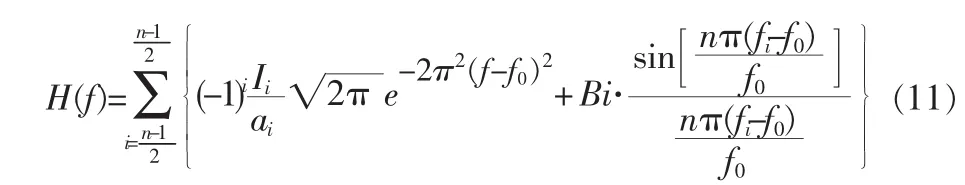
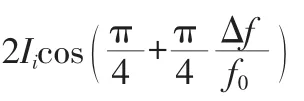
2 IDT的M orlet小波函數(shù)模型仿真
2.1IDT的M orlet小波函數(shù)模型結(jié)構(gòu)參數(shù)
為了能夠設(shè)計(jì)出IDT結(jié)構(gòu),求解出小波式IDT的叉指電極位置以及相鄰叉指間隔很關(guān)鍵,同時(shí)還需確定IDT結(jié)構(gòu)的叉指電極數(shù)和中心頻率f0。而叉指換能器的指條位置與基片材料的選取以及時(shí)間有關(guān),其關(guān)系如下:

在IDT結(jié)構(gòu)中,基片材料確定后,SAW的傳播速度vs也就確定了。因此中心頻率f0可由下式確定:

對(duì)于均勻的IDT結(jié)構(gòu),通常取ai=bi。我們知道叉指電極數(shù)n也是決定IDT結(jié)構(gòu)性能好壞的參數(shù)之一,叉指電極數(shù)不但影響著聲波的激發(fā)強(qiáng)弱,也影響著帶寬,在IDT結(jié)構(gòu)中要根據(jù)實(shí)際情況來確定其個(gè)數(shù)。
2.2仿真分析
在IDT結(jié)構(gòu)中,設(shè)每一根叉指電極有k個(gè)基本δ信號(hào)源,而且每根叉指電極產(chǎn)生的信號(hào)源強(qiáng)度與其聲孔徑Wi(t)成正比,由于SAW的激發(fā)強(qiáng)度僅與聲孔徑有關(guān),因此在本文中,將其聲孔徑按照Morlet小波函數(shù)設(shè)計(jì)時(shí),聲孔徑是可變化的,這樣就能夠得出不同的小波式IDT結(jié)構(gòu)[15]。最后結(jié)合改進(jìn)型δ函數(shù)模型以及IDT結(jié)構(gòu)的脈沖響應(yīng)模型得出其小波式IDT結(jié)構(gòu)的頻率響應(yīng)。
根據(jù)改進(jìn)型δ函數(shù)對(duì)規(guī)則IDT結(jié)構(gòu)的建模,采用Matlab數(shù)學(xué)工具,其中取叉指寬度a=7.5μm、叉指間隔b=7.5μm、叉指對(duì)數(shù)N=45,根據(jù)規(guī)則型IDT的頻率響應(yīng)表達(dá)式(3),得其結(jié)構(gòu)的頻率響應(yīng),如圖2所示。同時(shí)保持參數(shù)值不變,根據(jù)(6)式,用Matlab數(shù)學(xué)工具,仿真得到Morlet母小波式IDT的頻率響應(yīng)圖形,如圖3所示。
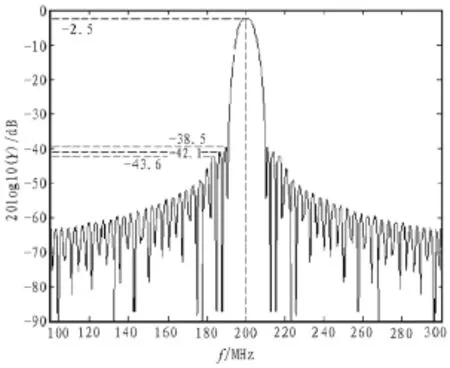
圖2 規(guī)則型IDT結(jié)構(gòu)頻響仿真圖
對(duì)比圖2和圖3,可見Morlet小波式IDT在與規(guī)則的δ函數(shù)型IDT具有同樣的叉指電極時(shí),它們的帶寬大體一樣。但是Morlet小波式IDT結(jié)構(gòu)的通帶性及主瓣波形較好,相對(duì)于規(guī)則型IDT結(jié)構(gòu),Morlet小波式IDT結(jié)構(gòu)的第一旁瓣電平抑制從38.5 dB提高到41.9 dB,第二旁瓣電平抑制從42.1 dB提高到43.7 dB,第三旁瓣電平抑制從43.6 dB提高到46.9 dB。
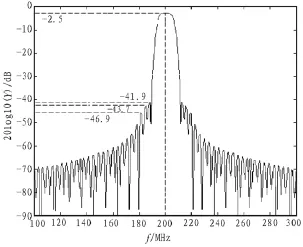
圖3 Morlet小波式IDT頻率響應(yīng)仿真圖
若對(duì) Morlet小波式 IDT結(jié)構(gòu)頻響進(jìn)行校正,根據(jù)式(11),所取參數(shù)值與上面的相同,用Matlab作為數(shù)學(xué)工具將頻率響應(yīng)仿真出來,可以得到校正后的Morlet母小波式IDT結(jié)構(gòu)的頻率響應(yīng)如圖4所示。
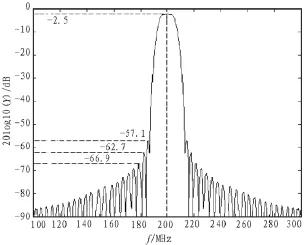
圖4 Morlet小波式IDT頻率響應(yīng)校正后的仿真圖
對(duì)比圖3、圖4,經(jīng)過校正后的Morlet小波式IDT結(jié)構(gòu)與規(guī)則型IDT結(jié)構(gòu)在叉指電極對(duì)數(shù)N相同、指寬以及間距都保持一樣時(shí),帶寬能夠保持大體相同,同時(shí),其主瓣可以保存的更好,衰減更小,有較好的通帶性,而且旁瓣電平得到了更好的抑制,第一旁瓣電平抑制從38.5 dB提高到57.1 dB,第二旁瓣電平抑制從42.1 dB提高到62.7 dB,第三旁瓣電平抑制從43.6 dB提高到66.9 dB。由于在IDT結(jié)構(gòu)中其頻率響應(yīng)的諧振峰高度與叉指電極對(duì)數(shù)N成正比,寬度與叉指電極對(duì)數(shù)N成反比,可見校正后的Morlet小波式IDT結(jié)構(gòu)具有更高的聲電轉(zhuǎn)換效率,頻率響應(yīng)特性更好。在生產(chǎn)中,可以根據(jù)實(shí)際情況,根據(jù)帶寬、中心頻率、實(shí)際濾波的需要有選擇的挑選所需要的IDT結(jié)構(gòu)。
3 結(jié) 論
文中是在IDT的脈沖響應(yīng)模型和改進(jìn)型的δ函數(shù)模型的基礎(chǔ)上提出了Morlet小波函數(shù)的IDT數(shù)學(xué)模型,采用Matlab對(duì)IDT的Morlet小波函數(shù)模型以及改進(jìn)型δ函數(shù)模型的頻響特性進(jìn)行仿真分析、比較。結(jié)果表明,改進(jìn)型δ函數(shù)型IDT結(jié)構(gòu)和校正后的Morlet小波式IDT結(jié)構(gòu)在叉指電極對(duì)數(shù)N相同、指寬以及間距都保持一樣時(shí),可以取得相同的帶寬,同時(shí),校正后的Morlet小波式IDT結(jié)構(gòu)主瓣保持得更好,衰減更小,通帶性也很好,相對(duì)于改進(jìn)型δ函數(shù)型IDT結(jié)構(gòu),校正后的Morlet小波式IDT結(jié)構(gòu)旁瓣電平得到大大的抑制,其第一旁瓣電平抑制提高了18.6 dB,第二旁瓣電平抑制提高了20.6 dB,第三旁瓣電平抑制提高了23.3 dB,這一結(jié)果說明Morlet小波式IDT結(jié)構(gòu)具有比改進(jìn)型δ函數(shù)型IDT結(jié)構(gòu)更高的精確度。
[1]徐希嬪,王代強(qiáng),劉橋.階梯型IDT結(jié)構(gòu)的仿真研究[J].現(xiàn)代電子技術(shù),2009(6):176-177.
[2]王代強(qiáng),姚祖明,陳雨青,等.圓形IDT結(jié)構(gòu)聲表面波濾波器的設(shè)計(jì)與實(shí)現(xiàn)[J].電子元件與材料,2013,32(4):50-53.
[3]王代強(qiáng),陳雨青,徐希嬪,等.變跡加權(quán)三角形IDT結(jié)構(gòu)的SAW濾波器設(shè)計(jì)與實(shí)現(xiàn)[J].西南大學(xué)學(xué)報(bào):自然科學(xué)版,2011,33(7):31-35.
[4]王代強(qiáng),陳雨青,姚祖明,等.硅基AlN橢圓形IDT-SAW濾波器的設(shè)計(jì)[J].傳感技術(shù)學(xué)報(bào),2013,26(12):1691-1694.
[5]魏培永,朱長純,劉君華.用聲表面波器件實(shí)現(xiàn)小波變換[J].壓電與聲光,2001,23(3):173-175.
[6]羅光坤.Morlet小波變換理論與應(yīng)用研究及軟件實(shí)現(xiàn)[D].南京:南京航空航天大學(xué),2007.
[7]何嶺松,李巍華.用Morlet小波進(jìn)行包絡(luò)檢波分析[J].振動(dòng)工程學(xué)報(bào),2002,15(1):119-121.
[8]LI Yuan-yuan,LU Wen-ke,GONG Lin-jia.The research of wavelet transformation technology by using surface acoustic wave devices[J].IEEE Conference Publications,2011,3:926-929.
[9]王代強(qiáng),陳雨青,徐希嬪,等.SAW器件叉指換能器δ函數(shù)模型的改進(jìn)[J].電子元件與材料,2010,29(9):62-65.
[10]Hashimoto K,Yamaguchi M.Derivation of coupling-of-modes parametersforSAWdeviceanalysisbymeansof boundaryelment method[J].IEEE Ultrason.Symp.,1991,1: 21-26.
[11]張曉慶.高頻聲表面波濾波器的納米壓印技術(shù)制備研究[D].武漢:華中科技大學(xué),2011.
[12]趙義禎.聲表面波濾波器的設(shè)計(jì)及其衍射補(bǔ)償?shù)难芯浚跠].杭州:浙江工業(yè)大學(xué),2007.
[13]董輝平.聲表面波傳感器模擬與仿真[D].太原:中北大學(xué),2008.
[14]馮亞菲.聲表面波器件的制備及其性能研究[D].哈爾濱:黑龍江大學(xué),2008.
[15]董溯前.聲表面波式小波變換器件的研究[D].上海:東華大學(xué),2008.
Modeling and simulation of IDT based on Morletwavelet
WEN Li-wei,ZENG Zhi-chao,MOU Qing-feng,WANG Dai-qiang
(College of Big Data and Information Engineering,GuiZhou University,Guiyang 550025,China)
In order to obtain a more accurate IDT(Inter Digital Transducer)structure,a new IDT mathematicalmodel is presented,based on Morlet wavelet function.Compared with the modifiedδfunction model IDT of its frequency response characteristics by Matlab.The results shows,in the case of the same parameters,the adjusted Morletwavelet IDT'smain lobe kept well,with good passband and the main lobe of the waveform.Compared with the modifiedδfunction model IDT,the sidelobe levelwasgreatly suppressed,and ithasa higheracoustic-electric conversion efficiency.
Morletwavelet function;IDT;Matlab;δfunctionmodel;frequency response
TN65
A
1674-6236(2016)19-0007-04
2016-03-14稿件編號(hào):201603158
國家自然科學(xué)基金項(xiàng)目(11564005)
文理為(1992—),男,湖南醴陵人,碩士研究生。研究方向:聲表面波器件,電路與系統(tǒng)。

