基于數值虛擬飛行技術的飛行器動態特性分析

黃宇， 閻超,*， 席柯， 王文

1.北京航空航天大學 航空科學與工程學院， 北京　100083 2.中國兵器工業導航與控制技術研究所, 北京　100089

?

基于數值虛擬飛行技術的飛行器動態特性分析

黃宇1， 閻超1,*， 席柯2， 王文1

1.北京航空航天大學 航空科學與工程學院， 北京100083 2.中國兵器工業導航與控制技術研究所, 北京100089

基于結合結構重疊網格、閉環PID控制器、舵偏控制律、剛體六自由度運動和非定常Navier-Stokes方程求解等模塊的數值虛擬飛行技術，對“起源號”返回艙、基本帶翼導彈外形的多自由度非定常運動、受控特性及控制參數的整定開展了模擬。分析了不同自由度(DOF)下飛行器的運動特性，飛行器受擾動后的穩定性及控制參數的整定。計算結果表明：利用數值虛擬飛行技術可有效地開展復雜流動下飛行物體非線性運動問題的研究，對研究飛行器在非線性流動下的動態特性、受控特性、流動機理研究以及控制律的設計檢驗具有較高的工程價值和應用前景。

計算流體力學(CFD)； 重疊網格； PID控制； 虛擬飛行； 動導數； 控制參數整定； 動態特性； 非定常流動

飛行器在大迎角、過失速等狀態下飛行時，會出現復雜的分離渦等強非線性、非定常流動，與飛行器運動耦合將會使飛行器產生一系列的非定常運動現象，如極限環搖滾、俯仰振蕩等，從而引起飛行器氣動力的突變、遲滯及非對稱特性，極易導致飛行器運動進入發散狀態，嚴重影響飛行器的安定性、穩定性及受控性。由此，現代先進空戰武器設計對飛行器的動態特性、穩定性及控制效率等的預測技術提出了要求[1]。

飛行器出現非定常、非線性流動情況下，線性化數據不能正確地刻畫飛行器非線性的氣動力和運動規律[2-3]。為了能有效地研究飛行器非定常運動中的氣動、控制等問題，國內外研究人員從20世紀80年代開始發展了一種新型的風洞試驗技術，即風洞虛擬飛行技術[4-6](Wind Tunnel Based Virtual Flight Testing)。通過將實驗縮比模型安裝有若干個自由度的支撐機構上，在風洞中開展運動模型的動力特性、控制特性的綜合實驗，在一定程度上模擬飛行器的真實飛行狀態，獲得飛行器動態品質及控制特性。但由于風洞試驗的固有缺陷，如支架/洞壁干擾、機械阻尼、相似準則等難以完全滿足等情況，導致難以準確地測量動態參數。此外，由于風洞一般只能提供直勻流，且模型支撐機構并不能在大范圍內實現真實飛行自由度，因而模擬的仿真程度也受到制約。

近年來，計算流體力學(Computational Fluid Dynamics， CFD)及大規模高性能計算技術發展迅速，CFD在基礎理論和工程實踐上都取得了令人矚目的成就，以CFD技術為基礎實現的基于方程的數值虛擬飛行技術已經成為可能[7-8]。數值虛擬飛行技術將飛行動力學方程/流體力學方程/控制律耦合實時求解，可開展全尺寸，真實運動/氣流參數的非定常模擬，避免了風洞虛擬飛行技術的固有缺點，運動仿真程度更高。此外數值虛擬飛行技術靈活性更好、耗費低、周期短，在機理研究中對流場、運動參數的獲取更為方便和豐富，在實際工程應用中可在各個階段介入研究，為設計及驗證飛行器氣動、控制等系統的特性提供有力的依據，填補風洞虛擬飛行及飛行試驗的不足[9]。

本文基于數值虛擬飛行技術，開展了返回艙、帶翼導彈外形的動態特性研究。研究結果表明：數值虛擬飛行技術對復雜運動下的飛行器動態特性、飛行器的操縱特性、控制系統參數的整定等問題的研究具有較高的工程價值和應用前景。

1　數值虛擬飛行方法

1.1流動主控方程

主控方程為非定常、可壓縮、雷諾平均的三維Navier-Stokes方程。采用來流參數為無量綱特征變量，對方程無量綱化，并將方程轉換到一般曲線坐標系下，可得如下形式[8]：

(1)

式中：Q為守恒變量向量；F、G和H為對流通量；Fv、Gv和Hv為黏性通量；Re為來流雷諾數。

采用基于結構網格的有限體積法求解，對流通量計算采用帶熵修正的Roe格式，采用MUSCL插值和vanAlbada限制器達到二階空間精度。時間推進格式在定常計算時選用隱式LU-SGS方法，在非定常計算時選用雙時間步LU-SGS格式。采用一方程的Spalart-Allmaras湍流模型計算獲得湍流渦黏性。利用基于共享內存的Open-MP并行技術加速計算。

1.2結構重疊網格技術

網格生成是數值模擬的重要部分之一，好的網格質量是獲得合理計算結果的前提條件。結構重疊網格邏輯關系簡單，魯棒性好，適合開展工程計算。在大部分計算區域，結構重疊網格計算方法同結構網格完全一樣，并能保證和結構網格相同的計算精度、計算效率及流動特性捕捉能力，而網格間的重疊技術降低了復雜拓撲外形的網格生成難度[10-12]。另一方面，虛擬模擬實際問題時，被模擬物體子部件間往往會出現相對運動，如舵面/襟翼等部件受控偏轉、飛行器脫離掛架等，結構重疊網格將各子部件劃為獨立的子區域，可有效地處理這些多體運動、分離問題[12]。求解多體、部件運動等位置或形狀隨時間變化的問題時，網格無需重新生成，各子區域網格隨部件作剛性運動，每一時間步只需要進行一次重疊過程以建立插值信息關系，相比網格重構、變形等動網格方法實現更為簡單高效，且適用于任意幅度的運動[12-13]。

1.3飛行器剛體6DOF運動方程組

飛行器或運動部件作為剛體處理,在空間中剛體運動有6個自由度(DOF)，剛體在空間的平動、轉動、位置及姿態的變化可以用6個動力學方程和6個運動學方程充分描述[14]。

剛體質心動力學方程為

(2)

式中:a和V分別為慣性系下加速度和速度矢量；P和F分別為推力和氣動力在體軸坐標系下矢量，下標b表示體軸系；G為慣性系下重力矢量；L為坐標轉換矩陣；m為質量。

慣性坐標系下質心運動學方程為

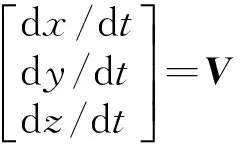
(3)

體軸坐標系下剛體繞質心轉動的動力學方程為

(4)

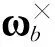
(5)

由式(4)可得體軸系下繞質心轉動的動力學方程為

(6)

再結合體軸系下角速度分量同姿態角變化關系式(7)，可獲得關于俯仰角θ、偏航角φ及滾轉角γ的剛體動力學和運動學聯立的方程組為

(7)

1.4控制系統模化

飛行控制系統一般由舵回路、穩定回路和制導回路這3個反饋回路構成。這3個回路主要實現氣動力(氣動面)控制、擔負穩定與控制功能，以及按照一定導引律給出控制指令[15]。

在數值虛擬飛行中可以使用任意的控制器，復雜的控制器的實現、考察不在本文研究范圍中。為簡化起見，本文采用PID控制器，實現舵偏反饋控制，并形成穩定的制導回路來跟蹤指定迎角變化規律。PID控制器如圖1所示。

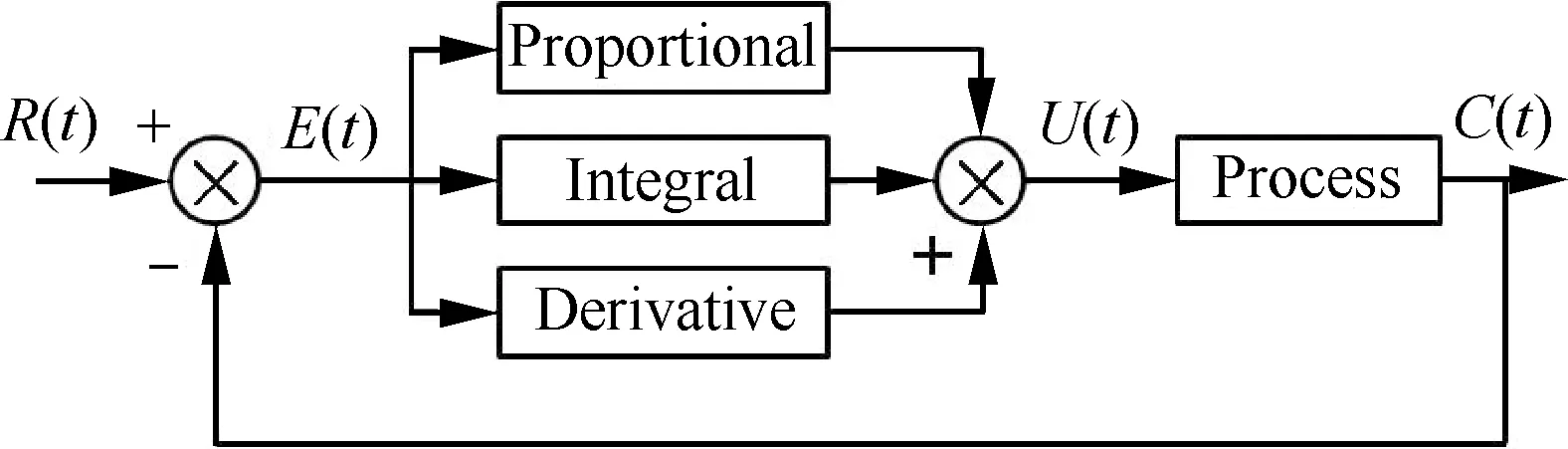
圖1　PID控制器框圖Fig.1　Block diagram of PID controller

圖中：R(t)為設定值，C(t)為檢測值，E(t)為設定值和檢測值間的偏差，可見PID控制器是通過對偏差進行運算獲得控制值U(t)。PID運算包含3部分，第1部分為比例控制Proportional，比例控制器為一個增益(放大)器，其將輸入信號放大Kp倍，Kp稱為增益(放大)系數，增加Kp可提高系統準確性，降低系統慣性，但會影響控制穩定性。第2部分為積分控制器Integral，增加積分控制器參數Ki可以減小控制系統的穩態誤差，但有可能引起系統振蕩。第3部分為比例微分控制器Derivative，改變Kd可影響系統響應速度，即影響控制系統的快速性[16]。

在模擬中，考慮到非定常CFD計算的物理時間步長遠遠小于舵機的響應時間，因此假設舵面每隔Td接受一次控制信號。在Td時間內，舵偏規律設為

(8)

式中：Δd為需要接受控制指令后舵面需要偏轉的總舵偏角；d(t)為舵偏角關于時間的函數；int為取整函數。

1.5氣動/運動/控制集成流程

數值虛擬飛行的核心流程是氣動/運動/控制(CFD/RBD/FCS)耦合求解。其中，CFD模塊采用非定常方法求解獲得每一物理時間步飛行器受到的氣動力和力矩。剛體運動(RigidBodyDynamics，RBD)模塊根據力和力矩情況，求解剛體6DOF方程，更新物體位置(網格坐標)。

本文使用松耦合算法[17]求解剛體動力學方程與流動控制方程的耦合問題，采用龍格庫塔法求解動力學方程，采用雙歐法求解飛行器姿態變化。在獲得剛體下一時刻的位移和姿態角后，由式(9)獲得n+1時刻的網格點坐標為

Rn+1=Ln+1·R0

(9)

式中：Ln+1為由n+1時刻的姿態角確定的轉換矩陣；R0為初始的網格坐標。

控制系統(FlightControlSystem，FCS)模塊根據飛行器姿態與期望的偏差形成反饋控制，結合重疊網格等動網格技術控制氣動操縱面，控制飛行器姿態。然后再反復上述過程，直到運動結束。流程如下：

1) 為減小計算時間，采用定常計算獲得初始流場。

2) 以初場為基礎開展非定常流動計算。

3) 每推進一個物理時間步，求解飛行器的氣動力和力矩，代入RBD求解獲得物體位移，更新整體網格位置。

4) 根據FCS，控制操縱面運動，更新操縱面物體(網格)位置。

5) 開展下一物理時間步流場計算，重復步驟2～5，直至物理時間推進結束。

2　數值方法驗證

用三維的超聲速彈道外形[18](HyperBallisticShape，HBS)對程序和方法的正確性和可信度進行驗證。HBS外形如圖2所示，具有試驗數據可供對比，是一個廣泛用于超聲速動態非定常計算程序驗證的標準算例。

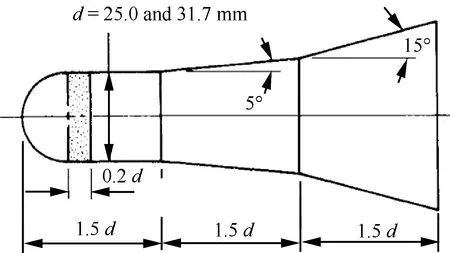
圖2　超聲速彈道模型外形及尺寸Fig.2　Shape and size of HBS model

采用文獻[18]中來流參數開展計算，具體為：來流馬赫數6.85，質心在彈長0.72倍處，以前段直徑d為特征長度的雷諾數為0.72×106。對比在0°、5°、10°、15°和20° 迎角下計算和試驗獲得的俯仰導數，俯仰動導數采用振幅為1° 的正弦強迫運動計算獲得，強迫運動的減縮頻率取0.01，計算物理時間步長為2ms。圖3(a)為計算獲得的靜導數Cmα同試驗值對比，程序準確計算出了約在8° 迎角附近導數符號的改變。圖3(b)為俯仰動導數同試驗值對比，計算同試驗數據符合較好，表明本文程序和非定常方法是可行的。

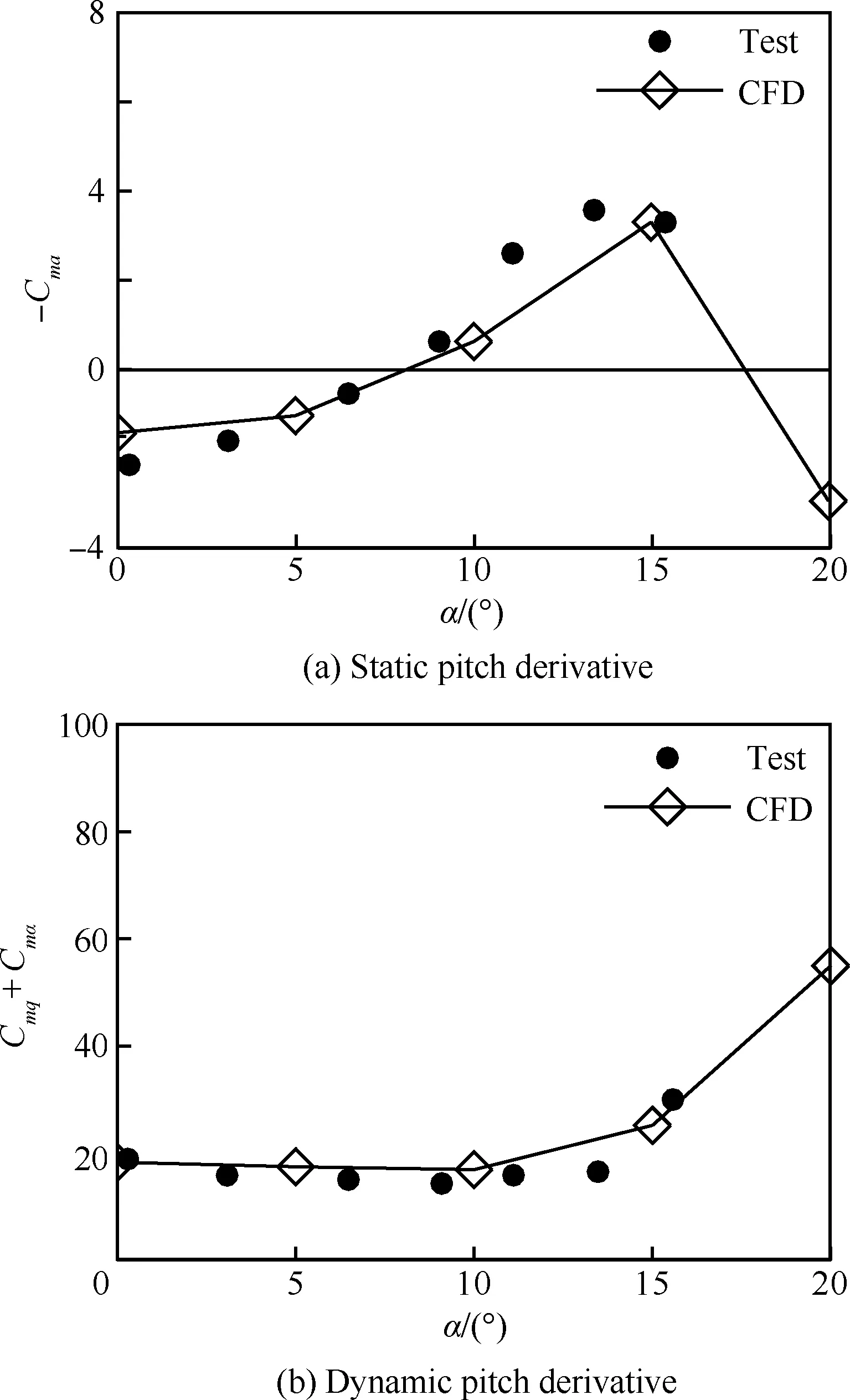
圖3　HBS俯仰靜、動導數計算與試驗數據對比Fig.3　Comparison of computational static and dynamic pitch derivative with test data of HBS

3　數值模擬結果及分析

3.1返回艙外形平面運動動態特性研究

起源號返回艙網格如圖4所示，具體外形尺寸見文獻[19]，模型物理參數見表1。

圖4　起源號返回艙表面及對稱面網格Fig.4　Surface and symmetry plane grid of Genesis capsule

表1　起源號返回艙模型物理屬性

Table 1　Physical property of Genesis capsule model

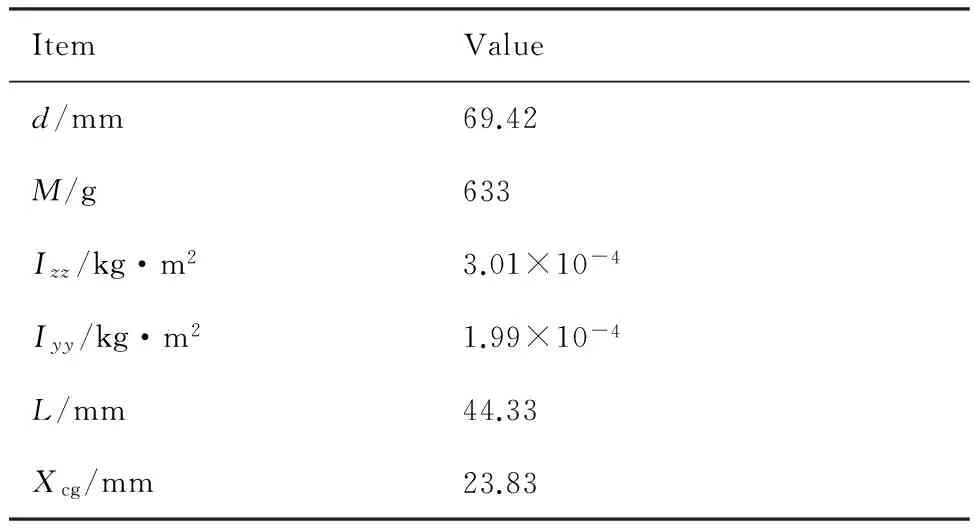
ItemValued/mm69.42M/g633Izz/kg·m23.01×10-4Iyy/kg·m21.99×10-4L/mm44.33Xcg/mm23.83

圖5為初始馬赫數Ma0為4.5，釋放迎角為0.5° 時返回艙總迎角隨射程變化規律同文獻數據對比。由圖可見，該狀態彈道的前段總迎角較小，在120 m后迎角開始發散，計算也出現了相同的趨勢。需要說明的是，文獻中并未說明返回艙釋放的角速度，計算時設初始角速度為零，從結果來看這不會對后段彈道迎角發散這一規律產生較大影響。圖6為Ma=3.5，大氣參數為海平面時，采用CFD自由振蕩計算獲得的動導數同文獻[19]中數據對比。計算結果同文獻數據接近，符合該返回艙在馬赫數大于2.5時在大迎角下為動穩定的結論。

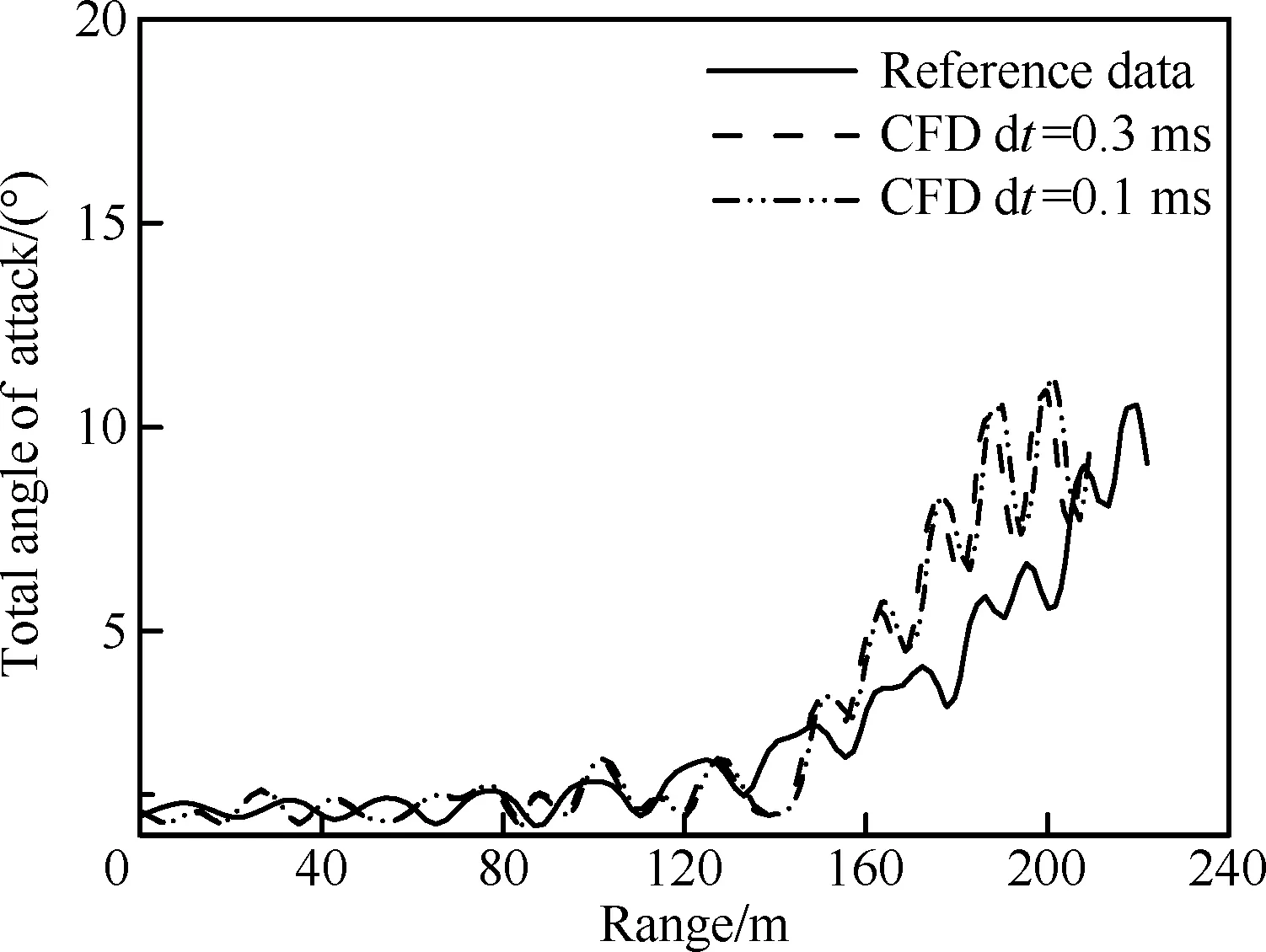
圖5　Ma0=4.5，釋放迎角為0.5° 時，返回艙總迎角隨彈道變化規律計算與試驗對比Fig.5　Comparison of computational trajectory history of total angle of attack with test data at Ma0=4.5 and release α=0.5°

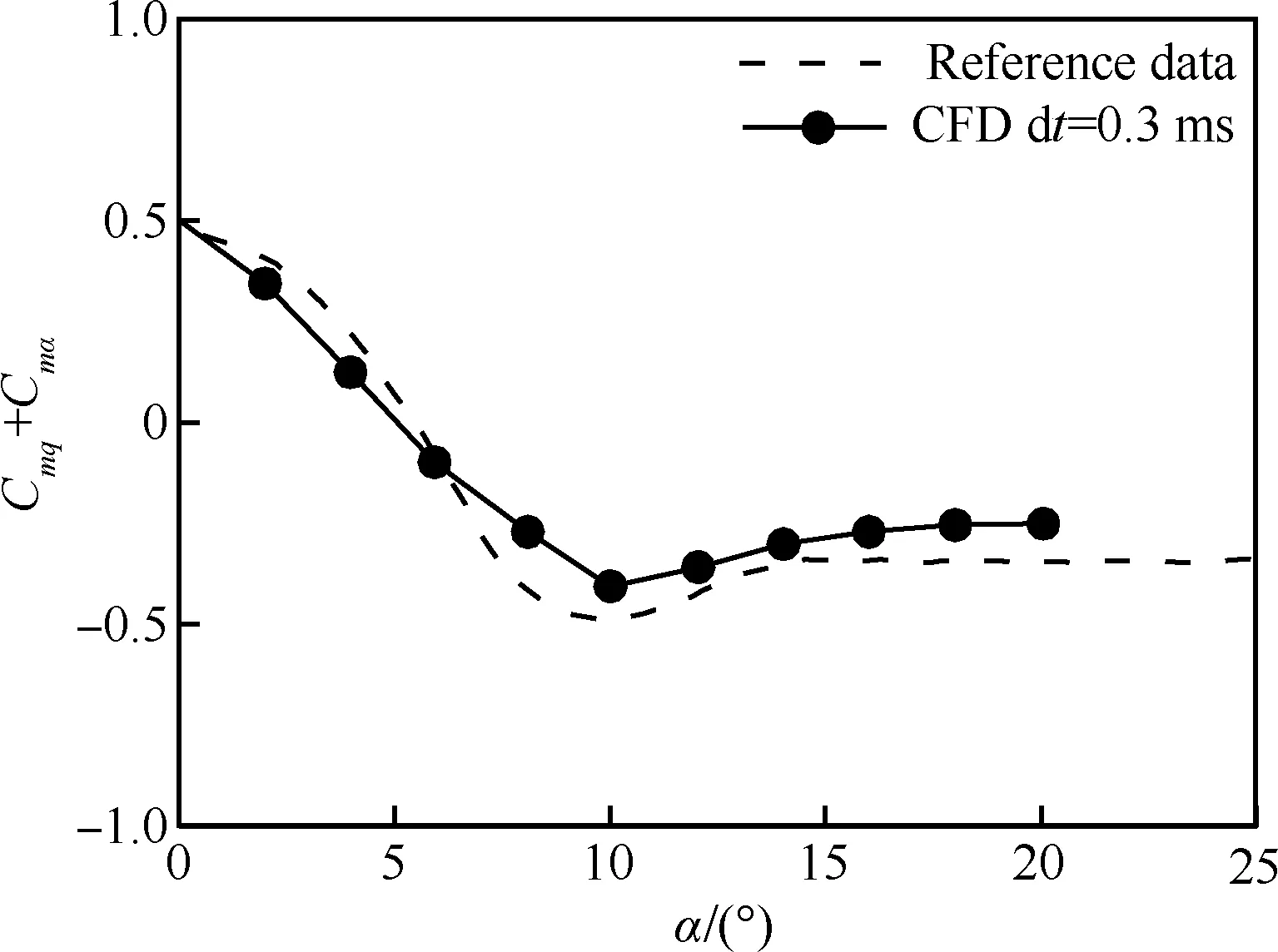
圖6　Ma=3.5時，返回艙俯仰動導數計算同文獻對比Fig.6　Comparison of computational capsule dynamic pitch derivative with reference data at Ma=3.5

以上計算結果同試驗結果吻合良好，可確定本文方法的正確性。下面的研究主要關注不同自由度運動對返回艙運動特性的影響，因此本外形算例來流參數統一為：來流馬赫數為3.5，飛行高度為25 km，來流壓力、溫度根據地球大氣參數表獲得，計算皆采用層流假設，物理時間步長統一取為0.3 ms。由于自由俯仰運動時，該系統是自治系統，其極限環狀態(振幅和頻率)與初值無關，因此，為了較快出現極限環運動，計算預置10° 迎角，并且設置返回艙的質量為表1中的1/4，以減小慣量，使運動迅速出現振蕩，以節約計算時間。

3.1.1平面單自由度俯仰運動

當返回艙繞質心做單自由度俯仰振動時，其動力學方程為

(10)

在某迎角的小的鄰近范圍內，可以假設俯仰靜、動導數為常量，則式(10)為一典型的二階阻尼系統，其解析解為

(11)

式中：ξl為阻尼；ωl為振動頻率，具體表達式為

(12)

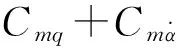
圖7為返回艙的靜、動導數隨迎角變化情況。由圖可見，各迎角下該外形靜導數變化不大，而動導數在小迎角處是正值，表現為動不穩定；迎角大于5° 后，動導數變為負值，表現為動穩定。因此，返回艙在小迎角下受到擾動，由于動不穩定性，擾動振幅將增大，在大迎角時，氣流起阻尼作用，從而衰減振幅。在一定條件下，這樣的動導數變化規律可使得飛行器出現俯仰極限環振蕩狀態。

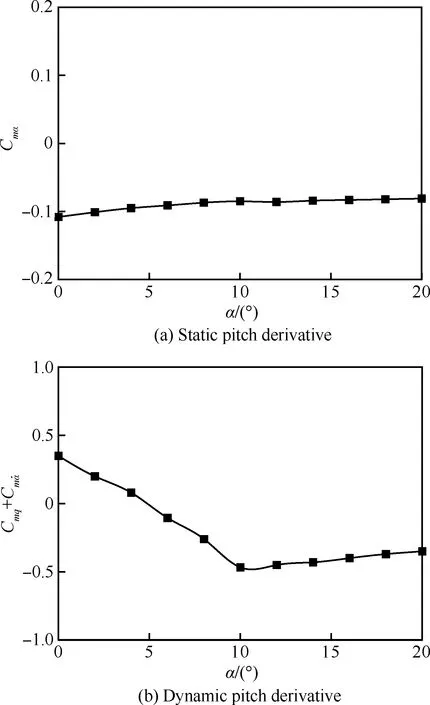
圖7　“起源號”返回艙各迎角下俯仰靜、動導數Fig.7　Static and dynamic pitch derivative of Genesiscapsule under different angles of attack

圖8為自由俯仰振蕩迎角隨時間的變化規律。可見，由前述動導數特性，從10° 迎角釋放外形后，飛行器振幅逐漸增加，當振幅達到15° 左右時，飛行器出現等周期的極限環振蕩。

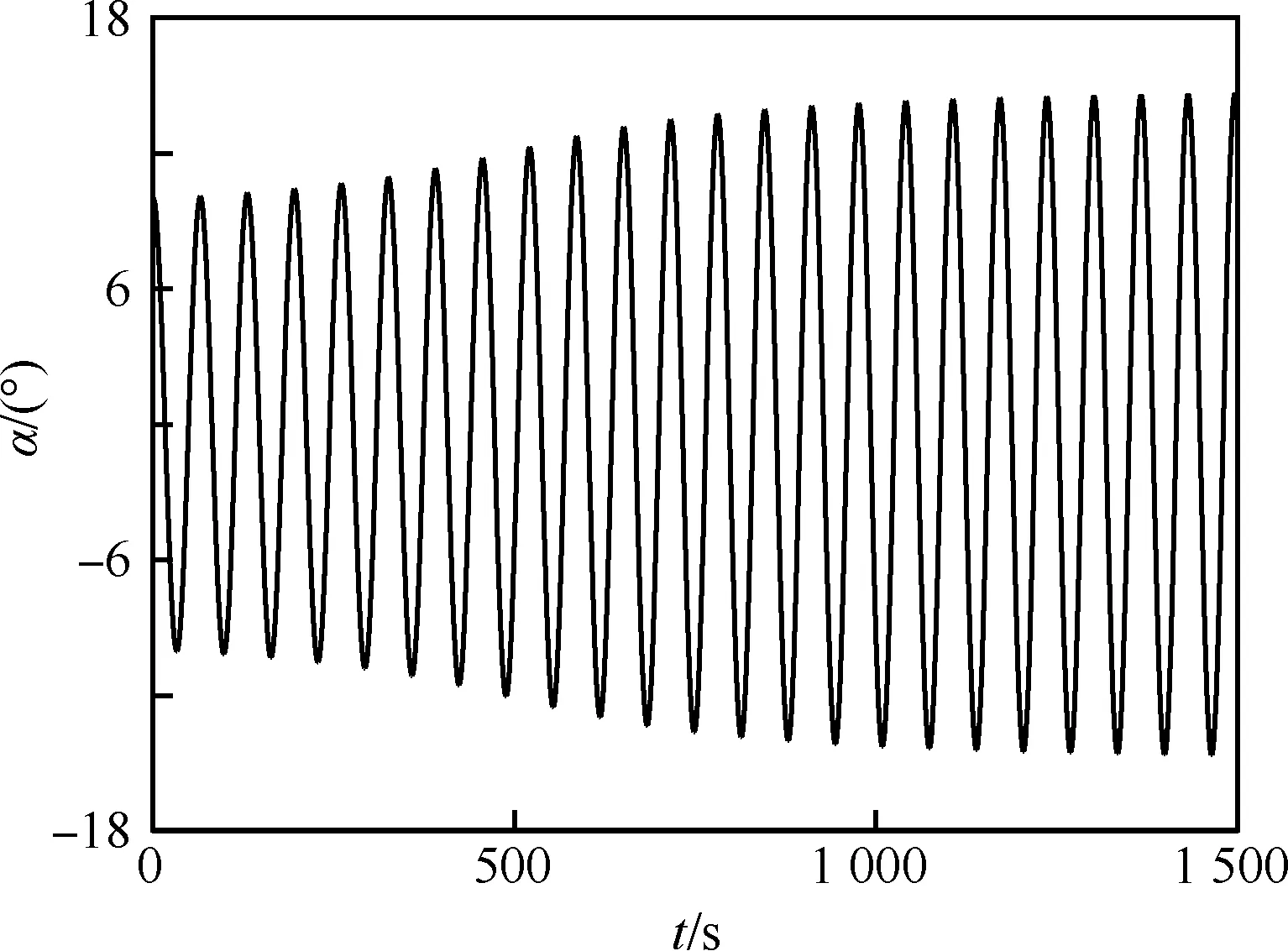
圖8　自由俯仰運動迎角隨時間變化規律Fig.8　Time history of angle of attack of free pitching motion

3.1.2平面俯仰+沉浮雙自由度運動

下面研究引入質心沉浮運動后，返回艙的運動特性。圖 9為雙自由度和單自由度運動下飛行器迎角隨時間變化規律。由圖可見，引入沉浮運動后，返回艙仍形成等周期和振幅極限環俯仰振動，但相比單自由度振動，其振幅加大，頻率減小。

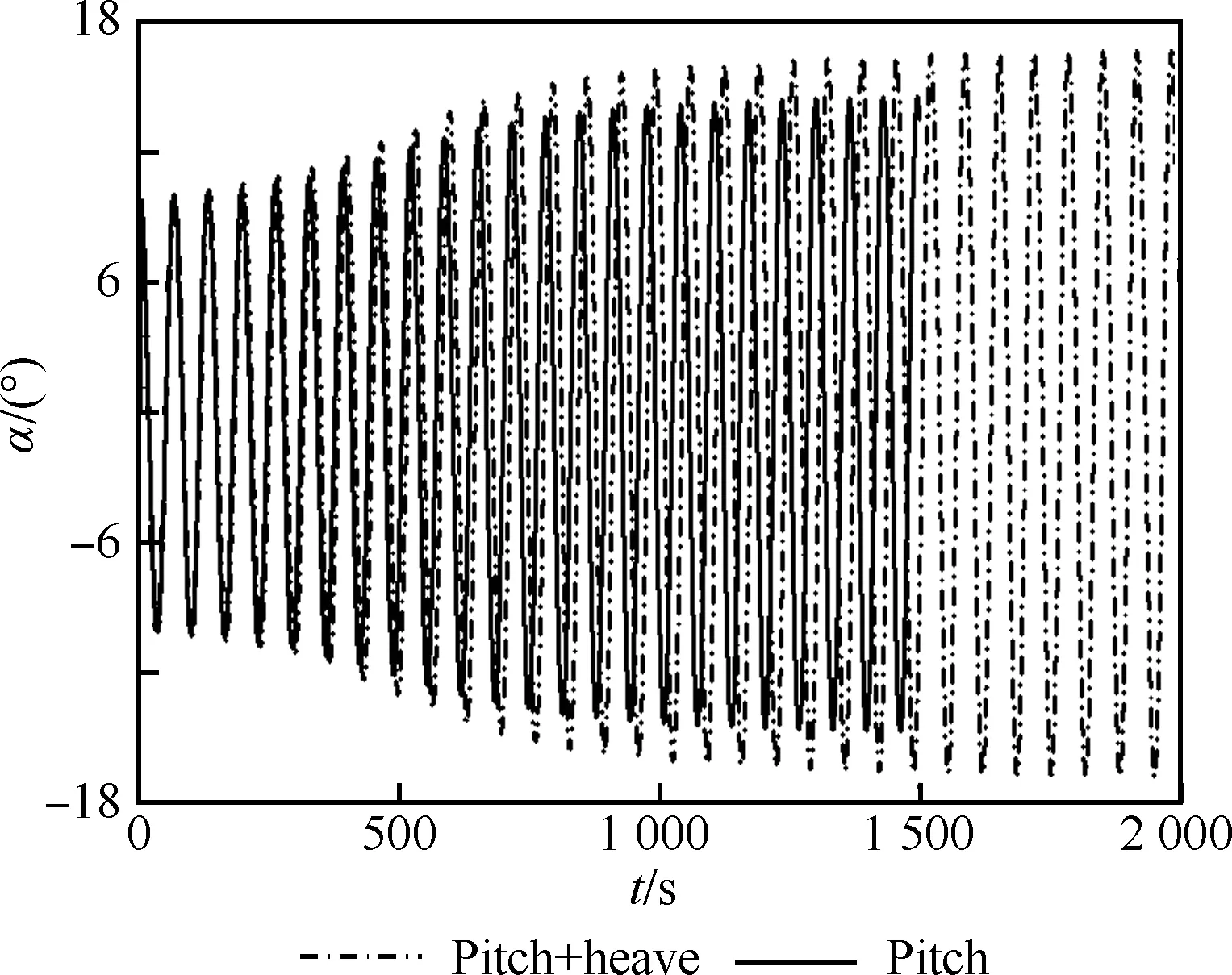
圖9　雙自由度和單自由度運動下迎角隨時間變化規律的對比Fig.9　Comparison of time histories of angle of attack of one and two DOF motion

圖10為返回艙質心沉浮速度V隨時間變化規律，其與迎角隨時間變化有1/4周期的相位差。此外，注意到，由沉浮運動引起的迎角變化不會超過0.02°，這表明引起俯仰振動頻率和振幅變化的主要原因并不是沉浮速度，而是引入沉浮運動后，系統阻尼變小導致的，這跟文獻中理論分析一致[20-21]。返回艙平面雙自由度運動下的俯仰靜、動導數及失穩特性和單自由度運動的類似，在此不再贅述。

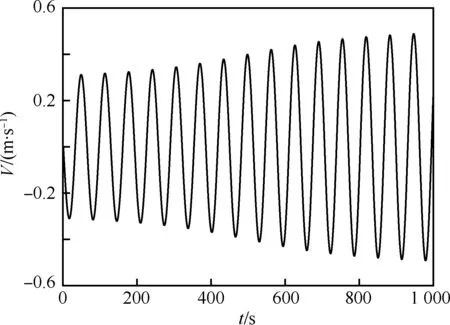
圖10　返回艙雙自由度運動質心沉浮速度隨時間的變化規律Fig.10　Time history of centroid velocity of two DOF motion of return capsule

3.1.3平面自由飛三自由度運動

返回艙返回時，在氣動阻力的作用下減速運動，引入流向運動自由度，即可考察返回艙平面自由飛行的動態特性，這種自由飛更加接近真實飛行情況。圖11為平面自由飛運動下飛行器迎角隨時間的變化規律。由圖可見，考慮氣動阻力后，返回艙振幅更大，這表明飛行器變得更為動不穩定。此外，可以看出，振蕩頻率逐漸減小，振蕩周期變長，這是由于氣動阻力使飛行器速度降低造成的。

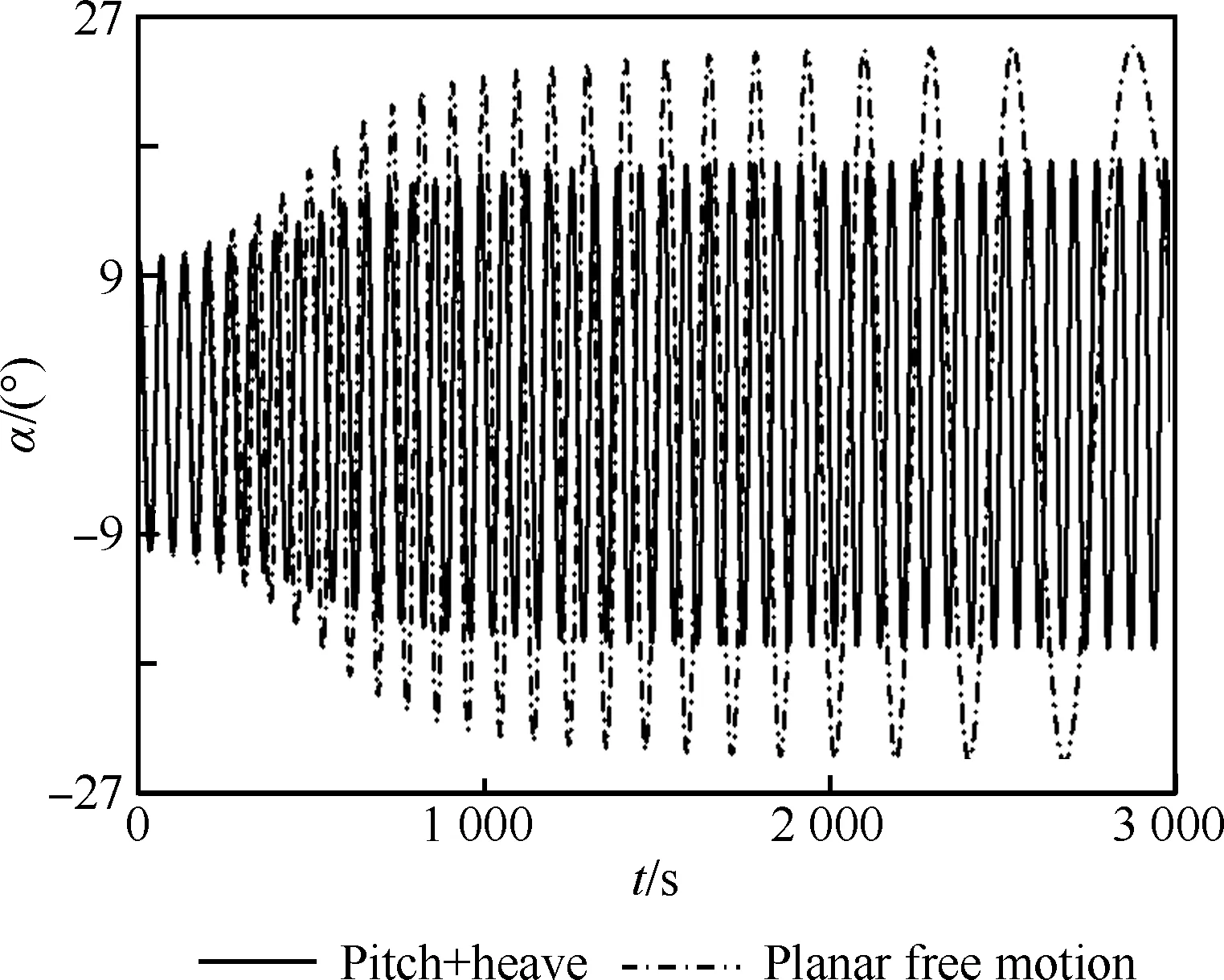
圖11　平面自由飛和雙自由度下迎角隨時間的變化規律對比Fig.11　Comparison of time histories of angle of attack of planar free and two DOF motion

圖12為平面自由飛運動下返回艙質心沉浮速度隨時間的變化規律。可見，自由飛下沉浮速度振幅比雙自由度運動下的振幅有所增加，且周期逐漸變長。圖13為質心流向速度隨時間的變化規律，空氣阻力的存在使飛行器流向速度由3.5馬赫降到了2.2馬赫左右。同樣，基于自由飛計算開展參數辨識，也可獲得相應的靜、動導數，在此不再累述。

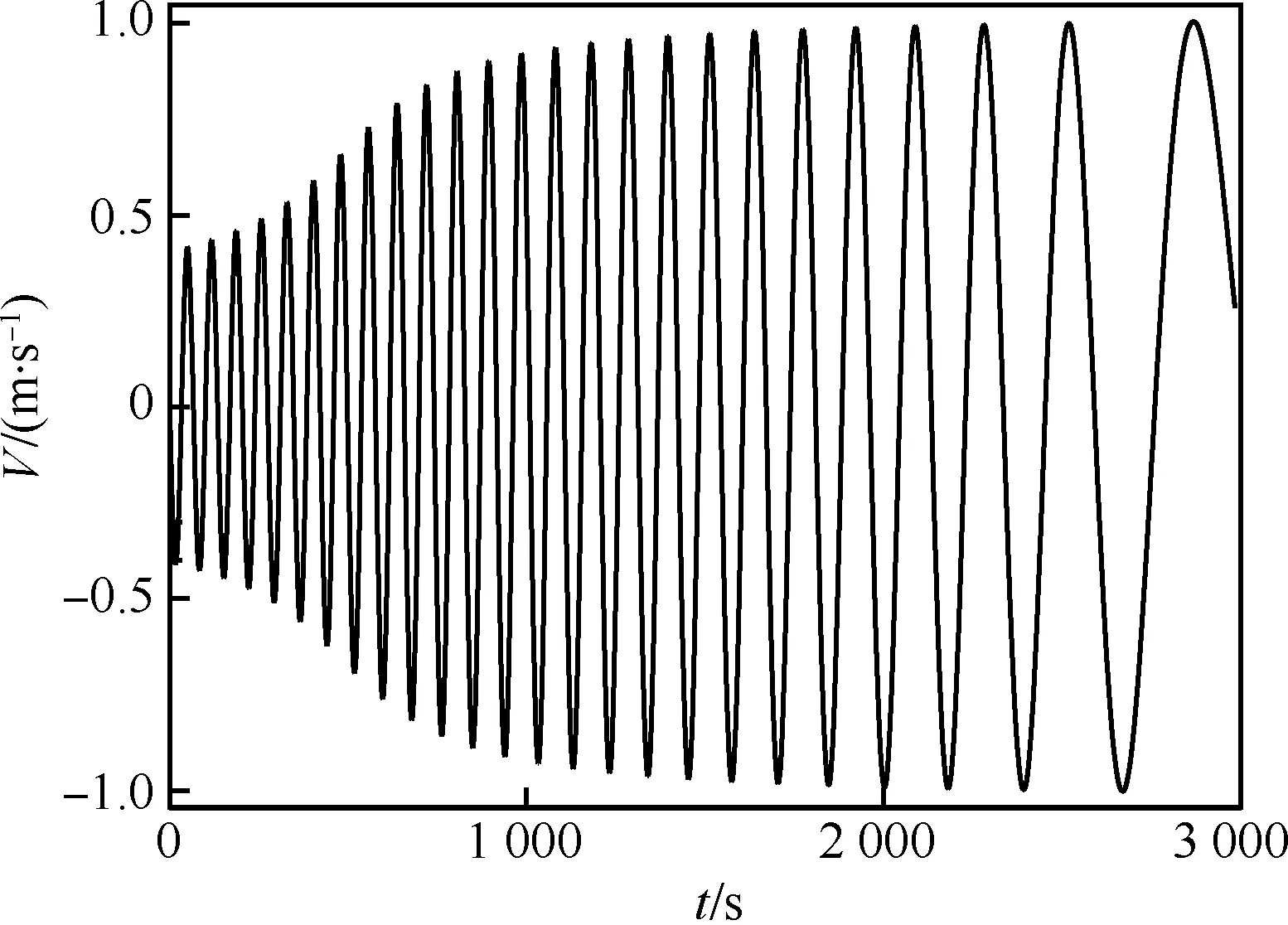
圖12　平面自由飛質心沉浮速度隨時間變化規律Fig.12　Time history of centroid velocity of planar free motion

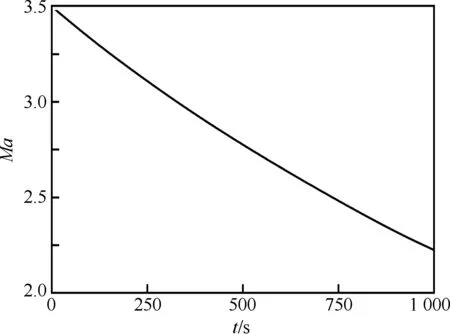
圖13　平面自由飛質心流向速度隨時間變化規律Fig.13　Time history of flow direction centroid velocity of planar free motion

3.2受控導彈縱向數值虛擬飛行模擬

計算外形為尾部安裝有4個翼的導彈。該外形具有大量的靜、動態試驗數據及計算對比數據[22-23]。該導彈外形涵蓋了大部分戰術導彈的典型氣動布局特征。導彈為十字翼布局，尾舵為均勻厚度。計算外形尺寸及舵號定義見圖14(圖中CG為模型重心)，模型物理參數見表 2。圖15為Ma=4.42，Red=2.96×107時采用不同時間步長計算獲得的俯仰角隨射程變化規律同試驗值之間的對比，其中Red是以彈身直徑d為特征長度的雷諾數；圖 16為Red=8.6×106，Ma=1.96，無量綱質心位置X/d=6.1時導彈各迎角下動導數計算與試驗對比。以上計算結果同試驗結果吻合良好，可確定本文方法的正確性。此外由圖 15可見，采用0.5 ms和1 ms時間步長的計算結果同試驗值得差異皆不大，因此為減少計算機時，之后計算中物理時間步長均取1 ms。本文只考慮俯仰通道模擬，因此只考慮1號和2號舵實現舵偏功能，舵后緣向下偏轉定義為正舵偏，采用重疊網格實現舵偏功能。此外，在下述計算皆采用一方程的Spalart-Allmaras湍流模型模擬湍流黏性，子迭代收斂殘差取為0.01。

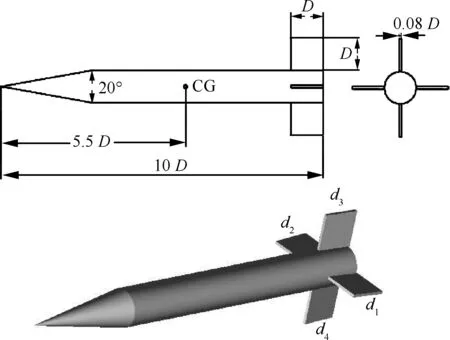
圖14　基本帶翼導彈模型外形及尺寸Fig.14　Shape and size of basic finner

表2　基本帶翼導彈計算模型物理屬性

Table 2Physical property of calculation model of basic finner

ItemValueL/m0.3M/kg1.58Ixx/kg·m21.92×10-4Iyy/kg·m297.85×10-4d/m0.03Xcg/m0.165

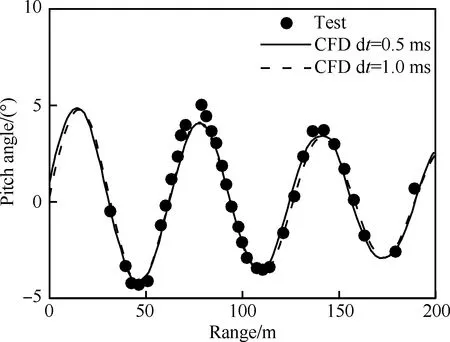
圖15　導彈俯仰角隨射程變化計算同試驗值對比Fig.15　Comparison of computational projectile pitch angle variation with range and test data

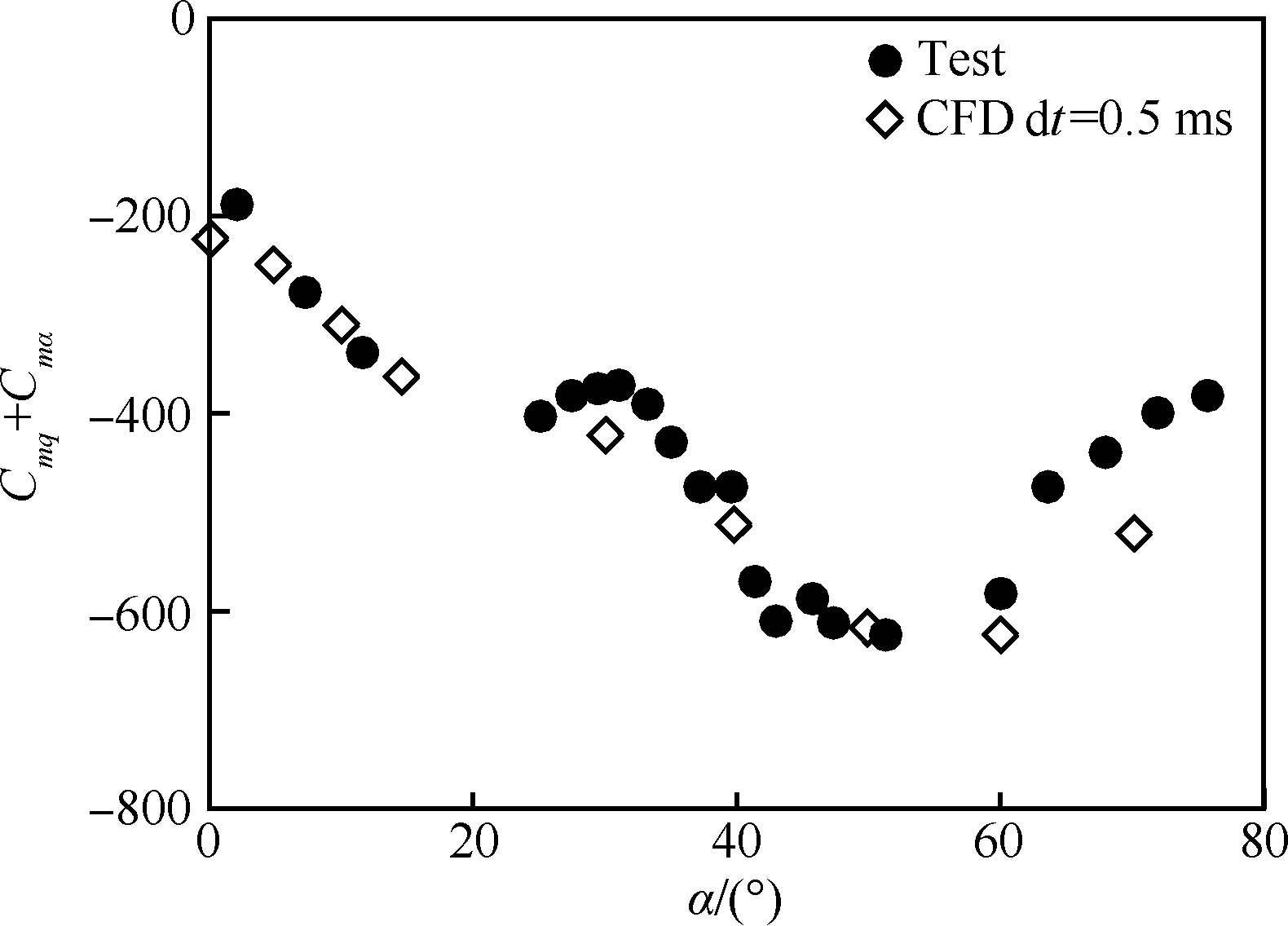
圖16　Red=8.6×106時動導數計算試驗值對比Fig.16　Comparison of computational dynamic derivative with test data at Red=8.6×106

3.2.1飛行器姿態穩定特性研究

飛行器的穩定特性包括動穩定性和動操縱性。當飛行器受外界擾動后的運動體現其動穩定性，當飛行器受操縱力控制后的運動體現其動操縱性。設計擾動規律，開展飛行器姿態穩定研究，可以檢驗飛行器不同的運動模態，測試飛行器在各種極端情況下的靜、動穩定性，且可為氣動參數辨識提供足夠的信息。

采用時域法分析一個系統的性能，一般采用一些典型的輸入作為測試信號，如階躍輸入，脈沖輸入等[16]，結合導彈飛行的特點，本文選取如下4種舵偏規律作為擾動輸入，測試基本外形導彈在不同舵偏擾動下的姿態穩定性：

1) 階躍型舵偏輸入

d(t)=5°t≥0

(13)

2) 方形脈沖舵偏輸入

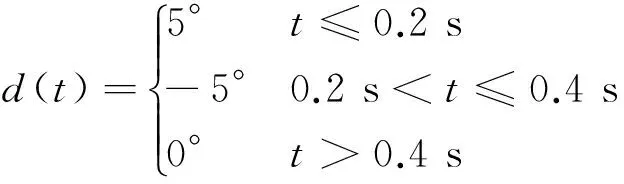
(14)

3) 梯形舵偏輸入

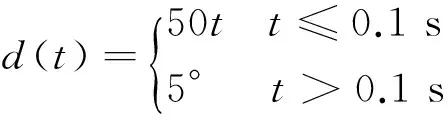
(15)

4) 正弦舵偏輸入

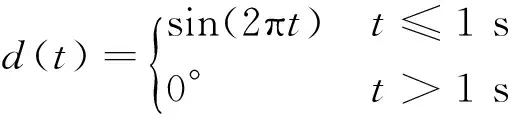
(16)

式中:d(t)為舵偏角隨時間的函數;t為物理時間。下面計算中來流條件為Ma=2，高度為10 km，來流壓力及密度根據大氣參數表獲得，飛行器初始迎角為0°,無姿態角速度及姿態角加速度。

基于小擾動理論，基本外形導彈帶舵面控制的無量綱縱向運動方程可寫為

(17)

式中：Iz為轉動慣量；θ為俯仰角。

式(17)的特征方程為

(18)

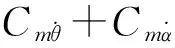
圖17為階躍舵偏下導彈俯仰角響應曲線及俯仰角速度響應曲線。階躍舵偏反映了舵偏(擾動)突變的一種極限情況，而飛行受擾動后收斂于平衡位置的過程反映了飛行的動穩定性。由圖可見，階躍舵偏(擾動)引起的角速度達200°/s左右，飛行器俯仰角振蕩收斂到-5.5° 左右，振蕩次數、幅度衰減情況反映了飛行器的操縱品質。式(17)在階躍舵偏下的解為

(19)

式中：αeq為配平攻角；φ為相位裕度，具體表達式為

(20)

結合式(18)與式(19)，即可辨識出俯仰阻尼導數等參數。

圖18為偶極脈沖舵偏下導彈俯仰角響應曲線及俯仰角速度響應曲線。在t=0.2 s時，此時導彈具有正俯仰角速度，0.2 s時刻后，舵偏變負，產生的抬頭力矩加劇了抬頭的趨勢。當干擾頻率與飛行器固有頻率接近時，可能引起飛行器共振。偶極脈沖舵偏可反映飛行器受到瞬時、隨機且頻率接近飛行器固有頻率的干擾的動態性能。

圖19為梯形脈沖舵偏下導彈俯仰角響應曲線及俯仰角速度響應曲線。梯形脈沖舵偏反映了等速舵偏與階躍舵偏的組合情況。由圖可見，此時超調量小于階躍型舵偏，且振動頻率也小于階躍型舵偏，最大俯仰角速度約為100°/s，這種舵偏規律代表了緩慢的機動飛行。

圖17　階躍舵偏下的俯仰響應曲線Fig.17　Pitch response curve of phase step impulse rudder deflexion

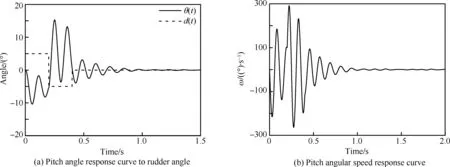
圖18　偶極脈沖舵偏下的俯仰響應曲線Fig.18　Pitch response curve of dipole impulse rudder deflexion

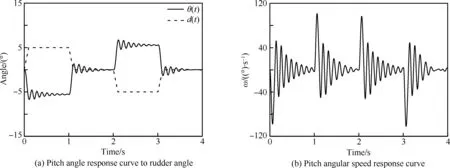
圖19　梯形脈沖舵偏下的俯仰響應曲線Fig.19　Pitch response curve of echelon impulse rudder deflexion

圖20為諧波脈沖舵偏下導彈俯仰角響應曲線及俯仰角速度響應曲線。由圖可見，此種情況下，舵偏(擾動)引起的最大俯仰角速度及俯仰力矩相對前3種情況是最小的，此時飛行器實施精確跟蹤，處于理想化的反復修正過程。

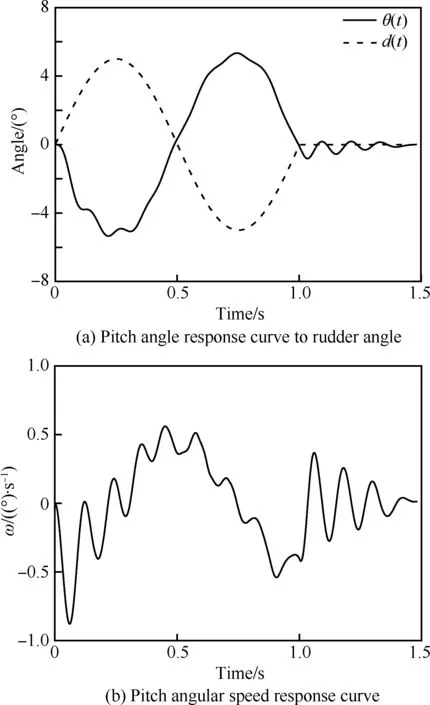
圖20　諧波脈沖舵偏下的俯仰響應曲線Fig.20　Pitch response curve of harmonic wave impulse rudder deflexion

3.2.2基于數值虛擬飛行對控制參數的整定

飛行器在飛行過程中，控制系統會根據飛行狀態發出實時控制指令，修正飛行姿態。系統受控后，要么導致受控發散，要么趨于受控狀態。飛行器是否會出現受控發散，即控制是否具有穩定性，可以采用3.3.1節中的方法檢驗。而對于受控穩定情況，則要考慮控制系統的準確性，快速性及平穩性。

控制系統的準確性，快速性及平穩性與控制系統的參數有很強的關系。同一種控制方式，面對各種各樣的飛行器，滿足上述要求的控制參數也大不相同。即使對于同一個飛行器，由于飛行過程中燃料消耗導致的質量、慣性矩及重心的物理參數的改變，也會使飛行器受控后響應發生改變。而對于處于非定常/非線性流動下的飛行器，氣動力、力矩的突變、遲滯特性更會使得基于線化氣動導數等參數獲得控制參數不能在全范圍內保證控制的穩定、準確、快速及平穩性。因此，整定控制參數，是數值虛擬飛行一個重要的應用，也是風洞等常規手段難以實現的。

本文采用PID控制器，實現舵偏反饋控制，跟蹤指定迎角規律。測試了不同PID參數(如表3 所示)下導彈的縱向受控性能，以獲得較好的控制參數。

模擬的來流條件為：Ma=2，高度為10 km，初始迎角為a=0°，初始俯仰角速度為零，角加速度也為零。導彈姿態角變化要求為：機動到5° 迎角飛行，超調不超過20%，并維持姿態穩定。按上述要求及計算模型物理屬性，根據PID控制理論[16]，選取如下范圍的PID控制參數及舵受控時間Td，對該范圍的參數整定，以達到最佳控制效果。

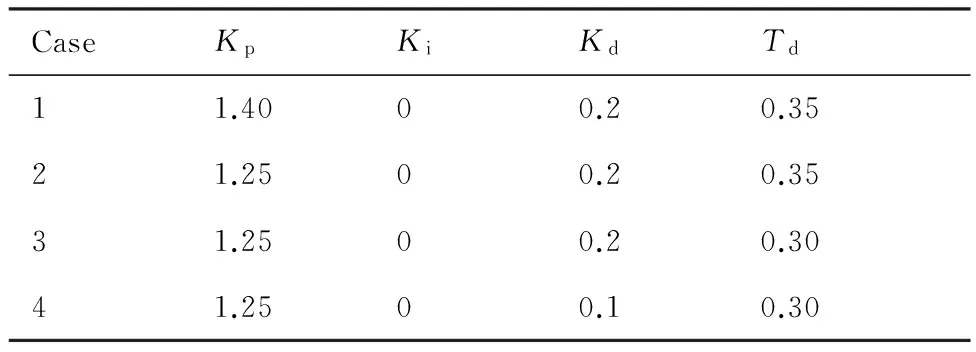
表3　PID控制參數

圖21～圖24為各控制參數下導彈的響應時間歷程。從圖中可以看到，控制系統根據飛行器姿態角的誤差發出控制指令，控制舵面，飛行器實施機動，然后反復調節，直至飛行器達到期望姿態。由相圖可見，初始階段，飛行器的俯仰角速度增加，迎角也隨之增加，當迎角接近指定值5° 時，微分控制器開始制動，減小俯仰角速度，當姿態角度超過5° 后，在控制器作用下，舵面反復調整，使得俯仰角速度變負，最后逐漸收斂于相圖上的螺旋點。

對比Case 1和Case 2可以看出，Case 1超調量約20%，Case 2超調量約10%，Case 1的最大俯仰角速率約為33°/s，而Case 2為30°/s。這表明增加Kp，會提高系統的響應速度，但會使得超調增加，振蕩過渡過程變長。對比Case 3和Case 4相圖可以看出，在迎角達到2° 左右時，控制系統開始制動，即減小俯仰角速率。制動后Case 3的最大俯仰角速率為39°/s，Case 4的最大俯仰角速率為42°/s。這表明增加Kd，使得系統的制動提前，降低俯仰角速度峰值，能減少過渡振蕩過程。對比Case 2和Case 3，Td減小加快了俯仰角速率，提高了系統響應速度。

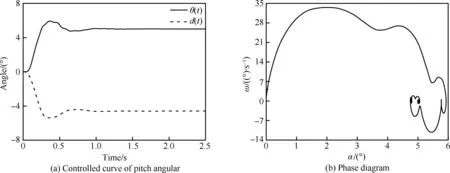
圖21　Case 1的俯仰響應曲線Fig.21　Pitch response curve of Case 1

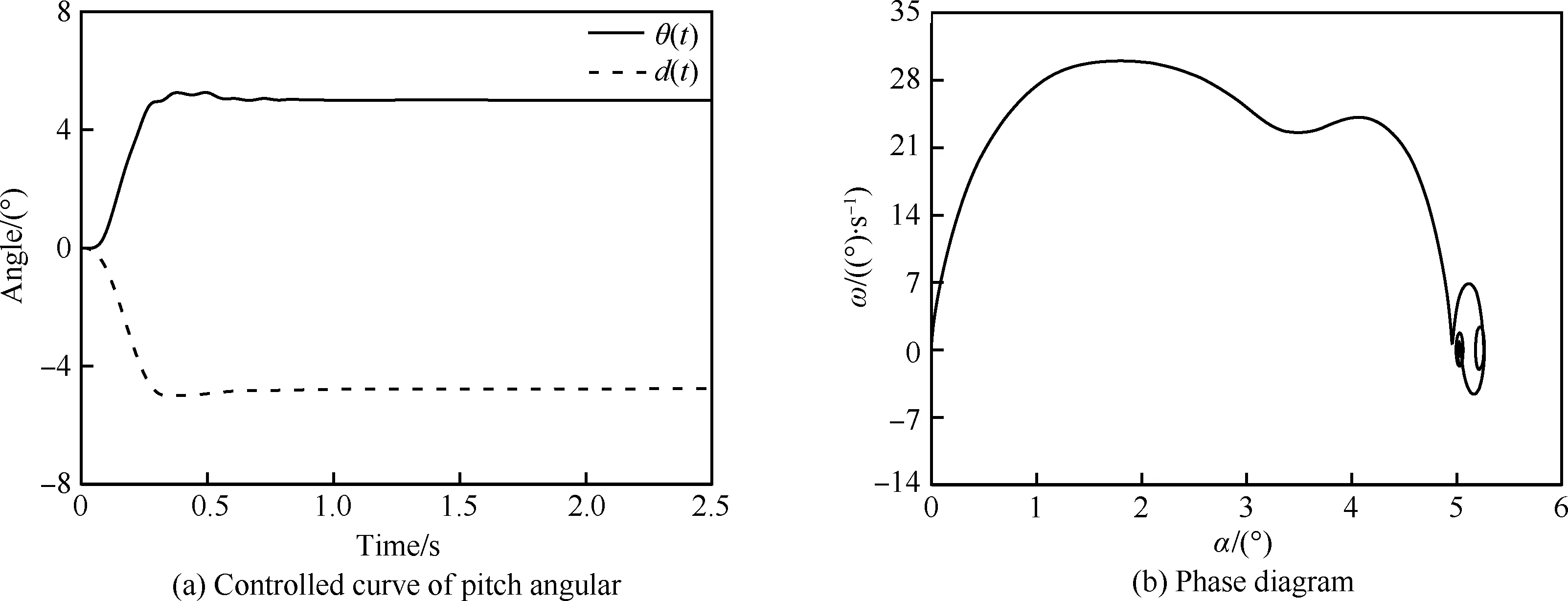
圖22　Case 2的俯仰響應曲線Fig.22　Pitch response curve of Case 2

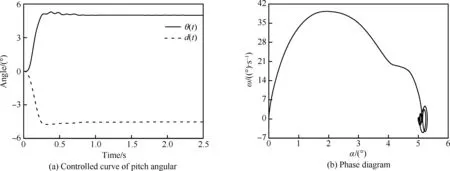
圖23　Case 3的俯仰響應曲線Fig.23　Pitch response curve of Case 3

上述算例表明，Case 3的控制參數有較好的特性。下面采用Case 3控制參數對有初始俯仰角速度的狀態進行控制，驗證控制效果，初始俯仰角速度設為50°/s。

圖25為采用Case 3的控制參數下的俯仰角控制曲線和相圖。導彈在初始俯仰角速度的作用下，迎角增加。由于導彈是靜、動穩定，且此時舵偏角較小，俯仰角速度迅速減小變為負值。當舵偏角負向變大時，產生抬頭力矩，迎角增加，然后逐漸調整到預設迎角。初始俯仰角速度的存在使得彈體動阻尼效應較為明顯，且初始角速度越大，動態效應表現越強。

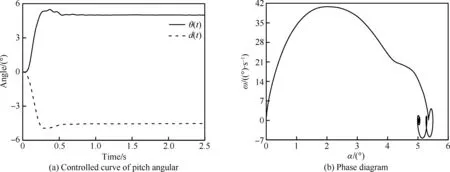
圖24　Case 4的俯仰響應曲線Fig.24　Pitch response curve of Case 4

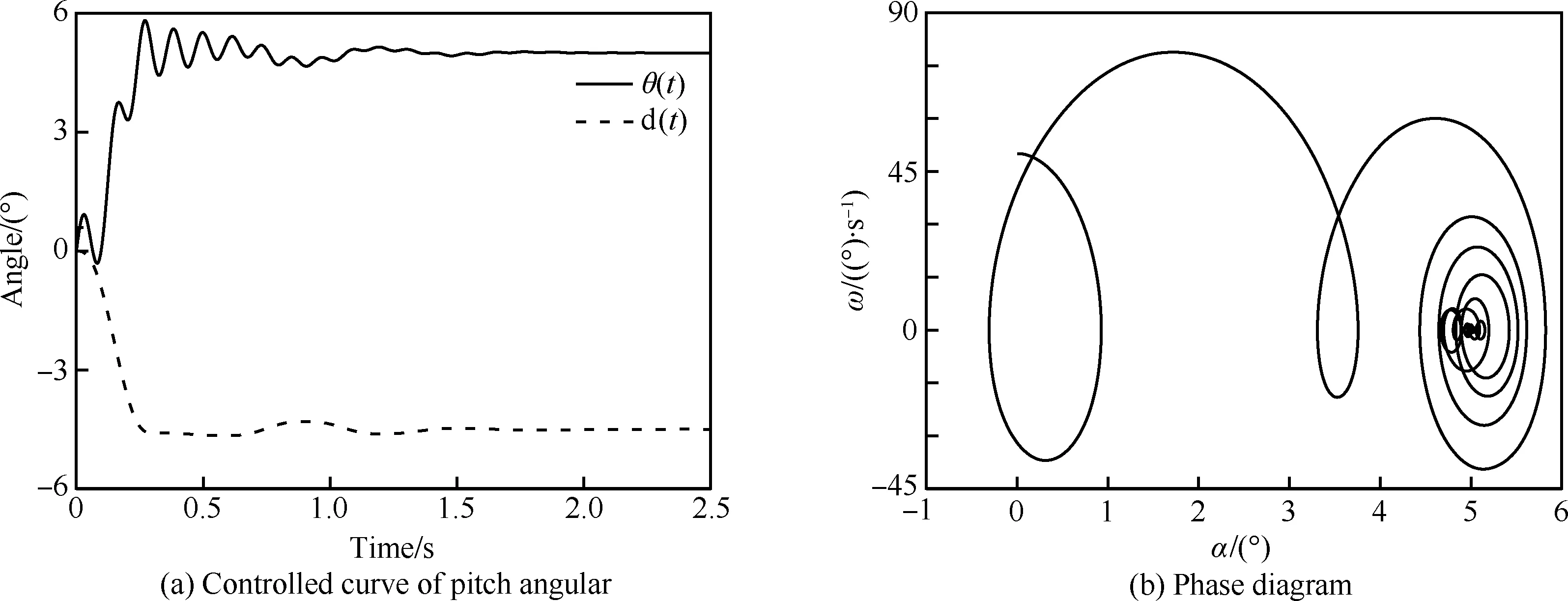
圖25　有初始俯仰角速度時的俯仰響應曲線Fig.25　Pitch response curve of state with initial pitching angular speed

4　結　論

本文利用數值虛擬飛行技術，對返回艙外形及受控基本帶翼導彈外形開展了動態特性研究。

對返回艙外形的研究表明：返回艙外形具有靜態穩定性和動不穩定性。對于平面三自由度俯仰運動，俯仰阻尼導數決定了返回艙的動穩定性。引入沉浮運動使得返回艙動穩定性變差。引入流向自由度后，氣動阻尼使飛行器速度降低，動穩定性變差，且極限環周期逐漸變長。

對受控基本外形導彈的研究表明：通過輸入典型的擾動(舵偏)信號，可以檢測導彈系統的穩定、受控性能。不同控制參數對系統的控制性能有較大影響。增大增益系數，可以提高響應速度，但會增加超調量，引起振蕩。增加微分系數，可以控制系統制動幅度及時間，減小超調量，使振蕩過渡過程盡快結束。

上述研究表明，結合結構重疊網格技術、閉環控制律的數值虛擬飛行技術能夠有效地研究常規手段無法研究的飛行器動態特性問題。其應用靈活性好，周期短，對探索飛行器氣動/運動耦合問題，控制參數的整定，控制律的研究和檢測，獲取飛行器非定常的運動導數以及飛行的安全性測試具有較好的工程應用價值及應用前景。

[1]呂光男. 風洞虛擬飛行實驗中的飛行力學與控制問題研究[D]. 南京: 南京航空航天大學, 2009： 1-13

LYU G N. The problem of flight mechanics and control in wind tunnel based virtual flight testing[D]. Nanjing: Nanjing University of Aeronautics and Astonautics, 2009:1-13 (in Chinese).

[2]李周復. 風洞特種實驗技術[M]. 北京: 航空工業出版社, 2010: 210-250.

LI Z F. Special wind tunnel testing technology[M]. Beijing: Aviation Industry Press, 2010: 210-250 (in Chinese).

[3]劉偉, 楊小亮, 趙云飛. 高超聲速飛行器加速度導數數值模擬[J]. 空氣動力學學報, 2010, 28(4): 426-429.

LIU W, YANG X L, ZHAO Y F. Numerical simulation of acceleration derivative of hypersonic aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(4): 426-429 (in Chinese).

[4]RATLIFF C L, MARQUART E J. An assessment of a potential test technique: virtual flight testing (VFT): AIAA-1995-3415[R]. Reston: AIAA, 1995.

[5]GEBERT G, KELLY J, LOPEZ J. Wind tunnel based virtual flight testing: AIAA-2000-0829[R], Reston: AIAA, 2000.

[6]MAGILL J C, CATALDI P, MORENCY J R, et al. Demonstration of a wire suspension for wind-tunnel virtual flight testing[J]. Journal of Spacecraft and Rockets, 2009, 46(3): 624-633.

[7]張來平, 馬戎, 常興華, 等. 虛擬飛行中氣動運動和控制耦合的數值模擬技術[J]. 力學進展, 2014, 44: 201410.

ZHANG L P, MA R, CHANG X H, et al. Review of aerodynamics/kinematics/flight-control coupling methods in virtual flight simulations[J]. Advances in Mechanics, 2014, 44: 201410.

[8]閻超. 計算流體力學方法及應用[M]. 北京: 北京航空航天大學出版社, 2006： 18-24.

YAN C. Computational fluid dynamics methods and applications. Beijing[M]. Beijing: Beihang University Press 2006: 18-24 (in Chinese).

[9]SALAS M D. Digital flight: The last CFD aeronautical grand challenge[J]. Journal of Scientific Computing, 2006, 28(2-3): 479-505.

[10]ROGERS S E,ROTH K,NASH S M,et al.Advances in overset CFD processes applied to subsonic high-lift aircraft: AIAA-2000-4216[R]. Reston: AIAA, 2000.

[11]GOETZ H K, JAMES E K, HENRY C L, et al. Validation of overflow for computing plume effects during the ARES I stage separation process: AIAA-2011-0170[R]. Reston: AIAA, 2011

[12]范晶晶, 閻超, 張輝. 重疊網格洞面優化技術的改進與應用[J]. 航空學報, 2010, 31(6): 1127-1133.

FAN J J, YAN C, ZHANG H. Improvement of hole-surface optimization technique in overset grids and its application[J]. Acta Aeronauticaet Astronautica sinica, 2010, 31(6)： 1127-1133 (in Chinese).

[13]袁武. 新型重疊網格方法研究及在復雜多體氣動問題中的應用[D]. 北京： 北京航空航天大學, 2012: 24-35.

YUAN W. Investigations on novel chimera grid methods and its applications to complex multibody aerodynamic problems[D]. Beijing: Beihang University, 2012: 24-35 (in Chinese).

[14]肖業倫， 航空航天器運動的建模—飛行動力學的理論基礎[M]. 北京： 北京航空航天大學出版社， 2003: 64-78.

XIAO Y L. Modeling of the motion of space vehicle—the basic of flight mechnics[M]. Beijing: Beihang University Press 2003: 64-78 (in Chinese).

[15]吳森堂, 費玉華. 飛行控制系統[M]. 北京: 北京航空航天大學出版社, 2009: 85-93.

WU S T, FEI Y H, Flight control system[M]. Beijing: Beihang University Press, 2009: 85-93 (in Chinese).

[16]MEI X R, ZHUANG X Y. Principle of auto control[M]. Beijing: Science Press, 2009: 54-61.

[17]栗長江. 高超聲速飛行器多自由度動態特性研究[D]. 長沙: 國防科學技術大學, 2010: 51-54.

LI C J. Study of mutidimensional motion of hypersonic flight vehicle[D]. Changsha: National University of Science and Technology, 2010: 51-54 (in Chinese).

[18]EAST R A, HUTT G R. Comparison of predictions and experimental data for hypersonic pitching motion stability[J]. Journal of Spacecraft, 1988, 25(3): 225-233

[19]CHEATWOOD F, WINCHENBACH G, HATHAWAY W, et al. Dynamic stability testing of the genesis sample return capsule: AIAA-2000-1009[R]. Reston: AIAA, 2000.

[20]袁先旭. 非定常流動數值模擬及飛行器動態特性分析研究[D]. 綿陽: 中國空氣動力研究與發展中心研究生部, 2002: 101-117.

YUAN X X. Numerical simulation for unsteady flowsand research on dynamic characteristicsof vehicle[D]. Mianyang: China Aerodynamics Research and Development Center. 2002: 101-117 (in Chinese).

[21]席柯. 虛擬飛行數值模擬方法及飛行器動態特性研究[D]. 北京： 北京航空航天大學, 2015.

XI K. Virtual flight numerical simulation method and research on dynamic characteristics of vehicle[D]. Beijing, Beihang University, 2015 (in Chinese).

[22]DUPUIS A D, HATHAWAY W. Aeroballistic range tests of the basic finner reference projectile at supersonic velocities: DREV-TM-9703[R]. Valcartier: Defense Research Establishment, 1997.

[23]BHAGWANDIN V A, SAHU J. Numerical prediction of pitch damping stability derivatives for finned projectiles: AIAA-2011-3028[R]. Reston: AIAA, 2011.

黃宇男， 博士研究生。主要研究方向： 計算流體力學、 混合網格數值方法。

Tel: 010-82338071

E-mail: huangyu@buaa.edu.cn

閻超男， 博士， 教授， 博士生導師。主要研究方向： 計算流體力學、 空氣動力學。

Tel: 010-82317019

E-mail: yanchao@buaa.edu.cn

Analysis of flying vehicle’s dynamic characteristics based onnumerical virtual flight technology

HUANG Yu1, YAN Chao1,*, XI Ke2, WANG Wen1

1. School of Aeronautic Science and Engineering, Beihang University, Beijing100083, China 2. Institute of Ordnance Industry Navigation and Control Technology, Beijing100089, China

With the numerical virtual flight technology based on structured overlapping grid, closed PID controller, rudder control, rigid body motion and unsteady N-S equation solver, the unsteady motion characteristic, dynamic stability and adjustment of control parameter of Genesis capsule and basic finner projectile have been simulated. The motion characteristic with different degree of freedom (DOF) motion, the motion stability and the adjustment of control parameter with disturbance of those flying vehicles have been analyzed. The calculation results show that the study of flying vehicle’s nonlinear motion under the condition of complex fluid flows can be effectively carried out by numerical virtual flight technology, which has practical value and application prospect in the area of simulation and prediction of flying vehicle’s motion and controlling characteristic, fluid mechanics study and design of control rule under the condition of unsteady and nonlinear aerodynamics.

CFD; overlapping grid; PID control; virtual flight; dynamic derivative; control parameters adjustment; dynamic characteristic; unsteady flow

2016-01-11； Revised： 2016-02-17； Accepted： 2016-04-06； Published online： 2016-04-2015:26

. Tel.： 010-82317019E-mail: yanchao@buaa.edu.cn

2016-01-11； 退修日期： 2016-02-17； 錄用日期： 2016-04-06；

時間： 2016-04-2015：26

www.cnki.net/kcms/detail/11.1929.V.20160420.1526.004.html

.Tel.： 010-82317019E-mail:yanchao@buaa.edu.cn

10.7527/S1000-6893.2016.0120

V211.3

A

1000-6893(2016)08-2525-14

引用格式： 黃宇， 閻超， 席柯， 等． 基于數值虛擬飛行技術的飛行器動態特性分析[J]． 航空學報, 2016, 37(8): 2525-2538. HUANG Y, YAN C, XI K, et al. Analysis of flying vehicle’s dynamic characteristics based on numerical virtual flight technology[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2525-2538.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160420.1526.004.html