影響Czerny-Turner結(jié)構(gòu)像散校正的因素
董科研,李欣航,2*,安 巖
(1.長春理工大學(xué) 空間光電技術(shù)研究所,吉林 長春 130022;2.長春理工大學(xué) 光電工程學(xué)院,吉林 長春 130022)
?
影響Czerny-Turner結(jié)構(gòu)像散校正的因素
董科研1,李欣航1,2*,安巖1
(1.長春理工大學(xué) 空間光電技術(shù)研究所,吉林 長春 130022;2.長春理工大學(xué) 光電工程學(xué)院,吉林 長春 130022)
針對寬波段Czerny-Turner結(jié)構(gòu)像散校正存在的問題,分析了影響光學(xué)系統(tǒng)像散校正的主要因素。基于發(fā)散光束照射平面光柵的像差理論,應(yīng)用Matlab軟件模擬分析了光學(xué)系統(tǒng)產(chǎn)生像散的原因和相應(yīng)抑制方法的不足。討論了了準(zhǔn)直鏡離軸角與聚焦鏡離軸角的角度差值α和光學(xué)系統(tǒng)像散S之間關(guān)系,理論模擬了α取不同值時(shí),寬波段C-T結(jié)構(gòu)的全波段像散校正情況。為了驗(yàn)證理論分析的正確性,設(shè)計(jì)了光譜段為900~1 700 nm的消像散型光學(xué)系統(tǒng),利用光學(xué)設(shè)計(jì)軟件Zemax對該波段的光學(xué)系統(tǒng)進(jìn)行了光線追跡和設(shè)計(jì)優(yōu)化,并對設(shè)計(jì)結(jié)果進(jìn)行處理和分析。結(jié)果顯示:隨著角度差值的逐漸增大,短波波段像散校正能力越來越強(qiáng),像散校正能力提高了1.6倍左右;長波波段像散束縛能力越來越弱,像散校正能力平均降低了1.27倍左右。得到的結(jié)果表明:角度差值的合理選取可以為寬波段Czerny-Turner結(jié)構(gòu)的像散校正提供理論指導(dǎo)。
光學(xué)設(shè)計(jì);Czerny-Turner結(jié)構(gòu);像散校正;邊緣波段
1 引 言
Czerny-Turner(C-T)結(jié)構(gòu)型光譜儀是采用平面光柵作為分光元件的光學(xué)儀器,能夠獲取物質(zhì)的光譜信息,為物質(zhì)檢測識(shí)別工作提供依據(jù)。C-T結(jié)構(gòu)具有結(jié)構(gòu)簡單、分辨能力高、色散均勻、有效避免二次和多次衍射等優(yōu)點(diǎn)。在天文學(xué)、物理學(xué)、生物學(xué)和化學(xué)等基礎(chǔ)科學(xué)領(lǐng)域,光譜儀是常用的分析儀器;在工業(yè)和農(nóng)業(yè)領(lǐng)域,光譜儀已經(jīng)成為不可缺少的檢測設(shè)備;在藥物研制、環(huán)境保護(hù)和食品安全等領(lǐng)域,光譜儀可以實(shí)現(xiàn)在線實(shí)時(shí)的定性檢測[1-4]。
像散是C-T結(jié)構(gòu)光譜儀的主要像差。目前,抑制像散的主要方法有超環(huán)面聚焦鏡[5]、自由曲面鏡[6]、傾斜柱鏡[7]、自由曲面柱鏡[8]、楔形柱鏡[9]、柱面反射鏡[10]、一階消像散方法[11]等。然而隨著光譜儀的設(shè)計(jì)波段加寬,這些光譜儀校正方法均存在一定的局限性,即邊緣波段像散的校正能力不足。為解決寬波段設(shè)計(jì)的難題,本文分析了結(jié)構(gòu)中影響像散的主要因素,主要體現(xiàn)在準(zhǔn)直鏡離軸角和聚焦鏡離軸角對系統(tǒng)的影響,從而為寬波段消像散光譜儀設(shè)計(jì)提供了理論依據(jù)。
2 像散理論
C-T結(jié)構(gòu)的像散產(chǎn)生原因是光線離軸入射球面反射鏡(準(zhǔn)直鏡和聚焦鏡),導(dǎo)致子午光束和弧矢光束的會(huì)聚能力不同,使得子午焦點(diǎn)和弧矢焦點(diǎn)分開的距離,如圖1所示,成像光束在像面上形成一系列彌散斑。像散的存在不僅影響探測器對光束能量的接收,而且抑制光譜儀空間分辨率的提高,因此,分析C-T結(jié)構(gòu)光譜儀的像散是十分必要的。
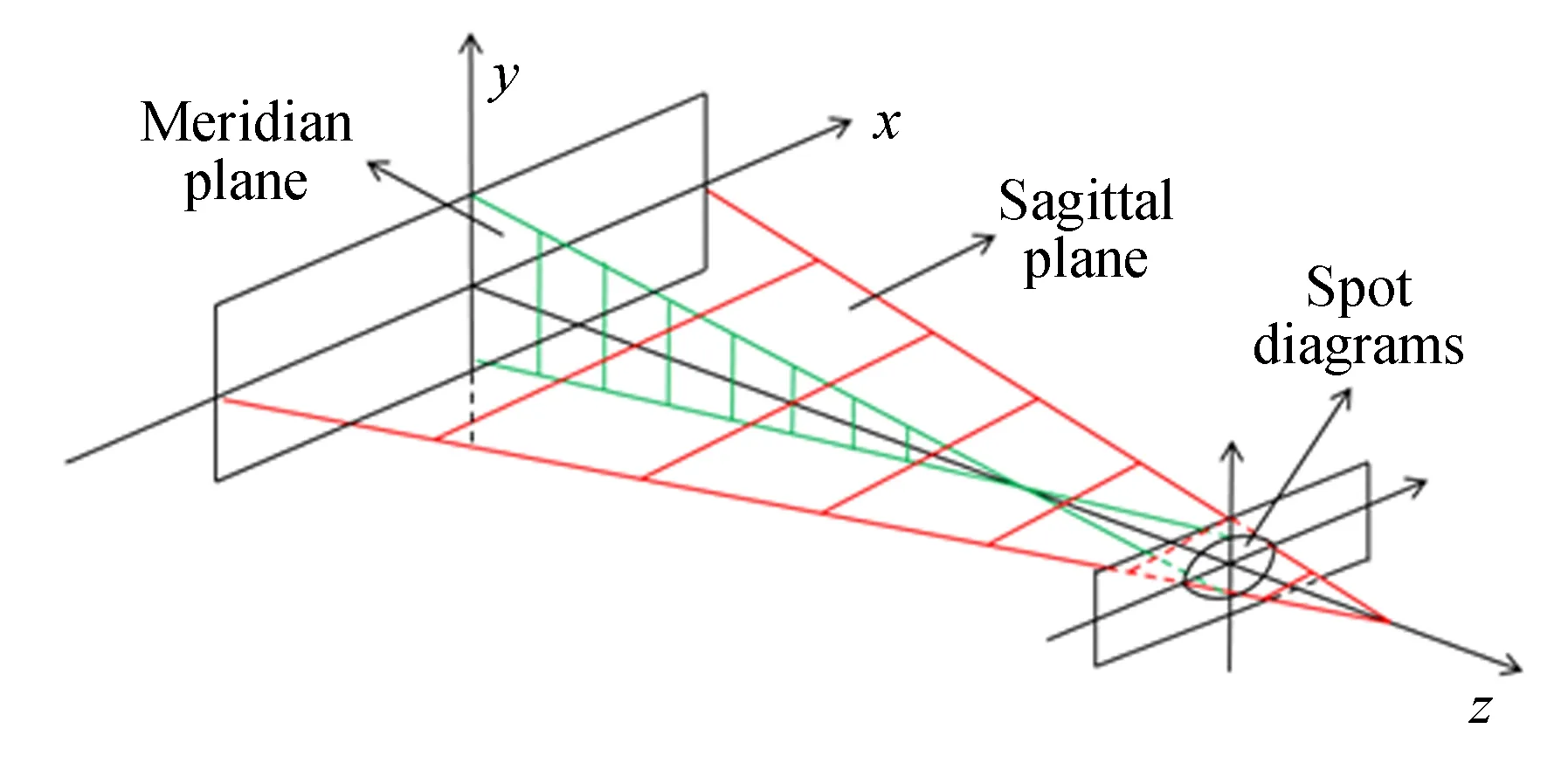
圖1 像散產(chǎn)生原理圖Fig.1 Production schematic of astigmatism
傳統(tǒng)C-T結(jié)構(gòu)由狹縫、準(zhǔn)直鏡M1、平面光柵、聚焦鏡M2和探測器組成,如圖2所示。其中α1為準(zhǔn)直鏡離軸角,α2為聚焦鏡離軸角,i為平面光柵入射角,θ為平面光柵衍射角,σ為探測器傾角(探測器與垂直平面夾角)。光源發(fā)出的復(fù)色光通過狹縫進(jìn)入光學(xué)系統(tǒng),經(jīng)準(zhǔn)直鏡第一次成像。由于準(zhǔn)直鏡離軸,導(dǎo)致弧矢像點(diǎn)和子午像點(diǎn)分開,根據(jù)細(xì)光束弧矢焦點(diǎn)和細(xì)光束子午焦點(diǎn)的位置公式,可以推導(dǎo)出準(zhǔn)直鏡的弧矢像距l(xiāng)s1和子午像距
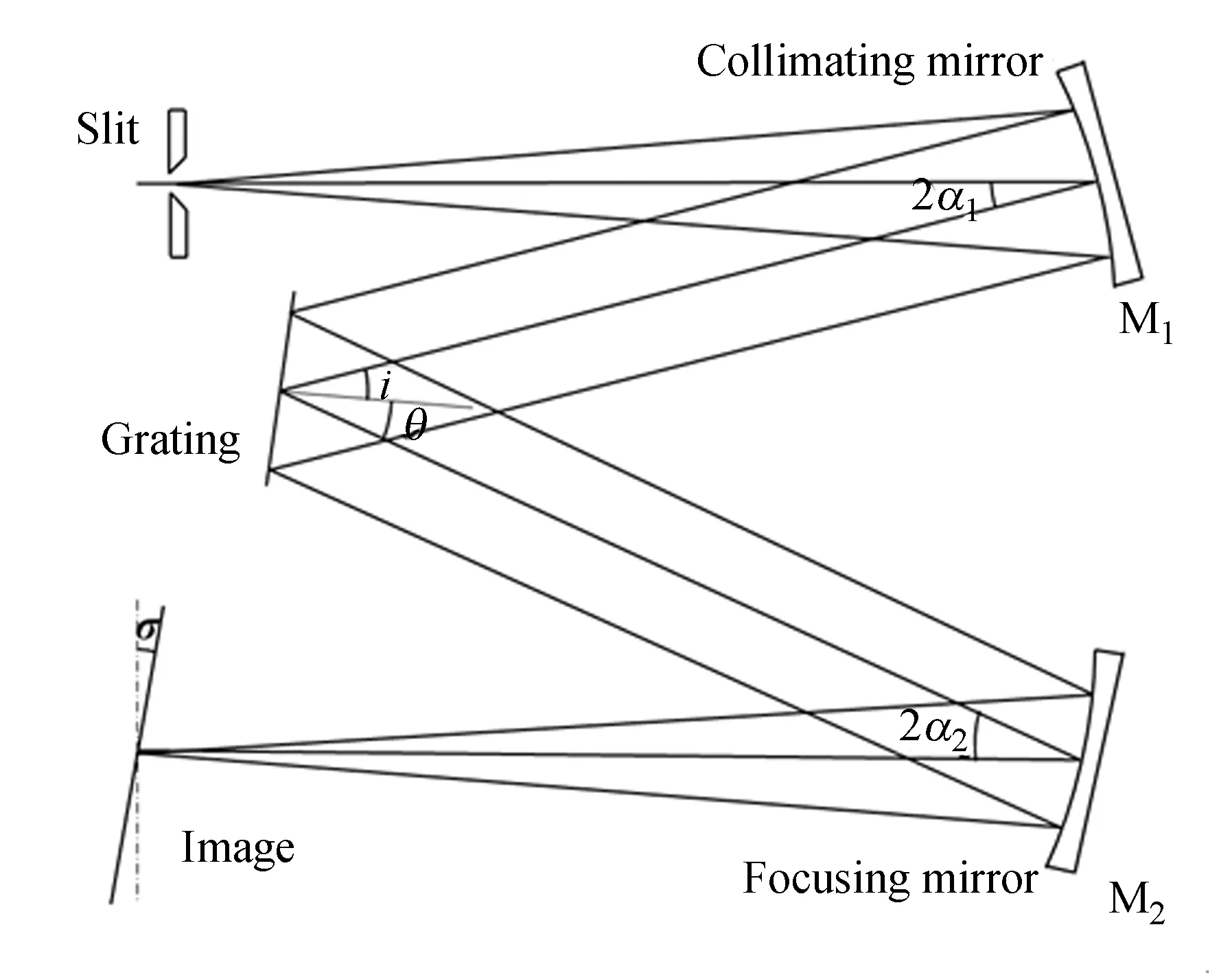
圖2 傳統(tǒng)C-T結(jié)構(gòu)原理圖Fig.2 Schematic diagram of conventional C-T structure
lt1,即有:
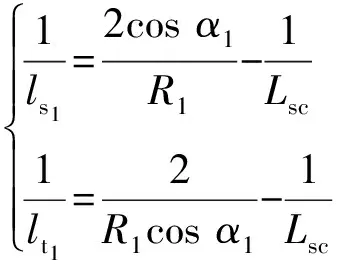
(1)
其中:R1為準(zhǔn)直鏡的曲率半徑,Lsc為狹縫與準(zhǔn)直鏡之間的距離。
經(jīng)準(zhǔn)直鏡成像后的平行光束射向平面光柵,平面光柵在C-T結(jié)構(gòu)中起分光作用,將入射的復(fù)色光分解為單色光譜。同理,可以推導(dǎo)出其弧矢像距l(xiāng)s2和子午像距l(xiāng)t2,即:
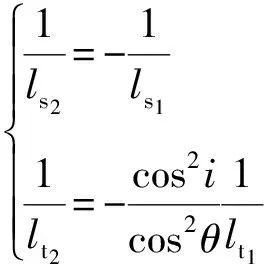
(2)
平面光柵分解后的單色光譜同時(shí)射向聚焦鏡,經(jīng)離軸聚焦鏡成像,生成相應(yīng)的弧矢像距l(xiāng)s3和子午像距l(xiāng)t3,即:
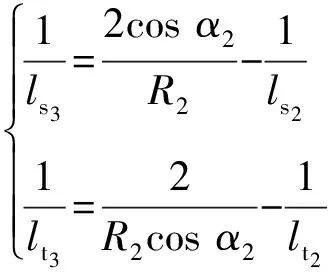
(3)
其中R2為聚焦鏡的曲率半徑。
經(jīng)準(zhǔn)直鏡、平面光柵和聚焦鏡成像后的光束,最終會(huì)聚在探測器上,形成一系列按波長排列的單色連續(xù)光譜。聯(lián)立式(1)、式(2)和式(3),得到光學(xué)系統(tǒng)的弧矢像距Ss和子午像距St為:
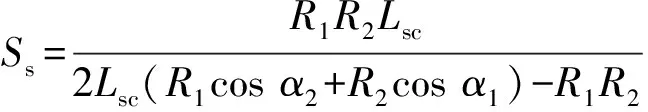
(4)

(5)
令聚焦鏡離軸角與準(zhǔn)直鏡離軸角的角度差值為α,即α=α2-α1,將α2=α+α1帶入式(4)和式(5),可得:
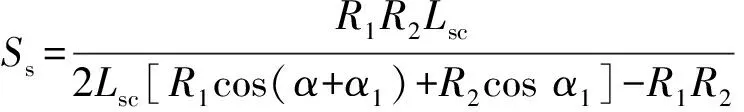
(6)
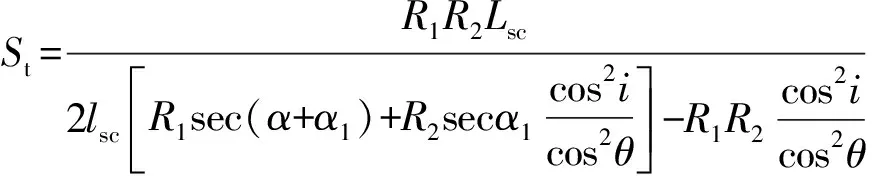
(7)
由式(6)和式(7)可以看出,變量α和α1均影響弧矢像距Ss和子午像距St的大小。所以這里分別討論了α和α1影響像散S=Ss-St的校正情況。
在同一光學(xué)系統(tǒng)下,當(dāng)R1,R2,Lsc,i,θ,α1為定值時(shí),僅存在變量α影響Ss和St。顯然,cos(α+α1)越小,則Ss越小;α越大,sec(α+α1)越大,則St越大,故而Ss與St的差值減小,光學(xué)系統(tǒng)的像散校正能力增強(qiáng);當(dāng)R1,R2,Lsc,i,θ,α為定值時(shí),僅存在變量α1影響Ss和St。同理,α1越大,cos(α+α1)越小,Ss越小,sec(α+α1)越大,St越大,故而Ss與St的差值減小,光學(xué)系統(tǒng)的像散校正能力增強(qiáng)。
可見,同一光學(xué)系統(tǒng)下,通過改變?chǔ)梁挺?調(diào)整C-T結(jié)構(gòu)的像散校正情況,可為后續(xù)的寬波段消像散型光譜儀設(shè)計(jì)提供理論依據(jù)。
3 像散校正分析
3.1平面光柵置于發(fā)散光路
平面光柵置于發(fā)散光路中,光束經(jīng)過3次離軸反射式元件依次成像,生成相應(yīng)的離散子午像距和弧矢像距。令Ss=St,可以推導(dǎo)出中心波長的零階消像散條件[12]。
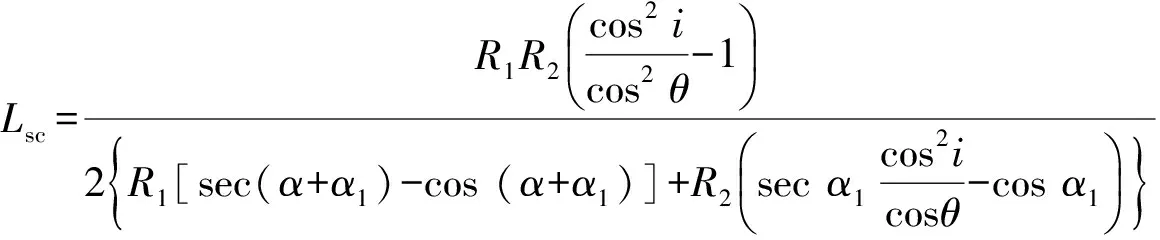
(8)
通過式(8)可以有效消除C-T結(jié)構(gòu)中心波長處的像散。隨后,D.R.Austin等[11]給出了子午像距Ss和弧矢像距St隨衍射角θ的變化關(guān)系,即一階消像散條件,通過此關(guān)系可以消除臨近中心波長一定范圍的像散。因此,在設(shè)計(jì)寬波段C-T結(jié)構(gòu)時(shí),需要了解一階消像散條件對邊緣波段的約束能力,從而進(jìn)一步校正光學(xué)系統(tǒng)的像散。
3.2邊緣波段像散校正
聯(lián)立式(4)和式(5)得到光學(xué)系統(tǒng)的像散如下:
S(λ)=Ss-St=
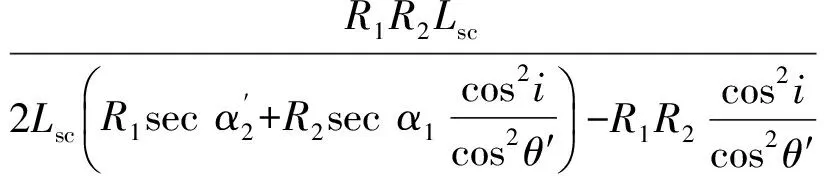
(9)
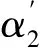
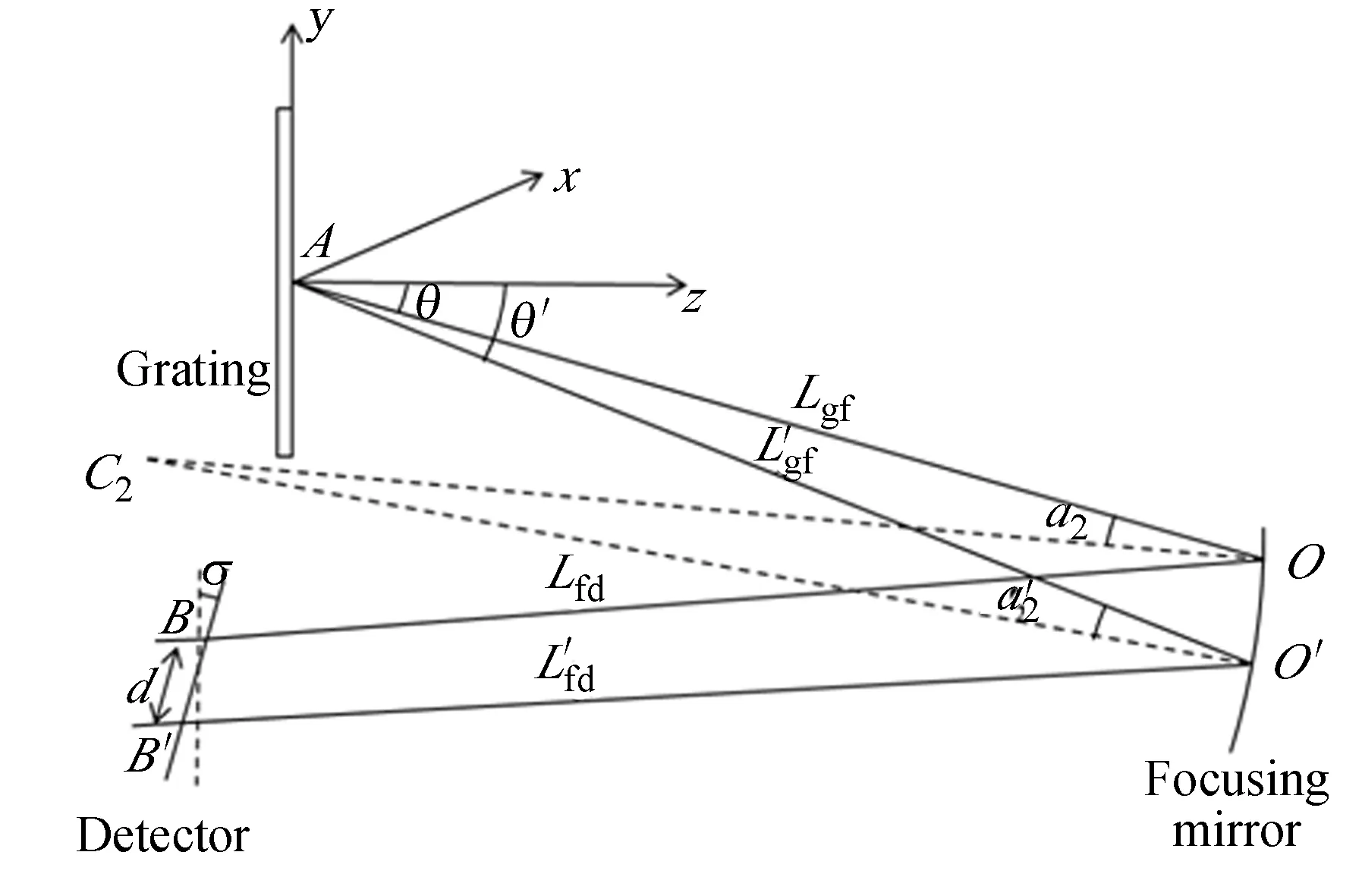
圖3 平面光柵與聚焦鏡的幾何關(guān)系圖Fig.3 Geometric relations between plane grating and condensing mirror
根據(jù)圖3所示的坐標(biāo)系,相應(yīng)的矢量坐標(biāo)如下:
AO=(Lgfsinθ,Lgfcosθ),
(10)
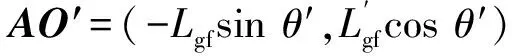
(11)
C2O=(-R2sin (θ-α2),R2cos(θ-α2)),
(12)
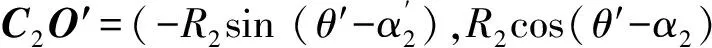
(13)
由矢量和AO+OC2+C2O′+O′A建立平面光柵與聚焦鏡的幾何關(guān)系,聯(lián)立式(10)~式(13)得到:
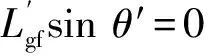
(14)
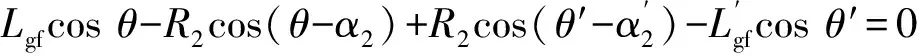
(15)
聯(lián)立式(14)和式(15)可得:
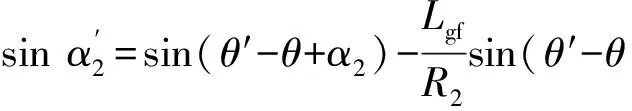
(16)
圖4模擬了C-T結(jié)構(gòu)全波段像散隨波長變化的曲線,可表征光學(xué)系統(tǒng)的像散校正能力。模擬過程中,考慮離軸角對C-T結(jié)構(gòu)成像質(zhì)量的影響,設(shè)定準(zhǔn)直鏡離軸角α1為5°~8°,其余的結(jié)構(gòu)參數(shù)相同。圖4(a)、4(b)、4(c)、4(d)分別模擬了α取1°,2°,3°,4°,光譜覆蓋900~1 700 nm時(shí)的像散校正情況。通過觀察不同變化關(guān)系曲線,可以明顯看出α對像散校正能力的影響。
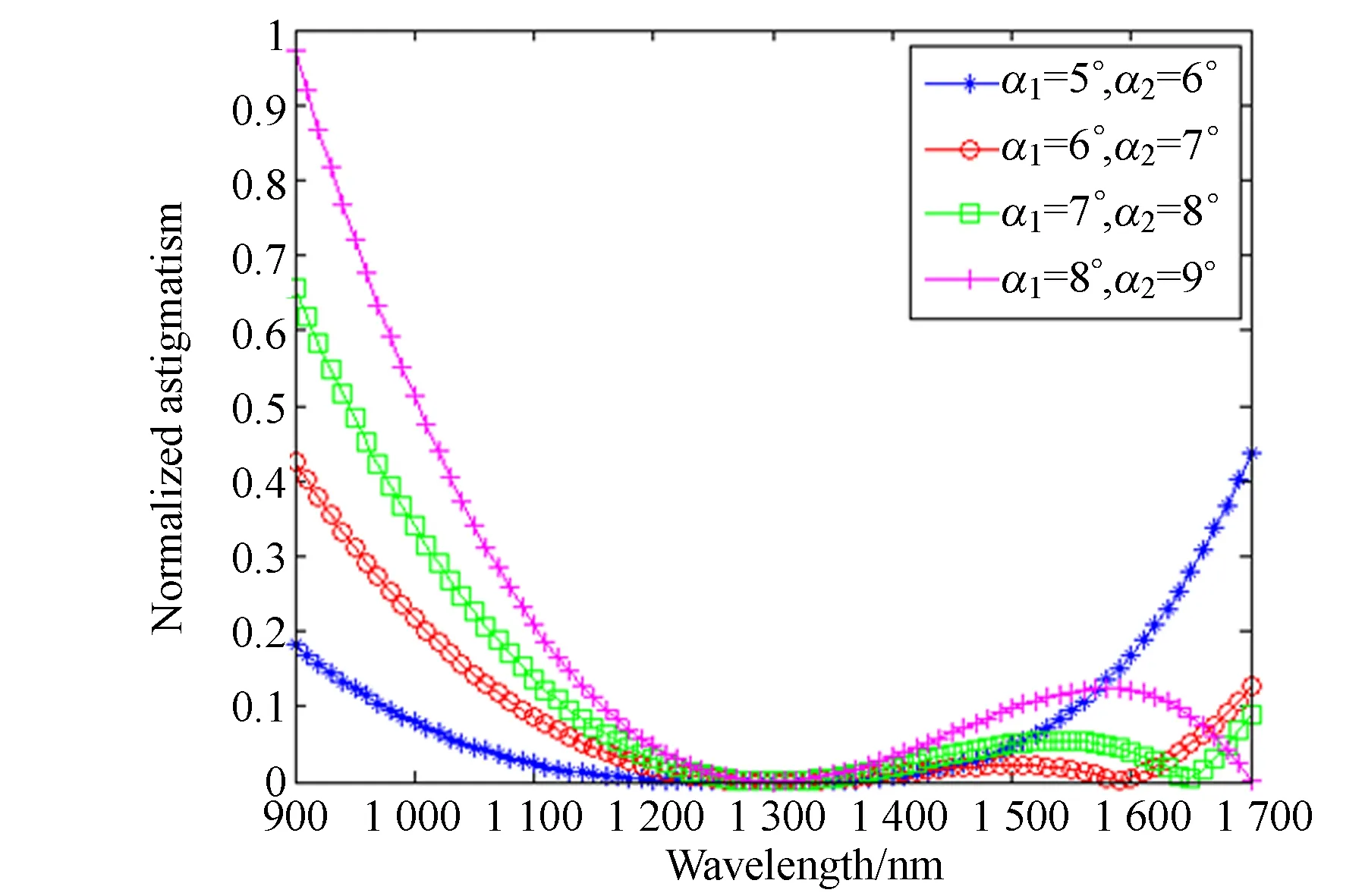
(a)α=1°
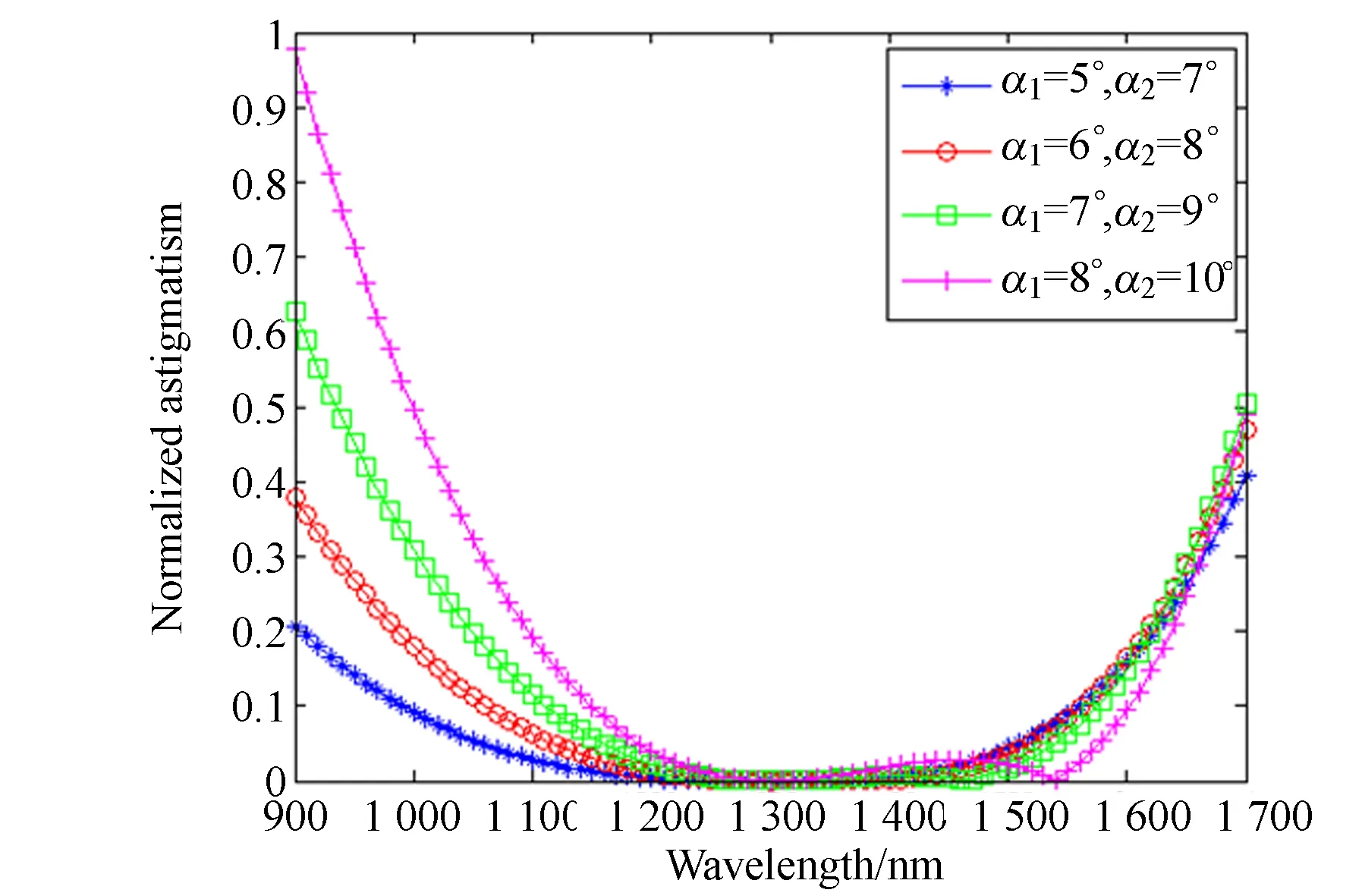
(b) α=2°
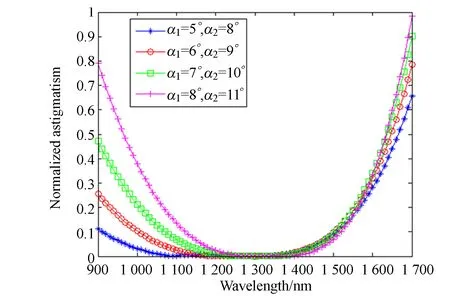
(c) α=3°
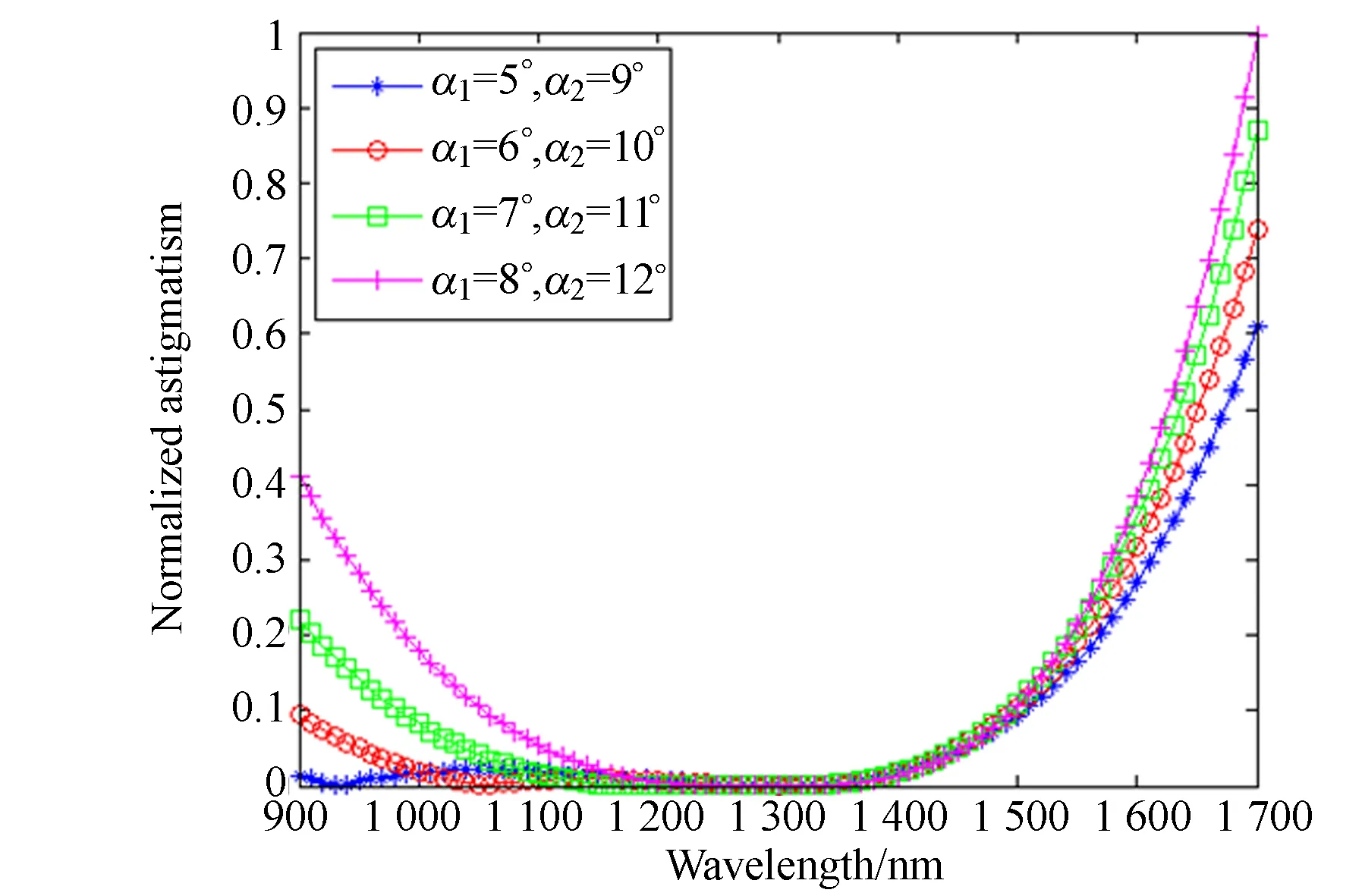
(d) α=4°圖4 900~1 700 nm全波段像散隨波長變化的曲線Fig.4 Astigmatism versus wavelength over full spectral range of 900~1 700 nm
較小邊緣波長到中心波長的波段定義為短波波段(900~1 300 nm),中心波長到較大邊緣波長的波段定義為長波波段(1 300~1 700 nm)。對比圖4(a)~4(d)可知,當(dāng)準(zhǔn)直鏡離軸角α1相同時(shí),隨著α的增大,短波波段的像散校正能力越來越強(qiáng),長波波段的校正能力越來越弱; 當(dāng)α相同時(shí),隨著準(zhǔn)直鏡離軸角α1和聚焦鏡離軸角α2的同時(shí)增大,邊緣波段的像散校正能力明顯減弱,不過全波段像散的變化趨勢相似,離軸角的增大對短波波段像散校正能力的影響較大。
4 實(shí)驗(yàn)及結(jié)果分析
4.1設(shè)計(jì)實(shí)例
為了驗(yàn)證準(zhǔn)直鏡離軸角與聚焦鏡離軸角的角度差值α對C-T結(jié)構(gòu)邊緣波段像散校正能力的影響,分別設(shè)計(jì)了相同結(jié)構(gòu)參數(shù)下,α取不同值時(shí)的寬波段C-T結(jié)構(gòu)光學(xué)系統(tǒng),初始結(jié)構(gòu)的基本參數(shù)如表1所示。

表1 寬波段Czerny-Turner結(jié)構(gòu)基本參數(shù)
對比圖4的模擬結(jié)果可知,當(dāng)準(zhǔn)直鏡離軸角α1=6°時(shí),短波波段和長波波段的像散校正情況合理,因此,這里取α1=6°進(jìn)行實(shí)驗(yàn)仿真和分析。根據(jù)初始的基本參數(shù),用Matlab計(jì)算出C-T結(jié)構(gòu)的其余參數(shù),將其結(jié)果依次導(dǎo)入光學(xué)設(shè)計(jì)軟件Zemax中進(jìn)行光線追跡和設(shè)計(jì)優(yōu)化,初始參數(shù)和優(yōu)化參數(shù)如表2所示。
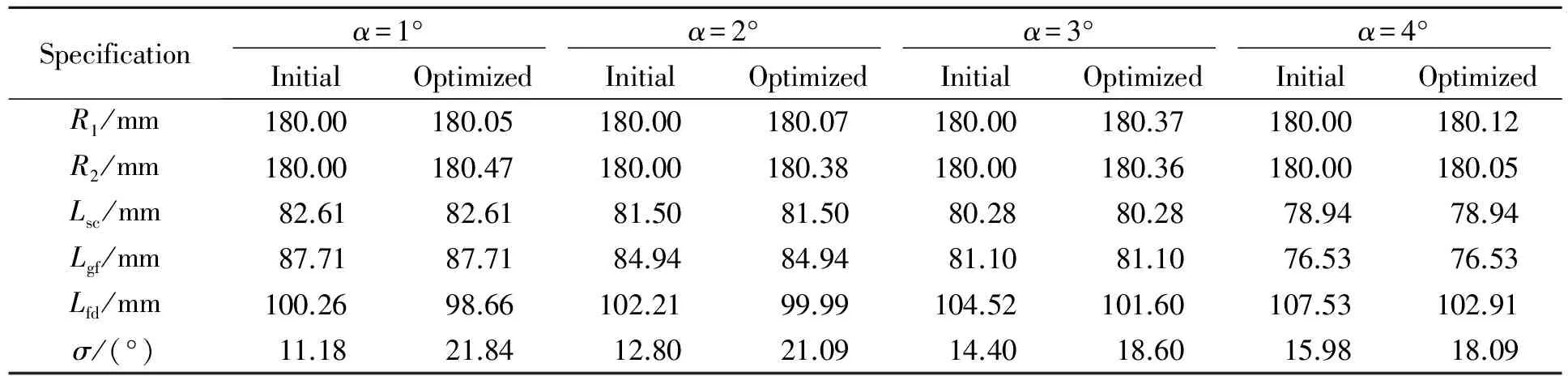
表2 寬波段Czerny-Turner結(jié)構(gòu)的設(shè)計(jì)參數(shù)
4.2結(jié)果分析
圖5給出了α分別取1°,2°,3°和4°時(shí),C-T結(jié)構(gòu)在全波段全視場的RMS值隨波長的變化曲線。對比圖4(a)~4(d)可知,一階消像散條件的像散校正能力有限,隨著光譜范圍的加寬,對邊緣像散的約束能力越來越弱;隨著聚焦鏡離軸角與準(zhǔn)直鏡離軸角的角度差值α增大,短波波段的像散校正能力增強(qiáng),長波波段的像散校正能力減弱。

(a) α=1°

(b) α=2°
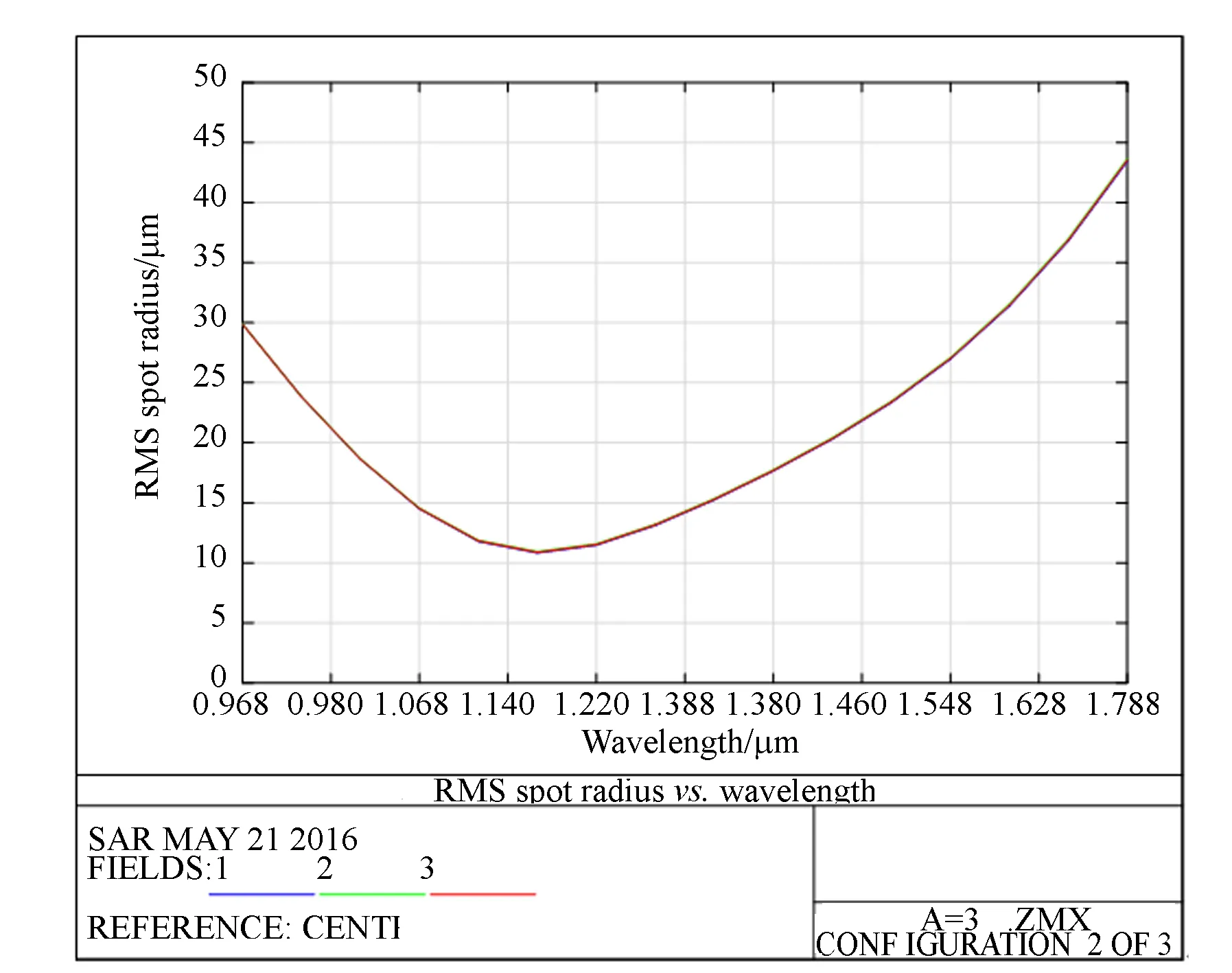
(c) α=3°
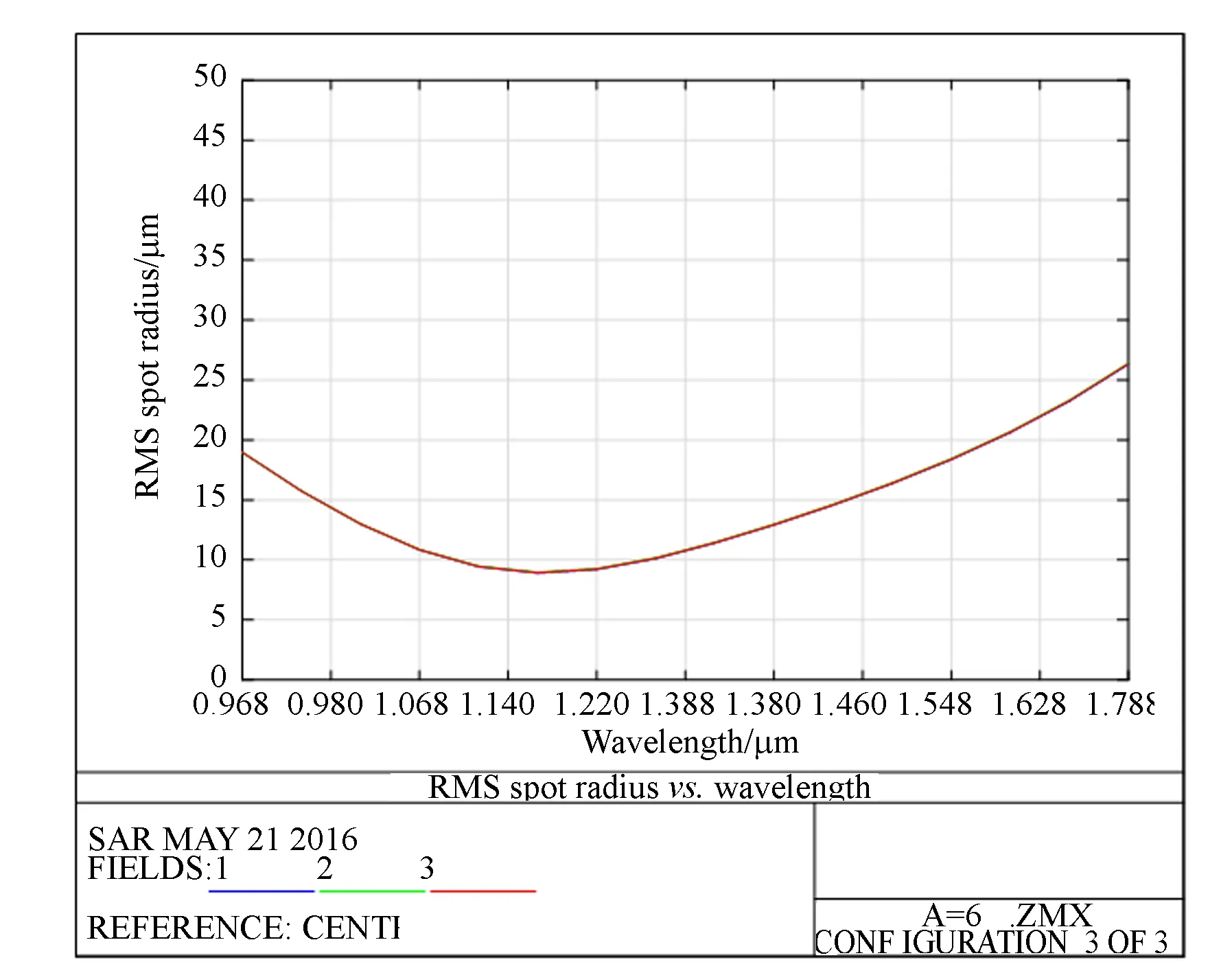
(d) α=4°圖5 全波段全視場的點(diǎn)列圖Fig.5 RMS spot radii at all wavelengths in full fields of view
由圖5可以看出,中心波長處的RMS值不為零,設(shè)計(jì)結(jié)果依然存在一定的彌散斑,主要體現(xiàn)為由球差像差。由于彗差的存在,導(dǎo)致短波波段(900~1 300 nm)與長波波段(1 300~1 700 nm)的彌散斑尺寸不一致。若忽略球差和彗差對光學(xué)系統(tǒng)的影響,設(shè)計(jì)優(yōu)化結(jié)果與理論模擬分析結(jié)果的變化趨勢基本一致。
為了更全面地說明α值對邊緣波段像散校正能力的影響,表3給出了中心視場處中心波長和邊緣波長的RMS值。
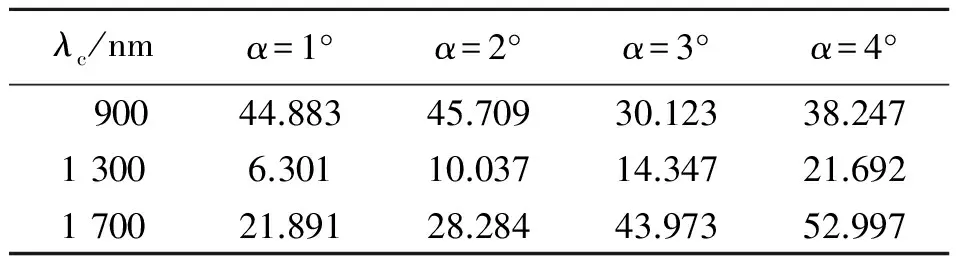
表3 中心視場處RMS值
為了橫向比較不同角度偏差下的像散校正能力,將邊緣波長與中心波長的RMS差值進(jìn)行數(shù)據(jù)處理,即RMSabsolute(α)=RMSe(α)-RMSc(α),采用相鄰α差值的RMSabsolute(α)比值進(jìn)行比較分析。圖6給出了RMSabsolute(α)與波長的關(guān)系曲線。
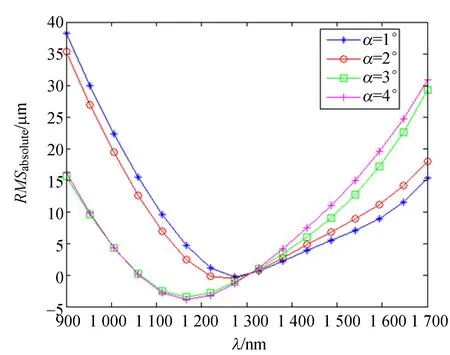
圖6 RMSabsolute(α)隨波長的變化曲線Fig.6 RMSabsolute(α) versus wavelength in whole band
在比較分析過程中,定義相鄰α值下的RMSabsolute比值為δ,作為評(píng)價(jià)像散校正能力的標(biāo)準(zhǔn),具體公式如下:

(17)
根據(jù)式(17)可以計(jì)算出不同情況下的δ值,比較δ1,δ2,δ3,短波波段的像散校正能力越來越強(qiáng),像散校正能力平均提高了1.6倍左右;長波波段的像散校正能力越來越弱,像散校正能力平均提高了0.79倍左右,即降低了1.27倍左右。
5 結(jié) 論
本文基于發(fā)散光束照射平面光柵的像差理論,研究了寬光譜范圍下影響像散校正能力的因素,并分析了準(zhǔn)直鏡離軸角與聚焦鏡離軸角的角度差值α和光學(xué)系統(tǒng)像散S之間的關(guān)系。理論模擬和設(shè)計(jì)仿真了相同結(jié)構(gòu)參數(shù)下,光譜覆蓋900~1 700 nm的C-T結(jié)構(gòu)的像散校正情況。實(shí)驗(yàn)結(jié)果表明,一階消像散條件對寬波段C-T結(jié)構(gòu)的像散校正能力有限,離軸角增大導(dǎo)致全波段校正能力減弱,邊緣波段的像散擴(kuò)大明顯;準(zhǔn)直鏡離軸角與聚焦鏡離軸角的角度差值α不同時(shí),對邊緣波段像散的約束能力不同,且隨著α逐漸增大。短波波段的校正能力平均提高了1.6倍左右,長波波段的校正能力平均降低了1.27倍左右。這些結(jié)論為寬波段光譜儀的像散校正提供了有價(jià)值的參考。
[1]陳偉,鄭玉全,薛慶生. 機(jī)載寬視場大相對孔徑成像光譜儀[J]. 光學(xué) 精密工程,2015,23(1):15-21.
CHEN W, ZHENG Y Q, XUE Q SH. Airborne imaging spectrometer with wide field of view and large relative-aperture[J].Opt.PrecisionEng.,2015,23(1):15-21. (in Chinese)
[2]張晶,王淑榮,黃煜,等. 臨邊成像光譜儀的發(fā)展現(xiàn)狀與進(jìn)展[J]. 中國光學(xué),2013,6(5):692-700.
ZHANG J, WANG SH R, HUANG Y,etal.. Status and development of limb imaging spectrometer[J].ChineseOptics,2013,6(5):692-700. (in Chinese)
[3]崔繼承,唐國玉,撖芃芃,等. 用于腫瘤手術(shù)在線診斷的成像光譜儀的研制[J]. 光學(xué) 精密工程,2013,21(12):3043-3049.
CUI J CH, TANG Y G, HAN P P,etal.. Development of diagnostic imaging spectrometer for tumor on-line operation[J].Opt.PrecisionEng.,2013,21(12):3043-3049. (in Chinese)
[4]曹海霞,吳娜,馮樹龍,等. 單色儀與成像光譜儀的交互光譜定標(biāo)[J]. 光學(xué) 精密工程,2014,22(10):2586-2591.
CAO H X, WU N, FENG SH L,etal.. Cross-spectral calibration for monochromator and imaging spectrometer[J].Opt.PrecisionEng.,2014,22(10):2586-2591. (in Chinese)
[5]MASAYUKI F,TAKEHIKO TAKENOUCHI,KEI-ICHI K. Highly efficient and aberration-corrected spectrometer for advanced Raman spectroscope[J].AppliedOptics,2002,41(22):4655-4665.
[6]XU L,CHEN K X, HE Q SH,etal.. Design of freeform mirrors in Czerny-Turner spectrometers to suppress astigmatism[J].AppliedOptics,2009,48(15):2871-2879.
[7]SUNG K, THOMPSON K P,ROLLAND J. Broadband antigmatism-corrected Czerny-Turner spectrometer[J].OpticsExperess,2010,18(22):23378-23384.
[8]QU B X, GUO X,YU F H. Optimization of freeform cylindrical lens in Czerny-Turner spectrometer system to correct the astigmastism by using user defined error function[J].SPIE,2012,8416:84161I.
[9]XUE Q SH. Astigmastism-corrected Czerny-Turner imaging spectrometer for broadband spectral simultaneity[J].AppliedOptics,2011,50(10):1338-1344.
[10]唐義,張止戈,陳延愛,等. 一種基于柱面反射鏡的紫外/可見光成像光譜儀[J]. 光學(xué)學(xué)報(bào),2013,33(3):0330004.
TANG Y, ZHANG ZH G, CHEN Y A,etal.. Designed of visible-ultraviolet cylinder mirror imaging spectrometer[J].ActaOpticaSinica, 2013,33(3):0330004. (in Chinese)
[11]AUSTIN D R,WITTING T,WALMSLEY I A. Broadband astigmatism-free Czerny-Turner imaging spectrometer using spherical mirrors[J].AppliedOptics,2009,48(19):3846-3853.
[12]BATE B,DOWELL M,NEWTON A C. Correction of astigmatism in a Czerny-Turner spectrograph using a plane grating in divergent illumination[J].J.Phys.,1970,E3(3):206-210.

董科研(1980-),男,吉林長春人,博士,副教授,主要從事激光通信及光學(xué)系統(tǒng)設(shè)計(jì)方面的研究。E-mail: dongkeyan@163.com

李欣航(1991-),女,吉林長春人,碩士研究生,2010年于長春理工大學(xué)獲得學(xué)士學(xué)位,主要從事光學(xué)系統(tǒng)設(shè)計(jì)方面的研究。Email: 317554403@qq.com
(版權(quán)所有未經(jīng)許可不得轉(zhuǎn)載)
Influence factors of Czerny-Turner edge band astigmatism correction
DONG Ke-yan1, LI Xin-hang1,2*, AN Yan1
(1.Institute of Space Photoelectric Technology, ChangchunUniversityofScienceandTechnology,Changchun130022,China;2.Opto-electronicsEngineerInstitute,ChangchunUniversityofScienceandTechnology,Changchun130022,China)*Correspondingauthor,E-mail: 317554403@qq.com
To improve the weak correcting capacity of a wide band Czerny-Turner structure, the influence factors on the astigmatism correction of an optical system were analyzed. The Matlab software was used to simulate and analyze the reasons that the astigmatism was produced and the traditional method could not suppress the astigmatism. Then, the dependence of the angle differenceαbetween the off-axis angle of collimator mirror and the off-axis angle of focusing mirror on the astigmatismSof the optical system was discussed. The astigmatism correction of wide band Czerny-Turner structure was simulated at differentαvalues. To verify the validity of the theoretical analysis, an astigmatic Czerny-Turner system ranging from 900 to 1 700 nm was designed, the Zemax was used to perform the ray tracing and optimal design and the design results were processed and analyzed. The simulation results demonstrate that the shortwave band astigmatism correction ability is getting stronger with increasing the difference angle, which may achieve about 1.6 times on increase. However, long wave band astigmatism correction ability is more and more weak, which may reduce about 1.27 times on average. It suggests that the reasonable selection of the difference angle can provide the theoretical guidance for correcting the astigmatism of wide band Czerny-Turner structures.
optical design; Czerny-Turner structure; astigmatism correction; edge band
2016-05-31;
2016-06-30.
長春市科技局科技支撐計(jì)劃資助項(xiàng)目(No.14DR003);校內(nèi)青年科學(xué)基金資助項(xiàng)目(No.XQNJJ-2013-12);吉林省教育廳“十三五”科學(xué)技術(shù)研究項(xiàng)目(吉教科合字[2016]第368號(hào))
1004-924X(2016)10-2384-08
O435.1;TH703
Adoi:10.3788/OPE.20162410.2384

