基于AHP-TOPSIS模型的巖土邊坡穩(wěn)定性評價

姜廷文，靳春玲

（蘭州交通大學土木工程學院，甘肅 蘭州 730070）

基于AHP-TOPSIS模型的巖土邊坡穩(wěn)定性評價

姜廷文，靳春玲

（蘭州交通大學土木工程學院，甘肅 蘭州 730070）

選用巖石質量指標、巖體完整性指標、地應力、黏聚力、內摩擦角、坡高和日最大降水量7個影響因素作為邊坡穩(wěn)定性評價指標，采用改進的層次分析法（AH P）計算各評價指標的權向量，結合逼近理想解排序法 （TOPSIS）構建改進的AH P-TOPSIS模型。依據單指標等級分類區(qū)間的下限構造5個不同等級的臨界值邊坡，將其穩(wěn)定性指標臨界值與4組邊坡穩(wěn)定性指標實測數據一同代入AH P-TOPSIS評判模型，通過計算它們與理想解的貼進度來劃分穩(wěn)定性等級分類區(qū)間，進而與4組待評價邊坡貼進度對比確定出邊坡穩(wěn)定性等級。研究結果表明，采用AH P-TOPSIS模型對邊坡穩(wěn)定性的評價結果與灰色關聯(lián)法和可拓評價法等結果基本相符，證明該模型的可行性，為邊坡穩(wěn)定性評價提供了一種新的分析方法。

邊坡；穩(wěn)定性評價；改進的AH P；AH P-TOPSIS模型

0　引言

在鐵路、公路、水利、建筑及礦山等工程項目中，巖土邊坡的穩(wěn)定性對工程選址、工程質量、工程耐久性及工程安全性有直接和間接的影響［1］，合理地評價邊坡穩(wěn)定性對工程項目具有重要意義。由于邊坡穩(wěn)定性影響因素的復雜性和不確定性，傳統(tǒng)的單指標或少數指標評價方法會遺漏重要信息，不能夠全面準確地評價邊坡的穩(wěn)定［2，3］。為了適應邊坡穩(wěn)定性影響因素的特征，大量文獻已提出了不確定性指標的評價模型，如模糊數學方法［4，5］、灰關聯(lián)分析方法［6］、因子分析法［7］、人工神經網絡法［8，9］及可拓評價法［10，11］等。這些方法都有各自的側重點和優(yōu)勢，但也存在一定的缺陷。例如，傳統(tǒng)的模糊分析方法計算復雜，對指標權重矢量的確定主觀性較大；人工神經網絡法雖克服了權重確定的主觀性，但應用中需要大量的實際學習樣本，而樣本獲取較為困難；因子分析法把多個指標中的大部分信息濃縮到少數幾個指標中，使?jié)饪s后因子的意義不能完全確定，而且會有一些信息未被提取。

為此，結合巖土邊坡穩(wěn)定性影響因素的特點，本文采用改進的3標度層次分析法（anal yt i c hi erarchy process，AH P）和逼近理想解排序法［12］（TOPSIS）相結合應用于穩(wěn)定性評價中。考慮到傳統(tǒng)的9標度層次分析法中對判斷矩陣一致性檢驗的問題，采用3標度層次分析法降低權重確定的主觀性，避免了一致性檢驗，減少計算量，提高了計算精度，并且把多目標決策理論中的TOPSIS引入巖土邊坡穩(wěn)定性評價中，構成AH P-TOPSIS綜合評價模型，為巖土邊坡穩(wěn)定性評價提供了一種新思路。

1　改進的AH P法及權重確定步驟

1.1改進的AHP法

層次分析法（AH P）是將決策總是有關的元素分解成目標、準則、方案等層次，在此基礎之上進行定性和定量分析的決策方法。該方法是美國運籌學家匹茨堡大學教授薩蒂于20世紀70年代初提出的一種層次權重決策分析方法。改進的3標度AH P法是將同一層的指標兩兩比較，改變傳統(tǒng)9標度法中9種判斷原則，通過3種判斷原則確定其相對重要性，從而減小和避免多原則判斷主觀性造成的誤差［13］。

1.2權重確定的步驟

1.2.1構造比較矩陣

假定指標集Z=｛z1，z2，…，zn｝，其中，zi為第i個評價指標（i=1，2，…，n），n為評價指標總數。用3標度原則對評價指標兩兩對比，構造的比較矩陣為

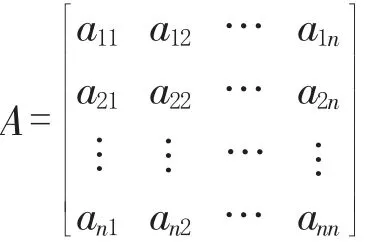
其中3標度矩陣含義見表1。

表1　3標度矩陣含義

1.2.2將比較矩陣A轉化為最優(yōu)傳遞矩陣

最優(yōu)傳遞矩陣為

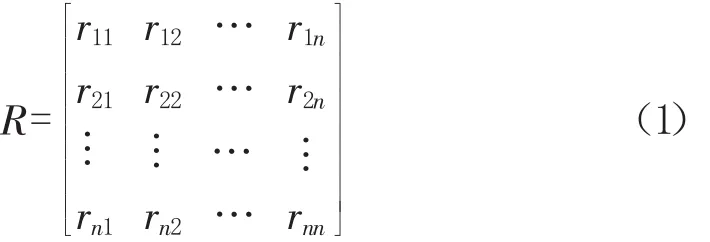
1.2.3把最優(yōu)傳遞矩陣R轉化為一致判斷矩陣

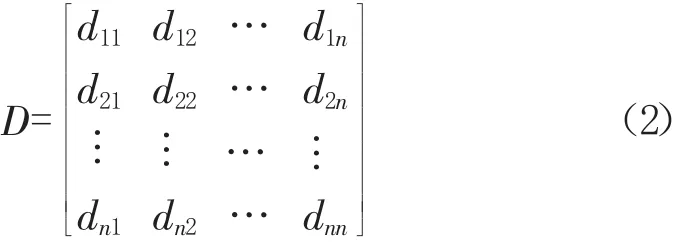
1.2.4評價指標權重計算

通過計算一致判斷矩陣D的最大特征值及對應特征向量確定權重，即滿足式DW=λmaxW的特征向量作為評價指標的權重，其中特征值向量采用方根法求解。

權重向量W=［w1w2… wn］計算公式為

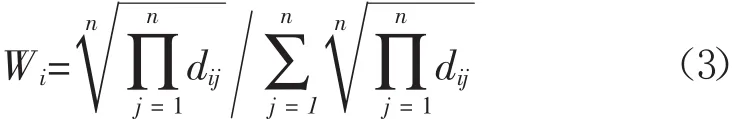
2　AH P-TO PSI S評判模型的建立

在多目標決策分析中，逼近理想解排序法（TOPSIS）是一種常用的有效評價方法，又稱優(yōu)劣解距離法、理想解法、理想點法。TOPSIS法是通過有限個評價對象正負理想解的貼進度進行排序的方法［14，15］。

2.1構造初始判斷矩陣

設評價對象集P=｛P1，P2，…，Pm｝，每個評價對象有n個評價指標X=｛X1，X2，…，Xn｝，相應的評價指標Xij表示第m個評價單元的第n個評價指標。其中，i=（1，2，…，m），j=（1，2，…，n），則構造的初始判斷矩陣為

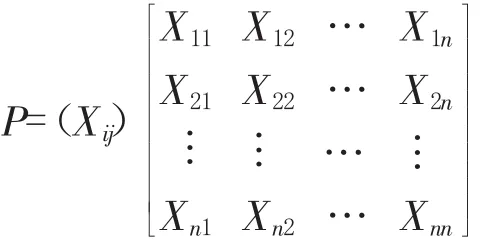
2.2建立規(guī)范化決策矩陣

考慮到評判對象中不同的評判指標具有不同的量綱和單位，為了消除由此產生的指標的不可公度性，對評判指標進行無量綱化處理（同趨勢化）［12，14，15］，得到規(guī)范化決策矩陣B。其中，B=（bij）m×n的元素計算如下：

收益性指標，越大越優(yōu)，即

2.3建立加權規(guī)范化決策矩陣

加權規(guī)范化決策矩陣通過規(guī)范化決策矩陣B的每列與改進的層次分析法所確定的權重wj相乘得到，即

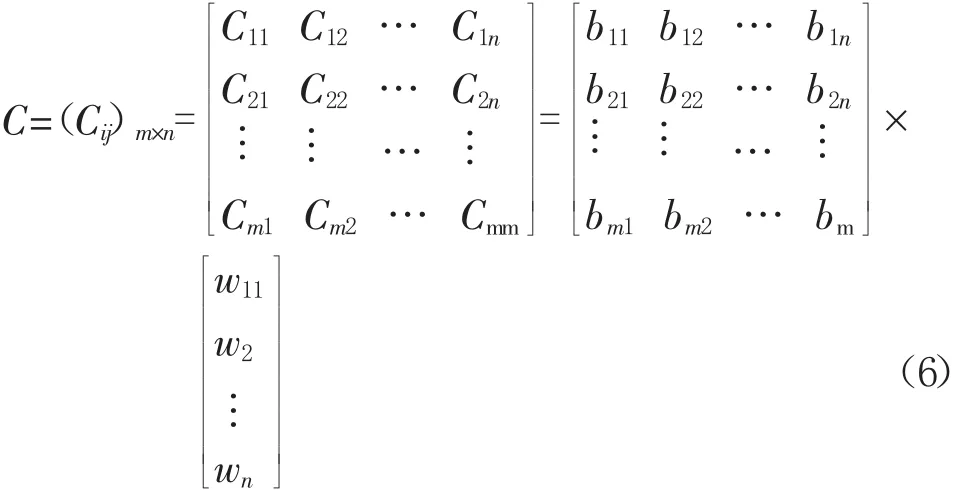
2.4評價對象貼近度分析

2.4.1確定加權規(guī)范化決策矩陣C的正理想解C+和負理想解C

C+=｛maxci1，maxci2，…，maxcin｝=｛c1+，c2+，…，cn+｝

（其中，如果指標沒有同趨勢化，收益性指標取最大值，消耗性指標取最小值）

C-=｛minci1，minci2，…，mincin｝=｛c1-，c2-，…，cn-｝

（其中，如果指標沒有同趨勢化，收益性指標取最小值，消耗性指標取最大值）

2.4.2計算各評價對象與理想解的距離

評價對象到正理想解的距離

2.4.3計算各評價對象與正理想解的貼進度

貼近度fi+反映了評判對象靠近正理想解、遠離負理想解的程度，fi+越大，評判對象越靠近正理想解。當評判對象為正理想解時，fi+=1；當評判對象為負理想解時，fi+=0。但一般評判對象貼近度都在0～1，故只考慮評判對象靠近正理想解的貼近度，通過貼近度值降序排列，可以對評判對象進行選擇評判。

3　邊坡穩(wěn)定性評價實例應用

3.1邊坡穩(wěn)定性影響因素

影響邊坡穩(wěn)定性的指標很多，參考有關巖土邊坡穩(wěn)定性評價體系［10，11］，考慮主要影響因素，經綜合分析后確定以巖石質量指標（X1）、巖體完整性指標（X2）、地應力（X3）、黏聚力（X4）、內摩擦角（X5）、坡高（X6）和日最大降水量（X7）7個指標作為影響邊坡穩(wěn)定性的因素。它們基本反映了地層巖性、地質構造、巖體結構、水文地質條件、地應力分布等性質，且這些指標比較容易獲得。

3.2邊坡穩(wěn)定性等級分類標準

按照邊坡穩(wěn)定性影響因素的單指標分類區(qū)間將邊坡穩(wěn)定性程度劃分為5個等級，分別為穩(wěn)定Ⅰ級、較穩(wěn)定Ⅱ級、基本穩(wěn)定Ⅲ級、不穩(wěn)定Ⅳ級和極不穩(wěn)定Ⅴ級［6，10，11］。穩(wěn)定性等級評價準則見表2。

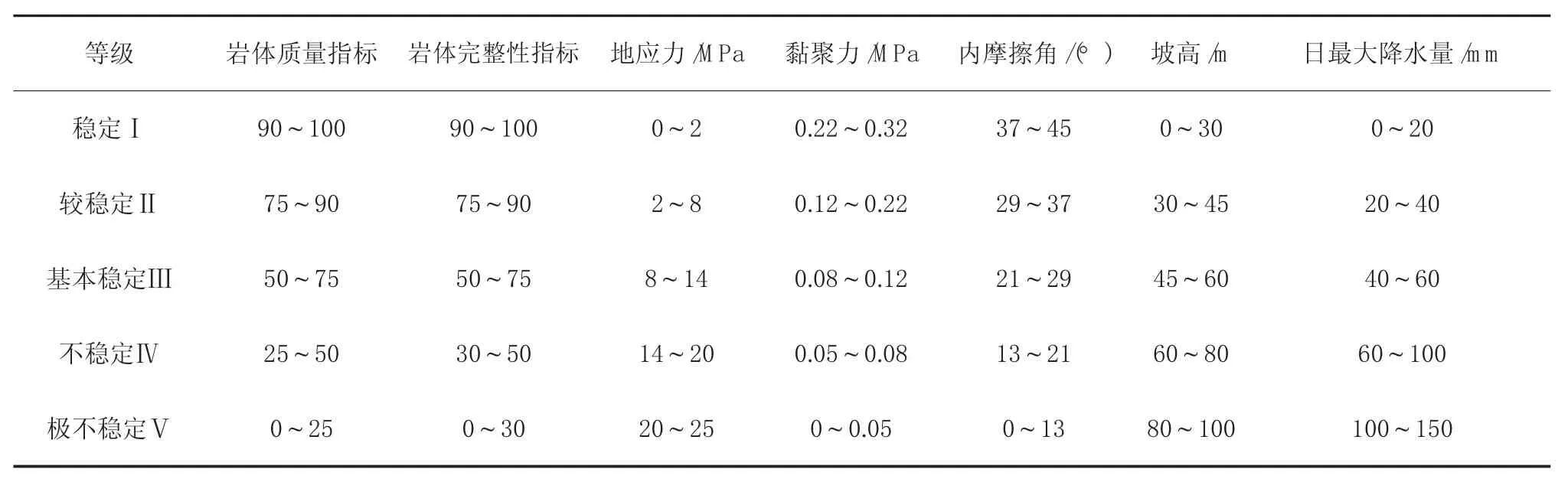
表2　邊坡穩(wěn)定性分類準側

3.3邊坡穩(wěn)定性評價指標權重確定

根據改進層次分析法的基本原理，查閱大量文獻及工程資料，并與現場工作者、有關專家學者協(xié)商，構造的比較矩陣為

將比較矩陣A用式（1）轉化為最優(yōu)傳遞矩陣R，有

由式（2）將矩陣R轉化為一致性判斷矩陣D，有

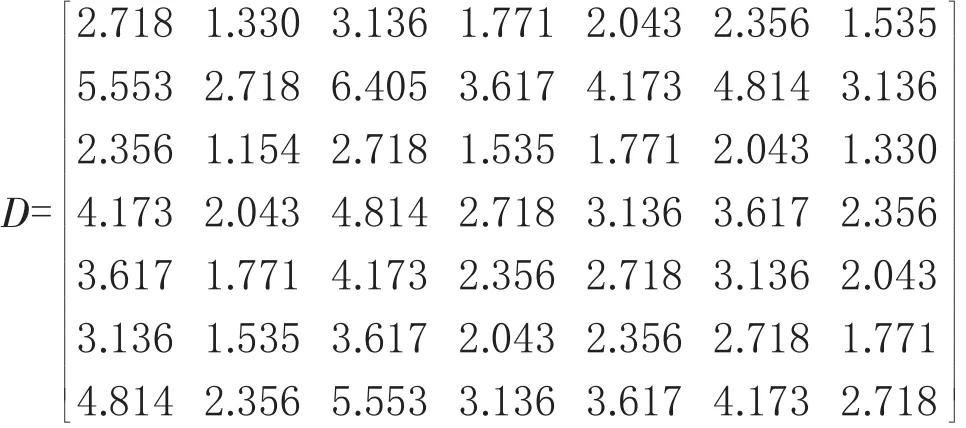
由式（3）計算各評價指標權重為

w1=0.262 4，w2=0.536 1，w3=0.227 5，w4=0.402 9，w5=0.349 3，w6=0.308 2，w7=0.464 7

分析可知，巖體完整性指標對邊坡穩(wěn)定性影響最大，其次是日最大降水量、黏聚力、內摩擦角、坡高及巖石質量指標，影響最小的是地應力。

3.4AHP-TOPSISI模型及實例應用

將改進的AH P-TOPSIS模型應用于文獻［16］中公路邊坡（S1）和文獻［11］中礦區(qū)邊坡（S2，S3，S4）穩(wěn)定性評價。其中，S1、S2、S3、S4邊坡穩(wěn)定性指標的實測數據見表3。

根據表2中單指標分類區(qū)間下限構造的5個不同等級的臨界值邊坡Ⅰ0、Ⅱ0、Ⅲ0、Ⅳ0、Ⅴ0，與表3穩(wěn)定性待評價邊坡S1、S2、S3、S4的實測數據構造AH P-TOPSISI模型的初始評判矩陣P，其中前5行為臨界值邊坡數據，后4行為待預測邊坡的評價指標數據。

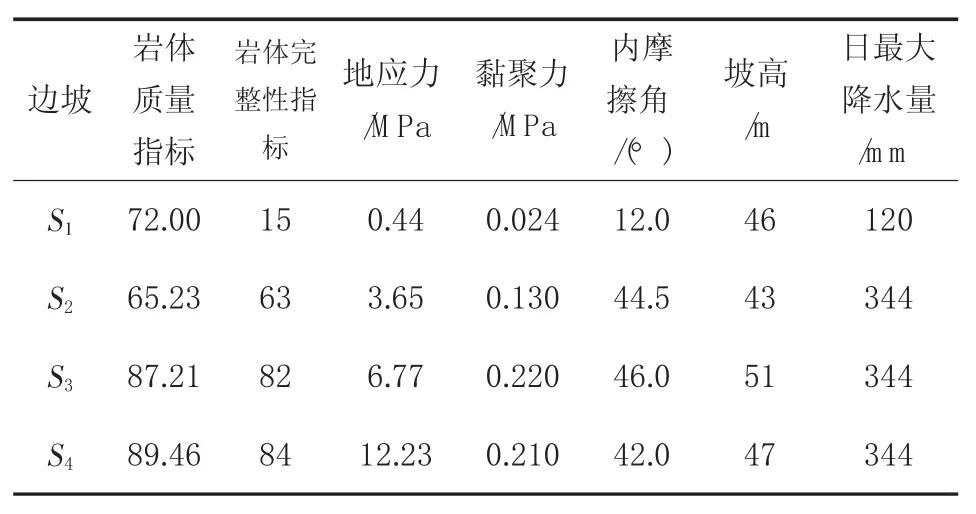
表3　穩(wěn)定性指標實測數據

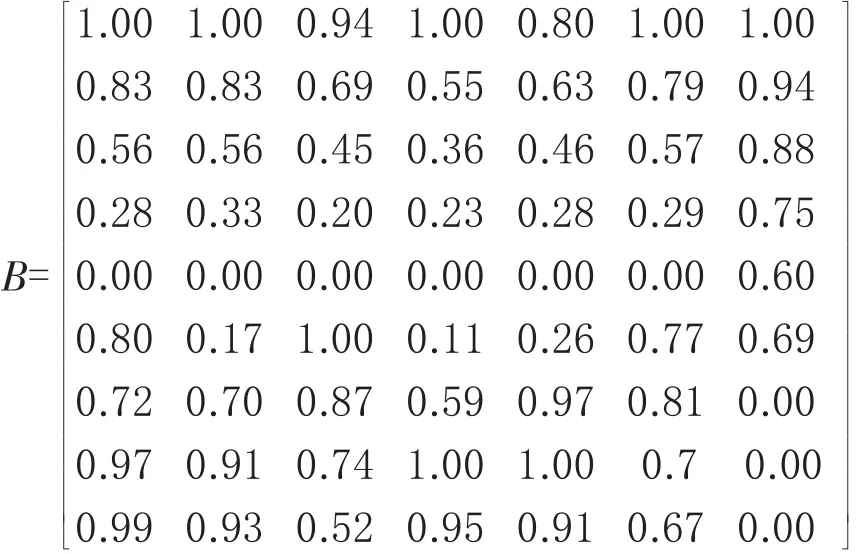
對初始判斷指標進行無量綱化處理，由表2可知指標X1、X2、X4、X5為收益性指標，越大越好，由式（4）處理；指標X3、X6、X7為消耗性指標，越小越好，由式（5）處理；得到規(guī)范化決策矩陣B。

由式（6），計算得到加權規(guī)范化決策矩陣C。

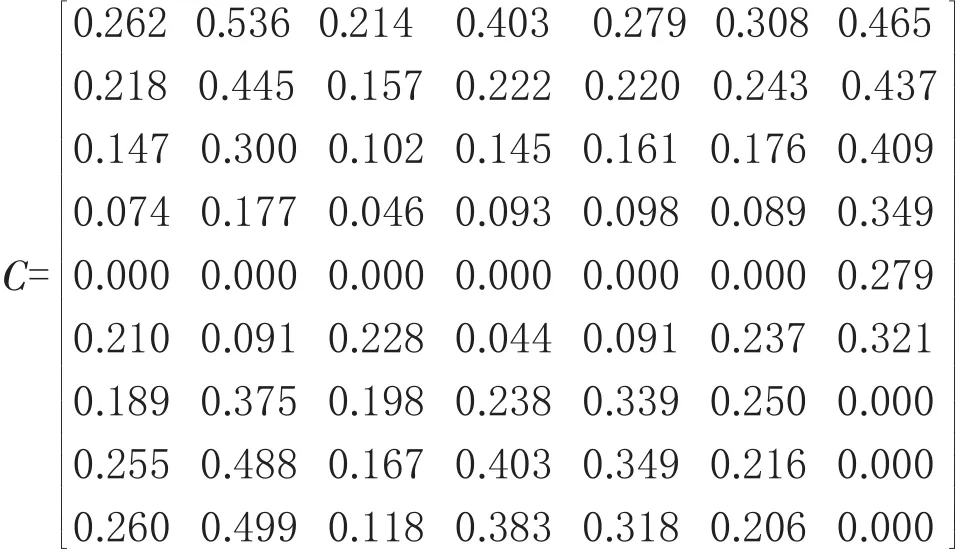
由加權規(guī)范化矩陣C可得正理想解與負理想解

由式（7）～式（9）可得到臨界值邊坡穩(wěn)定性及待評價邊坡穩(wěn)定性距正理想解的距離Di+，距負理想解的距離Di-，以及與正理想解的貼近度fi+，結果見表4。

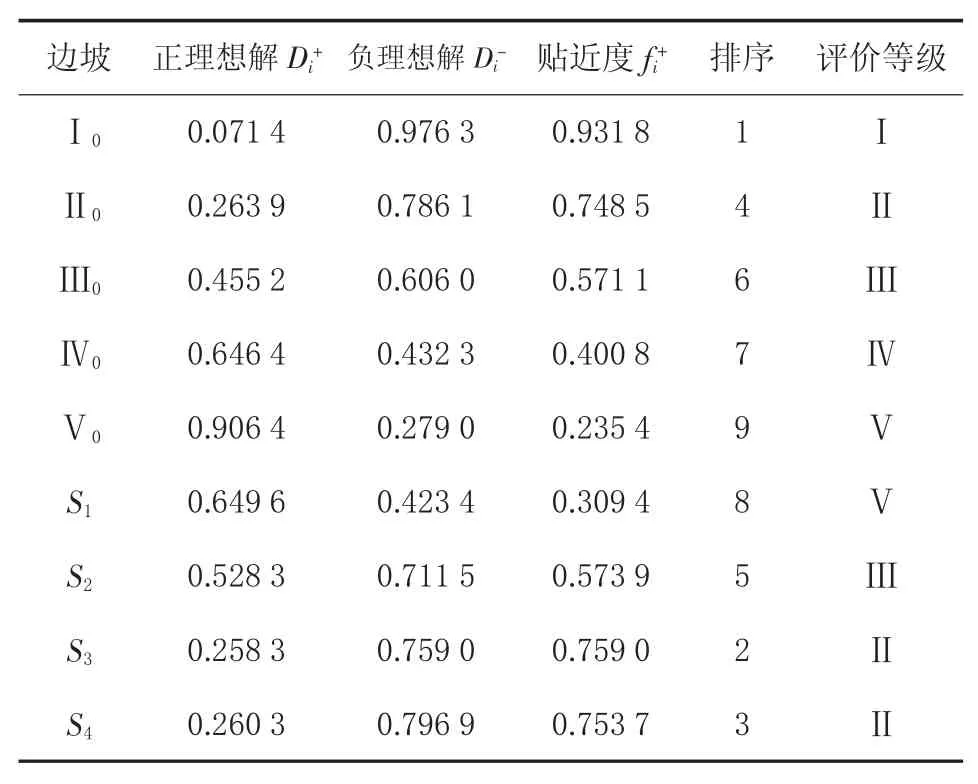
表4　邊坡穩(wěn)定性評價結果

由表4可知，巖土邊坡穩(wěn)定性的貼近度分類區(qū)間為：

將邊坡S1、S2、S3、S4穩(wěn)定性貼進度與上述分類區(qū)間對比可知，S1為極不穩(wěn)定Ⅴ級，S2為基本穩(wěn)定Ⅲ級，S3為較穩(wěn)定Ⅱ級，S4為較穩(wěn)定Ⅱ級。其中S3用灰色關聯(lián)法［6］和可拓評價法［11］評價結果為穩(wěn)定性Ⅰ級，本文判別為較穩(wěn)定Ⅱ級，但結果偏于安全，且該評價方法計算簡單，同時能夠對邊坡穩(wěn)定性程度進行排序。因此，改進的AH P-TOPSIS評價法用于巖土邊坡穩(wěn)定性評價是可行的。

4　結語

（1）采用改進的AH P法計算邊坡穩(wěn)定性各評價指標的權重，降低權重確定的主觀性，避免了傳統(tǒng)9標度層次分析法的一致性檢驗，減少計算量，提高了計算精度，從而提高評價的準確性。

（2）將改進的AH P法與多目標決策理論中的TOPSIS法結合用運到巖土邊坡穩(wěn)定性評價中，AH P法能夠在一定程度上有效地克服TOPSIS法由于因素過多而難以分配權重的弊端，同樣也避免了主觀因素引起的決策失誤，能做出更科學、全面、準確的判斷。通過實例證明了改進模型對邊坡穩(wěn)定性評價的可行性與合理性，且該模型也可應用于其他多指標評價決策系統(tǒng)中。

［1］孫書偉，朱本珍，馬惠民.一種基于模糊理論的區(qū)域性高邊坡穩(wěn)定性評價方法［J］.鐵道學報，2010，32（3）:77-83.

［2］蔡美峰，何滿潮，劉東燕.巖石力學與工程［M］.北京:科學出版社，2002:10-25.

［3］張菊連，沈明榮.高速公路邊坡穩(wěn)定性評價新方法［J］.巖土力學，2011，32（12）：3623-3629.

［4］李云，劉霽.基于模糊集理論與 CSM R的巖質邊坡穩(wěn)定性分析［J］.中南大學學報（自然科學版），2012，43（5）:1940-1946.

［5］張士倫，張孟喜，吉隨旺，等.基于模糊分析的松散體邊坡穩(wěn)定性評價［J］.上海交通大學學報，2015，49（7）：1035-1039.

［6］丁麗宏.基于改進的灰關聯(lián)分析和層次分析法的邊坡穩(wěn)定性研究［J］.巖土力學，2011，32（11）:3437-3441.

［7］趙建軍，賀宇航，黃潤秋，等.基于因子分析法的邊坡穩(wěn)定性評價指標權重［J］.西南交通大學學報，2015，50（2）：325-330.

［8］馮夏庭，王泳嘉，盧世宗.邊坡穩(wěn)定性的神經網絡估計［J］.工程地質學報，1995，3（4）:54-61.

［9］黃志全，崔江利，劉漢東.邊坡穩(wěn)定性預測的混沌神經網絡方法［J］.巖石力學與工程學報，2005，23（22）:3808-3812.

［10］王新民，康虔，秦健春，等.層次分析法-可拓學模型在巖質邊坡穩(wěn)定性安全評價中的應用［J］.中南大學學報（自然科學版），2013，44（6）:2456-2462.

［11］王潤生，李存國，郭立穩(wěn).基于可拓理論的高陡邊坡穩(wěn)定性評價［J］.礦業(yè)安全與環(huán)保，2008，35（6）:25-28.

［12］徐玖平，吳巍.多屬性決策的理論與方法［M］.北京:清華大學出版社，2006:28-30.

［13］吳仲雄，高清平.改進AH P法在采礦方法多目標決策中的應用［J］.礦業(yè)工程，2005，3（5）:18-20.

［14］胡建華，尚俊，龍雷濤.基于RS-TOPSIS法的地下工程巖體質量評價 ［J］.中南大學學報（自然科學版），2012，43（11）：4412-4419.

［15］龔劍，胡乃聯(lián)，崔翔，等.基于AH P-TOPSIS評判模型的巖爆傾向性預測［J］.巖石力學與工程學報，2014，33（7）:1442-1448.

［16］李克鋼，侯克鵬，李旺.指標動態(tài)權重對邊坡穩(wěn)定性的影響研究［J］.巖土力學，2009，30（2）:492-496.

TU457

A

1009-7716（2016）09-0211-05

2016-05-11

姜廷文（1988-），男，甘肅武威人，碩士（在讀），土木工程建造與管理專業(yè)。