多箱截面鋼板剪力墻靜力性能分析

趙滇生,段坤朋

(浙江工業大學建筑工程學院,浙江 杭州 310014 )

?

多箱截面鋼板剪力墻靜力性能分析

趙滇生,段坤朋

(浙江工業大學建筑工程學院,浙江 杭州 310014 )

研究了多箱截面鋼板剪力墻的靜力性能,利用有限元軟件ANSYS分析單塊矩形板模型,計算結果與經典解對比驗證。然后再建立單層和多層多箱截面剪力墻,通過求解水平極限荷載,研究箱室數量和寬厚比對剪力墻靜力性能的影響。

多箱；鋼板剪力墻；靜力性能

鋼板剪力墻興起于20世紀七八十年代,是由周邊梁柱、內嵌鋼板、連接件和加勁肋等組成[1]。在國家提倡大力發展鋼結構建筑的背景之下,鋼板剪力墻具有整體性好,能充分發揮鋼板的各項潛能等優點,是多高層鋼結構中應用前景廣闊的抗側力構件。

多箱截面鋼板剪力墻作為一種新型鋼板剪力墻,其基本結構見圖1。本文著重研究在水平荷載作用下,各項幾何參數對多箱截面鋼板剪力墻靜力性能的影響規律。

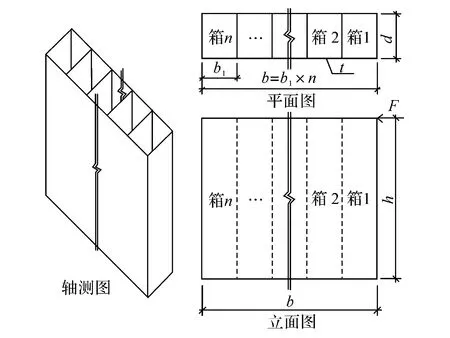
圖1　多箱截面剪力墻示意圖

1　多箱截面鋼板剪力墻的簡化處理和能量法初步分析

多箱截面鋼板剪力墻的簡化計算模型見圖1,在水平荷載的作用下,該模型顯然將在第n箱室處發生局部屈曲,因此對于多箱截面鋼板剪力墻剪切屈曲分析可以簡化為對箱室n外圍鋼板,即長度方向薄板剪切屈曲分析。

均勻受剪矩形板的臨界荷載計算公式[2]為：

(1)

式中：a、h和t分別為矩形板長度、寬度和厚度；

Ks、D和μ分別為板剪切屈曲系數、單位寬度板的抗彎剛度和泊松比。對于四邊簡支的受剪鋼板,Ks按式(2)計算。

(2)

2　計算模型的建立和驗證

采用有限元軟件ANSYS進行分析。鋼板采用SHELL181單元,彈性模量E=206GPa,泊松比μ=0.3。網格密度保證分析能得到穩定的結果[3]。剪力施加在矩形板四周邊上,四邊中間節點剪力為1,四個角點的剪力為1/2,見圖2。邊界條件為約束四邊節點的平面外位移,即自由度3。同時為防止矩形板發生剛體位移[4],約束矩形板中間一點的自由度1和自由度2。彈性計算的結果表明,在圖示荷載的作用下,矩形板處于純剪應力狀態。

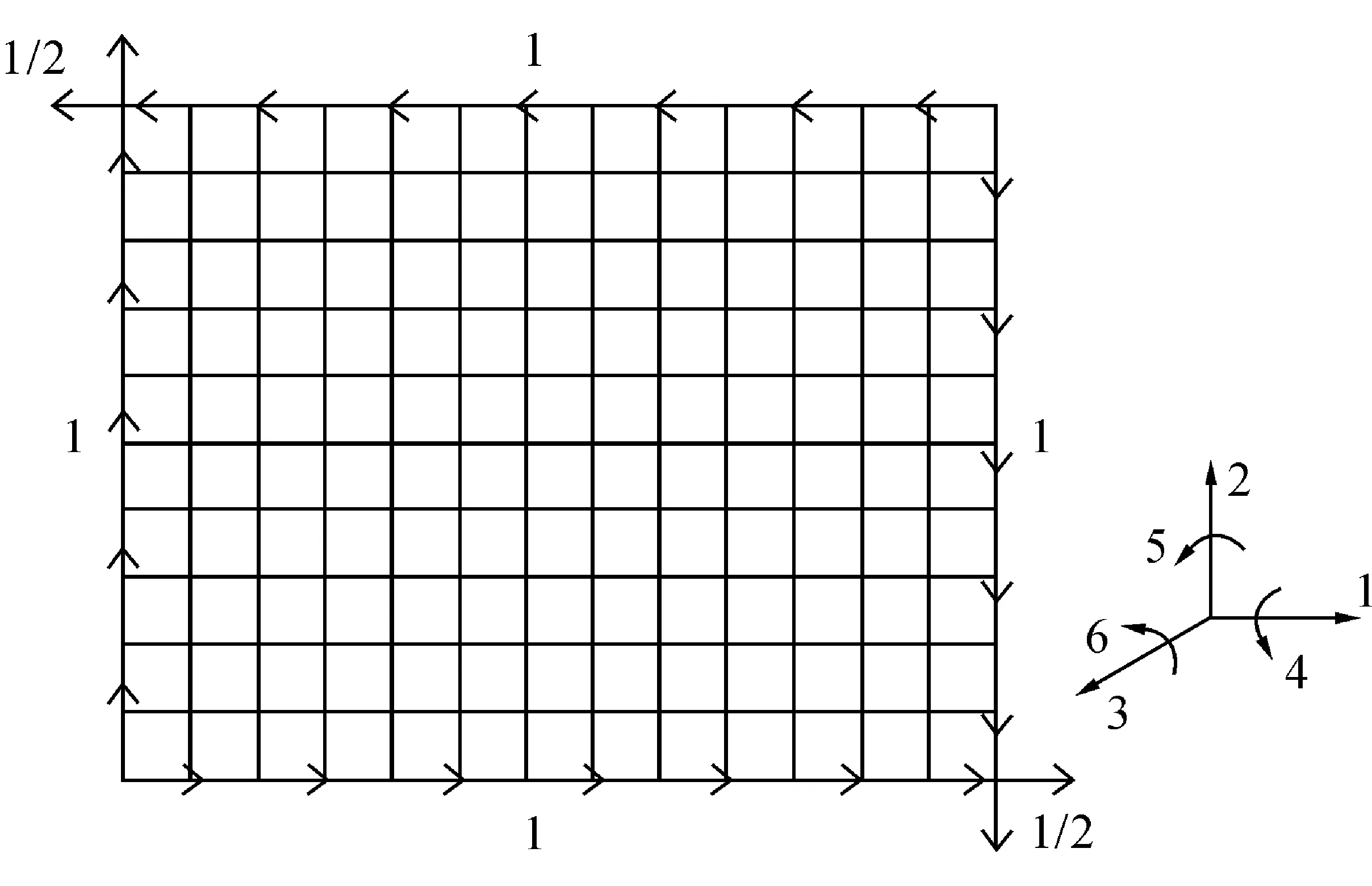
圖2　純剪矩形板加載示意圖

取h=3 000mm,a=3 000mm,t=10mm的四邊簡支矩形板分析。有限元法分析得到的剪切屈曲系數Ks=9.29,而精確理論解為9.34,兩者誤差極小,表明有限元分析過程正確可行。

接著,建立單層建筑多箱截面鋼板剪力墻整體有限元模型分析其靜力性能。取層高h=3 000mm,剪力墻總寬度b=3 000mm,單箱寬度b1=600mm,墻厚度d=200mm,鋼板厚度t=6mm。

由屈曲模態分析可知,多箱截面鋼板剪力墻的屈曲是因局部屈曲而失效,而局部屈曲主要發生在最外邊箱室底部,與前面的預計一致,再次說明用板的剪切屈曲簡化計算多箱截面鋼板剪力墻極限荷載的方法的正確性。另外可以發現,一階屈曲模態圖中局部范圍內屈曲位移較大,其余位置屈曲位移均較小。因此,為提高剪力墻的水平極限承載力,可以在兩側最外箱內設置加勁肋。

3　幾何參數對多層建筑多箱截面鋼板剪力墻靜力性能的影響

圖3　3層建筑多箱截面鋼板剪力墻荷載施加情況

水平極限荷載是衡量剪力墻靜力性能的重要參數,在此著重分析多箱形截面剪力墻的水平極限荷載。考慮實際工程常用尺寸,建立3層建筑多室箱形閉口截面剪力墻模型,荷載施加情況見圖3。并取5箱為標準模型,其水平極限荷載記為Fs,其余模型均是由標準模型改變幾何參數得到。

3.1箱數n的影響

建立多層多室箱形閉口截面有限元模型,其幾何參數及計算結果見表1及圖4,其中Fni表示模型編號為n-i(i=3,4,5,6,7)的水平極限荷載。

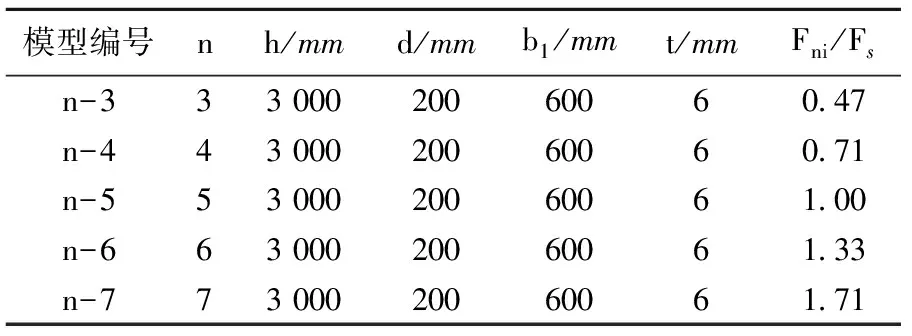
表1　不同箱室數量的有限元分析結果

圖4　箱室數量對剪力墻水平極限荷載的影響

由表1和圖4可知,當其他設計參數不變,隨著多箱截面鋼板剪力墻箱室數量的增加,其水平極限承載力逐漸增加,兩者之間接近線性關系。

當上述模型的鋼板厚度t=10mm,仍然以5箱作為基礎模型,其計算結果曲線見圖4,兩條曲線基本相同,再次驗證箱數對剪力墻水平極限荷載的影響規律。

分析上述現象的原因,是在其他參數不變的情況下,隨著箱室數量的增加,剪力墻總寬度b線性增加,抗彎能力的內力臂和抗剪能力的橫截面呈線性增加,決定剪力墻的水平極限承載力基本呈線性增加。

3.2寬厚比γ的影響

定義寬厚比γ= b1/t,高厚比λ=h/t。建立多層多箱截面剪力墻有限元模型,其幾何參數和計算結果見表2和圖5,其中Fti表示模型編號為t-i(i=5,6,8,10,12,15,20)的水平極限荷載。

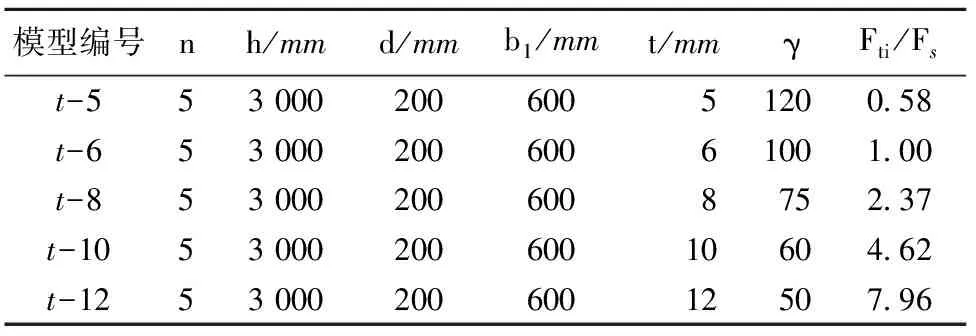
表2　不同寬厚比的有限元分析結果

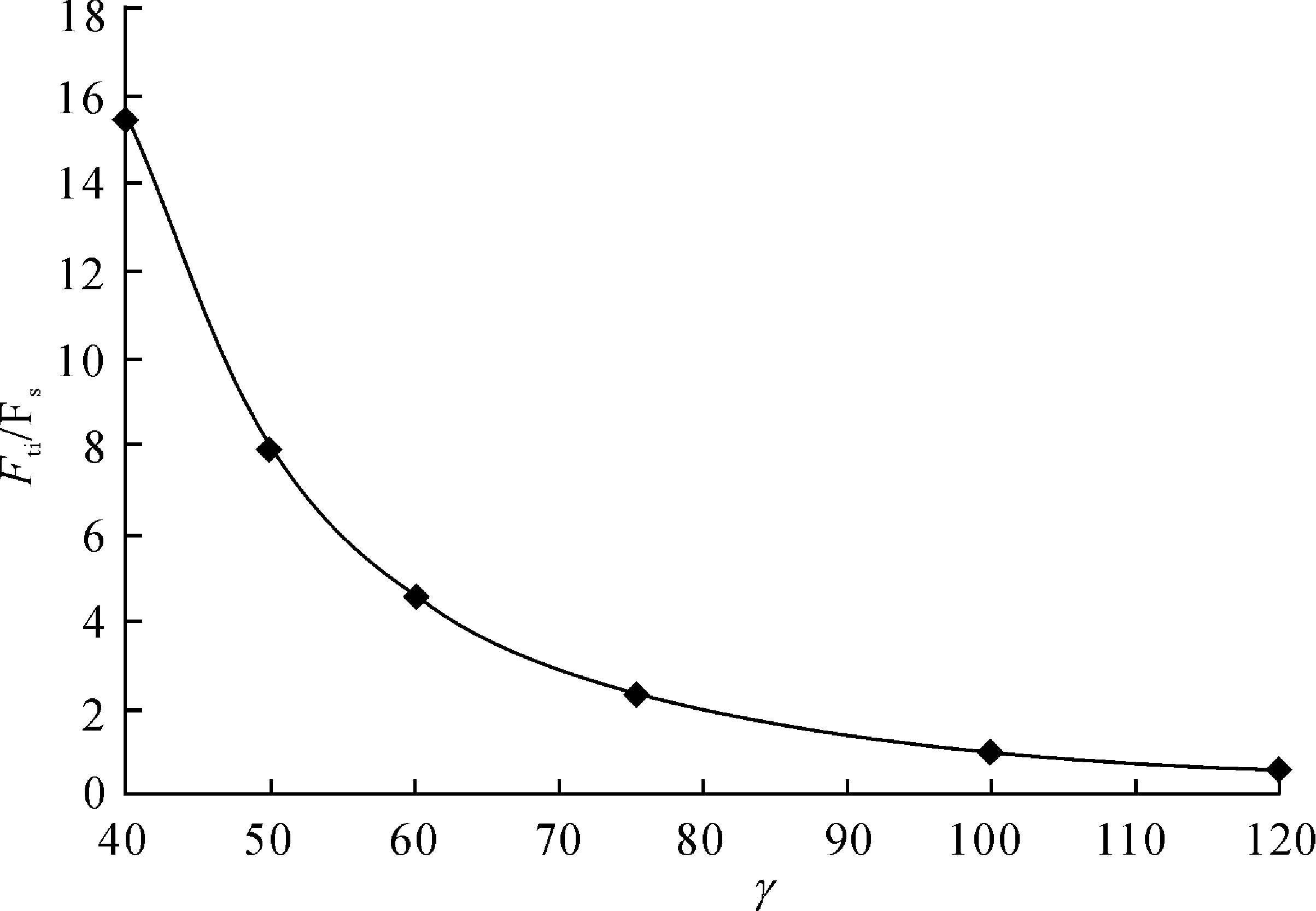
圖5　寬厚比剪力墻水平極限荷載的影響

由表2和圖5可以看出,其他設計參數不變的情況下,隨著寬厚比的降低,多箱截面剪力墻的水平極限荷載逐漸增加。模型t-12水平極限承載力為基礎模型的7.96倍,表明寬厚比的改變對提高多箱截面鋼板剪力墻的水平極限荷載具有顯著的作用。

選取單箱寬度b1=750mm的模型,其厚度變化和上述模型相同,計算結果Fti/Fs與圖5曲線完全相同,再次驗證寬厚比對剪力墻性能的影響規律。

有限元分析結果表明,上述模型的破壞形式,均是由于局部屈曲導致結構整體失效。剪切屈曲應力表達式為

(3)

對多箱截面鋼板剪力墻來說,一般情況下lmax遠大于lmin,以本小節模型為例,(t/lmin)2=1.0×10-4,(t/lmax)2=4×10-6,兩者相差25倍,因此t/lmin,即寬厚比為剪切應力的主要控制項,本文將不再分析高厚比對剪力墻靜力性能的影響。式(3)也解釋了寬厚比對剪力墻靜力性能的影響規律,即隨著寬厚比的降低,多箱截面剪力墻的水平極限荷載逐漸增加。

4　結　語

通過對多箱截面鋼板剪力墻屈曲的水平極限承載力的分析,可以得到以下結論：

1)多箱截面鋼板剪力墻水平極限荷載隨著箱室數量n的增長而增長,且兩者接近線性關系；

2)隨著寬厚比的降低,多箱截面鋼板剪力墻的水平極限荷載逐漸增加,且寬厚比的改變對提高多箱截面鋼板剪力墻的水平極限荷載具有顯著的作用。

[1]DriverRG.Steelplateshearwallnowperformingonmainstage[J].ModernSteelConstruction,2001(9)：48-58．

[2]陳驥.鋼結構穩定理論與設計[M].北京：科學出版社,2014．

[3]趙偉,楊強躍,童根樹. 鋼板剪力墻加勁肋剛度及彈性臨界應力研究[J]. 工程力學,2010,27(6)：15-23.

[4]任濤. 工字梁腹板在局部承壓和剪力作用下的彈性屈曲及極限承載力[D]. 杭州：浙江大學,2005．

Analysis on the Static Performance of the Steel Plate Shear Wall with Multi-Box Section

ZHAO Diansheng, DUAN Kunpeng

2016-04-07

趙滇生 (1957—),男，浙江義烏人，副教授，研究方向為鋼結構、空間結構。

TU

A