可靠性設計分析在聯機檢修領域中的重大突破

丁定浩

可靠性設計分析在聯機檢修領域中的重大突破

丁定浩

在具備聯機檢修的條件下，冗余設計對系統可靠性的提高具有重大的作用。但當前在實際設計上，由于受限于設計的解析模型，因此，只能對雙機并聯結構和N取N-1表決冗余結構進行聯機檢修設計，從而抑制了聯機檢修設計在提升任務可靠性方面的重大潛力。開發了精度滿足工程設計要求的新型數值設計軟件，在聯機檢修設計領域獲得了重大的突破。

停機檢修；定期檢修；聯機檢修；解析模型；數值設計軟件

0　引言

隨著軍用裝備戰術性能的快速提升，裝備變得越來越復雜，從而使系統的任務可靠性面臨著重大的挑戰。系統的冗余設計是大幅度地提升任務可靠度的決定性手段。但當基礎模塊的可靠性過低時，停機檢修的冗余設計則會要求配置過多的冗余單元，考慮到場地和經費的限制，此時此種設計是不合理的。實際上，對于有人值守的場合，聯機檢修的冗余設計更為合理，它是充分地發揮從而大幅度地提升冗余設計的潛力的唯一選擇［1-3］。

目前，只有雙機并聯結構和N取N-1的表決結構才能進行聯機檢修的設計分析，對于多于雙機并聯結構和任意N取K的表決結構，由于缺少顯式的解析模型，因此無法對其進行聯機檢修的設計分析。

原因和詳細的內容，詳見本文附錄。

1　聯機檢修設計的重大突破

由附錄提供的分析可知，要獲取多重單元聯機檢修的冗余設計的解析模型是比較困難的，使用能保證精度的工程設計容許的新型數值設計，是設計分析多重單元聯機檢修系統的唯一出路。

經過研究，其難點已經得到突破，并成功地開發了多重并聯冗余的聯機檢修設計軟件、多重旁待冗余的聯機檢修設計軟件和多個失效單元同時聯機檢修的設計軟件，使聯機檢修冗余設計進入了一個新的實用時期，使任務可靠性有了大幅度提升的可能［4］。

2　數字例

下面例舉數字來示例。

首先，分析數值設計對比模型設計的誤差，但此類比較只能在雙機并聯結構和N取N-1的表決結構中進行，因為得不到其他冗余結構的解析設計模型，從而也就無法對其進行對比。

以修復率為2/h、任務持續工作時間為10 h為例，對通過解析分析和數值分析得到的表1中的不同的并聯結構和表決結構的可靠性及失效率進行比較。表1中的數據說明，通過兩種方式得到的各并聯和表決結構的可靠性的誤差是極低的，相比失效率、修復率參數的誤差完全可以忽略不計。

表1　利用解析分析和數值分析得到的各個冗余結構的可靠性的差別比較

對于不同的并聯和表決結構，在不同的條件下，分別采用停機檢修和聯機檢修的方式對其進行檢修后，其可靠性如表2所示。

從表2可以看出，冗余設計通過聯機檢修后，其效能能夠得到充分的發揮，其失效率比通過停機檢修后的失效率下降了1/46～1/48。

在不同的條件下，3類聯機檢修的可靠性如表3所示，從表3可以看出在相同的條件下，3類聯機檢修中，并聯聯機檢修的可靠性比其他兩類的要低，旁待聯機檢修的可靠性與同時聯機檢修的可靠性則因條件的不同而各有高低，當冗余單元的數量較多時，同時聯機檢修的可靠性高于旁待聯機檢修的可靠性；反之，旁待聯機檢修的可靠性高于同時聯機檢修的可靠性。

表2　停機檢修和聯機檢修后各個冗余結構的可靠性

表3　不同的條件下的3類聯機檢修的可靠性

3　建立在備件保障基礎之上的實際修復率

傳統的修復率僅考慮了故障的修復時間，即僅計及故障檢修、故障隔離、折裝更換和參數校正的時間。這適用于更換對象為元器件的年代，因為當時現場通常備有大量的備件，而當前現場更換單元均為由大量的元器件組成的復雜模塊，不可能隨意地配置，因而傳統的修復率已不再適用。對此，筆者導出了實際的修復率μs與傳統的修復率μ之間的關系，即［5］:

式 （1）中:P（m，nλ，t）——備件數為m、失效率為nλ、備件補充周期為t的備件保障概率。

式 （2）中:tp——現場缺少備件的條件下，等待備件到來的時間。

4　結束語

聯機檢修數值設計分析軟件的成功開發，為大幅度地提升系統的任務可靠性開辟了廣闊的空間，為了普及其應用，我們將竭力地進行義務服務。

［1］丁定浩.聯機檢修的冗余結構使用可用度模型修正 ［J］.電子產品可靠性與環境試驗，2012，30（5）:1-5.

［2］丁定浩.故障檢修方式對裝備現場更換備件配置的影響［J］.電子產品可靠性與環境試驗，2015，33（5）:1-5.

［3］丁定浩.可靠性與維修性工程 ［M］.北京:電子工業出版社，1986.

［4］丁定浩.全壽命周期任務可靠度得到持續保持的新系列設計模型 ［C］//第四屆國防科技工業試驗與測試技術發展戰略高層論壇文集，2012.

［5］丁定浩，陸軍.裝備壽命周期使用保障的理論模型和設計技術 ［M］.北京:電子工業出版社，2011.

附錄：失效率和修復率為常數的聯機檢修可靠度解析模型的導出過程

以兩單元并聯聯機檢修為例，首先列出它出現各狀態之間的相互關系的狀態方程。

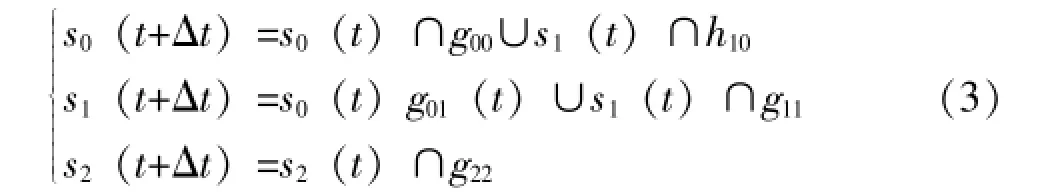
式 （3）中:si（t+Δt）——第i狀態在時刻t+Δt的事件；

si（t）——第i狀態在時刻t的事件；

s0——初始工作狀態，即兩個單元同時處于工作狀態；

s1——兩個單元中已有一個單元發生失效而處于檢修狀態，而另一個單元仍在工作；

s2——兩個單元均處于失效狀態，這說明系統已經失效，一次工作過程已經結束，狀態不再轉移；

gij——t時刻經歷Δt時間間隔因發生故障而由i狀態轉移到j狀態的事件；

hij——t時刻經歷Δt時間間隔因故障修復而由i狀態轉移到j狀態的事件；

A∪B——A、B事件之和，即或者出

現A事件或者出現B事件；

A∩B——A、B事件同時出現的事件。

由此可見，狀態事件方程的第一式表示在t時刻經歷Δt時間間隔后仍處于兩單元正常工作狀態。它是由t時刻兩種可能狀態之一轉移得到的，即:1）兩個單元正常工作，經歷Δt時間間隔不發生轉移，也就是兩個單元均未發生故障；2）在t時刻已有一個單元發生故障，而經歷Δt時間間隔故障單元被修復而重新恢復兩單元同時工作的狀態。

狀態事件方程的第二式表示在t時刻經歷Δt時間間隔后一個單元處于工作狀態，而另一單元處于故障檢修狀態。它也是由t時刻兩種可能狀態之一轉移得到的，即:1）t時刻處于s0態，在經歷Δt時間間隔內一個工作單元發生了故障所致；2）t時刻處于s0態，在經歷Δt時間間隔后，處于工作狀態的單元沒有發生故障，而處于檢修狀態的故障單元也沒有被修復，因而停留在原狀態而未發生轉移。

狀態事件方程的第三式表示在t時刻經歷Δt時間間隔后兩單元均處于故障狀態，這只有一種可能，就是在t時刻系統兩個單元均已發生故障，系統處于失效狀態。在此情況下失效單元的修復時間已與任務可靠度無關，但與戰備完好率直接關聯。

上列狀態方程說明，聯機檢修的任務可靠度，就是s0（t）和s1（t）兩種狀態的概率之和。為了減少工作量，可以只求s2（t）失效狀態的概率，拿1減去s2（t）的概率，即可得到聯機檢修條件下系統的任務可靠度。

為此，對上述各種狀態求取它們的概率，由此狀態方程就轉變為概率方程:

在上列概率方程中，g00、g11和g22等不發生轉移狀態的概率均用相應的轉移狀態的概率來表達，即Pr｛g11｝=1-Pr｛g12｝-Pr｛h10｝，Pr｛g00｝=1-Pr｛g01｝，Pr｛g22｝=1-Pr｛g21｝，但狀態轉移概率Pr｛g21｝等于零，因為已經發生了失效，這一過程已經結束，因此Pr｛g22｝=1。

將上列各等式兩邊同時除以Δt，即可得到下列方程組:

當Δt→0，且失效率和修復率均為常數時，不難理解，狀態轉移事件gij發生的概率為失效率，而hij發生的概率為修復率，即:

由此，上列方程可以轉變成微分方程組:

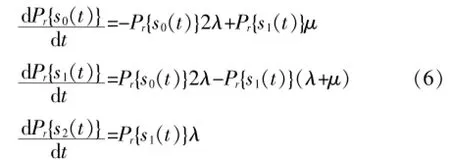
為了易以計算，對上列函數和數值進行拉普拉斯變換，由此可將微分方程組轉換為代數方程組:

在最初時刻，即t=0時，Pr｛s0（0）｝=1，Pr｛s1（0）｝=Pr｛s2（0）｝=0，則上列方程的矩陣形式為:

上列矩陣方程的第一行是求解的目標函數，與它相乘的是等式右邊3個狀態概率在起始時刻的概率參數。實際上狀態轉移矩陣是求解系統任務可靠度的關鍵。掌握了直接建立這一轉移矩陣的方法，就不須經過上述一系列的推導過程。

直接建立轉移矩陣 ［G］的方法，轉移矩陣是一個方陣，首先確定它的階數，這就是系統涉及的狀態數。矩陣中元素等于S加轉移其他相應狀態的概率，元素是轉移相應狀態的概率，前面加以負號，其他不可能出現的狀態元素為0。

以三單元并聯聯機檢修系統的轉移矩陣為例，按上述方法可以直接建立轉移矩陣為:

下面繼續討論前面兩單元并聯聯機檢修的以矩陣表示的求解方法。為此，首先要把前列的矩陣方程的兩邊的右端乘以轉移矩陣的逆矩陣:

則有:

前面已經說過，為了簡化計算，通過求系統的失效概率來求系統的任務可靠度，即:

其中，L-1Pr｛s2（s）｝是失效概率的拉普拉斯反變換，它等于轉移矩陣的逆矩陣中第1項第3列元素，即:

式 （13）中:det［T］——轉移矩陣的行列式；

上列轉移矩陣的行列式為:

代數余子式為:

則系統失效概率的拉普拉斯變式為:

上列表達式無法直接進行拉普拉斯反變換，要求變換為分項分式，即要使

這就可以進行拉普拉斯反變換，得到系統的失效概率為:

不言而喻，s1和s2是s2+（3λ+μ）s+2λ2=0的兩個根，它們等于:

為了求上列分項分式的系數A、B、C，由式A（s-s1）（s-s2）+Bs（s-s2）+Cs（s-s1）=2λ2中以變量s的方次數不同來確定，即前式中左邊的常數等于2λ2，其他有變量s的等于零，即有下列等式成立:

于是系統失效概率的拉普拉斯變式為:

它的反變換，即系統的失效概率Fs（ts）=L-1｛Pr｛s2（s）｝｝為:

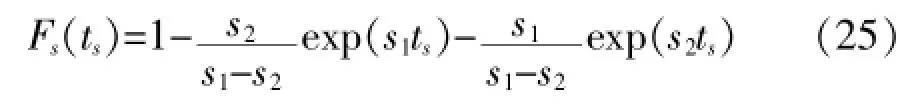
則兩單元并聯的聯機檢修系統的任務可靠度Rs（ts）為:

但是，對于多于兩個并聯聯機檢修系統，系統的任務可靠度卻難以得到解析解。原因在于轉移矩陣的行列式不能分解成分項分式。例如:前面已經直接建立的三單元并聯的聯機檢修系統的轉移矩陣的行列式為:

它的系統失效概率的拉普拉斯變式應為:

其中，s1、s2、s3是方程s3+6λs2+（11λ2-5λμ）s+ 6λ3-9λ2μ=0的3個根，也就是說，對于由n個單元組成的聯機檢修的冗余系統，就要解n次方程的n個根，這種解析解是難以得到的。

解決這一問題的方法是進行數值計算，這就要求開發相應的計算軟件來實現，否則，這類可靠性設計和分析是難以進行的。

A Major Breakthrough of Reliability Design Analysis in the Field of On-line Maintenance

DING Ding-hao

Under the condition of on-line maintenance，the redundant design has a great effect on the improvement of the reliability of the system.But at present，in the actual design，restricted by the analytical model of redundant design，the on-line maintenance design only can be conducted for dual parallel structure and N taking N-1 voting redundant structure，which inhibits the great potential of the on-line maintenance design in improving the reliability of the task.A new type of numerical design software whose precision can meet the requirements of engineering design is developed，and a major breakthrough has been made in the field of on-line maintenance.

downtime maintenance；periodic maintenance；on-line maintenance；analytical model；numerical design software

TB 114.3

A

1672-5468（2016）05-0001-05

10.3969/j.issn.1672-5468.2016.05.001

2016-01-08

丁定浩 （1929-），男，江蘇吳江人，中國電子科技集團公司電子科學研究院研究員，上海大學、南京航空航天大學兼職教授，長期從事系統可靠性、維修性、保障性理論和工程設計研究工作。