考慮供給商品價格的多車場車輛路徑問題

魯建廈，洪歡蕾，陳青豐

(浙江工業大學 工業工程研究所，浙江 杭州 310014)

?

考慮供給商品價格的多車場車輛路徑問題

魯建廈，洪歡蕾，陳青豐

(浙江工業大學 工業工程研究所，浙江 杭州 310014)

針對在煙草、石油和食品等生產配送行業，由于各地生產成本不同，導致商品由不同工廠所生產配送的補給價格存在差異，為了在車輛調度問題中綜合考慮供給成本和運輸成本，并使得總成本最小化，開展了考慮商品供給價格的多車場車輛路徑問題研究.建立了基于分布式生產銷售系統考慮商品供給價格的多點配送車輛路徑優化模型；為了求解優化模型，同時根據考慮供給價格的多車場車輛路徑問題的性質和特征，構造出初始解，并結合8個鄰域結構和局部搜索算法，設計了改進變鄰域搜索算法；最后通過實例，驗證了算法的有效性.

供給價格；多車場車輛路徑問題；變鄰域搜索

多車場車輛路徑問題一直是困擾學者的一類典型的NP難題，由于社會化物流需求不斷提高，物流成本占生產制造成本的比例一直居高不下，因此引起了國家、企業和學術界廣泛的關注.Dantzig等[1]在1959年最早把車輛路徑問題(Vehicle routing problem ，VRP)作為“卡車調度問題”進行研究.

針對多車場車輛路徑問題，Golden等[2]針對MDVRP提出了兩種解決方法，一是改進后的節約里程法，二是“先分配，后路線”的兩階段方法.Cordeau等[3]研究了有時間窗約束的多車場路徑問題(Multiple-depot vehicle routing problem with time window, MDVRPTW)，并提出了統一的禁忌搜索框架.Polacek等[4]使用了變鄰域搜索算法來求解MDVRPTW，在計算過程中，首先采用Cross-Exchange算子產生鄰域解，然后利用加強的3-Opt算子來執行局域搜索.趙燕偉等[5]研究了多車型同時取送貨的多車場低碳路徑問題，并采用了量子進化算法進行求解.魏云飛等[6]研究了非滿載車輛調度問題，提出了免疫遺傳算法.陳曉瞇等[7]研究了需求不確定下的帶時間窗車輛調度問題，并提出了一種混合禁忌搜索算法進行求解.金盼等[8]研究了多目標帶時間窗的多車場車輛路徑問題，并提出了一種全局搜索的混合多目標進化算法.學者們研究這些問題時，假設所有配送中心的補給價格都相同，但實際上，許多生產銷售配送行業普遍存在同樣的商品，各配送中心供應商提供的價格不同.這樣供應價格低的配送中心就應該服務更多的客戶，這樣才可以使供給成本和運輸成本之和在整體上達到最優化.因此在車輛調度問題中應綜合考慮供給成本和運輸成本，使得成本最小化，為此提出了考慮商品供給價格的多車場路徑問題，即每個配送中心提供的商品價格允許存在差異，是另一種MDVRP理論擴展范疇，更符合生產銷售實際需求.

1 考慮供給商品價格的車輛路徑問題建模

1.1 考慮供給商品價格的車輛路徑問題描述

G=(V，E)表示無向連通圖，其中V為無向連通圖中的所有節點集合(包括配送中心和客戶點)，E為網絡中所有弧的集合.目標是在滿足所有客戶點需求及每輛車的裝載量不超過其最大容量的條件下，使得商品的供給成本和運輸路徑成本之和最小.

1.2 問題模型建立

考慮商品供給價格的多車場車輛路徑模型為

(1)

約束條件分別為

(2)

(4)

(5)

(6)

(7)

(8)

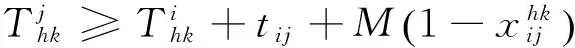
h∈H,WK∈Kh,i∈V,j∈V,i≠j

(9)

(10)

(11)

其中：式(1)為目標函數，由供給成本和配送成本兩部分組成；式(2)表示各配送中心使用車輛的數目低于配送中心所擁有的車輛數目；式(3)表示車輛從配送中心出發并返回原來的配送中心；式(4)表示每個客戶點只能被一輛車服務一次；式(5)確保同一車輛服務同一客戶兩次的情況不存在；式(6)表示車輛不能從一個配送中心到另一個配送中心；式(7)為車輛容量約束；式(8)表示車輛在車場時的時間點等于零；式(9)對于同一車輛服務的兩個用戶，到達后一用戶的時間要大于車輛到達前一用戶的時間點加上兩用戶之間的行駛時間，從而限制子路徑的出現，式(10)為車輛行駛時間約束；式(11)表示車輛到達用戶的時間點大于零.

2 改進變鄰域搜索算法設計

由Mladenovic和Hansen(1997年)提出的變鄰域搜索算法(VNS)屬于啟發式算法，它是局部搜索算法的衍生，多用來求解組合優化問題.針對大規模的VRP問題，VNS算法具有優良的尋優性能，一個有效的啟發式算法，在近幾年的文獻中，被廣泛的用于求解車輛路徑問題.由于傳統的局部搜索算法在迭代的過程中，通常只會設計單個鄰域結構生成鄰域解，再對鄰域解進行局部搜索獲得最優解.單個鄰域結構的設計使得傳統的局部搜索算法很容易陷入局部最優解，導致算法得到全局最優的概率大大降低.所以將設計一個改進的變鄰域搜索算法來解決考慮商品供給價格的多車場車輛路徑問題.

2.1 算法框架設計

圖1為改進變鄰域搜索算法的基本框架.算法的改進之處主要包含以下4個方面：1)初始解的構造階段，首先采用聚類法完成客戶點的分配，然后再用節約算法完成路徑的初始化；2) Shaking過程中，設計了8種不同的鄰域結構，以擴大搜索范圍，同時采用交換算子和插入算子；3)在Local Search過程中，采用2-Opt和Or-Opt兩種算子；4)引入模擬退火算法，用于在一定條件下接受部分較差解，減少算法陷入局部最優的可能性.

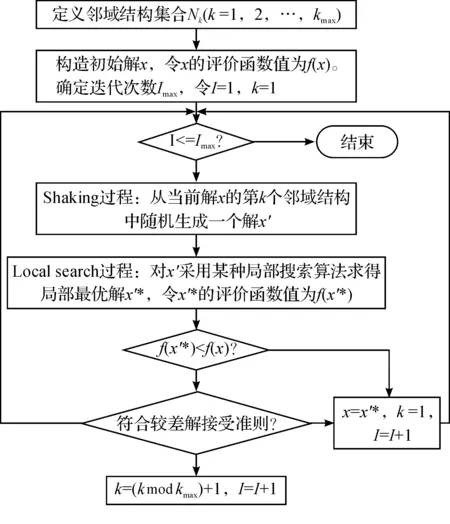
圖1 改進變鄰域算法框架圖Fig.1 Improved VNS flowchart

2.2 初始解的生成

初始解的生成方法為先聚集后路徑的方法.點的聚類過程采用的是類似三標準聚集算法[9]，由于需要同時考慮配送中心供給成本和車輛路徑之間的關系，把供給成本這一因素加入到聚類的構造過程中，在計算平均距離和最近距離時，同時考慮供給成本項.具體聚集流程如下：

Step 1 初始化Nu=N，其中集合Nu為所有沒有聚集的需求點集.

Step 2 重復一下步驟，直到Nu為空.

Step 3 以每個配送中心為中心，包含分配到各配送中心的客戶點構成聚類，配送中心的數量即為聚類的數量.

Step 4 計算平均路徑成本和補給成本之和.計算每個客戶點Ni∈Nu與各個聚類之間的平均距離Lih，并用Cih=Lihβ+Diαh來表達客戶點Ni加入聚類h所增加的成本值.令Ci1為客戶點Ni加入到各個聚類后增加成本最少的聚類，Ci2為增加成本第二少的聚類，從Nu中選取滿足Ci2-Ci1≥0.1Ci2的客戶點組成集合Ns.如果Ns為空，則跳轉至Step 5；否則，從集合Ns中選擇Ci2-Ci1差值最大的客戶點Ni，并將Ni分配至增加成本最少的聚類中，Nu=Nu∕{Ni}，跳轉至Step 2.

Step 5 計算最近距離.對于余下的每個客戶點Ni∈Nu，如果聚類A的某個客戶點與Ni的距離最近，則將Ni分配至聚類A中，Nu=Nu∕{Ni}，跳轉至Step 2.

在點的聚類過程完成后，采用節約算法[9]對每個聚類進行路徑的初始化.

2.3 鄰域結構的設計

Polacek等[4]設計了由12個鄰域結構組成的鄰域結構集合，這個鄰域結構集合針對的問題也是多車場車輛路徑問題，針對每個鄰域結構都指定了相應供應點數和變化子路徑的最大長度，但是其中并沒有指定Shaking過程中的操作算子，由于需要考慮商品供應價格存在差異的特殊性，將對其設計的鄰域結構做相應修改，得到表1所示的鄰域結構.

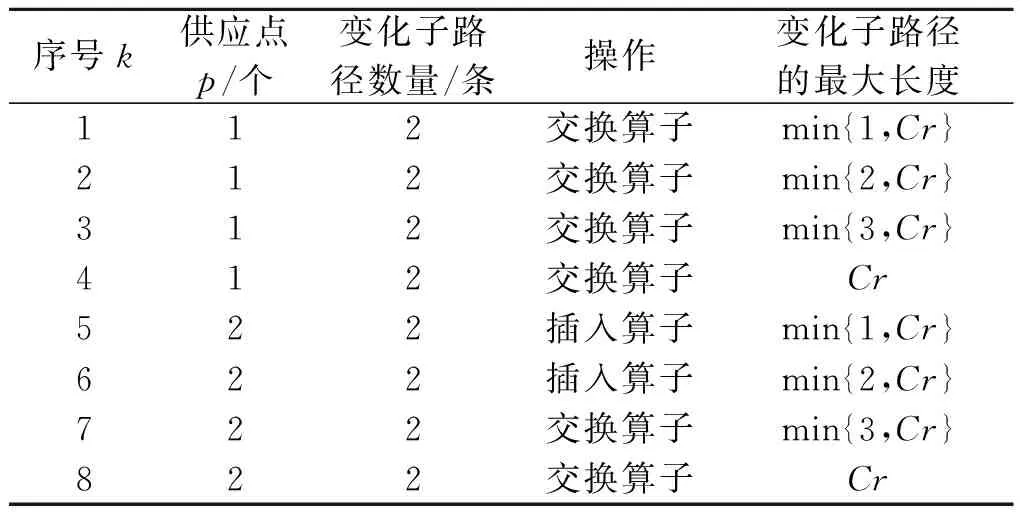
表1 鄰域結構集合1)

注：1)p為參與路徑交換的車場的數量值；Cr為分配給路徑r的客戶點數.

該鄰域結構包含了4個主要度量：1)變化子路徑所屬的供應點p的數量，2)變化子路徑的數量，3)操作算子的選擇，4)變化子路徑的最大長度.由于車輛路徑問題中考慮了貨物的不同供給價格，顯然供給價格低的供應點需要服務更多的客戶點，所以當兩條變化路徑在兩個不同的供應點，并且子路徑長度不大于2時，采用插入算子，被選中的子路徑從供給價格高的路徑插入到供給價格低的路徑中去.

2.4 Shaking過程

Shaking過程的作用主要是通過先前已經設計好的鄰域結構，將當前解經過操作算子變換出一個新的解，來擴展當前解的搜索空間，以降低整個算法陷入局部最優的可能性.Shaking過程并沒有改變當前解的大部分特征，而這也就可以在一定程度上使算法的收斂速度加快.

插入算子包括原序插入和反轉插入，交換算子也可分為原序交換和反轉交換，分別如圖2，3所示，其中Depot代表配送中心.圖2所示插入算子的操作對象為屬于不同配送中心的兩條變換路徑；圖3所示交換算子的兩條變換路徑可以來自同一個配送中心，也可以來自不同的配送中心.Shaking過程中反轉算子的概率一般設置的較小，由于車輛行駛路徑都具有方向性，所以在子路徑的交換過程中都會盡可能保持子路徑的原有方向，以提高獲得可行解的概率.兩種反轉算子的概率都為picross，原序算子的概率為1-picross.picross的取值可以設定為1/K，其中K為所有配送中心擁有車輛的總數.

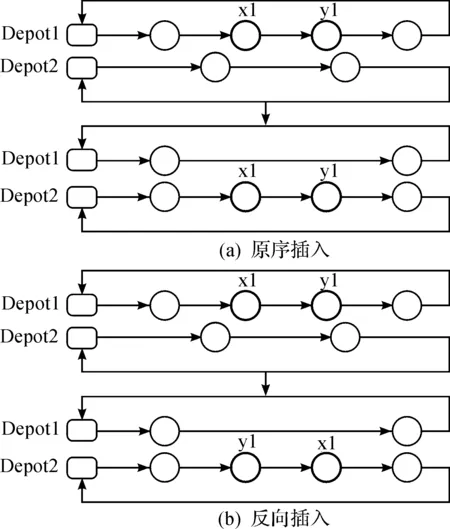
圖2 插入算子操作示例Fig.2 Insert operator

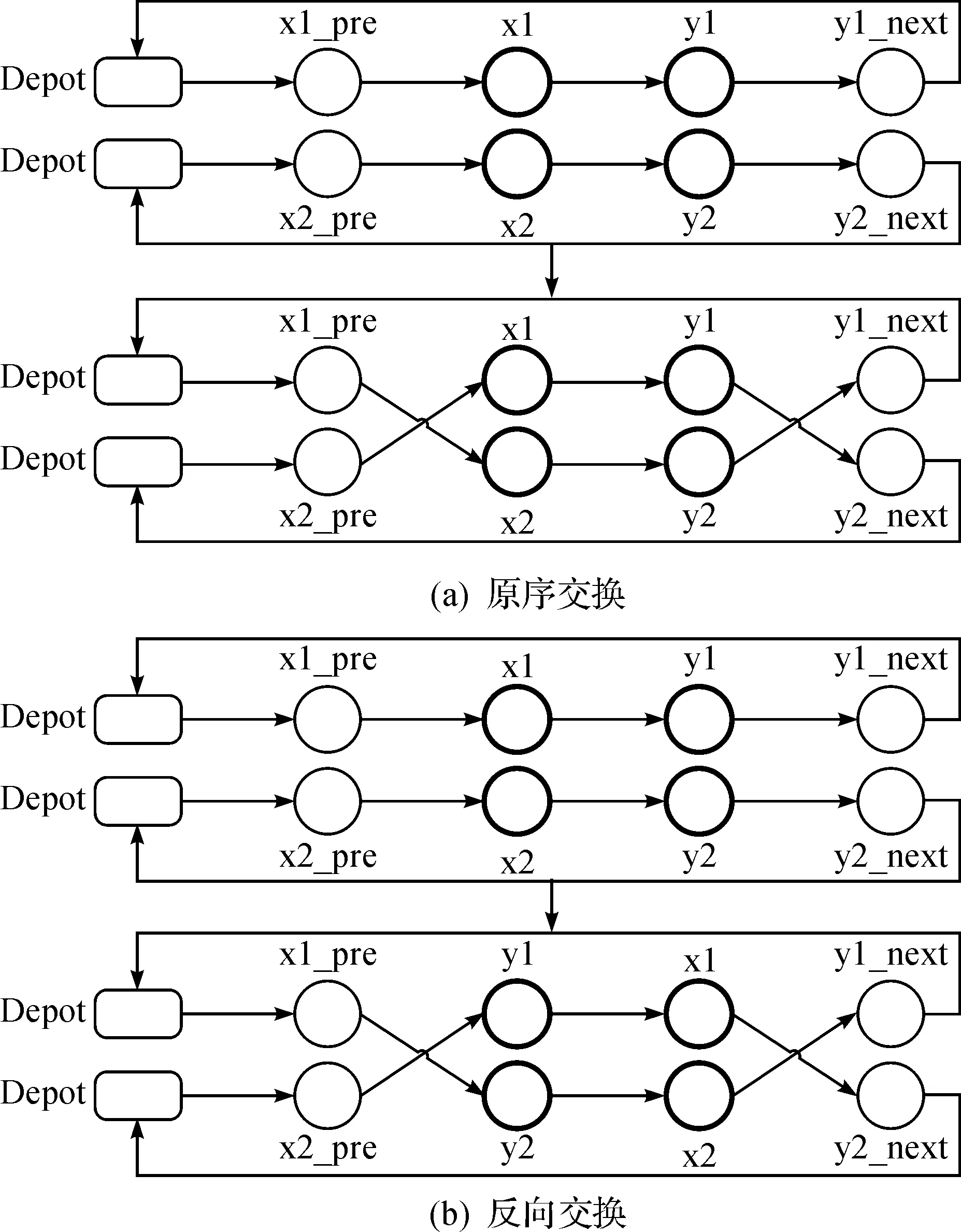
圖3 交換算子操作示例Fig.3 Change operator

2.5 Local Search(局部搜索)過程

局部搜索過程的作用是對Shaking過程中所獲得的兩條新路徑進行局部搜索操作，并分別求出兩條新路徑的最優解，以獲得算法的局部最優解.局部搜索過程最主要的部分是局部搜索算子的設計，好的局部搜索算子能使算法在一個合理的時間內得到較理想的局部最優解，也同時決定了整個變鄰域搜索算法的最終求解效率.

常用的局部搜索算子包括：2-Opt，Or-Opt，3-Opt和2-Opt*等，王征等[7]經過大量實驗顯示：3-Opt獲得的解要優于2-Opt和Or-Opt，但其運行時間往往過長；Or-Opt則可以在較短的時間內獲得求解質量較好的解；2-Opt使得子路徑的方向發生改變，可以尋找反方向的較優解.綜上所述，選擇2-Opt和Or-Opt算子，以達到能在合理時間內獲得較優解的目的.這兩個局部搜索算子的操作示例如圖4所示.每次局部搜索時都需要隨機的選擇一種算子，這里將Or-Opt算子被選中的概率設置為1/2，2-Opt算子被選中的概率則也為1/2.

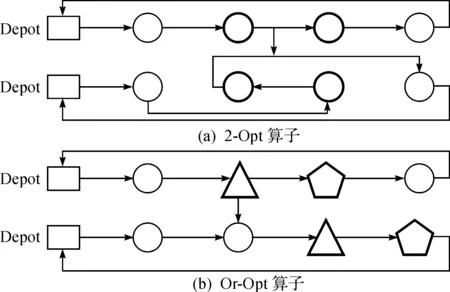
圖4 單路徑局部優化算子操作示意圖Fig.4 Single-path local optimization operator

在Local Search過程中，除了要設計操作算子以外，還要設計算法的局部搜索策略.搜索策略有兩種主要的方式[9]：first-improvement和best-improvement.一般情況下，后者的搜索時間會比前者要短，但是前者的求解質量會比較好.經過前期測試，權衡算法求解時間和求解質量之間的關系，這里采用best-improvement策略.

2.6 較差解接受原則和終止準則

較差解接受原則的設計是為了提高算法對求解空間的一個擾動程度，即在局部搜索過程結束后，可以以一定條件接受較差解，以改善算法過早陷入局部最優的缺陷.這里將通過Chiang等[10]提出的模擬退火算法來設計變鄰域搜索算法的較差解接受原則，使得算法能在一定概率下接受較差解.模擬退火算法中需要設計溫度參數T和每個溫度下迭代的次數IT，設初始狀態T=T0，完成一個內循環，則T每次減少T0(IT/Imax).

為了防止算法運行時間過長，將引用改編CHEN Qingfeng等[11]設計的終止準則.終止準則分為2個部分：首先，設計VNS算法的最大循環次數為1 000次；其次，如果計算機運行時間超過1 800 s，則程序終止.

3 算法檢驗

為了檢驗改進變鄰域搜索算法的有效性，需要設計拉格朗日松弛法求解出原問題的一個下界；同時還需要設計具體的算例，并通過改進變鄰域搜索算法求得的最優解與下界的差值進行比較分析，以此來評價所設計變鄰域搜索算法的有效性.所選算例是在Cordeau標準算例的基礎上，針對考慮商品供給價格的多車場車輛路徑問題的特殊性作出相應修改的計算算例.

3.1 拉格朗日松弛問題

拉格朗日松弛法[12]是通過將約束規劃中造成問題難解的約束吸收到目標函數中，使得問題變得容易求解的一種技術.拉格朗日松弛法可吸收的約束包括3種類型：等式約束、不等式約束和混合型約束.

通過放松原問題的“每個客戶點僅接受一輛車的一次配送”約束條件式(4～6)，利用拉格朗日松弛法法求得松弛問題，建立松弛問題模型，分解拉格朗日松弛問題，建立子問題，采用改進的標號法[12]來求解帶容量約束的子問題，最后用次梯度法[13]解拉格朗日乘子問題，并得到拉格朗日松弛問題的下界.

3.2 算例驗證

試驗部分采用20個Cordeau標準算例的前六個算例進行測試，這6個算例的Depot點數都為4.研究并沒有涉及超過4個Depot點的中大規模問題，主要是因為在拉格朗日松弛問題中設計了回溯的過程，導致中大規模的算例很難在較短的時間范圍內得到松弛問題的下界.變鄰域搜索算法和拉格朗日松弛算法的代碼使用Matlab編寫，算例代碼在個人計算機上運行，運行環境為Intel core i3 AMD2.10 GHz，2 GB RAM.

3.2.1 參數設置

在前期試驗中，經過對算例的多次試驗，以確定算法中的各個參數，以便設計的變鄰域搜索算法在其他算例中能夠獲得較好的最優值.變鄰搜索算法中部分重要參數值如下：算法總的迭代次數為1 000次；局部搜索次數為200次；評價函數中車輛超載的懲罰系數E值為200；抖動過程中反轉算子的選擇概率picross設為0.2；局部搜索過程中的Or-Opt操作算子的選擇概率pOr-Opt設為0.5；4個Depot點的單位供給價格分別為7,8,9,10；車輛的最大容量180；車輛單位距離運輸成本為6.

3.2.2 算例結果與分析

為了驗證所設計的改進變鄰域搜索算法對求解所提出問題的有效性，需要對算例的求解結果與拉格朗日松弛算法的求解結果進行比較，表2給出了拉格朗日松弛方法和變鄰域搜索算法針對Cordeau的6個算例得到的最優解，以及它們所得結果之間的GAP值，其中GAP=(Z2-Z1)/Z2×100.從表2中可以清晰看出：變鄰域搜索算法得到的目標值與拉格朗日松弛下界的差值比值最大時為4.21%，表示與最優目標值比較接近，因此所設計的變鄰域搜索算法在中小規模的問題上可以獲得較好的值.

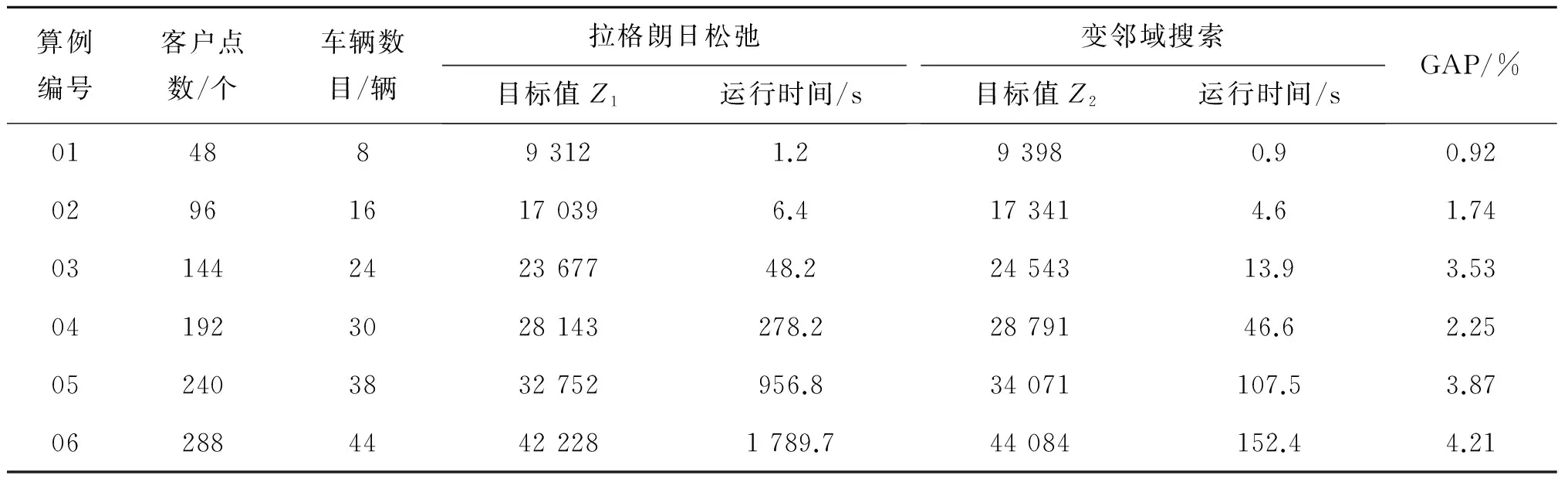
表2 拉格朗日松弛&變鄰域搜索計算結果對比

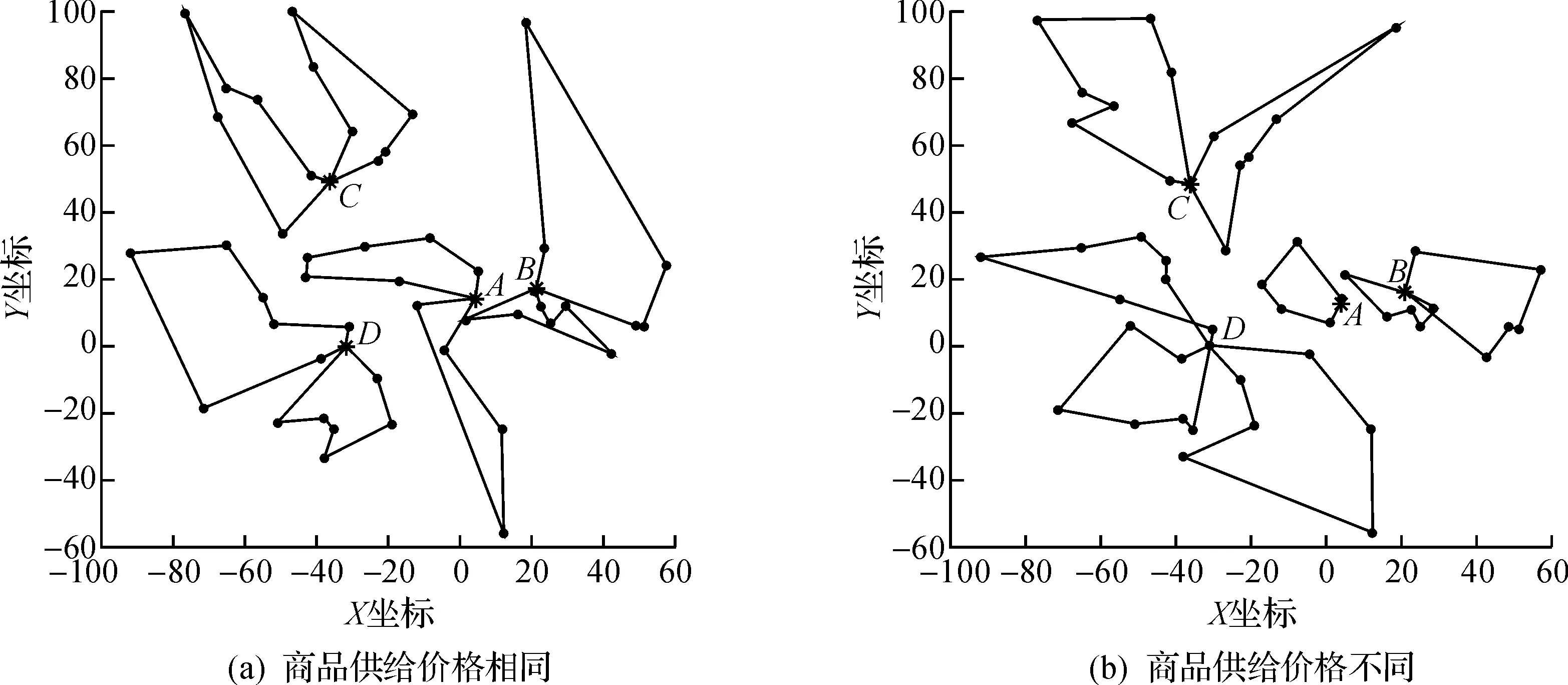
圖5 最優路徑圖Fig.5 Optimal path diagram

圖5中的兩張圖都是算例01經過設計的改進變鄰域搜索算法獲得的最優路徑圖，惟一不一樣的地方是圖5(a)中各Depot點的商品供給價格相同，而圖5(b)中各Depot點的商品供給價格不同.通過對比這兩張圖可以看出各個配送中心補給成本的差異給車輛路徑規劃所帶來的影響.相對于商品供給價格相同的圖5(a，b)中供給價格高的A-Depot點服務的客戶相對變少了，而供給價格低的D-Depot點則服務了更多的客戶點.由此可以看出改進的變鄰域搜索算法對考慮商品供給價格的多車場車輛路徑問題的求解是有效的，并且更加符合實際的車輛運輸問題.

4 結 論

針對石油、煙草和食品等多點分布式生產銷售配送行業商品供給價格不同問題，在車輛調度問題中綜合考慮了供給成本和運輸成本，使得成本最小化，提出了考慮商品供給價格的多車場路徑問題(MDVRP)，研究目的是使貨物供給成本與配送成本的總和最小.建立了考慮商品補給價格的多車場車輛路徑問題模型，該問題模型更加符合實際；設計了改進的變鄰域搜索算法，在算法的Shaking過程中，設計了8中鄰域結構來擴大解的搜索范圍，并且同時采用了插入操作算子和交換操作算了，減少了算法陷入局部最優的可能性，在Local Search過程中采用了2-Opt算子和Or-Opt算子，較好的平衡了求解質量和求解時間之間的關系；通過計算算例來驗證變鄰域搜索算法求解的有效性.研究對于多點分布式生產銷售配送行業具有很好的應用前景.

[1] DANTZIG G B，RAMSER J H. The truck dispatching problem[J]. Management science，1959，6(1)：80-91.

[2] GOLDEN B L，MAGNANTI T L，NGUYEN H Q. Implementing vehicle routing algorithms[J]. Networks，1977，7(2)：113-148.

[3] CORDEAU J F，LAPORTE G，MERCIER A. A unified tabu search heuristic for vehicle routing problems with time windows[J]. Journal of the operational research society，2001，52：928-936.

[4] POLACEK M，HARTL R F，DOERNER K，et al. A variable neighborhood search for the multi depot vehicle routing problem with time windows[J]. Journal of heuristics，2004，10(6)：613-627.

[5] 趙燕偉，李文，張景玲，等.多車型同時取送貨問題的低碳路徑研究[J].浙江工業大學學報，2015，43(1)：18-23.

[6] 魏云飛，黃德才.求解非滿載車輛調度問題的免疫遺傳算法[J].浙江工業大學學報，2005，33(5)：511-515.

[7] 陳曉瞇，孟志青，徐杰.基于混合禁忌搜索算法的動態車輛路徑研究[J].浙江工業大學學報，2009，37(5)：580-585.

[8] 金盼.混合多目標進化算法在帶時間窗車輛路徑問題中的應用[D].杭州：浙江工業大學，2013.

[9] 王征，張俊，王旭坪.多車場帶時間窗車輛路徑問題的變鄰域搜索算法[J].中國管理科學，2011(2)：99-109.

[10] CHIANG W C，RUSSELL R A. Simulated annealing metaheuristics for the vehicle routing problem with time windows[J]. Annals of operations research，1996，63(1)：3-27.

[11] CHEN Qingfeng，LI Kunpeng. Model and algorithm for an unpaired pickup and delivery vehicle routing problem with split loads[J]. Transportation research part E，2014，69(1)：218-235.

[12] 劉泳.基于拉格朗日松弛和分支定界算法的3PL運輸調度問題[D].武漢：華中科技大學，2011.

[13] 陶繼平.基于拉格朗日松弛法的調度算法研究[D].上海：上海交通大學，2014.

(責任編輯：劉 巖)

Model and algorithm for multiple-depot vehicle routing problem with different supply costs

LU Jiansha， HONG Huanlei， CHEN Qingfeng

(Institute of Industrial Engineering， Zhejiang University of Technology， Hangzhou 310014， China)

In some industries, like tobacco, oil and foodstuff, the supply costs can be different due to the different production costs. So in order to obtain an optimal total cost of delivery and supply, we address the multiple-depot vehicle routing problem (MDVRP) with different supply costs. A multiple-depot vehicle routing model is built considering different production costs; In order to solve the mathematical model, an initial solution based on the nature and characteristics of the problem is generated, and the modified variable neighborhood search algorithm (VNS) by combining eight neighborhoods and local improvement method is designed; Finally, an example was given to test the model and algorithm, and the results prove the method is effective.

supply costs; MDVRP; VNS

2016-03-05

浙江省自然科學基金資助項目((LY15G010009))

魯建廈(1963—)，男，浙江余姚人，教授，博士生導師，研究方向為精益生產、生產調度和制造業信息化，E-mail：ljs@zjut.edu.cn.

TP301

A

1006-4303(2016)05-0553-06