基于多道瞬態瑞雷波法的水泥混凝土抗壓強度推定模型研究
沈晨衛
(上海市政工程設計研究總院(集團)有限公司,上海市 200092)
基于多道瞬態瑞雷波法的水泥混凝土抗壓強度推定模型研究
沈晨衛
(上海市政工程設計研究總院(集團)有限公司,上海市 200092)
采用多道瞬態瑞雷波法對不同尺寸的水泥混凝土試件上的振動信號進行采集,利用時域分析法分析振動信號中體波和面波的分離情況,確定了合適的試件尺寸和震源位置,利用相位變換廣義互相關函數法和全波形能量法分別得到了不同齡期水泥混凝土的振動信號的波速和能量衰減因子,結合同條件養生試塊的抗壓強度試驗值,建立了基于波速及衰減因子的強度推定模型,可為水泥混凝土抗壓強度的快速、無損估算提供參考。
水泥混凝土;波速;衰減因子;強度推定模型
0 引言
水泥混凝土是常用的工程材料之一,其質量影響著結構的使用性能和使用壽命。傳統的水泥混凝土力學性能檢測手段通常需要進行破壞取樣和破壞性試驗,費時費力[1]。基于多道瞬態瑞雷波法的水泥混凝土力學性能檢測方法能在不破壞結構的前提下獲得結構的力學性能,既快速又經濟。因此,研究水泥混凝土力學性能和在其中傳播的波的特征參數的關系,對快速無損地檢測水泥混凝土力學性能有重要價值。
瑞雷波沿介質的自由表面傳播,其傳播速度、能量衰減因子等特征參數和介質的力學性能有較好的相關關系[2]。本研究通過分析水泥混凝土中波的傳播速度和衰減特性,結合同條件養生的試塊的抗壓強度值,建立基于波傳播特性的水泥混凝土抗壓強度推定模型,為水泥混凝土強度快速估算提供參考。
1 多道瞬態瑞雷波法的測試原理
介質在一瞬態震源的激勵作用下,其表層會有瑞雷波的傳播,沿傳播方向以一定的間距△L布置(N+1)個檢波器,便可以檢測到N△L長度范圍內的傳播過程[3]。
利用相關算法濾除干擾波的影響后,通過時域分析法人工判斷或者頻域分析法中的相關函數法可以得到傳播時間△t,進而計算得到傳播速度v。
2 試驗方案設計
2.1試驗設備
多道瞬態瑞雷波法測試系統包括震源、檢波器、動態信號分析儀。震源采用橡膠回彈皮錘;檢波器為美國PCB生產的3741B122G/010LN型號的微型加速度計;動態信號分析儀為美國 Data Translation生產的DT9824動態信號分析儀,最高采樣頻率可達4 800 Hz。
2.2試驗方案
瑞雷波和縱波由于波速的差異,傳播一定距離后在時域上某些特征點處會出現分離。試件的尺寸和震源位置是瑞雷波和縱波分離效果的兩個主要影響因素。在不同的位置對三種尺寸的水泥混凝土試塊進行觸發,觀察波形圖中瑞雷波和體波的分離效果,確定分離效果最佳的尺寸和觸發位置,然后澆筑最佳尺寸的混凝土試件和立方體試件,定期采集7 d、14 d、21 d、28 d四個齡期的振動信號,并測試立方體抗壓強度。
混凝土試件的尺寸(長×寬×高)為:300×300× 100,500×500×100,1 000×1 000×100,單位為mm,編號分別為Y-1,Y-2,Y-3。
Y-1~Y-3的傳感器均沿試件中心線布置,震源距第一個傳感器的距離分別為5 cm,15 cm,25 cm,35 cm,45 cm。
為了消除振動信號偏離基線及噪聲的干擾,對Y-1~Y-3采集到的振動信號數據進行消除多項式趨勢項、平滑處理[4],然后觀察瑞雷波和體波的分離效果,如圖1所示。

圖1 Y-1~Y-3波形圖
從圖1可知,Y-1、Y-2信號前部瑞雷波和體波均未出現明顯的分離,Y-3信號前部分離效果較明顯,即當檢波器離震源超過45 cm時,瑞雷波和體波能夠較好地分離。因此確定澆筑Y-3為最佳試驗尺寸。
3 試驗結果分析
利用相位變換廣義互相關函數法計算得到時間延誤,進而求解波速;利用全波形能量法求解出衰減因子。結合同條件養生的混凝土試塊抗壓強度的試驗結果,建立了混凝土抗壓強度推定模型。
3.1波速計算結果
相位變換廣義互相關函數法又稱為PHATGCC方法,相對于其他互相關算法易于實現,計算時間延誤的精度也較高。其算法如下[5]。
假設震源產生離散的信號為S(t),多道傳感器接收到的信號為:
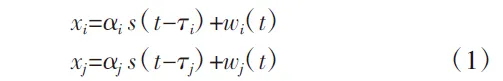
式中:wi(t)、wj(t)為觀測噪聲;xi、xj為第i、j個傳感器接收的信號;τi、τj為信號相對于震源信號的時間延誤,s;αi、αj為衰減系數。
首先計算兩個通道信號間的廣義互相關函數:
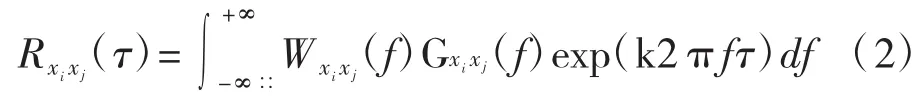
式中:Gxixj(f)為通道i、j信號的互功率譜為加權函數,一般取為互功率譜函數模的倒數:
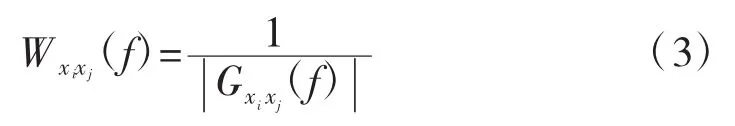
式中:f為頻率,Hz。
然后求取廣義互相關函數的峰值位置:
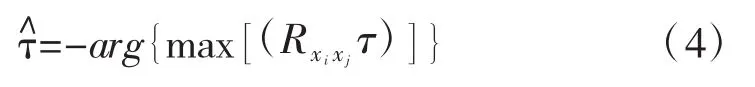
利用MATLAB編程實現了PHAT-GCC算法,計算得到了間距為0.1 m的兩個通道信號之間的時間延誤,進而計算得到了波速,計算結果見表1。
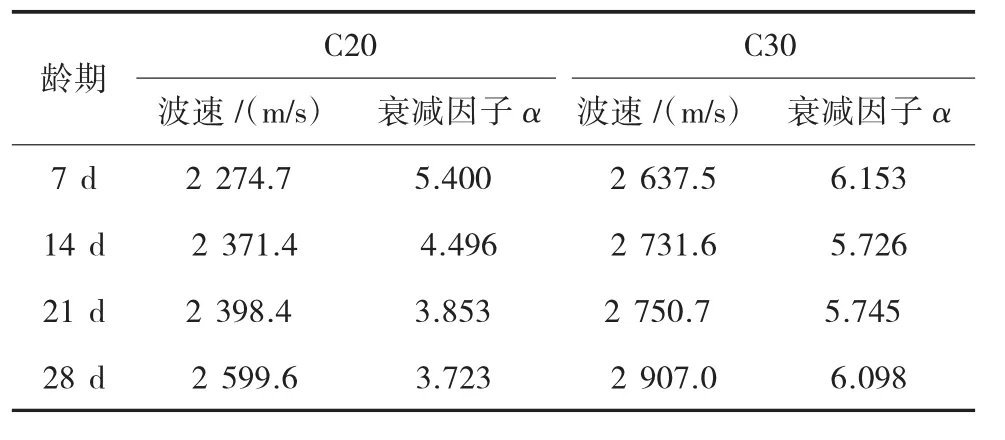
表1 波速及衰減因子計算結果
3.2衰減因子計算結果
瑞雷波在介質中傳播必然會產生衰減,衰減過程用衰減因子來描述,采用全波形能量法計算得到衰減因子。全波形能量值計算見式(5):

式中:E為全波形能量值(g2),g為重力加速度;Vi為第i個采樣點對應的加速度值,g;n為波形長度。
錢驥[6]等假定能量在傳播過程中,其衰減滿足如下指數模型:

式中:Ed為距離震源d處波能量值;E0為震源處的能量值;α為衰減因子。
對小板4個齡期的全波形能量進行如式(6)所示的指數擬合,得到衰減因子,并取10次平行試驗的平均值作為最終的衰減因子a,衰減因子計算結果見表1。
3.3抗壓強度推定模型
根據波速V和衰減因子α,結合同條件養生的水泥混凝土立方體試塊不同齡期的抗壓強度值P,建立了如式(7)和(8)所示的單參數推定模型,和式(9)和式(10)所示的基于波速和衰減因子的雙參數強度推定模型。
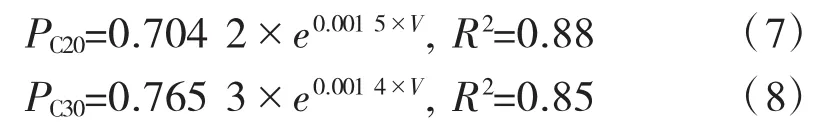
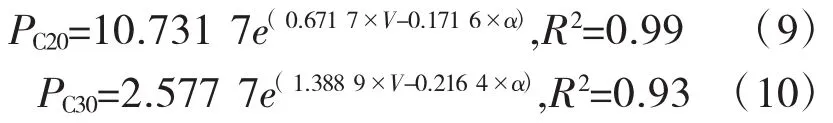
式中:PC20、PC30分別為C20和C30強度推定值。顯然,單參數和雙參數抗壓強度推定模型均具有較高的相關系數。
比較兩種強度推定模型的R2及28 d抗壓強度推定值P預測與實測值P實測的相對誤差ε,來比較兩者的精度,比較結果見表2。
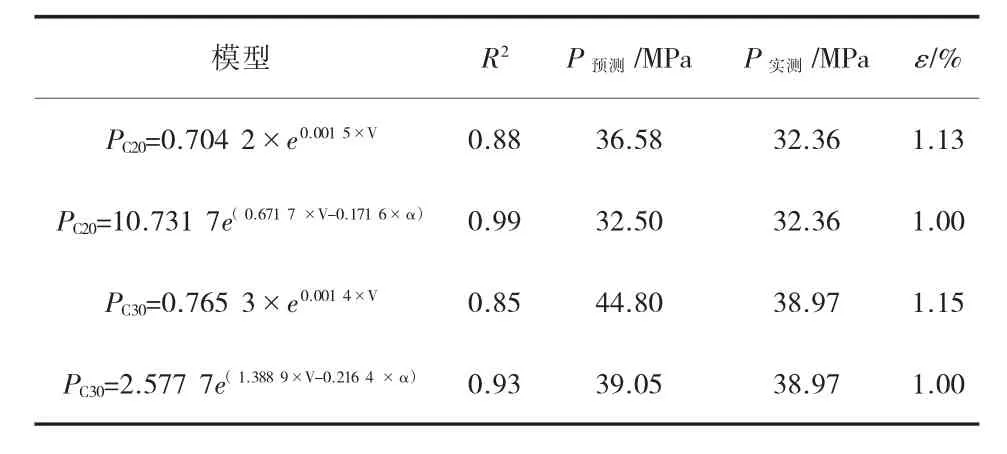
表2 兩種模型的精度對比結果
由表2可知,混凝土小板多參數強度推定模型的R2比單參數模型的大,并且雙參數模型的28 d抗壓強度推定相對誤差小于單參數模型推定的相對誤差,因此雙參數推定模型精度高于單參數模型。
4 結語
本研究采用多道瞬態瑞雷波法研究了水泥混凝土試件尺寸和震源位置對瑞雷波和體波分離效果的影響,發現在長×寬×高為1 m×1 m×0.1 m的混凝土小板上,傳感器距離震源不小于45 cm時,瑞雷波和體波在時域上具有較好的分離效果。利用相位變換廣義互相關函數法計算C20、C30兩個強度等級混凝土小板7 d、14 d、21 d、28 d四個齡期的波速,利用全波形能量法得到對應齡期的衰減因子,基于波速和衰減因子,結合同條件養生試件抗壓強度試驗結果,建立的單參數和雙參數抗壓強度推定模型均具有較高的擬合系數。比較而言,雙參數模型精度更高,兩者均可為混凝土抗壓強度的快速估算提供參考。
[1]吳佳曄.混凝土無損檢測技術的發展現狀及展望[J].四川理工學院學報.2009(4):1-4.
[2]楊成林,時福榮,李從信.應用瑞利波等方法對公路質量進行無損檢測[J].1996(2):3-10.
[3]童立元,陳征宙,方磊,等.瞬態瑞雷波法在工程檢測中的應用研究[J].水文地質工程地質,1999(6):1-3.
[4]王濟,胡曉.MATLAB在振動信號處理中的應用[M].北京:中國水利水電出版社,2006.
[5]王春艷,樊官民,孟杰.基于廣義互相關函數的聲波陣列時延估計算法[J].電聲基礎.2010(8):1-2.
[6]錢驥,孫利民,蔣永.拉索應力波傳播速度與能量衰減特性試驗研究[J].同濟大學學報,2013(11):2-3.
U414
A
1009-7716(2016)07-0291-03
10.16799/j.cnki.csdqyfh.2016.07.087
2016-03-16
沈晨衛(1983-),男,江蘇南通人,工學碩士,工程師,從事道路設計及交通規劃工作。

