VDBA的零-鏡模型及其在符號節點分析中的應用*
李永安
(1.陜西國際商貿學院信息與工程學院,西安712046;2.咸陽師范學院物理與電子工程學院,陜西咸陽712000)
VDBA的零-鏡模型及其在符號節點分析中的應用*
李永安1,2*
(1.陜西國際商貿學院信息與工程學院,西安712046;2.咸陽師范學院物理與電子工程學院,陜西咸陽712000)
為了簡化含電壓差分緩沖放大器(VDBA)電路的符號節點分析,依據零-鏡元件和VDBA的端口電壓電流約束關系,給出了VDBA的12個零-鏡模型以及含零-鏡元件電路的符號節點分析步驟。而且把所提出的模型應用到基于VDBA雙二次濾波器和正交振蕩器的電路分析中,從而簡化了符號節點分析過程。研究結果表明:在符號節點分析中,VDBA的零-鏡模型是系統的、有效的和強大的。
符號節點分析;奇異元件;節點導納方程;電壓差分緩沖放大器
It is well known that the nullator and norator,called nullor elements,play an important role in symbolic nodal analysis[1-4].The symbolic analysis for active circuits becomes easier because of the existence of nullor elements.Recently,symbolic circuit analysis and synthesis have been expanded to the circuits with new active elements,such as current conveyor(CCII),operational trans-conductance amplifiers(OTA),current controlled current conveyor transconductance amplifier(CCCCTA),current differencing trans-conductance amplifier(CDTA),and so on[5-11].The results show that the nullor-mirror models for active devices are conductive to simplifying high-performance circuit analysis.Expanded from OTA,voltage differencing buffered amplifier(VDBA)was described for the first time in 2008[12].A VDBA consists of an OTA with single output and a voltage follower(VF).Since the VDBA has simper structure,it has attracted considerable attention and a number of filters and oscillators using VDBAs have been reported[13-16].It is necessary that using symbolic nodal analysis method analyses the circuits using VDBAs.
1 Pathological Equivalence Models of VDBA
Fig.1 shows the symbols of the VDBA and Eq.(1)presents the corresponding terminal relations[13].

For a VDBA implemented with bipolar technology,the transconductance gain of the VDBA,gm,can be expressed

Here,IBis the bias currents of the device and VTis the thermal voltage.

Fig.1 Circuit symbol of VDBA
The nullor-mirror elements are also referred to as pathological elements,which play an important role in circuit analysis and synthesis.Though the nullor-mirror elements,namely nullor elements and mirror elements,have successfully delineated the CCⅡ,ICCⅡ,OTA,CDBA,and CDTA,they have not been able to described other active elements,for example the VDBA. With this background,on the basis of the equivalence principle that voltage-current constraints for the terminals of the nullor-mirror elements and the VDBA should be the same,we first present 12 nullor-mirror models of the VDBA,as indicated in Fig.2.

Fig.2 12 equivalent models of VDBA
It should be emphasized here that if a grounded norator or current mirror below each model in Fig.2 is elevated off ground,this forms z-copy VDBA,which will be used in multiple-output filters and oscillators.
If one output terminal+z for the VDBA is only required,then the other,+z or-z,is thought to be at ground potential.Moreover,if one input for the VDBA is grounded,the grounded nullator or voltage mirror can be deleted,then,Gmconnecting to the nullator or the voltage mirror should be at virtual ground,resulting in a SISO-VDBA.Then 12 equivalent models for the VDBA simplify to eight ones,as indicated in Fig.3.

Fig.3 Eight equivalent models of VDBA with single input
It may be seen that nullor-mirror models for a VDBA are much more complex than an OTA or a VF.This is due to the fact that a VDBA,consisted of an OTA and a VF,has more complex structure than an OTA or a VF.
2 Applications of Nullor-Mirror Models for VDBA
2.1Approach of Symbolic Nodal Analysis
The approach of symbolic nodal analysis has been generalized to the analysis for analog circuits included voltage mirror and current mirror[2].This method,modified by author,is as follows:
(a)In the circuit included(n+1)nodes,model each active element with its nullor-mirror models;label the grounded node with zero and the other n nodes from one to n;denote independent current sources flowing direction.
(b)Suppress all nullor and mirror elements,write the nodal equation of the circuit:

Here,In=[I1,I2,…,In]T,where Iiis the sum of currents flowing into the ith node from the independent current sources,i=1-n.Vn=[V1,V2,…,Vn]T,where Viis the ith node voltage.Ynis the n×n nodal admittance matrix.
(c)Connect a nullator and a voltage mirror one by one.If a nullator or a voltage mirror is connected between nodes i and j(i<j),then,for the nullator,colj+coli= coli;for the voltage mirror,-colj+coli=coli.At the same time,delete Vjin the Vn.If jth node is at ground,and then delete ith col and Vidirectly from Ynand Vn,respectively.
(d)Connect a norator and a current mirror one by one.If a norator or a current mirror is connected between nodes p and q(p<q),then,for the norator,rowq+ rowp=rowp,Iq+Ip=Ip;for the current mirror,-rowq+rowp= rowp,-Iq+Ip=Ip.At the same time,delete the original Inpin the In.If qth node is at ground,and then delete pth row and Ipdirectly from Ynand In,respectively.
After the above operating process for every pathological element,the nodal admittance matrix Ynof the original network is reduced to Yn-l-m.The new nodal admittance equation is then
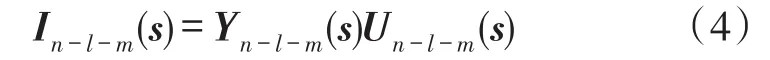
Here,(l+m)is the number of nullators and voltage mirrors or the number of norators and current mirrors.
2.2Symbolic Nodal Analysis for VDBA-Based Circuits
A first example is a VDBA-based quadrature oscillator[16],as shown in Fig.4.

Fig.4 A VDBA-based quadrature oscillator
Since a VDBA has 12 nullor-mirror models,while a VDBA with n or p terminal grounded has eight nullormirror models,then,the nullor-mirror equivalent models of the oscillator have 96 different forms.Fig.5 gives only one nullor-mirror equivalent model.Because of unload at two outputs,the series combination of a nullator and a norator is equivalent to an open circuit,then the circuit in Fig.5 simplifies to the circuit in Fig.6.

Fig5 One of 96 nullor-mirror models for circuit of Fig.4

Fig.6 A reduced model for circuit of Fig.5
Applying the first two steps of symbolic nodal analysis method to the circuit of Fig.6,a(5×5)nodal admittance equation is given by Eq.(5).

Here,I=[0,0,0,0,0]T,this is due to the fact that there are no any independent sources in the oscillators.
Applying the last two steps of symbolic nodal analysis method to Eq.(5),a(2×2)nodal admittance equation is obtained:

Form Eq.(6),one can obtain the characteristic equation as follows

From Eq.(7),the oscillation condition and frequency of the oscillator are

It is clear that the above results are the same as the literature[16].
A second example is a VDBA-based biquad filter[15],as shown in Fig.7.Since a VDBA has 12 nullormirror models,then the nullor-mirror equivalent models of the filter have 144 different forms.Fig.8 gives only one nullor-mirror equivalent mode.

Fig.7 A VDBA-based biquad filter

Fig.8 One of 144 nullor-mirror models for circuit of Fig.7
Note that the current through the norator connected node 8 and ground is zero,then this norator is equivalent to an open circuit.Moreover,the nullator and voltage mirror between nodes 1 and 3 can be merged into a voltage mirror.Similarly,one can delete the norator connected node 9 and ground,then the nullator and voltage mirror between nodes 2 and 4 can also be merged into a voltage mirror.Therefore,the circuit of Fig.8 simplifies to the circuit of Fig.9.

Fig.9 A reduced model for circuit of Fig.8
In order to readily write the nodal admittance equation,adding a conductance G at the input Vi1,and applying the first two steps of symbolic nodal analysis method to the circuit in Fig.9,a(7×7)nodal admittance equation is obtained as

Here,I=[sC1Vi2,sC2Vi3,0,0,0,0,GVi1]Tis an independent current source vector.
Applying the last two steps of symbolic nodal analysis method,Eq.(10)reduces to

Note that V2=Vo,Then transfer function of the filter,which can be derived by solving Eq.(11),is as follows:

It is obvious that the above result is the same as the literature[15].
3 Conclusions
We firstly establish 12 nullor-mirror models for the VDBA in this paper.Symbolic nodal analysis method for analog circuits included pathological elements is systematically stated.Two examples of analog oscillator and filter with VDBAs verify the proposed nullormirror models of the VDBA.The results show that symbolic nodal analysis method is simple,systematic,and powerful in analog circuits with VDBAs.
Acknowledgement
This work is supported by the Natural Science Foundation of Shaanxi Province(2012JM8017).The author would also like to thank the anonymous reviewers for their suggestions.
References:
[1]Saad R A,Soliman A M.A New Approach for Using the Pathological Mirror Element in the Ideal Representation of Active Devices[J].International Journal of Circuit Theory and Applications,2010,38(2):148-178.
[2]Tan L,Liu K,Bai Y,et al.Construction of CDBA and CDTA Behavioral Models and the Applications in Symbolic Circuit Analysis[J].Analog Integrated Circuits and Signal Processing,2013,75(3):517-523.
[3]Wang H Y,Huang W C,Chiang N H.Symbolic Nodal Analysis of Circuits Using Pathological Elements[J].IEEE Transactions on Circuits and Systems Part II,2010,57(11):874-877.
[4]Sanchez-Lopez C,Fernandez F V,Tlelo-Cuautle E,et al.Pathological Element-Based Active Device Models and Their Application to Symbolic Analysis[J].IEEE Transactions on Circuits and Systems Part I,2011,58(6):1282-1395.
[5]李永安.CCCDTA的零-鏡實現及其對正交振蕩器綜合的應用[J].電子器件,2013,36(3):320-324.
[6]趙怡,王衛東.一種基于CMOS CCDVCCⅡ的可編程多功能濾波器及可編程測量放大器[J].電子器件,2011,34(1):53-56.
[7]趙怡,王衛東.一種新型的寬線性范圍差分電壓輸入電流傳輸器及其應用[J].電子器件,2011,34(2):179-183.
[8]李永安,袁戰軍,王贈懿.基于單個CCCCTA接地回轉器的系統綜合[J].電子器件,2015,38(6):1412-1416.
[9]Li Y A.On the Systematic Synthesis of OTA-Based Wien Oscillators[J].AEü-International Journal of Electronics and Communications,2013,67(9):754-760.
[10]Li Y A.Derivation for Current-Mode Wien Oscillators Using CCCCTAs[J].Analog Integrated Circuits and Signal Processing,2015),84(3):479-490.
[11]Li Y A.NAM Expansion Method for Systematic Synthesis of Floating Gyrators Using CCCCTAs[J].Analog Integrated Circuits and Signal Processing,2015,82(3):733-743.
[12]段吉海,郝強宇,徐衛林,等.一種適用于心電信號檢測的高階連續時間OTA-C濾波器設計[J].電子器件,2015,38(4):774-778.
[13]Yesil A,Ka?ar F,Gürkan K.Lossless Grounded Inductance Simulator Employing Single VDBA and Its Experimental Band-Pass Filter Application[J].AEü-International Journal of Electronics and Communications,2014,68(2):143-150.
[14]Sotner R,Jerabek J,Herencsar N.Voltage Differencing Buffered/ Inverted Amplifiers and Their Applications for Signal Generation[J].Radioengineering,2013,22(2):490-504.
[15]Kacar F,Yesil A,Noori A.New CMOS Realization of Voltage Differencing Buffered Amplifier and Its Biquad Filter Applications[J].Radioengineering,2012,21(1):333-339.
[16]Bajer J,Biolek D,Biolkova V,et al.Voltage-Mode Balanced-Outputs Quadrature Oscillator Using FB-VDBAs[C]//International Conference on Microelectronics,Cairo(Italy),2010:491-494.

李永安(1961-),男,陜西三原人,1983年畢業于西北大學物理系。現為咸陽師范學院物理與電子工程學院教授,研究領域為電流模電路的分析與綜合設計,lya6189@tom.com。
Nullor-Mirror Models of VDBA and Applications in Symbolic Nodal Analysis*
LI Yong'an1,2*
(1.School of Information and Engineering,Shaanxi Institute of International Trade&Commerce,Xi'an 712046,China;2.School of Physics and Electronic Engineering,Xianyang Normal University,Xianyang Shaanxi 712000,China)
To simplify the symbolic nodal analysis about the circuits employing voltage differencing buffered amplifiers(VDBAs),according to the terminal voltage-current constraints for the nullor-mirror elements as well as the terminal relations of the VDBA,12 nullor-mirror models for the VDBA and the related procedure of symbolic nodal analysis are presented in this paper.Furthermore,the proposed models are applied to a VDBA-based biquad filter and a quadrature oscillator to simplify nodal analysis process.The results show that the nullor-mirror models for the VDBA are systematic,effective and powerful in symbolic nodal analysis.
symbolic nodal analysis;pathological elements;nodal admittance equation;VDBA
TN713
A
1005-9490(2016)05-1082-05
項目來源:Natural Science Foundation of Shaanxi Province(2012JM8017)
2015-10-15修改日期:2015-11-13
EEACC:113010.3969/j.issn.1005-9490.2016.05.013

