Lipschitz非線性系統觀測器設計方法
◎馬晴 孫偉 賈雪松
Lipschitz非線性系統觀測器設計方法
◎馬晴 孫偉 賈雪松
針對一類滿足Lipschitz條件的非線性系統,研究了輸出對狀態為非線性時的情況下,Luenberger型觀測器的設計問題,給出了判斷觀測器穩定的充分條件,并利用LMI技術選取觀測器的增益矩陣,最后,利用Simulink對該情況下的系統及其觀測器進行仿真,實現狀態的準確觀測。
目前,線性系統的觀測器設計問題已經較為完善,而非線性系統觀測器的設計還沒有一個通用方法,通常是針對不同情形采用不同方法。
許多實際的非線性系統都是全部或局部滿足Lipschitz條件,它們作為一類特殊的非線性系統,其狀態觀測器設計是由Thau首次提出,并給出了觀測器的具體形式和漸進穩定的充分條件。
本文在文獻中利用LMI技術選取反饋增益矩陣的方法的基礎上,研究一類具有普遍形式的輸出相對狀態為非線性的Lipschitz非線性系統,并通過Simulink仿真實現該系統的狀態觀測。
一類Lipschitz非線性系統及其狀態觀測器
對某Lipschitz非線性系統,描述如下:


其中γ為相應的Lipschitz常數。
對該系統設計Lue nberger型觀測器如下:
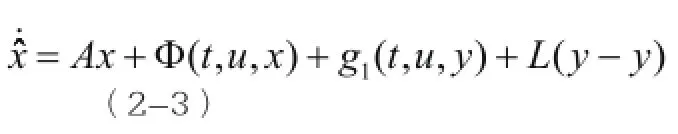
由中的定理可知,式(2-3)給出的觀測器就可保證動態誤差是漸進穩定的。
輸出相對狀態為非線性的Lipschitz非線性系統及其觀測器
將輸出相對狀態為線性時的方法推廣到輸出相對于狀態為非線性時的情形,并對原系統和觀測器進行仿真,實現準確狀態觀測。
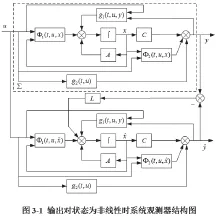
系統與狀態觀測器的描述。針對輸出相對于狀態為非線性時的Lipschitz非線性系統,設計Luenberger型觀測器如下,結構如圖3-1所示:

觀測器的動態誤差為:

該觀測器的設計實質就是選擇合理的增益矩陣使動態誤差(3-2)漸進穩定。
由文獻中定理可知,式(3-1)給出的觀測器可確保動態誤差(3-2)是漸進穩定的。

在總結文獻[4]中將代數Riccati方程的正定解問題轉化為一組線性矩陣不等式的可行性問題的方法基礎上,利用Matlab中LMI工具箱的feasp函數,獲得增益矩陣L。
仿真。考慮一輸出相對狀態為非線性的Lipschitz非線性系統,各參數取值如下:
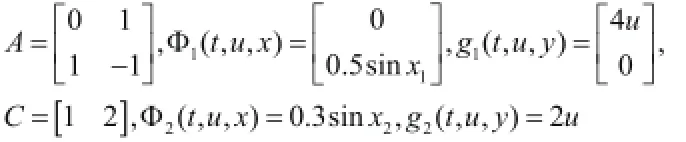
顯然γ1=0.5,γ2=0.3。利用LMI求解,可得:L=[1.4180.386]T。
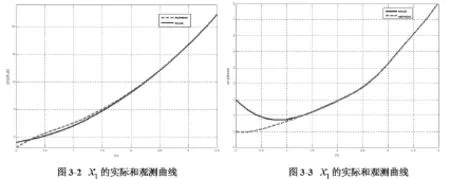
將所得增益矩陣L 帶入到觀測器(3-1)中,給定輸入是振幅為1的sine wave,圖3-2是狀態 x1在初始值時的實際和估計曲線,圖3-3是狀態x2在初始值時的實際和估計曲線。橫坐標為時間,縱坐標為振幅,實線是真實值曲線,虛線是觀測值曲線。
由上圖可見,開始幾秒內,觀測器的狀態不與原系統狀態完全一致,但能很快跟蹤原系統,達到狀態誤差逐漸趨于零,成功利用LMI技術對輸出對狀態為非線性的Lipschitz系統設計了一個能夠快速跟蹤原系統Luenberger型狀態觀測器。
本文根據系統輸出與狀態的關系,研究了一類Lipschitz非線性系統在輸出對狀態為非線性時,系統的一般形式及其Luenberger型觀測器的設計,并利用LMI技術,較好的解決了此類系統的觀測器增益矩陣L的選取問題,最后通過仿真,實現了對系統的準確觀測。
(作者單位:沈陽城市建設學院)

