兩類改進非線性濾波器UKF算法綜述

賈文哲 王劍平

(昆明理工大學信息工程與自動化學院，昆明 650504)

兩類改進非線性濾波器UKF算法綜述

賈文哲 王劍平

(昆明理工大學信息工程與自動化學院，昆明 650504)

通過對卡爾曼濾波的發展進行簡述，引出標準無跡卡爾曼濾波和標準無跡變換的采樣策略。通過對標準無跡卡爾曼濾波的分析，從兩個切入點對標準無跡卡爾曼濾波進行改進,即超球體采樣平方根無跡卡爾曼濾波和強跟蹤無跡卡爾曼濾波，給出了對應的詳細算法，并對無跡卡爾曼濾波算法進行總結與評述。

無跡卡爾曼濾波 采樣策略 超球體平方根無跡卡爾曼濾波 強跟蹤無跡卡爾曼濾波

1960年，美國數學家卡爾曼提出一種濾波方法，將其命名為卡爾曼濾波[1]。卡爾曼濾波的基本思想是將噪聲融入系統的狀態空間模型之中，對前一時刻采用估計的辦法獲得其估計值，對現在時刻采用其測量值，利用相關公式去預估計下一個狀態的估計值。卡爾曼濾波是在維納濾波的基礎之上，利用線性最小二乘法求出系統狀態估計的最優值[2]。因為是以線性最小二乘法為契機，當處理非線性系統時不能應用，但現實中幾乎沒有線性系統，很多非線性因素也不能忽略[3,4]。為了解決卡爾曼濾波在非線性系統中的使用障礙[5]，經過研究，Bucy等學者利用泰勒公式將非線性系統展開成泰勒的一階形式，使它得到近似的線性化，這樣再按照線性卡爾曼濾波的方法處理問題。該方法被命名為擴展卡爾曼濾波[6](Extended Kalman Filtering,EKF)。但該方法在非線性較大時精度不夠，易失去穩定性。此后，Julier S J等提出了無跡Kalman濾波(Unscented Kalman Filter,UKF)，它是以無跡變換為基礎，摒棄了擴展卡爾曼濾波將非線性系統線性化的做法，更好地處理了非線性化問題，同時提高了精度[7]。

1 標準UKF濾波①

標準UKF以標準無跡變換為基礎，無跡變換的規則是在原有的狀態分布的點集之中，采用一種規則選取一些采樣點，保證所選點的均值和協方差與原狀態點集均值和協方差相等，將采樣點代入非線性系統之中，通過這些點集的變換，再求均值和協方差[8]。

給定一非線性離散系統：

(1)

定義Xk、Zk為系統的狀態向量和量測向量矩陣；wk、vk為噪聲觀測值和量測值，wk～(0,Qk)，vk～(0,Rk)，將所述噪聲規定為高斯白噪聲，Q、R分別為其方差。

初始化估計值和狀態協方差矩陣：

(2)

Sigma點計算：

(3)

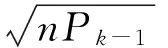
一步預測及其協方差矩陣時間更新：

ξi,k|k-1=f(ξi,k-1),i=0,1,…,2n

(4)

(5)

(6)

(7)

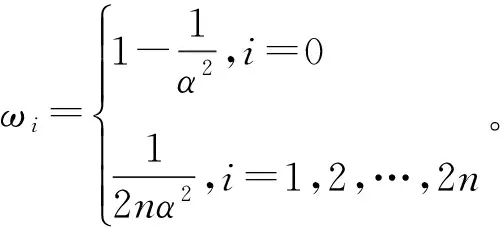
量測更新：

(8)

(9)

(10)

(11)

(12)

2 超球體采樣平方根UKF(SR-UKF)

SR-UKF是在UKF算法的基礎上采用一個狀態協方差矩陣的方根矩陣形式[9～11]，根據QR分解、Cholesky一階更新和最小二乘法，在濾波過程中求出狀態協方差矩陣的平方根，將所得值不斷進行迭代，不再每一個時刻都對矩陣進行再分解，有效防止協方差矩陣非正定的發生[12]。在進行Sigma點選取時，采用超球體采樣策略代替標準無跡變換可以有效地減少計算量。

選擇0≤W0≤1。確定Sigma權值：

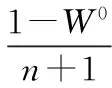
(13)

(14)

其中，α(0≤α≤1)為縮放因子，通過α可以控制采樣點與均值的距離。

初始化向量序列：

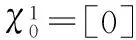
(15)

當輸入維數為j(j=2,…,n)時，迭代公式為：

(16)

其中，i是采樣點順序。

定義如下：

(17)

(18)

其中，β(β≥0)是非負加權項。

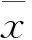
(19)

SR-UKF的算法如下：

a. 初始化；

b. 計算Sigma點；

c. 時間更新；

d. 量測更新方程。

步驟a采用的公式為：

(20)

其中規定矩陣下三

角Cholesky分解運算簡寫成chol()。

步驟b采用的公式為：

(21)

步驟c采用的公式為：

(22)

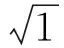
步驟d的公式為：

(23)

采用協方差陣的平方根形式Sx代替協方差矩陣Px參加遞推運算，可以有效提高濾波算法的數值穩定性[14]。

3 強跟蹤UKF

由于標準UKF算法缺乏對系統狀態異常的自適應調整能力，導致濾波精度降低[15]。文獻[15]提出一種改進的強跟蹤UKF算法，該算法采用假設檢驗的方法對異常狀態進行檢測，當系統狀態發生異常時，對預測協方差陣引入次優漸消因子[16,17]自適應地調整濾波增益，實現對系統真實狀態的強跟蹤。該算法中次優漸消因子的確定無需計算系統模型的雅克比矩陣。

強跟蹤濾波器(Strong Tracking Filter，STF)的概念是根據新息向量的正交性原理提出的。這種濾波器與通常采用的濾波器相比，主要表現在它具有較強的關于模型參數失配的魯棒性，同時對于噪聲和初值統計特性的敏感性較低，當有突變狀態產生時，STF具有極強的跟蹤能力，同時在達到濾波定后，這種跟蹤能力依然能夠繼續保持下去，與標準的UKF相比，STF的計算復雜性很低[18～20]。基于以上結論，可以將STF與標準的UKF結合起來，彌補標準UKF魯棒性不足和對突變抵抗性差的問題。

將次優漸消因子λk引入預測協方差陣Pk|k-1以提高自適應能力：

(24)

計算新息序列：

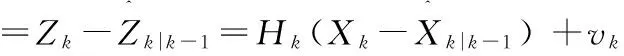
(25)

(26)

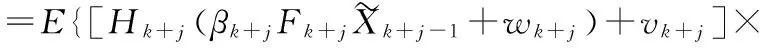
(27)

令Vi=0，最終可得：

(28)

將式(28)代入式(24)可得：

(29)

其中V0為STF實際輸出的基于新息的協方差矩陣，可根據下式計算：

(30)

其中，ρ為遺忘因子，0<ρ≤1，通常取為0.95。

強跟蹤濾波UKF算法流程如下[21]：

a. 按式(2)對式(1)進行初始化；

b. 按式(3)進行Sigma點采集；

c. 按式(4)、(5)進行一步預測；

d. 如果有異常協方差矩陣采用式(24)，如果沒有則采用式(6)；

e. 按式(8)～(12)進行其余的計算。

4 結束語

目前對UKF的改進方法有很多種，除了筆者提到的兩種外，還有將小波變換與UKF算法進行融合、UKF算法的自適應采樣平方根策略及雙UKF算法等。在不同的系統、不同的條件、不同的場合下,應選擇不同的改進方法，完全適用于任何系統的算法是不存在的,很多算法都是在彼此的基礎上進行改進,相輔相成,互相配合，具體選擇哪種算法,還應根據實際的系統來決定。

[1] Kalamn R E.A New Approach to Linear Filtering and Prediction Problems[J].Transactions of the ASME-Journal of Basic Engineering,1960,(82):35～45.

[2] 王慧鋒,吳中相.卡爾曼濾波器在儲罐液位監控系統中的應用[J].化工自動化及儀表,2014,41(7):758～761.

[3] 黃小平，王巖.卡爾曼濾波原理及應用[M].北京：電子工業出版社，2015：4～6.

[4] Wiener N. Extrapolation, Interpolation,and Smoothing of Stationary Time Series[M].Cambridge,Massachusetts：MIT Press,1964.

[5] 劉毛毛，秦品樂，呂國宏，等.基于多新息理論的EKF改進算法[J].計算機應用研究，2015,32(5):1568～1571.

[6] 王秋平,韓磊,張淼,等.觀測時滯離散系統卡爾曼濾波算法[J].化工自動化及儀表,2015,42(10)：1099～1103.

[7] Julier S J,Uhlmann J K,Durrant-Whyte H F.A New Approach for Filtering Nonlinear Systems[C].Proceedings of the American Control Conference. Washington,USA:IEEE,1995:1628～1632.

[8] 甘旭升，叢偉，薛博文，等.基于改進無跡Kalman濾波的小波網絡算法及其應用[J].昆明理工大學學報(自然科學版),2012,37(1):30～35.

[9] 吳江飛,黃珹.一種采樣型平方根濾波及其應用[J].武漢大學學報(信息科學版),2007,32(8):696～698.

[10] 張鵬.基于卡爾曼濾波的航空發動機故障診斷技術研究[D].南京:南京航空航天大學,2008.

[11] 胡永浩，王養柱，趙啟兵，等.SINS靜基座初始對準的超球體采樣STFUKF算法[J].電光與控制，2012,19(4)：59～63.

[12] 楊少委，張旭東.基于SR-UKF的高動態GPS信號參數估計[J].通信技術，2010,43(9)：9～11.

[13] 李光.視頻目標跟蹤濾波算法研究[D].西安：西安電子科技大學,2009.

[14] 李丹，劉建業，熊智，等.基于最小偏度采樣的衛星自主導航SRUKF算法[J].南京航空航天大學學報，2009,41(1):54～58.

[15] 楊文博，李少遠.基于強跟蹤UKF的航天器自主導航間接量測濾波算法[J].系統工程與電子技術，2011，33(11)：2485～2491.

[16] 錢華明，黃蔚，孫龍，等.基于多重次漸消因子的強跟蹤UKF姿態估計[J].系統工程與電子技術，2013，35(3)：580～585.

[17] Gao S S, Hu G G, Zhong Y M. Windowing and Random Weighting-based Adaptive Unscented Kalman Filter[J].International Journal of Adaptive Control and Signal Processing,2014，29(2)：201～223.

[18] 蔣宏，宋龍，任章.非全測狀態下的機動目標跟蹤[J].系統工程與電子技術，2007,29(2)：197～200.

[19] 柯晶,錢積新.加性復合有色噪聲干擾下的強跟蹤濾波器[J].儀器儀表學報,2003,24(1):19～22.

[20] 房建成,萬德鈞,吳秋平.GPS動態定位的強跟蹤卡爾曼濾波研究[J].東南大學學報(自然科學版),1997,(2):60～66.

[21] 胡高歌,劉逸涵,高社生,等.改進的強跟蹤UKF算法及其在INS/GPS組合導航中的應用[J].中國慣性技術學報,2014,22(5)：634～639.

OverviewofEstimationAlgorithmforTwoUKFFilters

JIA Wen-zhe, WANG Jian-ping

(FacultyofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology,Kunming650504,China)

Through reviewing Kalman filter’s development, the sampling strategies for standard UKF and unscented transform were proposed.Through analyzing standard UKF, the square root UKF and the strong tracking UKF were improved and their corresponding algorithm was presented and UKF algorithm was summarized and reviewed.

UKF, sampling strategy, square root UKF, strong tracking UKF

TP14

A

1000-3932(2016)10-1011-04

2015-12-17(修改稿)

國家自然科學基金項目(61364008)；云南省應用基礎研究重點項目(2014FA029)；云南省教育廳重點基金項目(2013Z127)；昆明理工大學復雜工業控制學科方向團隊建設計劃項目