基于線性化模型的汽油調合過程動態優化
吳 威 戴連奎
(浙江大學工業控制技術國家重點實驗室,杭州 310027)
基于線性化模型的汽油調合過程動態優化
吳 威 戴連奎
(浙江大學工業控制技術國家重點實驗室,杭州 310027)
針對現有的調合模型復雜且參數難以獲取、優化算法繁瑣的缺陷,引入動態優化思想,將汽油調合優化過程分解成若干個短周期,對每一段短周期內汽油辛烷值等質量指標進行線性化處理,建立了一種汽油調合線性動態模型。結合實際工藝背景,對汽油調合優化目標函數和約束條件進行了數學描述,并將其轉換成簡單的線性規劃問題。與此同時,運用在線分析技術獲取調合過程當前工況下的調合汽油和組分油的質量指標,用于實時更新優化模型。仿真結果表明:基于線性化模型的汽油調合過程動態優化方案在在線分析儀精度達到要求的情況下,能很快、精確地跟蹤質量指標目標設定值,實現調合汽油質量指標的卡邊控制,并提高調合利潤。
汽油調合 實時優化 在線分析
隨著國家對車用汽油質量指標的要求越來越重視,除了辛烷值之外,對烯烴、芳烴及氧含量等都有嚴格的限制。汽油調合優化是利用多種組分汽油,按照適當的比例進行混合,在滿足車用汽油指標的條件下,調合出利潤最大的高品質汽油[1]。近年來,國內外眾多科研機構對汽油調合優化進行了深入的研究,建立了多種汽油調合辛烷值模型,并提出了多種優化求解算法。
對于汽油調合辛烷值模型,學者們已經提出了一些典型的建模方法。Zahed A H等基于實驗方法來預測調合汽油辛烷值[2],此方法需要已知各組分油的辛烷值、流量,模型中參數需要通過實驗數據進行回歸分析得到;李信等提出一種基于最小二乘支持向量機的方法對辛烷值進行預測建模[3];張希發等通過確定汽油辛烷值與烴族組成的定量關系來建立汽油調合模型[4]。對于調合優化問題,黃彩鳳等采用機會約束規劃進行求解[5],將優化問題中帶不確定參數的約束以概率形式加以表示,從而將隨機規劃問題轉化為相應的確定性規劃問題進行求解。袁奇等將全局群搜索優化算法運用到汽油調合上[6],提高了優化過程的收斂速度和性能。Mendez C A等將汽油調合混合整數非線性規劃問題轉化為一系列的混合整數線性規劃問題進行求解[7],以獲得最優的組分油流量。
筆者將汽油調合過程分解為若干個短周期,在每一個短周期內用線性化模型來近似描述調合汽油辛烷值等質量指標,并基于該線性化模型,采用常規的線性規劃算法以獲得調合過程中的最優組分油流量比。在此基礎上,針對汽油調合優化過程進行了較為深入的仿真實驗研究,并就在線分析儀測量誤差及原料價格發生變動等情況對動態優化過程的影響進行了分析。
1 汽油管道自動調合系統結構
某煉油廠汽油管道調合工藝采用5種組分油,分別為催化汽油、重整汽油、MTBE、石腦油和非芳,將它們按照一定的比例混合,可同時生產出符合國IV標準的93#、97#汽油或者國V標準的92#、95#汽油。組分油中的催化汽油、重整汽油和非芳均直接來自于各自相應的生產裝置,無中間緩沖罐,同時流經一個管道,其進料全部參與調合。為方便對調合過程進行描述,以93#汽油為例,將此管道輸送混合油等價為催化汽油,由此簡化后的汽油調合系統如圖1所示。其中催化汽油為主組分油,低辛烷值的石腦油和高辛烷值的MTBE作為輔助組分油,其進料流量r2和r3按照一定的比例參與調合。將3種組分油同時輸入管道混合器,最終目標是在生產出質量指標合格的93#汽油的前提下,使調合利潤達到最大化。流量的調節回路由流量變送器FT、流量控制器FC和控制閥組成,流量控制器設定值由比值控制器提供。比值控制器的輸入為石腦油、MTBE與催化汽油流量比值的最優值u2*、u3*,輸出為石腦油流量設定值(F2sp)和MTBE流量設定值(F3sp)。優化控制器依據當前產品質量與卡邊值之間的偏差,實時計算最優流量比u2*和u3*,以生產出質量合格的調合汽油,并使調合利潤最大化。
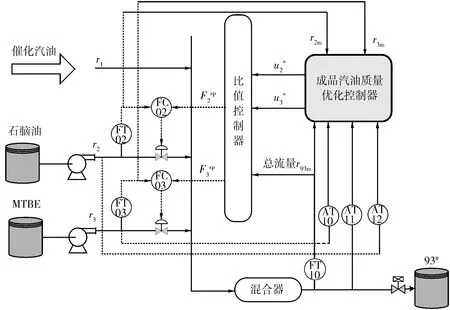
圖1 汽油管道自動調合系統
2 汽油在線調合優化問題的數學描述
汽油調合過程的優化目標是在滿足調合汽油各項質量指標要求的前提下,使調合利潤最大化,其目標函數可表示為:
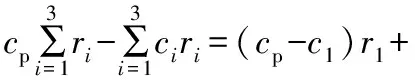
(cp-c2)r2+(cp-c3)r3
(1)
式中c1、c2和c3——催化汽油、石腦油和MTBE的成本價格,元/噸;
cp——成品汽油的市場銷售價格,元/噸;
r1、r2和r3——催化汽油、石腦油和MTBE的流量,m3/h。
由于c1、c2、c3和cp短期內保持不變,單位催化汽油所得的最大調合利潤J為:
maxJ=(cp-c2)u2+(cp-c3)u3
(2)
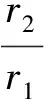
筆者假設催化汽油和石腦油的氧含量為0,MTBE中的芳烴含量為0。因而,質量指標約束可表示為:
y1=f1(u2,u3,x11,x12,x13)≥y1min
(3)
y2=f2(u2,u3,x21,x22)≤y2max
(4)
y3=f3(u2,u3,x33)≤y3max
(5)
其中,x11、x12、x13分別為催化汽油、石腦油和MTBE的辛烷值;x21、x22分別為催化汽油、石腦油的芳烴含量,%;x33為MTBE的氧含量,%;y1、y1min分別為調合汽油的辛烷值及其目標控制下限;y2、y2max分別為調合汽油的芳烴含量及其目標含量的上限,%;y3、y3max分別為調合汽油的氧含量及其目標含量的上限,%。
流量比值和流量比值變化量約束可表示為:
0≤u2≤u2max,0≤u3≤u3max
(6)
-Δu2max≤Δu2≤Δu2max,-Δu3max≤Δu3≤Δu3max
(7)
其中,u2max為石腦油與催化汽油流量比值控制上限;u3max為MTBE與催化汽油流量比值控制上限;Δu2max、Δu3max分別為石腦油、MTBE與催化汽油流量比值變化量上限。
3 調合模型的建立和問題求解
為了求解上述優化問題,需先建立調合汽油3種質量指標與組分油的質量指標和流量比值之間所對應的函數關系。
3.1調合模型的建立
調合汽油的芳烴含量和氧含量與組分油的質量指標和流量比值之間滿足線性可加,即:
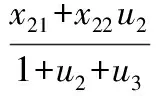
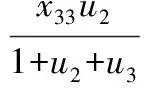
(8)
辛烷值的調合具有非線性效應,預測調合辛烷值的模型主要有Ethyl-70模型、交互模型及神經網絡模型等。其中交互模型[8]是很早就由Morris W E等提出且之后不斷進行改進的經典模型,其曲線如圖2所示。
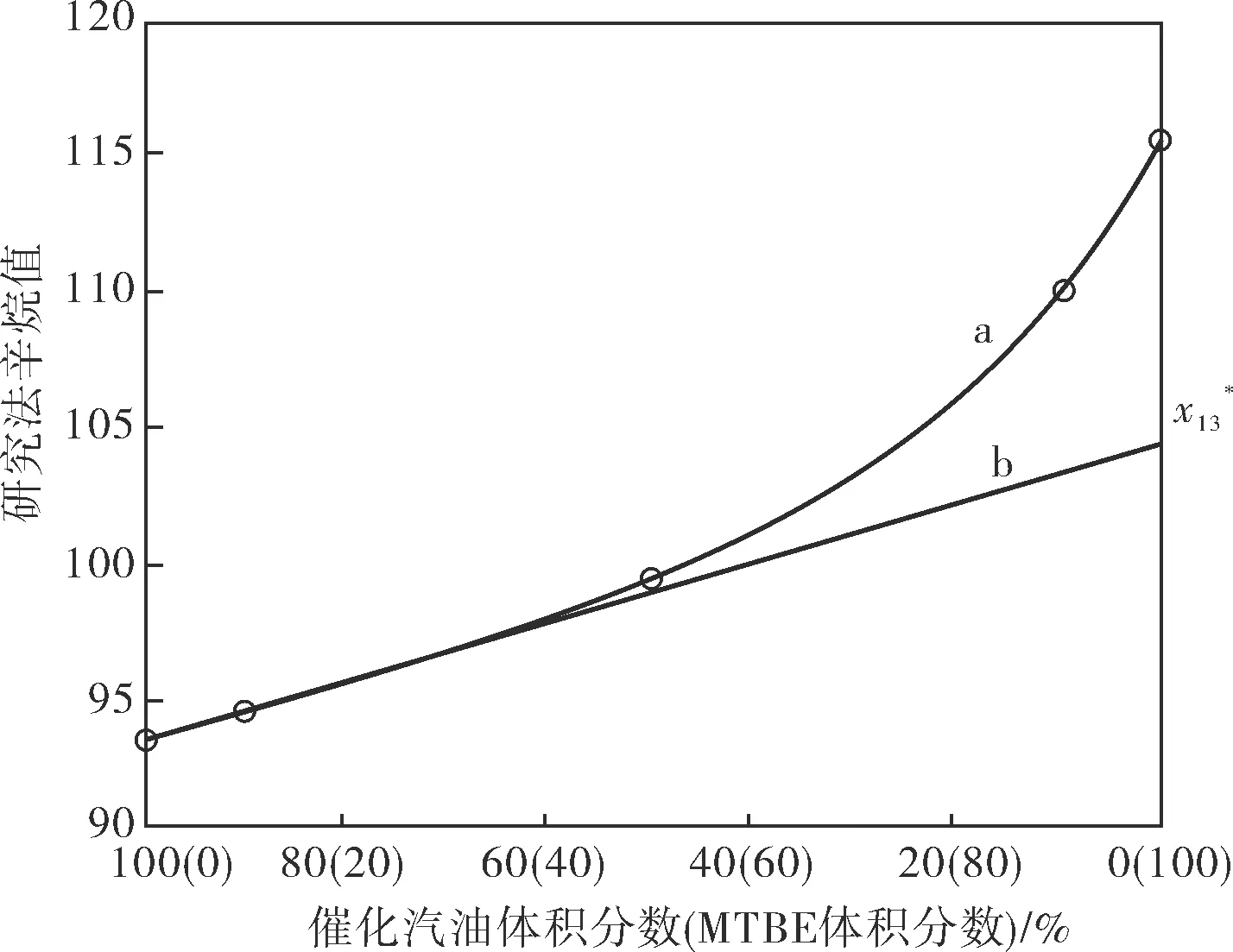
圖2 催化汽油和MTBE相互混合得到的研究法辛烷值曲線
因為在汽油調合過程中,催化汽油為主組分油(70%以上),由圖2直線b可近似得到調合汽油辛烷值:
y1=x11z1+x13*z3
(9)
把上述情況推廣應用到3種組分油的混合過程中,同理可得調合汽油的辛烷值:
y1=x11z1+x12*z2+x13*z3
(10)
也即:
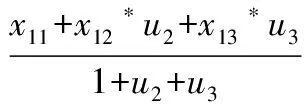
(11)
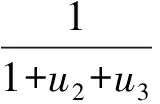
3.2問題求解
通過在線分析儀可實時檢測出該時刻調合汽油的辛烷值、芳烴含量和氧含量yim(k)(i=1,2,3),相互間滿足以下關系:
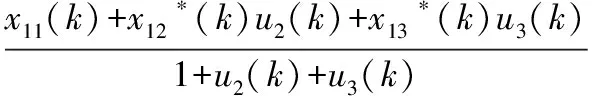
(12)
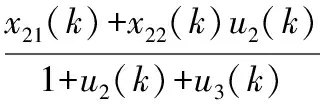
(13)
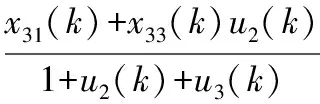
(14)
若在下一時刻ui(k)(i=2,3)變化為ui(k+1),假設各組分油的質量指標僅在一定范圍內緩慢波動,則有:
ui(k+1)=ui(k)+Δui,i=2,3
(15)
以辛烷值為例,k+1時刻調合汽油的各項質量指標y1(k+1)可近似為:
y1(k+1)=
(16)
在k+1時刻,調合汽油質量指標應滿足約束,可得:
y1(k+1)≥y1min
(17)
結合式(12)、(15)和(16)可得:
(y1min-x12*(k))Δu2+(y1min-x13*(k))Δu3≤
(y1m(k)-y1min)(1+u2(k)+u3(k))
(18)
同理,對芳烴含量和氧含量的約束條件可轉化為:
(x22(k)-y2max)Δu2-y2maxΔu3≤(y2max-y3m(k))(1+
u2(k)+u3(k))
(19)
-y3maxΔu2+(x33(k)-y3max)Δu3≤(y3max-y3m(k))×
(1+u2(k)+u3(k))
(20)
由式(17)~(19)可知,為求解上述約束條件,除調合汽油外,還需要利用在線分析儀對石腦油與MTBE的質量指標進行實時檢測,以計算下一周期調合汽油的質量指標。
將上述各式化簡后,短周期內的汽油調合優化問題可近似為:
maxΔJ=J(k+1)-J(k)
=(cp-c2)Δu2+(cp-c3)Δu3
(21)
4 仿真研究
通過Matlab軟件中的Simulink平臺搭建汽油調合優化仿真模型,仿真結構框圖如圖3所示。
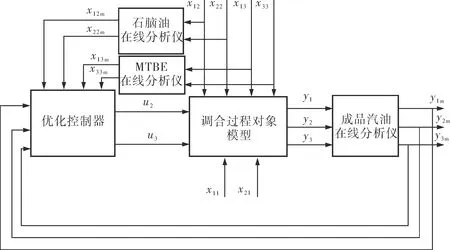
圖3 汽油調合優化仿真結構框圖
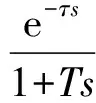
4.1動態優化過程實驗
對于單位催化汽油進料,假設初始的石腦油流量和MTBE流量均為0。設催化汽油、石腦油和MTBE研究法辛烷值的初始值分別為92、65和115,初始芳烴含量分別為30%、10%和0%,初始氧含量分別為0%、0%和18%。研究法辛烷值的目標設定值為93.2,芳烴含量不大于40%,氧含量不大于2.7%。另外,假設93#成品油的價格為每噸8 000元,催化汽油的價格為每噸7 300元,石腦油的價格為每噸7 000元,MTBE的價格為每噸8 300元。動態環節中慣性時間常數T=2min,滯后時間τ=5min。
動態優化過程如圖4所示,其中圖4b為石腦油流量比值的變化曲線,圖4c為MTBE的流量比值變化曲線,所對應的單位催化汽油的調合利潤變化曲線如圖4d所示。
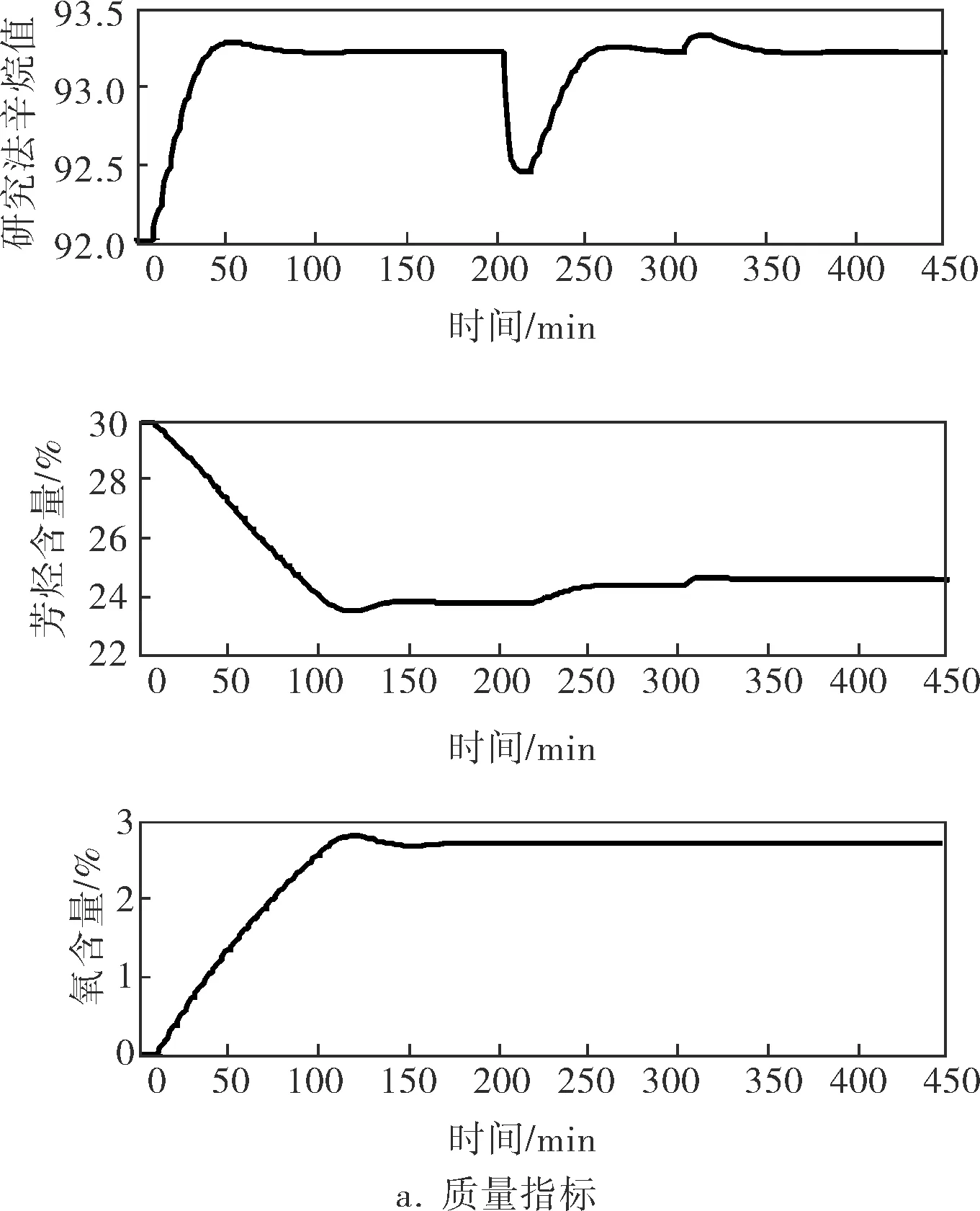
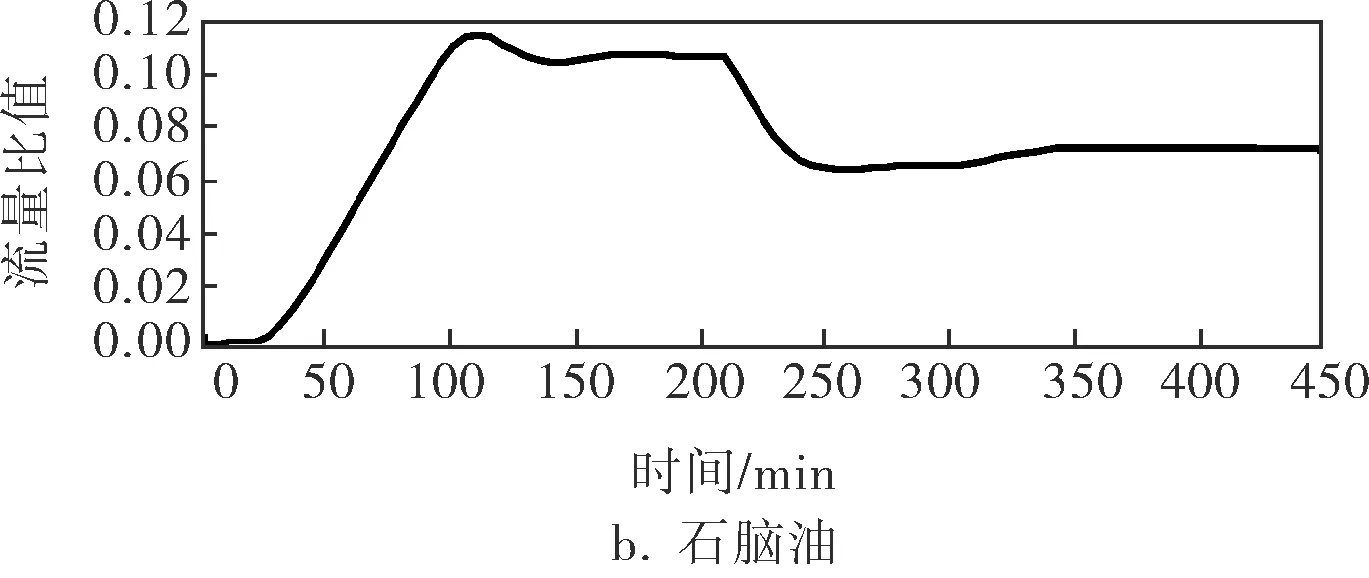
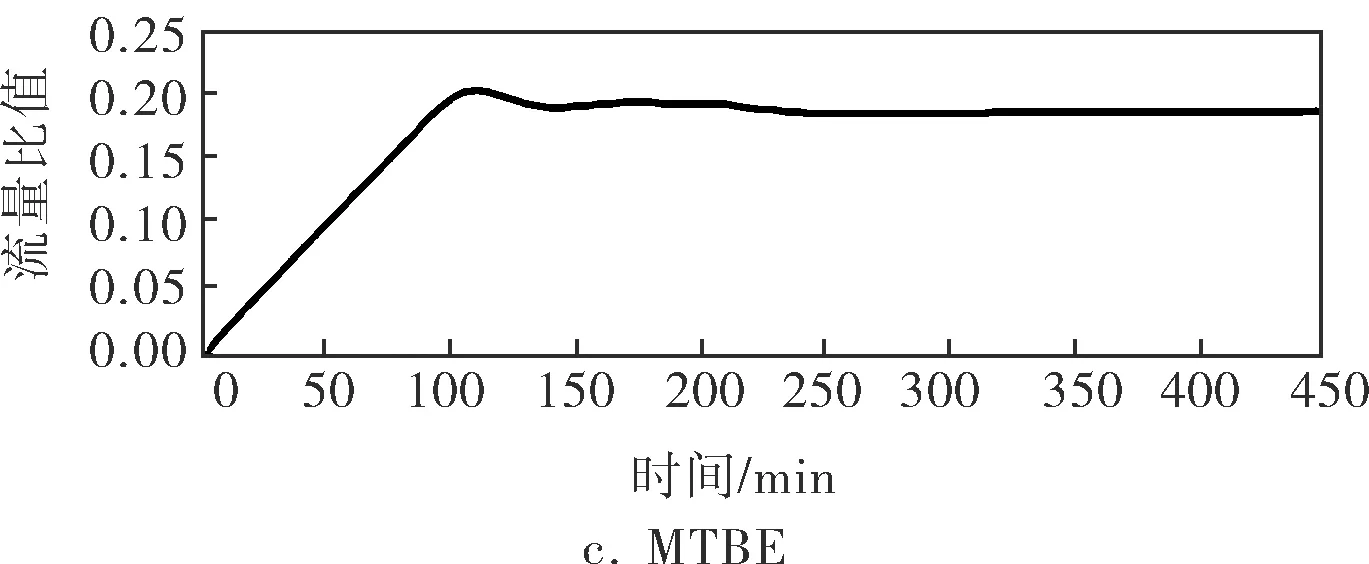
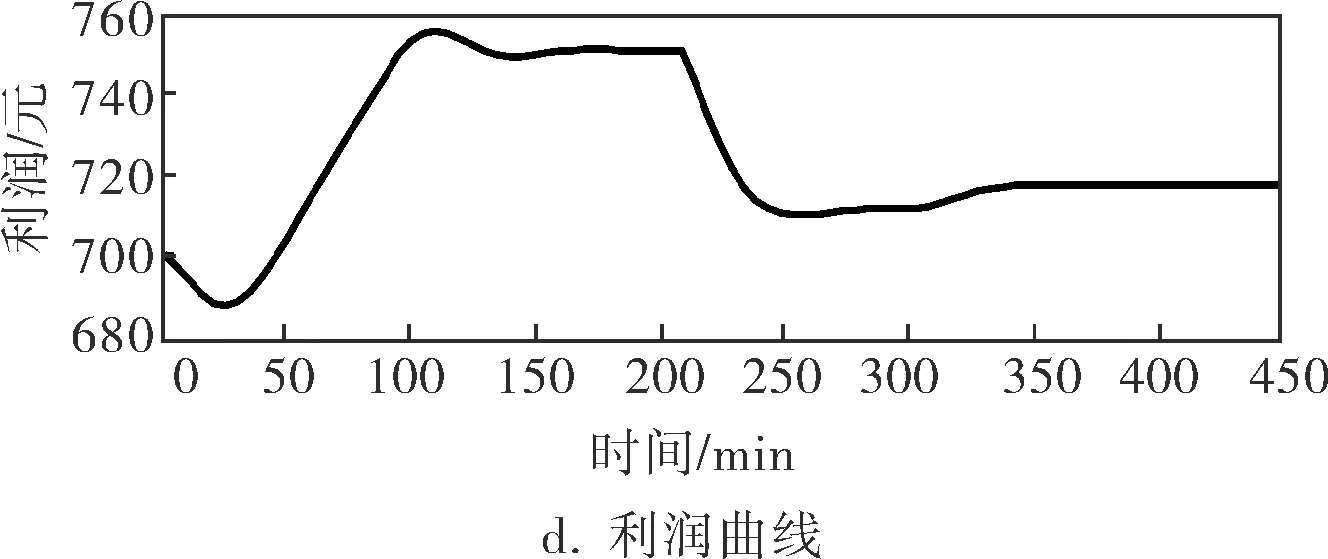
圖4 動態優化過程調合汽油質量指標、流量比值和利潤曲線
在0~200min時間段,3種組分油質量指標均無變化。初始狀態下,調合汽油的辛烷值為92.0,低于設定值,因此高辛烷值MTBE的加入比率應多于石腦油,又受到調合汽油氧含量的限制,MTBE的加入比率應該適量。在200min處,不可測的催化汽油質量指標發生了階躍變化,其辛烷值由92.0變化到91.0,此時調合汽油的對應辛烷值下降。為使辛烷值回到設定值,系統自動減少石腦油的加入量,同時,為了避免氧含量超標,MTBE的加入量也隨之下降。在300min處為石腦油的辛烷值由65階躍變化到67,其芳烴含量由10%階躍變化到15%。
4.2在線分析儀表測量誤差對優化結果的影響
在線分析儀監控整個調合過程成品油的辛烷值、芳烴含量及氧含量等質量指標的變化,將所測的質量指標作為反饋輸入至優化控制器,從而實現組分流量比值的在線調整。以辛烷值為例,若在線分析儀存在測量誤差,比實際值偏大0.1個辛烷值。重復4.1節的實驗,可得到調合汽油辛烷值動態優化曲線如圖5實線所示。可以看出,動態過程穩定后的實際辛烷值比設定值偏小0.1,可見結合在線分析技術的汽油調合優化對分析儀表的精度有較高的要求。
4.3原料市場價格變動對動態優化過程的影響
假設在下一個批次調合前,MTBE的價格從原來的每噸8 300元變為每噸9 300元,按照4.1中的實驗方法重新進行實驗。實驗結果如圖6所示,其中圖6b為石腦油流量比值變化曲線,圖6c為MTBE的流量比值變化曲線,圖6d為所得調合利潤變化曲線。
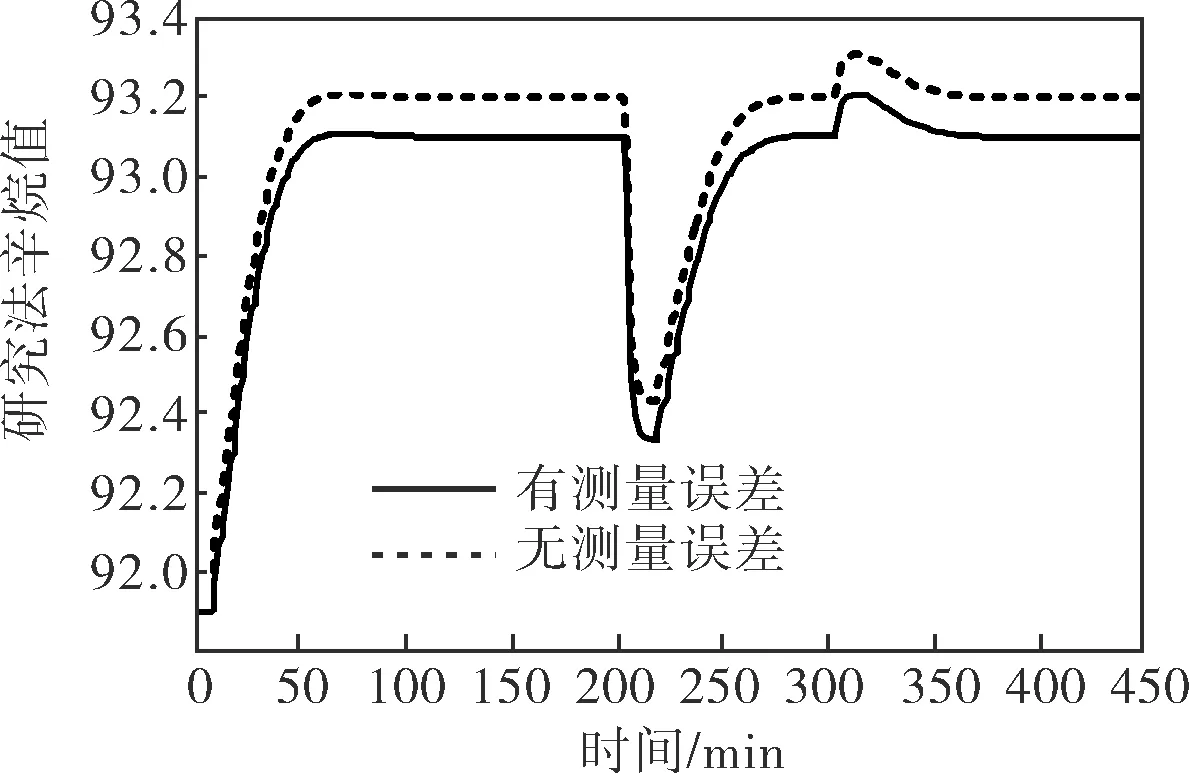
圖5 在線分析儀測得的調合汽油辛烷值動態優化曲線
由圖6可見,當原油的市場價格發生變動時,汽油調合動態優化過程也會相應的發生變化。
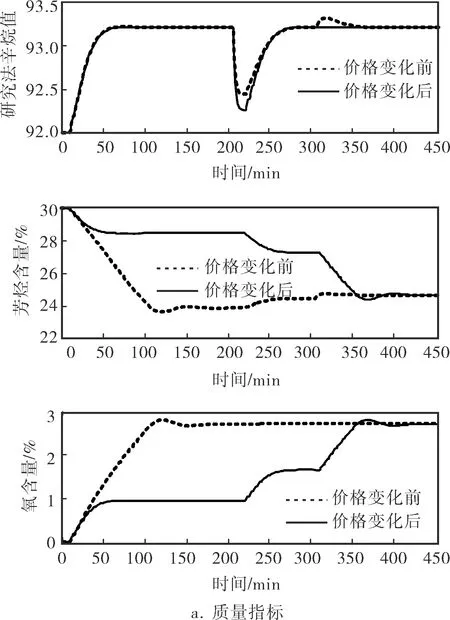
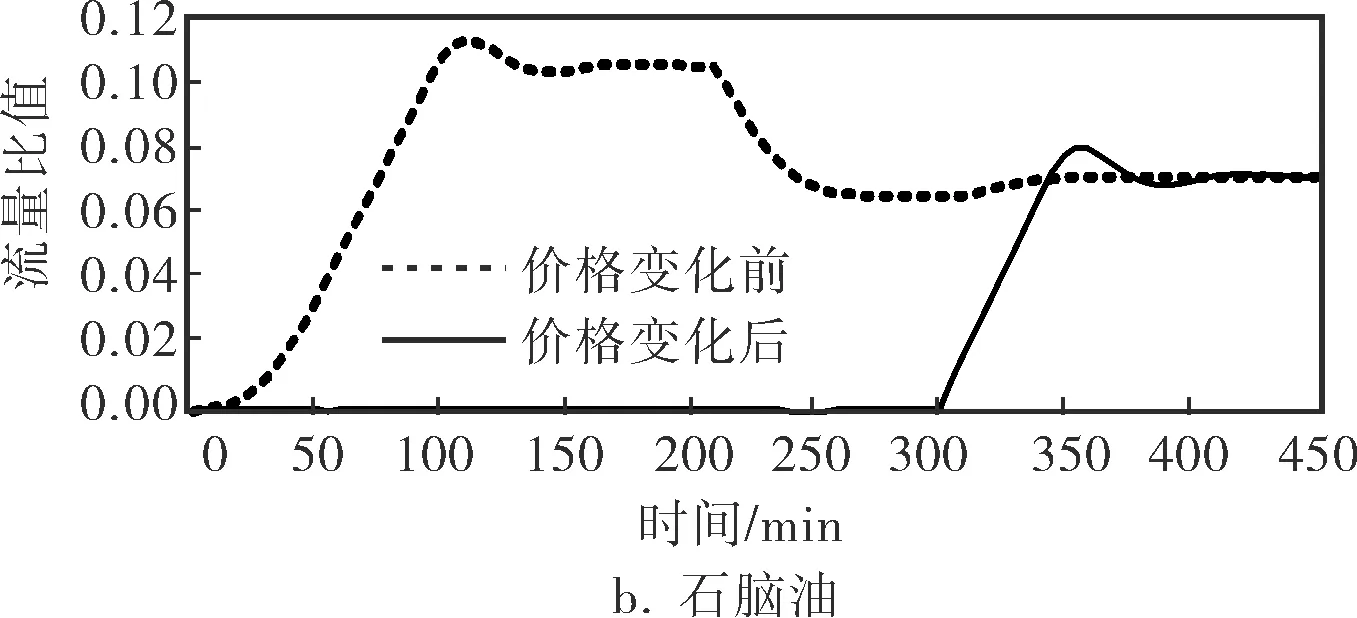
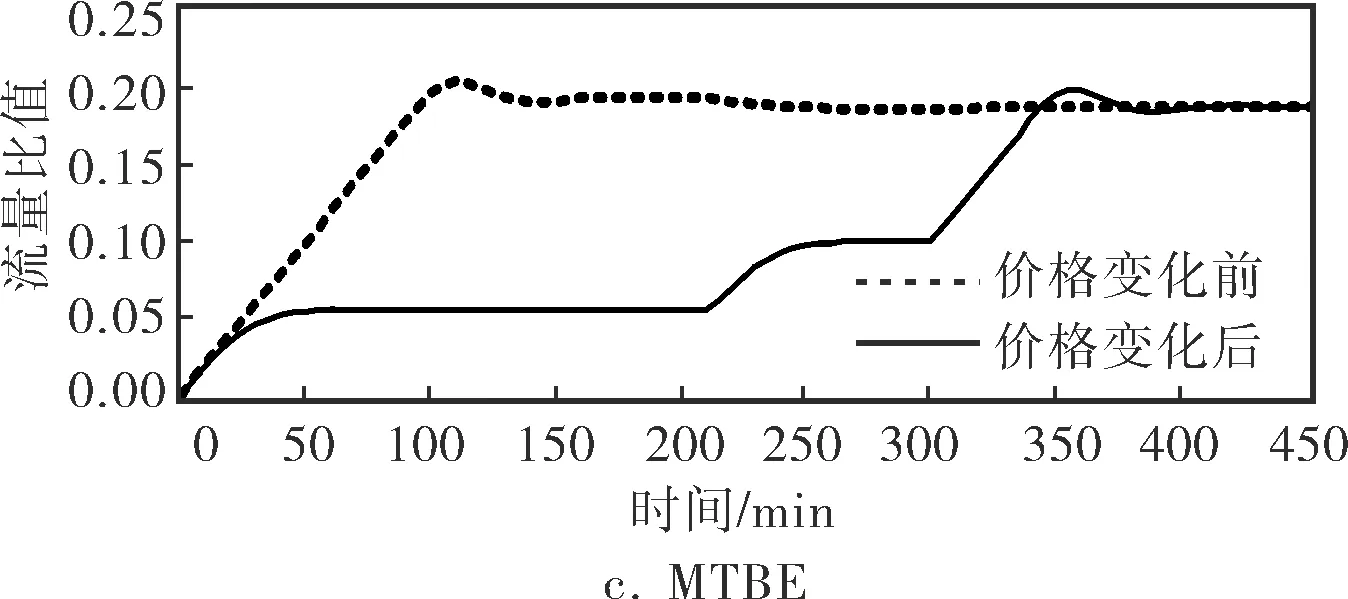
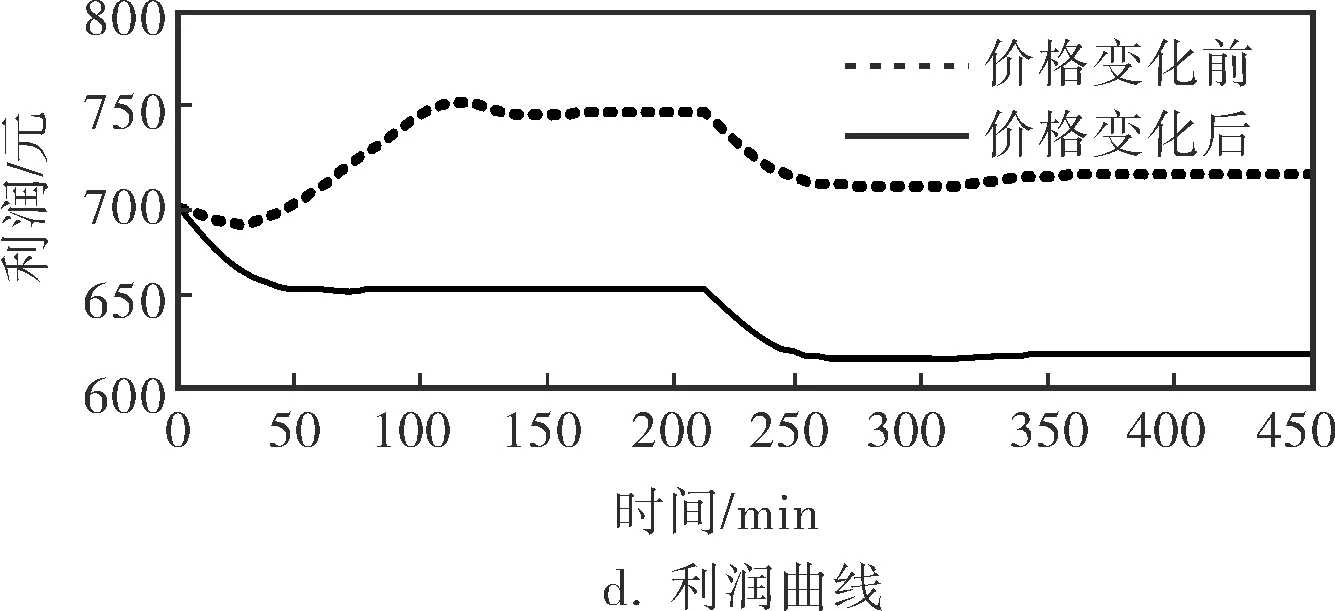
圖6 原料市場價格變動前后動態優化過程質量指標、流量比值和利潤曲線
5 結束語
將汽油調合過程分解成若干個短周期,對每一段短周期內汽油辛烷值等質量指標進行線性化處理,提出了一種新的汽油調合過程動態優化控制方法。仿真實驗結果表明,在分析儀測量精度達到要求的前提下,可以實現組分油流量比值自動調整優化,從而使成品油的質量指標卡邊,并得到最大的調合利潤。即使在組分油的質量指標和原料價格發生變動的情況下,優化控制器仍能夠進行快速有效的優化控制。筆者所采用的模型結構簡單,同時優化算法采用常用的線性規劃,該方法可廣泛應用于煉油生產與調合過程。
[1] Li J,Karimi I A,Sarinivasan R.Recipe Determination and Scheduling of Gasoline Blending Operations[J].AICHE Journal,2010,56(2):441~465.
[2] Zahed A H,Mullah S A,Bashir M D,et al.Predict Octane Number for Gasoline Blends[J].Hydrocarbon Processing,1993,(5):85~87.
[3] 李信,李少遠,黃彩鳳.最小二乘支持向量機在汽油調合建模中的應用研究[J].化工自動化及儀表,2006,33(3):14~16.
[4] 張希發,任連嶺,劉長法,等.基于烴族組成的汽油調合優化模型研究[J].石油煉制與化工,2012,43(6):93~97.
[5] 黃彩鳳,李信,李少遠.基于Ethyl RT-70模型的汽油調合優化[J].控制工程,2007,14(3):256~259.
[6] 袁奇,程輝,鐘偉民,等.全局群搜索優化算法及其在汽油調合中的應用[J].化工學報,2013, 64(12):4427~4433.
[7] Mendez C A,Grossmam I E,Harjunkoski I,et al.A Simultaneous Optimization Approach for Off-line Blending and Scheduling of Oil-refinery Operations[J].Comp Chem Eng,2006,30(4):614~634.
[8] Morris W E,Smith W E,Snee R D.Interaction Blending Equations Enhance Reformulated Gasoline Profitability[J].Oil & Gas Journal,1994,30(3):54~58.
DynamicOptimizationofGasolineBlendingProcessBasedonLinearizedModel
WU Wei, DAI Lian-kui
(StateKeyLaboratoryofIndustrialControlTechnology,ZhejiangUniversity,Hangzhou310027,China)
Considering the fact that existing blending optimization models are complex and it is difficult to obtain model parameters and optimize the algorithm, a dynamic optimization idea was introduced which has gasoline blending scheme divided into several short periods so as to linearly process the octane number during a short term and to establish a linear dynamic model for the gasoline blending. Through considering the actual gasoline blending process, both objective function and constraint conditions were described mathematically and converted to simple linear programming, meanwhile, applying on-line analytical technologies to obtain quality indexes of both blended gasoline and component gasoline in the blending process to update and optimize the model. The simulation results show that this linearized model-based optimization scheme can quickly and accurately track the setting value of quality indexes and to realize the boundary control of gasoline product quality as well as increase the economic benefit.
gasoline blending, real-time optimization, online analysis
TP273
A
1000-3932(2016)03-0252-06
2016-01-05(修改稿)
國家高技術研究發展計劃項目(2012AA10503)

