一種新型初始扭轉Euler-Bernouli梁單元

辛 旭 飛

(國核電力規劃設計研究院，北京 100094)

?

一種新型初始扭轉Euler-Bernouli梁單元

辛 旭 飛

(國核電力規劃設計研究院，北京 100094)

采用有限元理論，借鑒平面Euler梁單元的位移模式，提出了一種2節點8自由度的初始扭轉Euler梁單元，基于該單元的剛度矩陣和質量矩陣，自編有限元程序，求解初始扭轉梁的自振頻率，并通過算例，分析證明了初始扭轉Euler梁單元的合理性和高效性。

初始扭轉Euler梁，單元剛度矩陣，有限元程序

0 引言

近年來涌現出的大量新型空間結構，如網殼、懸索、張拉索—膜結構，充分體現了現代建筑結構富于變換的特點。為滿足建筑造型和工程結構的需要,新型空間結構的設計采用了大量初始扭轉桿件。2008年北京奧運會主體育館“鳥巢”就是這類結構的典型代表，如圖1所示。

初始扭轉構件指構件本身的幾何形態呈現扭轉狀態。由于扭轉角的存在,初始扭轉構件兩個彎曲方向的受力和變形相互耦合，其受力比較復雜。故部分學者[1-3]進行了該梁力學性能的理論研究。

于是，部分學者開始借助有限元技術，用殼單元模擬初始扭轉梁[4,5]。但由于位移模式不準確，結果仍有誤差，而且耗時、耗資。為了彌補殼單元模擬初始扭轉梁的不足，部分學者[6,7]直接開展了該梁的靜力和動力有限單元研究，但考慮因素相對較少。

基于初始扭轉梁研究不足的現狀，本文針對忽略剪切效應的常規初始扭轉梁，采用有限元基本理論，開展了新型初始扭轉Euler-Bernouli梁有限單元的研究。

1 初始扭轉Euler-Bernouli梁單元剛度矩陣和質量矩陣的建立

如圖2所示，初始扭轉梁結構存在兩種坐標系，梁單元整體坐標系(x-y-z)和梁截面局部坐標系(x′-y′-z)。在整體坐標系下定義節點自由度和建立單元剛度矩陣。

單元有2個節點，并且每個節點有4個節點自由度。根據節點自由度，使用插值理論構造初始扭轉梁單元的位移場。

(1)

(2)

其中，w(z)，v(z)分別為y方向，x方向的位移；u1，u2分別為節點1,節點2沿y方向的位移；u3,u4分別為節點1,節點2沿y方向的轉角；u5,u6分別為節點1,節點2沿x方向的位移；u7,u8分別為節點1,節點2沿x方向的轉角。

在式(1)的基礎上，建立初始扭轉梁單元的應變能和動力。

因不考慮剪切應變和軸向變形，扭梁中應變能U僅為兩個方向彎曲引起的應變能：

(3)

其中，l為梁單元長度；E為材料的彈性模量；Ixx，Ixy，Iyy均為初始扭轉梁截面慣性矩。

Ixx，Ixy，Iyy的計算公式為：

(4)

其中，b，h分別為梁截面的寬度和高度；θ為截面扭轉角，θ=c·z+θ0，θ0為坐標原點處截面的初始扭轉角，c為扭率。

初始扭轉梁的動能T包括線位移引起項和轉動慣量項，為：

(5)

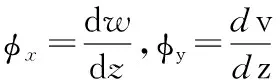
最終扭轉梁的應變能U和動能T的矩陣表達形式為：

(6)

(7)

基于K和M，可以方便地建立初始扭轉梁單元的動力方程，求解出扭轉梁的動力特性。

2 算例驗證

表1 初始扭轉梁本文計算結果與Banerjee[7]所得結果的比較

表2 兩端固定梁自振頻率表 ×103

根據上述初始扭轉梁有限元理論的介紹，本文自編程序計算初始扭轉Euler梁的自振頻率。通過與Banerjee[7]所得結果的對比來說明這種梁單元的有效性和精度。

由表1可見，本文所算結果與Banerjee所算結果基本一致，說明本文所提扭轉梁單元的正確性。由表2可見，對于梁的前四階自振頻率值，從5個、6個單元開始趨于穩定(頻率值變化小于2%)，說明本文所提新型單元具有較高的計算效率，只需要少量單元，就能獲得理想的計算結果。

3 結語

本文基于有限元理論，建立了一種新型的初始扭轉梁單元模型。通過算例分析表明本文所建立的有限元模型不但精度高，而且計算效率高，方便工程應用。

[1] 虞愛民.自然彎扭梁的非線性分析[J].力學季刊，2002，23(2)：275-281.

[2] 虞愛民,易 明.自然彎扭梁廣義翹曲坐標的求解[J].應用數學和力，2004，25(10)：1067-1075.

[3] 陳昌宏，單 建，黃 鶯.初始扭轉矩形梁力學性能研究[J].工業建筑，2009，39(4)：54-57.

[4] 陳春華，舒贛平.具有初始扭轉的箱型截面梁的極限抗彎承載力研究[J].工業建筑，2009，39(S1)：1685-1693.

[5] 陳昌宏，單 建，黃 鶯.初始扭轉軸壓桿彈性彎扭屈曲性能研究[J].工程力學，2009，26(6)：166-171.

[6] 陳昌宏，黃 鶯，單 建.初始扭轉歐拉梁有限元力學模型研究[J].工業建筑，2012，42(5):94-97.

[7] J.R.Banerjee.Free vibration analysis of a twisted beam using the dynamic stiffness method[J].International Journal of Solid and Structure,2001(38)：6703-6722.

On new pre-twisted Euler-Bernouli beam element

Xin Xufei

(StateNuclearElectricPowerPlanningDesignandResearchInstitute,Beijing100094,China)

The paper adopts the finite element theory, points out 2-joint and 8 DOF pre-twisted Euler beam element by referring to the displacement model of the plane Euler beam element, designs the finite element program based on the stiffness and quality matrix of the element, solves the self-vibration frequency of the pre-twisted beam, and through the example, analyzes the pre-twisted Euler beam is reasonable and efficient.

pre-twisted Euler beam, element stiffness matrix, finite element program

1009-6825(2016)20-0035-02

2016-05-13

辛旭飛(1979- )，男，工程師

TU311.4

A