Hierarchical space–time block codes signals classification using higher order cumulants

Ling Qing,Zhng Limin,*,Yn Wenjun,Kong Dongming

aInstitute of Information Fusion,Naval Aeronautical and Astronautical University,Yantai 264001,China

bEquipment of Navy,Taiyuan 030027,China

Hierarchical space–time block codes signals classification using higher order cumulants

Ling Qinga,Zhang Limina,*,Yan Wenjuna,Kong Dongmingb

aInstitute of Information Fusion,Naval Aeronautical and Astronautical University,Yantai 264001,China

bEquipment of Navy,Taiyuan 030027,China

An efficient method for blind classification of space–time block codes(STBCs)based on fourth-order cumulants is proposed for a single receiver antenna.This paper presents a model of

STBCs signals in multiple input single output(MISO)communication systems and applies the characteristics of coding matrices to derive analytical expressions for the fourth-order cumulants to be used as the basis of an algorithm.The fourth-order cumulants at various delay vectors present non-null values that depend on the transmitted STBCs.Tests of nullity are accomplished by hypothesis testing.The proposed algorithm avoids the need for a priori information of modulation scheme,channel coefficients,and noise power.Consequently,it is well suited for non-cooperative scenarios.Simulations show that this method performs well even at low signal-to-noise ratios(SNRs).

1.Introduction

Obtaining signal parameters of the intercepted signals is a key step between signal detection and signal decoding in noncooperative scenarios.Signal parameters include modulation scheme,channel coding information and code parameters.In recent years,the traditional blind classification of signal parameters, including interference identification, signalconfirmation,radio surveillance and spectrum monitoring,has been extended to both military and commercial applications.Array signals can be employed to estimate target signals in multiple input multiple output(MIMO)communication systems.However,a single receiver antenna is favored for many practical applications due to size,power,and cost constraints.Consequently,further work is needed to address the important practical problems of classifying signals with a single receiver antenna.

Space–time block coding is a practical signal design technique aimed at capitalizing on the theoretical information capacity of MIMO channels.1MIMO communication systems accompanied by space–time block codes(STBCs)have been standardized in IEEE 802.16e and IEEE 802.11n,and appear to be ideal technologies for the next generation of wireless communication.Consequently,the blind classification of STBCs is a key research issue in non-cooperative MIMOSTBC communication systems and can be divided into four categories:maximum likelihood,2,3second-order statistics,4–8cyclostationarity-based9–12and fourth-order statistics.13–15Maximum likelihood algorithms employ the maximum likelihood criterion to find optimum solutions.However,their computational complexity is too high for higher order modulation,and they require a priori information,such as channel coefficients,modulation scheme,carrier frequency offset and carrier phase.2,3Second-order statistics is a method based on the space–time correlation of received signals to classify the STBCs in multiple receiver antennas systems.4–8In Refs.9–12,the cyclostationarity properties of received signals are exploited for the classification of STBCs in the context of multiple receiver antennas.The fourth-order statistical method uses the fourth-order statistics of received signals as discriminating signal features to classify the STBCs with a single receiver antenna14,15or to estimate channel coefficients.13However,except for Refs.14,15,most previous research3–15focuses on the context of multiple receiver antennas.Therefore,further work is needed to address the practical problem of classifying the STBCs with a single receiver antenna.In this paper,we propose a STBCs classification algorithm based on fourth-order cumulants with a single receiver antenna over frequency-flat Nakagami-m fading channels.16This algorithm does not require any a priori information of modulation scheme,channel coefficients or noise power.Consequently,it is well suited for non-cooperative scenarios.

Three distinct differences exist between the proposed method and those found in Refs.14,15First,fourth-order cumulants are employed in this paper,however,fourth-order moment(FOM)and the discrete fourier transform(DFT)of the fourth-order lag product(FOLP)are used in the literature.14,15The fourth-order cumulants of zeros-mean Gaussian white noise are equal to zero and the fourth-order moment is not equal to zero.Theoretically,we can ignore the effect of the Gaussian white noise in the derivation of theoretical value of the fourth-order cumulants.This explains why the proposed algorithm performs better than other methods in Refs.14,15at a low SNR.Second,the proposed algorithm can classify general STBCs while those in Ref.14only distinguish Alamouti coding from spatial multiplexing(SM).Moreover,Spatial Multiplexing cannot be categorized into the STBCs.Finally,the fourth-order lag cumulants of STBCs present non-null values that depend on the transmitted STBCs.The FOM-based algorithm employs the likelihood ratio test for decision making.The FOLP-based algorithm detects the peaks or the position of the peaks within the frequency domain of the fourth-order lag product in Refs.14,15

The rest of this paper is organized as follows:Section 2–signal model and assumptions;Section 3–the derivation of the fourth-order cumulants of STBCs;Section 4–the proposed STBCs classification algorithm;Section 5–simulation results;Section 6–conclusions.

2.Signal model and assumptions

Let us consider a wireless communication system composed of a single receiver antenna and Nttransmit antennas.We assume the symbols that belong to the same complex linear modulation are independent and identically distributed(i.i.d)random variables.For quadrature phase shift keying(QPSK)constellation,the real and imaginary parts of the transmitted symbols are also i.i.d. That is to say, E(|x|2)=1 and

The N transmitted symbols can be divided into blocks with length of Ns.Each block of Nsmodulated symbols is encoded to generate Ntparallel signal sequences of length L.The kth block of Nstransmitted complex symbols is denoted by

(1)For SM,a block of Ns=Ntsymbols is transmitted through Ntantennas in a single time period(L=1).The corresponding coding matrix can be given as

(2)For Alamouti coding(Al),a block of Ns=2 symbols is transmitted through 2 antennas in two consecutive time periods(L=2).Alamouti coding is an orthogonal STBC(OSTBC).The corresponding coding matrix can be given as:17

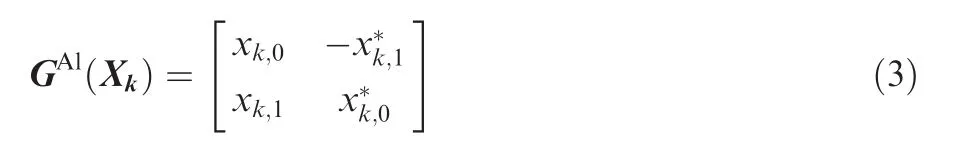
where*represents complex conjugate.

(3)For OSTBC-3/4 coding(ST3),a block of Ns=3 symbols is transmitted through 3 antennas in four consecutive time periods(L=4).The OSTBC-3/4 coding is also an orthogonal STBC.The corresponding coding matrix can be given as:1

(4)For OSTBC-1/2 coding(ST4),a block of Ns=4 symbols is transmitted through 3 antennas in eight consecutive time periods(L=8).The OSTBC-1/2 coding is also an orthogonal STBC.The corresponding coding matrix can be given as:18

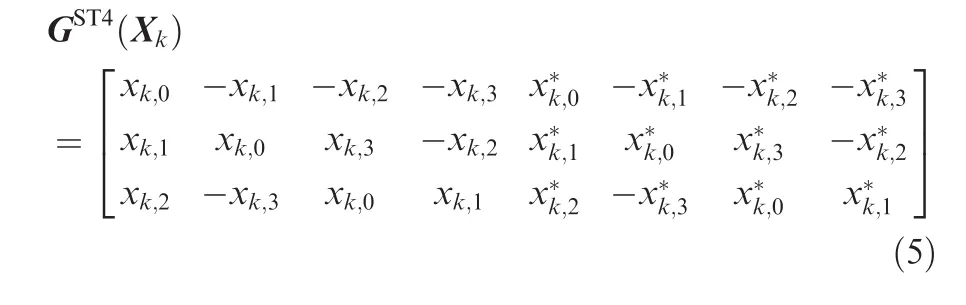
Let us consider a receiver with a single antenna.The length and start of STBCs are unknown at the receiver side in a noncooperative scenario.The first received column is expressed as r(0),so the(k+1)th intercepted column rλ(k)can be denoted as

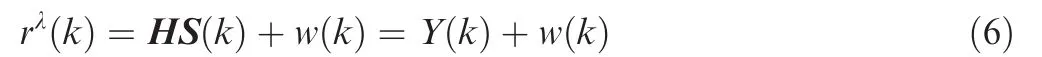
In this paper,we resort to using fourth-order cumulants to blindly classify the proposed STBCs above from K received columns when a single receiver antenna is available.More details are in the next section.

3.The fourth-order cumulants of STBCs

In this section,the expression of fourth-order cumulants is deduced in order to discover the characteristic parameters that can blindly classify STBCs in a non-cooperative scenario.

3.1.Principles

Forthecomplex-valuestationary random process r(k),second-order moments can be defined in two different ways:

Similarly,fourth-order cumulants can be defined in three ways:

where,the statistics in Eqs.(7)and(8)are the zeroth lags of the correlations and fourth-order cumulants of r(k),For zeromean w,x,y,and z,the fourth-order cumulants can be defined as

If random variable xiand yiare statistically independent,the cumulants have the characteristics of half-invariance,so

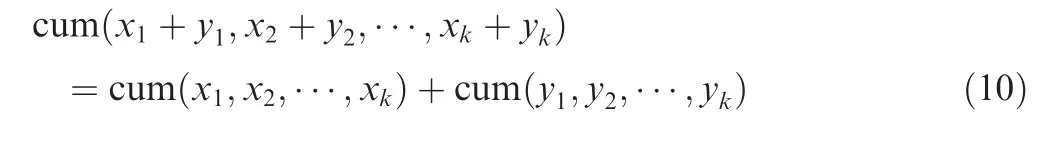
3.2.The derivation of the fourth-order cumulants for STBCs

Eqs.(6)and(10)can be deduced as

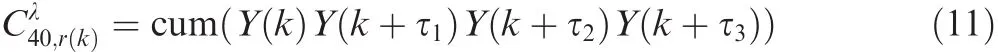
In Refs.19,20,the fourth order cumulants of zeros-mean Gaussian white noise are equal to zero,but the fourth order moments are not equal to zero.Therefore,we choose fourth order cumulants as a tool to blindly classify the STBCs.Eq.(11)can be simplified as

where τ1=0 and τ2= τ3∈ {1,2,5}.

Therefore,the fourth-order cumulants of ST4 at a delayvector[0,0,1,1]can be expressed as

where hirepresents the channel coefficient between the itransmit antenna and receive antenna.

The fourth-order cumulants of ST4 at a delay-vector[0,0,2,2]can be expressed as

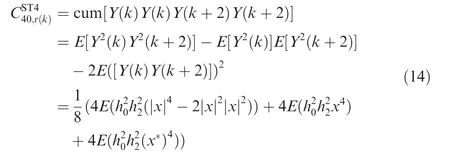
The fourth-order cumulants of ST4 at a delay-vector[0,0,5,5]can be expressed as

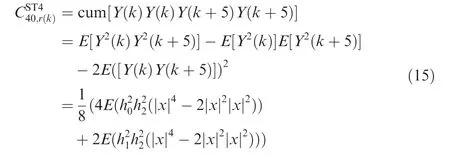
The fourth-order cumulants of SM,Al and ST3 at different delay-vectors can be obtained in similar ways.

For SM,the transmitted symbols are independent in different time slots.Therefore,the fourth-order cumulants of SM are equal to zero at different delay-vectors.

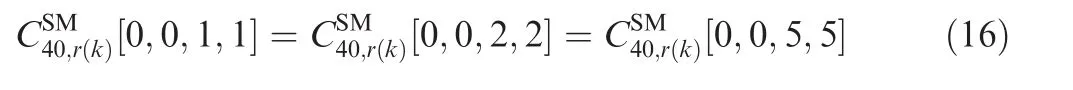
The fourth-order cumulants of Al at different delay-vectors can be deduced as follows:

(1)The fourth-order cumulants of Al at a delay-vector[0,0,1,1]are expressed as

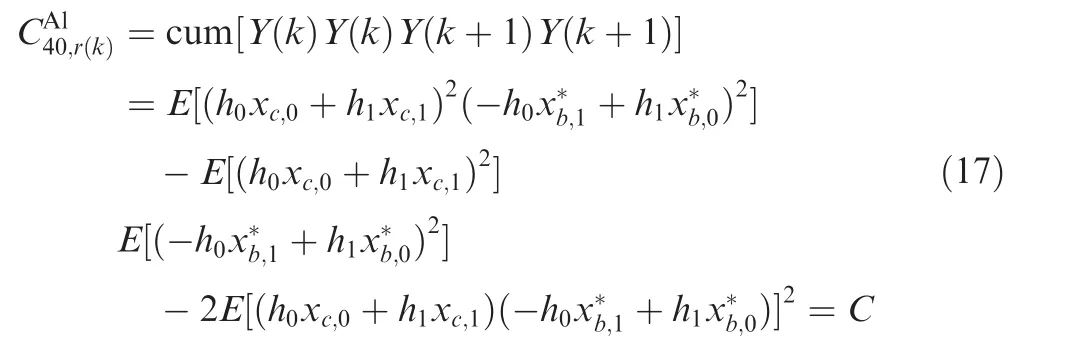
where xc,0represents the zeroth transmit symbol in the cth coding matrix.If c≠b,it represents symbol xc,0and xb,0are not in the same coding matrix.If c=b,C can be expresses as

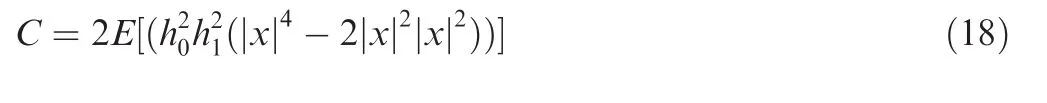
Else

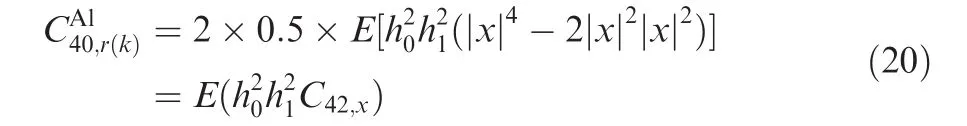
(2)As the length of the code matrix is equal to 2,the transmitted symbols in a different code matrix are independent.The fourth-order cumulants of Al are equal to zero at delay-vectors[0,0,2,2]and[0,0,5,5].

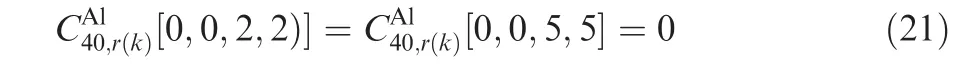
The fourth-order cumulants of ST3 at different delayvectors can be deduced as follows:

(1)The fourth-order cumulants of ST3 at a delay-vector[0,0,1,1]are expressed as

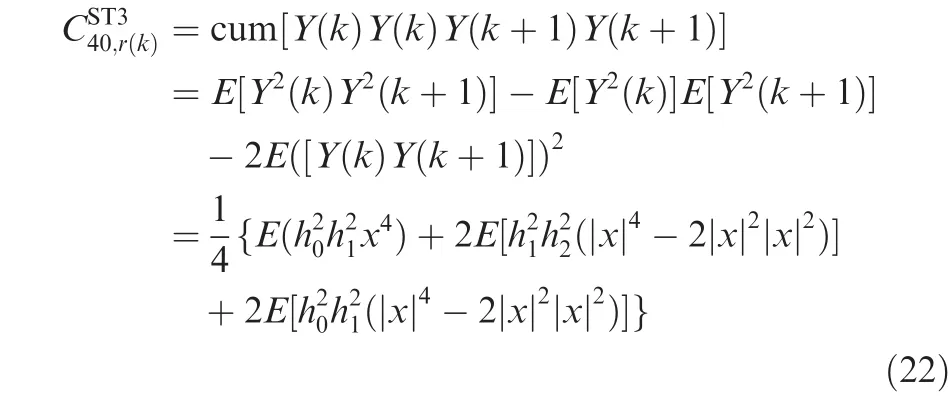
(2)The fourth-order cumulants of ST3 at a delay-vector[0,0,2,2]are expressed as

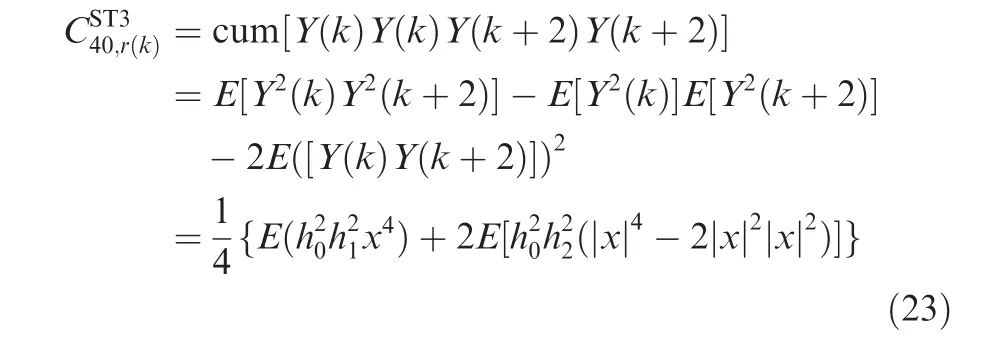
(3)As the length of the code matrix is equal to 4,the fourthorder cumulants of ST3 at a delay-vector[0,0,5,5]are equal to zero.

Examples of moments and cumulants corresponding to different signal constellations are provided in Table 1.In Table 1,PSK refers to phase shift keying,QAM refers to quadrature amplitude modulation,and QPSK refers to quad.

Table 1 Moments and cumulants values for various signal constellations.

The conclusion in Section 3 can be reached that the fourthorder cumulants at different time delays-vectors present nonnull values that depend on the transmitted STBCs.For QPSK modulation,the theoretical values of the fourth-order cumulants for SM,Al,ST3 and ST4 are provided in Table 2.

4.Blind classification of STBCs by decision tree and hypothesis testing

In this section,we propose a classifier for blind recognition of 4 linear STBCs,which are introduced above.The automatic classification of these STBCs is accomplished by using a decision tree.

4.1.The estimated values of fourth-order cumulants

In the practical applications of signal processing,the fourthorder cumulants can be estimated from the limited length received signals. Given the observed data r(k),k=1,2,...,K,the estimation of the fourth-order cumulants can be expressed as

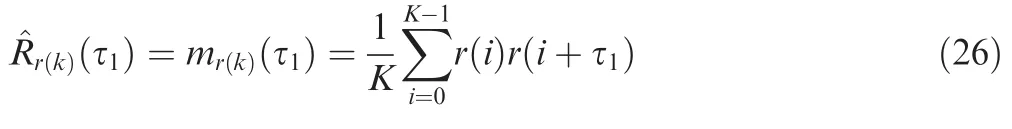
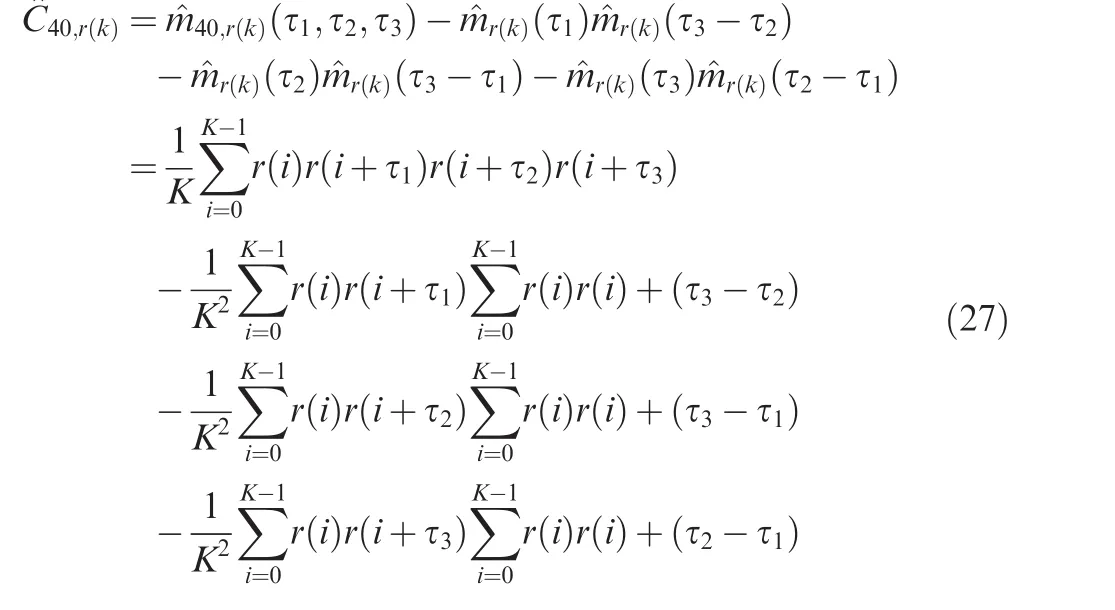
Table 2 Theoretical values of the fourth-order cumulants C40,r(k)at different delay vectors(QPSK modulation).

4.2.Decision tree

From transmission,the theoretical values of fourth-order cumulants are obtained due to the derivation in Section 3.For the 4 STBCs under consideration,the theoretical values of fourth-order cumulants are reported on Table 2.By analyzing Table 2,we propose a new method to blindly classify the STBCs with the decision tree in Fig.1.The ST4 is recognized by the non-null value of fourth-order cumulants at delayvector[0,0,5,5].The presence of the ST3 is then detected from the non-null value of the fourth-order cumulants at delayvector[0,0,2,2].Subsequently,the fourth-order cumulants at delay-vector[0,0,1,1]are used to discriminate Al from SM.At each node of the tree,the nullity of^C40,r(k)is tested.In an experiment,^C40,r(k)can be estimated and the test of nullity accomplished by a hypothesis testing.

4.3.Detection of null values using hypothesis testing

From the data in Table 2,we propose a new method to blindly classify the STBCs by detecting the non-null value of the fourth-order cumulants at different delay vectors.The detection of the non-null values can be performed by the following hypothesis testing:

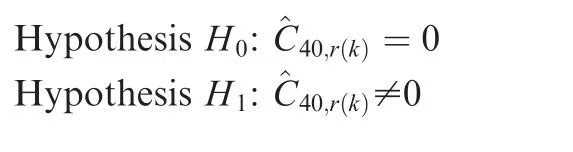
According to central limit theorem,is an asymptotically normal estimator of.The interceptor is composed of a single receiver antenna.Fig.2 presents a histogram offor a wireless communication using ST3 and QPSK modulation.

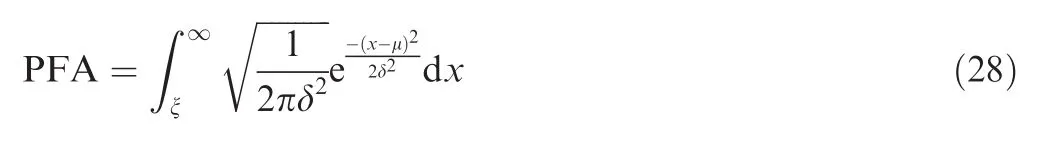
Fig.1 Decision tree for classification of 4 STBCs.

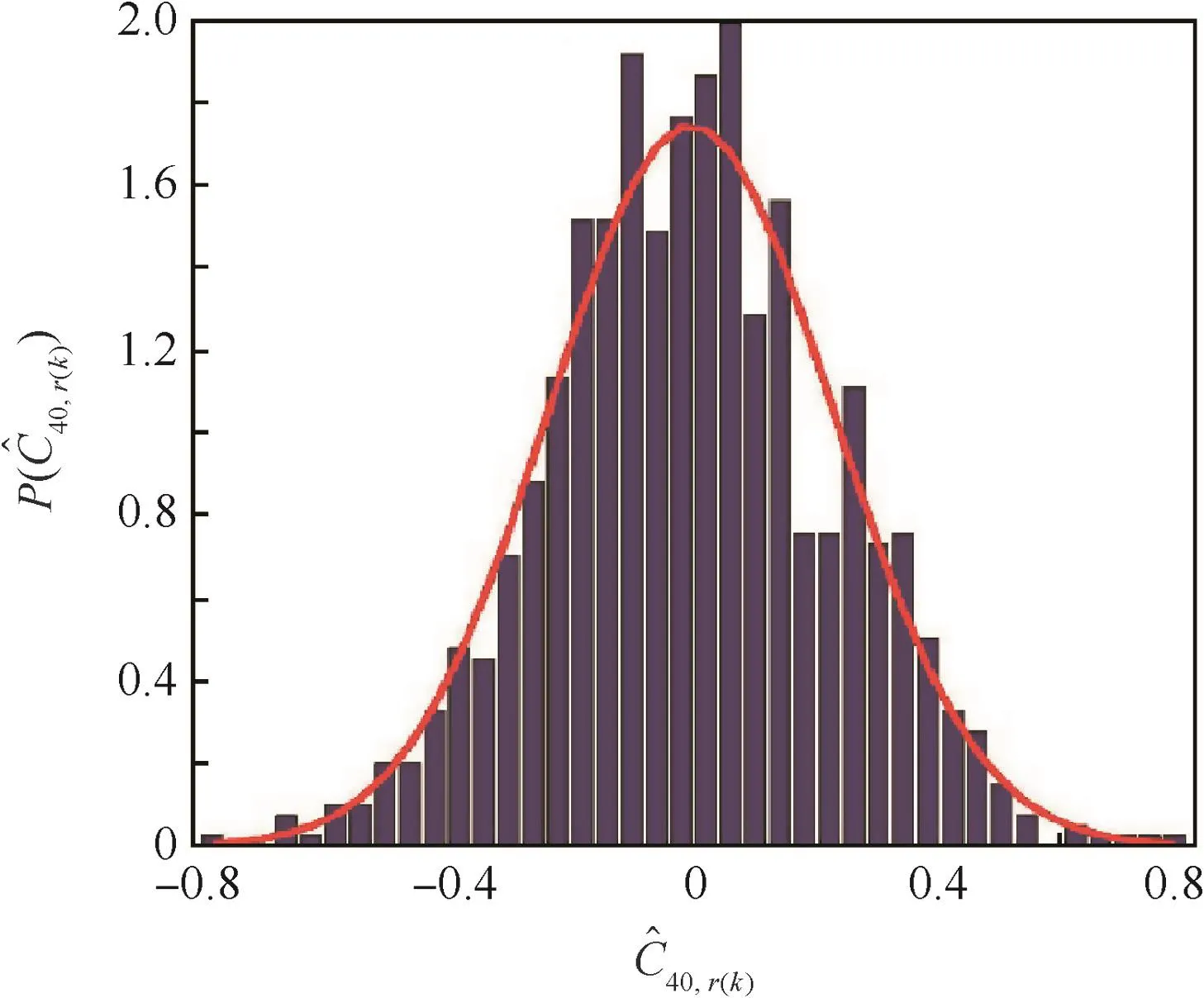
Fig.2 Distribution ofof STBCs at delay-vector[0,0,2,2]at SNR=20 dB.

where,under assumption H0,μ and δ are mean value and variance respectively.Taking the inverse function of Eq.(28)leads to ξ.Hypothesis H0is selected ifotherwise,hypothesis H1is selected.

The average probability of correct classification p(λ|λ),can be expressed as

5.Simulation results

5.1.Simulation setup

1000 Monte Carlo trials were performed to evaluate the performance of the proposed algorithm.SM,Al,ST3 and ST4 were considered in simulations.Unless speci fically indicated,QPSK modulation was used where K=8192 and PFA=10-2.The received signal was affected by additive white Gaussian noise(AWGN)with varianceChannel was set to a frequencyflat Nakagami-m fading channel, with m=3 and E(|hi|2)=1,i=0,1,2,3.SNR was set toTwo performance measures were used: the average probability of correct classification, which was addressed in Eq. (29), and the probability of correct classification p(λ|λ),λ ∈ Ω.

5.2.Performance evaluation

Fig.3 presents the simulation results for the probability of correct classification over the Nakagami-m fading channel for m=3.Note that the probability of correct classification for Al,ST3 and ST4 is dependent on SNRs but not SM.For Al,the probability of correct classification is close to 1 at a SNR equal to-3 dB.For ST3,the probability of correct classification is close to 1 at a SNR equal to 2 dB.For ST4,the probability of correct classification is close to 1 at a SNR equal to 6 dB.Therefore,the proposed algorithm performs well in low SNR scenarios.Al shows better performance than ST3 and ST4 at a low SNR.The fourth-order cumulants of Al,ST3 and SM are subject to Gaussian distribution at delay-vector[0,0,5,5]and their trails have some overlap on the distribution ofof ST4.Therefore,in the hierarchical recognition of STBCs,the recognition of ST4 at first node is disturbed due to the existence of the other STBCs.

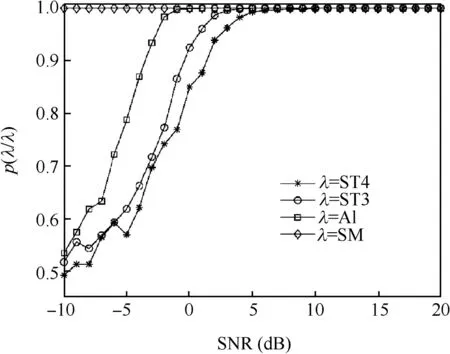
Fig.3 Probability of correct classification p(λ|λ).

5.3.Influence of the number of received samples K

Fig.4 illustrates the classification behavior of a single receiver antenna interceptor with received samples equal to 8192,4096,2048,1024 and 512 respectively.The simulation conditions as follows:the SM,Al,ST3 and ST3 are under consideration and PFA=10-2.In each case,the average probability of correct classification reaches its maximum at a SNR equal to 5 dB.With K=8192,the average probability of correct classification shows better performance at a SNR less than 5 dB.With K=8192,the average probability of correct classification is close to 1 at a SNR equal to 4 dB.The average probability of correct classification is enhanced by a greater number of received samples.This improvement is due to a more accurate estimation of the fourth-order cumulants

5.4.Influence of the probability of false alarm

Fig.5 presents the performance of the proposed algorithm with respect to the probability of false alarm with a single receiver antenna interceptor receiving 2048 samples.In four cases,the average probability of correct classification shows better performance when the probability of false alarm equals 10-2.The analysis is described as follows:is a Gaussian distribution;higher probability of false alarm leads to a lower threshold,therefore,the range of the interval[μ+ξ,2μ-ξ]is enlarged and the performance of classification is enhanced.

Fig.4 Effect of the number of received samples K on Pc.

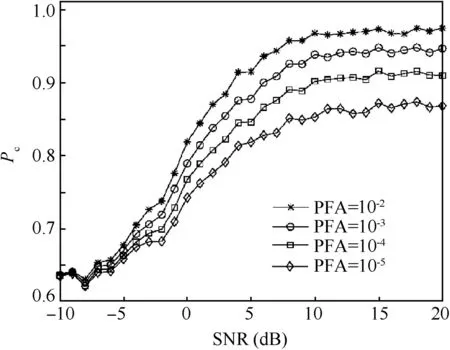
Fig.5 Effect of the probability of false alarm on Pc.

5.5.Influence of the modulation scheme

We have illustrated the behavior of a proposed algorithm for four complex modulation schemes:16-QAM,64-QAM,8-PSK and QPSK.The simulation conditions as follows:the SM,Al,ST3 and ST3 are under consideration,PFA=10-2,K=2048 and m=3.Fig.6 shows performance with respect to modulation scheme.We find that classification performance is dependent on the M-QAM modulation but not M-PSK modulation.The explanation for this phenomenon concerning modulation scheme is described as follows:According to Section 3,the performance of the proposed algorithm is determined by the Euclidean distance between the fourth-order cumulants^C40,r(k)and zero,which improves as the distance increases.The fourth-order cumulants are related to C42,x,which increases as C42,xincreases.C42,xis independent on the M-PSK constellations,whereas it decreases as M increases for M-QAM constellations.

5.6.Influence of m for Nakagami-m channel

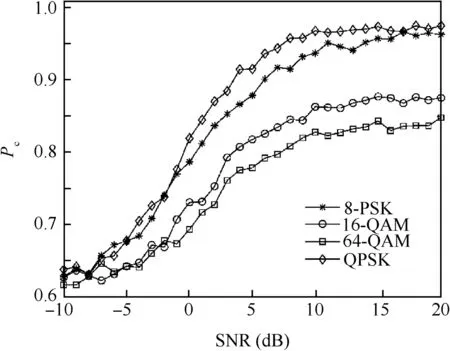
Fig.6 Effect of the modulation scheme on Pc.

Fig.7 Effect of m on Pc.

Fig.7 presents the performance of the proposed algorithm with respect to m for an interceptor with a single receiver antenna and 2048 samples.The simulation conditions as follows:the SM,Al,ST3 and ST3 are under consideration and PFA=10-2.The variance of the channel coefficients increases for lower m values,which affects the value of the variance of^C40,r(k),thus leading to erroneous results.

5.7.Performance comparison

Fig.8 compares the average probability of correct classification with the algorithms mentioned in Refs.14,15FOLP-A,FOLP-B and FOLP-C represent these algorithms in Refs.14,respectively.These algorithms14,15are sensitive to Gaussian noise and perform unsatisfactory at a SNR less than 5 dB.In addition,the algorithms mentioned in Ref.14merely discriminate between spatial multiplexing and Alamouti coding.The proposed algorithm performs well even at a SNR equal to 0 dB.This is due to the employment of the fourth-order cumulants,which are not sensitive to Gaussian noise.

We compare the performance of the proposed method with algorithms in Refs.14,15in detail below.The simulation conditions are different than in the Refs.14,15Ref.14investigated SM and Al signals for classification,and it did not involve the general STBCs.Ref.15investigated 4 STBCs.Table 3 and Table 4 compare the average probability of correct classification Pc,over Nakagami-m fading channel,m=3,for different values of SNR of the proposed algorithm and those algorithms in Refs.14,15For Table 3 and Table 4,the number of symbols are set to 1024 and 8192 respectively.The proposed algorithm exhibits superior performance,especially at a lower SNR.

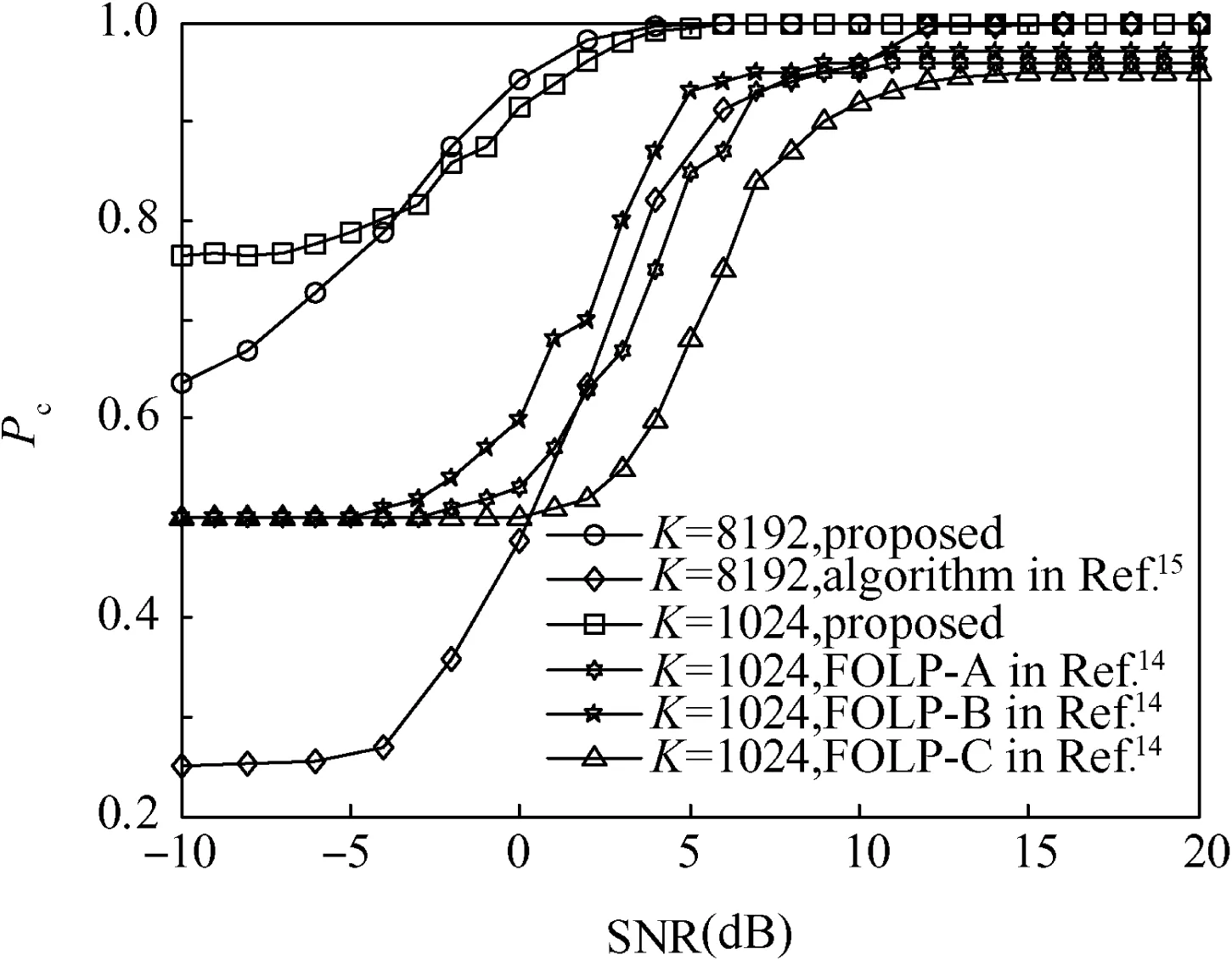
Fig.8 Comparison of algorithms in Refs.14,15

Table 3 Effect of SNR on Pcfor proposed algorithm,FOLPA,FOLP-B,and FOLP-C.

Table 4 Effect of SNR on Pcfor proposed algorithm and algorithm in Ref.15

In Table 5 and Table 6,the effect of the number of received symbols K on Pcat SNR=10 dB is presented for the proposed algorithm and the algorithms in Refs.14,15Increasing the number of symbols results in a performance improvement for the proposed algorithm due to a more accurate estimate of the fourth-order cumulantsIt is worth noting that the proposed algorithm outperforms those in Refs.14,15

Table 7 and Table 8 present the modulation scheme effect on Pcat SNR=10 dB for the proposed algorithm and the algorithms in Refs.14,15The proposed algorithm is independent of M for the M-PSK modulation(M≥4);it degrades slightly as M increase for M-QAM modulation.It should also be noted that less K is needed to attain a classification performance for M-PSK(M≥4)similar to that for M-QAM modulation.Forexample,for K=2048,Pc=0.9980 and Pc=0.9940 for the proposed algorithm,while Pc=0.8500 and Pc=0.7800 results from FOLP-C with 16-QAM and 64-QAM respectively.Therefore,the proposed algorithm outperforms those in Refs.14,15(see Tables 7 and Table 8).

Table 9 and Table 10 present the effect of m on Pcat SNR=10 dB for the proposed algorithm and the algorithms in Refs.14,15The proposed algorithm exhibits a lower sensitivity to m when compared with the algorithms in the Refs.14,15

Table 5 Effect of the number of symbols on Pcfor proposed algorithm,FOLP-A,FOLP-B,and FOLP-C.

Table 6 Effect of the number of symbols on Pcfor proposed algorithm and algorithm in Ref.15

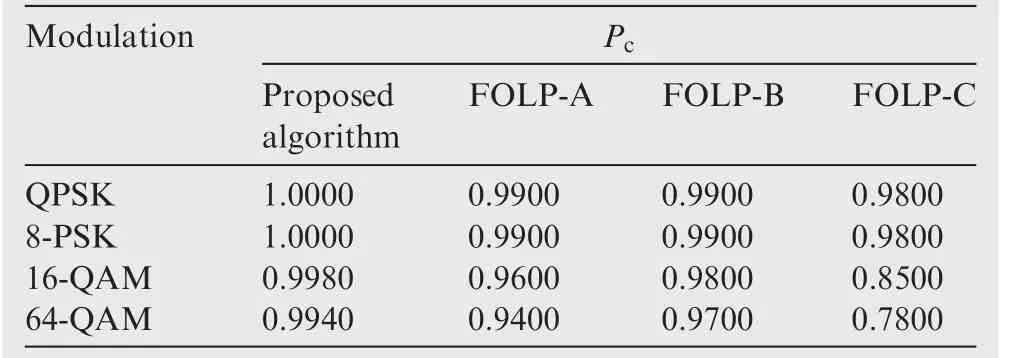
Table 7 Effect of modulation scheme on Pcfor proposed algorithm,FOLP-A,FOLP-B,and FOLP-C.

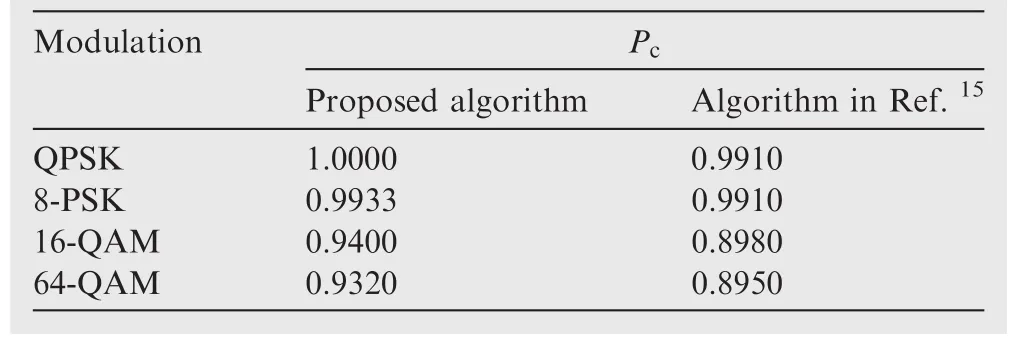
Table 8 Effect of modulation scheme on Pcfor proposed algorithm and algorithm in Ref.15

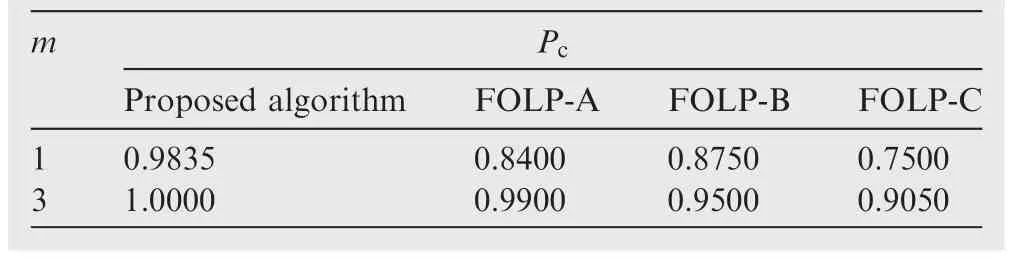
Table 9 Effect of the Nakagami-m on Pcfor proposed algorithm,FOLP-A,FOLP-B,and FOLP-C.

Table 10 Effect of the Nakagami-m on Pcfor proposed algorithm and algorithm in Ref.15

Table 11 presents the effect of PFA on Pcat SNR=10 dB for the proposed algorithm and the algorithm in Ref.14The two algorithms exhibit similar performance.

6.Conclusions

This paper proposes a novel method for blind classification of STBCs based on the fourth-order cumulants.It shows that the fourth-order cumulants of the STBCs exhibit non-null values that depend on the transmitted STBCs.The detection of nonnull values is performed through hypothesis testing,and automatic classification is done by decision tree.The proposed algorithm is evaluated for the classification of 4 STBCs with different code lengths:SM,Alamouti coding,and two kinds of orthogonal STBCs.The proposed algorithm operates well even at a low SNR with a single receiver antenna.The performance is enhanced by increasing the number of received samples.Additional experiments show that the probability of false alarm,modulation scheme and different Nakagami-m fading channels also influence the average probability of correct classification.

Acknowledgement

This study was co-supported by the Taishan Scholar Special Foundation of China(No.ts201511020).

1.Larsson E,Stoica P.Space-time block coding for wireless communications.Cambridge:Cambridge Press;2003.p.167–70.

2.Marey M,Dobre OA,Liao B.Classification of STBC systems over frequency-selective channels.IEEE Transactions on Vehicular Technology 2014;64(5):2159–64.

3.Choqueuse V,Marazin M.Blind recognition of linear space-time block codes:a likelihood-based approach.IEEE Transactions on Signal Processing 2010;58(3):1290–9.

4.Choqueuse V,Yao K.Hierarchical space-time block code recognition using correlation matrices.IEEE Transactions on Wireless Communications 2008;7(9):3526–34.

5.Choqueuse V,Yao K.Blind recognition of linear space time block codes.2008 IEEE international conference on acoustics,speech and signal processing;2008 Mar 31–April 4;Las Vegas,USA.Piscataway,NJ:IEEE Press;2008.p.2833–6.

6.Marey M,Dobre OA,Inkol R.Blind STBC identification for multiple antenna OFDM systems.IEEE Transactions on Communications 2014;62(5):1554–67.

7.Mohammadkarimi M,Dobre OA.Blind identification of spatial multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov(K-S)test.IEEE Communications Letters 2014;18(10):1711–4.

8.Eldemerdash YA,Dobre OA,Liao BJ.Blind identification of SM and Alamouti STBC-OFDM signal.IEEE Transactions on Wireless communications 2015;14(2):972–82.

9.Shi M,BAR-NESS Y.STC and BLAST MIMO modulation recognition.IEEE global telecommunications conference;2007 Nov 26–30;Washington D.C.,USA.Piscataway,NJ:IEEEPress;2007.p.3034–9.

10.Marey M,Dobre OA.Classification of space-time block codes based on second-order cyclostationarity with transmission impairments.IEEE Transactions on Wireless Communications 2012;11(7):2574–84.

11.Karami E,Dobre OA.Identification of SM-OFDM and ALOFDM signals based on their second-order cyclostationarity.IEEE Transactions on Vehicular Technology 2015;64(3):942–53.

12.De Young M,Heath R,Evans B.Using higher order cyclostationarity to identify space-time block codes.IEEE global telecommunications conference;2008 Nov30–Dec4;New Orleans,USA.Piscataway,NJ:IEEE Press;2008.p.1–5.

13.Choqueuse V,Mansour A,Burel G.Blind channel estimation for STBC system using higher-order statistics.IEEE Transactions on Wireless Communications 2011;10(2):495–505.

14.Eldemerdash YA,Marey M,Dobre OA.Fourth-order statistics for blind classification of spatial multiplexing and Alamouti spacetime block code signals.IEEE Transactions on Communications 2013;5(6):1–12.

15.Eldemerdash YA,Dobre OA,Marey M.An efficient algorithm for space-time block code classification.IEEE Global Communication Conference;2013 Dec 9–13;Atlanta,USA.Piscataway,NJ:IEEE Press;2013.p.3034–9.

16.Beaulieu NC,Cheng C.Efficient Nakagami-m fading channel simulation.IEEE Transactions on Vehicular Technology 2005;54(2):413–24.

17.Alamouti A.A simple transmit diversity technique for wireless communication.IEEE Journal on Selected Areas in Communications 1998;16(8):1451–8.

18.Tarokh V,Jafarkhani H,Calderbank A.Space time block codes from orthogonal designs.IEEE Transactions on Information Theory 1999;45(5):1451–8.

19.Swami A,Sadler BM.Hierarchical digital modulation classification using cumulants.IEEE Transactions on Communications 2000;48(3):416–29.

20.Zhang XD.Signal analysis and processing.Beijing:Tsinghua University Press;2011.p.314–5.

Ling Qingis a Ph.D.student at Naval Aeronautical and Astronautical University.She received her M.E.degree from same University in 2012.Her areas of research include the blind identification of channel coding and Satellite reconnaissance.

Zhang Liminis a professor and Ph.D.supervisor at Naval Aeronautical and Astronautical University.He received the Ph.D.degree from the Tianjin University in 2005.His current research interests are the blind identification of channel coding and Satellite reconnaissance.

Yan Wenjunreceived M.E.and D.E.degrees from Naval Aeronautical and Astronautical University in 2015,and then became a teacher there.His main research interests are the blind identification of channel coding and Satellite reconnaissance.

31 August 2015;revised 18 December 2015;accepted 24 January 2016

Available online 7 May 2016

Blind classification;

Fourth-order cumulants;

Multiple input single output;

Non-cooperative context;

STBCs

?2016 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 535 6635871.

E-mail address:iamzlm@163.com(L.Zhang).

Peer review under responsibility of Editorial Committee of CJA.