煤與瓦斯突出數學模型及三維數值模擬

劉雪琴，李會謙，馮 哲

（1.北京達飛安評管理顧問有限公司，北京 100101；2.北京礦冶研究總院，北京 100160；3.北京燃氣昌平有限公司，北京 102200）

煤與瓦斯突出數學模型及三維數值模擬

劉雪琴1，李會謙2，馮 哲3

（1.北京達飛安評管理顧問有限公司，北京 100101；2.北京礦冶研究總院，北京 100160；3.北京燃氣昌平有限公司，北京 102200）

為研究掘進過程中瓦斯壓力變化規律，從孔隙率定義出發推導出孔隙率與滲透率的動態模型方程，并通過建立含瓦斯煤壓力場控制方程得到含煤與瓦斯突出數學模型。以陽煤五礦趙家分區煤礦為例，通過FLUENT對建立煤與瓦斯突出數學模型進行了對應的三維數值模擬研究。結果表明，隨著掘進工作的進行，瓦斯卸壓區域漸漸擴大，滲透率隨之改變，最后瓦斯流動速率慢慢加快，離掘進面愈近的地點瓦斯壓力降低速率愈高。在具備了瓦斯異常涌出的物質、動力和構造條件后，深部含瓦斯煤層在很大程度上會伴有瓦斯異常涌出和瓦斯濃度超標的現象，對現場瓦斯防治工作提供相應理論指導。

煤；瓦斯；突出數學模型；三維數值；模擬；參透率

我國95%的煤炭屬于地下開采，賦存條件差，在煤礦深部巷道掘進的過程中，由于地應力及地質條件的影響，會引起圍巖變形破壞，導致煤與瓦斯突出事故，嚴重威脅著煤礦安全高效生產和礦山工作人員的生命安全。因此對于煤與瓦斯突出的研究工作擁有特別重要的理論和實際意義［1-2］。文章通過對煤與瓦斯運移規律進行研究來預測、控制及防止煤和瓦斯突出這一災害，結合理論方程，針對陽煤五礦趙家分區的地質情況和開采技術條件構建煤與瓦斯突出數學模型，運用FLUENT對建立的數學模型進行了對應的三維數值模擬研究，對深入認識煤與瓦斯突出機理、指導預防措施等具有理論意義和實用價值。

1　瓦斯流動數學模型

1.1 模型構建的基本假設

深層煤巖體施工過程復雜，所有的因素不能一一考慮，為更精確地描述受擾動影響的含瓦斯煤體的氣固相互影響作用，引入如下幾個基本假設［3-5］：①含瓦斯煤體為各向同性彈塑介質；②在瓦斯運移和煤體變形過程中溫度保持不變；③含瓦斯煤體的變形為小變形；④瓦斯在煤巖中的滲流服從Darcy定律；⑤瓦斯的吸附解服從Langmuir平衡方程，并且假設煤體只吸附瓦斯。

1.2孔隙率和滲透率動態模型方程

含瓦斯煤巖在加載過程中，隨著變形的增加，等效孔隙度（φ）和滲透率（k）是動態變化的。在建立含瓦斯煤巖本構模型時，應考慮這些因素的變化和影響。

（1）孔隙率動態模型。①當含瓦斯煤巖處于彈性變形階段時。孔隙率是孔隙裂隙介質體積與多孔介質總體積之比。含瓦斯煤體的孔隙率是動態變化的，設煤固體骨架體積用表示，表示其變化；煤外觀總體積用表示，表示其變化，煤的孔隙體積用表示，表示其變化。由孔隙率的定義可知［6］：

巖石試件在受壓情況下，當達到峰值強度時，開始出現宏觀裂紋。因此，可假設當載荷達到峰值應力時的，可由實驗得到；而當載荷達到屈服應力時，有。根據這兩種情況，不難推導出，，并將之回代入式（2），得到：

（2）滲透率動態模型。當煤體的孔隙率發生動態變化時，滲透率隨之而變，從而影響煤體內瓦斯流動［7］。

根據Carman-Kozeny經驗公式：

假設初始狀態煤體滲透率為：

孔隙體積的變化為：

改變后的孔隙率為：

1.3含瓦斯煤壓力場控制方程

（1）滲流運動方程。研究表明瓦斯在低滲透率多孔介質中運移時，在固體壁面存在滑脫效應［8］。陽煤五礦趙家分區15#煤層多為高瓦斯及低滲透煤層，因此，考慮滑脫效應時，煤層中瓦斯的運動方程可表示為：

（3）煤體瓦斯含量方程。瓦斯氣體的解吸和吸附隨瓦斯壓力變化的關系滿足朗格繆爾方程，所以有煤層吸附瓦斯含量計算公式［9］為例：

式中，a為吸附常數，m3/kg，b為吸附常數，MPa-1，c為煤質校正參數，kg/m3，，為煤的密度，kg/m3；M為煤的水分，%；A為煤的灰分，%。煤層中游離瓦斯氣體含量為：

（4）滲流連續方程。根據質量守恒定律，煤層瓦斯流動的方程為：

式中：M為煤體瓦斯瓦斯含量；V為瓦斯滲流速度，m/s。聯合式（1），（10） ～ （13），可得滲流方程為：

2　數值模擬及結果分析

2.1幾何模型的建立

根據假設條件，以陽煤五礦趙家分區內15號煤層賦存為依據，對依據模型的幾何尺寸構建三維計算進行網格劃分，細化煤層以及周圍的巖網格適當粗劃剩下網格部分，最后總共劃了207 200個單元，218 766個節點。煤層原始瓦斯壓力為1.0MPa，在模型頂部施加20.17MPa的均布載荷用來模擬上覆巖層自重作用，底部為固定邊界，前后左右設定為法向約束邊界。

利用煤巖體變形與瓦斯滲流相互作用下的彈性損傷程序進行數值計算，表1為瓦斯流動計算的相關參數。

表1　煤層主要相關物性參數

2.2三維數值模擬結果分析

根據以上條件，對該模型進行數值模擬，以8134工作面上順槽獨巷掘進為對象進行模擬計算。當地應力達到真實情況之后，對巷道內單元設置為空單元。煤體掘進后造成應力場的重新分布，對開挖過程后的滲流場數值模擬結果進行分析。

在獨巷掘進過程中，處于掘進工作面前方煤體中的裂隙持續變化，煤體中的瓦斯在這些孔隙中流動，由于擴散效應，瓦斯從高濃度流向低濃度空間，到達巷道中。獨巷掘進開采時，破壞了巷道周圍的煤巖，巷道圍巖應力重新分布，損傷逐漸加劇，裂隙重組，煤層的孔隙率和滲透率隨之改變。對孔隙率和滲透率進行歸一化處理，圖1、圖2 分別表示掘進開采時前方煤體孔隙率比率和滲透率比率的規律分布。

圖1　掘進面前方煤體孔隙率比率分布規律

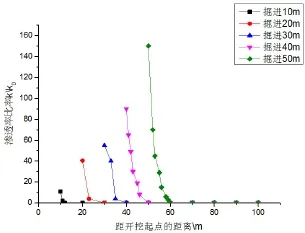
圖2　掘進面前方煤體滲透率比率分布規律

通過FLUENT軟件根據得到的孔隙率和滲透率的變化分布規律，對五礦趙家分區獨巷掘進過程中的瓦斯壓力變化規律模擬分析。滲流場初始化為均勻分布的瓦斯壓力，并固定模型邊界位置的瓦斯壓力值，在巷道開挖后，對挖空單元賦予固定的大氣壓力值。同時為了簡化模型，提高計算速度，假設整個模型中煤層厚度很大，忽略了支護結構和巖層的影響。

圖3至6分別給出了煤巖巷道橫切面（x=0）和縱切面（z=12）上，在掘進過程中煤巖體中瓦斯壓力的變化規律。開挖深度分別為10m、20m、30m、50m。

圖3　開挖10m 時瓦斯壓力變化分布規律

圖4　開挖20m 時瓦斯壓力變化分布規律

圖5　開挖30m 時瓦斯壓力變化分布規律

圖6　開挖50m 時瓦斯壓力變化分布規律

由圖3至6可以看出，當開挖到10m時，開始階段，圍巖破壞較輕，煤體滲透率較低，導致瓦斯涌入巷道內的流動速度較慢，同時圍巖內瓦斯由于壓力降低而不斷解吸，所以在當開挖10m時，瓦斯壓力降低較小，在距離巷道0.7m以內的圍巖卸壓明顯。隨著繼續向前掘進，當開挖到20m時，由于圍巖破損提高了煤體的透氣性，瓦斯流動速度增加，瓦斯壓力降低范圍增大，距離巷道1m以內的圍巖卸壓明顯。當開挖到30m時，瓦斯壓力降低范圍逐漸增大，距離巷道1.5m以內的圍巖卸壓明顯。當開挖到50m時，距離巷道3m以內的圍巖卸壓明顯，最小瓦斯壓力約為0.231MPa。在靠近煤巷壁面的位置，煤體破損嚴重，造成瓦斯釋放完全，瓦斯壓力值較低。

2.3工作面掘進過程中煤體瓦斯壓力變化規律

為更加具體地研究工作面掘進過程中煤體瓦斯壓力變化規律，在煤層中沿工作面掘進方向巷道中心線上瓦斯壓力變化曲線如圖7所示。

圖7　工作面掘進方向煤層瓦斯壓力變化分布曲線

從圖7可知，在巷道持續掘進過程中，當開始掘進10m時，掘進面前方的瓦斯壓力緩慢降低，影響范圍較小。在繼續開挖的過程中，隨著時間的延長，掘進面前方煤層損傷程度及范圍繼續擴展，同時，卸壓影響范圍明顯擴大，壓力值顯著降低。當掘進到50m位置時，瓦斯壓力降低梯度也明顯增大，滲透率顯著提高。這都是因為掘進對于煤層的影響，致使掘進面前方的煤體產生了很多裂隙，滲透率漸漸升高，未開挖處煤層中的高濃度瓦斯經此通道流向巷道中，引起瓦斯壓力在掘進面前方重新分布。

3　結論

（1）隨著掘進工作的進行，由于掘進對于煤層的影響，致使掘進面前方的煤體產生了很多裂隙，掘進面前方高濃度瓦斯經裂隙流向巷道，引起瓦斯壓力在掘進面前方重新分布。瓦斯卸壓區域漸漸擴大，滲透率隨之改變，最后瓦斯流動速率慢慢加快，離掘進面愈近的地點瓦斯壓力降低速率愈高。

（2）深部開采的煤層中，在開采震動和擾動下，煤層裂隙中瓦斯解吸膨脹的能量和動力很高。開挖加、卸載下的層裂、離層與瓦斯解吸膨脹相互作用模式，和地下開挖導致應力重新分布，導致煤巖體產生微破裂，產生貫通裂帶。瓦斯通過裂隙大量涌出，造成圍巖瓦斯壓力下降，致使煤體有效應力增高，煤體進一步損傷破裂。因此，在具備了瓦斯異常涌出的物質、動力和構造條件后，深部含瓦斯煤層在很大程度上會伴有瓦斯異常涌出和瓦斯濃度超標的現象。

［1］ 李曉泉.含瓦斯煤力學特性及煤與瓦斯延期突出機理研究［D］.重慶大學，2010.

［2］ HiIdenbrand A，Krooss B M，Busch A.EvoIution of methane sorption capacity of coaI seams as a function of buriaI history：A case study from the Campine Basin ［J］. Int.J.CoaI GeoI，2006，（66）.179-203.

［3］ 汪有剛，劉建軍，楊景賀，等.煤層瓦斯流固耦合滲流的數值模擬［J］.煤炭學報，001，26（3）：286-289.

［4］ 梁冰，劉建軍，范厚彬，等.非等溫條件下煤層中瓦斯流動的數學模型及數值解法［J］.巖石力學與工程學報，2000，19（1）：1-5.

［5］ 薛東杰，周宏偉，唐咸力，等.采動煤巖體瓦斯滲透率分布規律與演化過程［J］.煤炭學報，2013，38（6）：32-37.

［6］ 李培超，孔祥言，盧德唐.飽和多孔介質流固耦合滲流的數學模型［J］.水動力學研究與進展（A輯），2003，18（4）：419-426.

［7］ 陳育民. FLAC/FIAC3D基礎與工程實例（第二版）［M］.北京：中國水利水電出版社，2013.

［8］ 肖遠見.沿層鉆孔周圍瓦斯（真實氣體）滲流壓力方程及三維數值分析［J］.礦業安全與環保，2004，31（3）：41-43.

［9］ 郭平，曹樹剛，張遵國，等.含瓦斯煤體固氣禍合數學模型及數值模擬［J］.煤炭學報，2012，37（增2）：330-335.

Mathematical Model and Three-dimensional Numerical Simulation of Coal and Gas Outburst

Liu Xueqin1，Li Huiqian2，Feng Zhe3
（1.Beijing Dafei Risk Assessment and Management Adviser Co.Ltd. Beijing， 100101； 2.Beijing General
Research Institute of Mining and Metallurgy， Beijing，100160； 3.Beijing Gas Changping Co.Ltd. Beijing，102200）

To obtain gas pressure variation in the process of coal mine roadway drivage， the dynamic model equation of porosity and permeability were derived in terms of the basic definition of porosity， and building coal-bearing and gas outburst mathematical model by coal containing gas pressure control field equation. According to the coalmine of Yangmei Minmetals， FLUENT was used to three-dimensional numerical simulation of mathematical model of coal and gas outburst. The result shows that gas pressure relief area gradually expanded， and permeability changed， finally gas flow rate accelerated slowly. The closer the driving surface is， the higher gas pressure reduction rate is. So it has significant means for guiding the gas drainage design.

Coal ；gas；outburst mathematical model；three-dimensional numerical；simulation；Permeability

TQ018

A

1671-3818（2016）09-0022-04