板式換熱器傳熱特性數值模擬與參數優化

張玉寶，徐海洋

（中車齊齊哈爾車輛有限公司，黑龍江齊齊哈爾161002）

板式換熱器傳熱特性數值模擬與參數優化

張玉寶，徐海洋

（中車齊齊哈爾車輛有限公司，黑龍江齊齊哈爾161002）

以工業廣泛使用的板式換熱器為研究對象，模擬了人字型波紋板片組成的冷熱雙流體通道的流動和換熱，分析了板式換熱器流道內的速度場、溫度場和壓力場，研究了波紋板片的幾何參數對傳熱特性的影響規律。以傳熱過程中產生的火積耗散為目標函數，采用序列二次規劃法（NLPQL）對波紋板片的結構參數進行了優化，優化后傳熱性能明顯提高。

板式換熱器；數值模擬；NLPQL；參數優化

0　引言

能源需求量的持續增長成為制約我國經濟發展的核心問題之一，解決辦法是除了改變能源結構，發展新能源外，另一個重要方向是提高能源利用效率。

板式換熱器作為一種重要的換熱設備，因換熱效果好、結構緊奏、易清洗、占地面積小等優點，近幾十年已廣泛應用于制冷、化工、石油、航空、航天等工業領域中。與其他形式的換熱器相比，板式換熱器在運行過程中存在流動阻力大、承溫承壓能力低等缺點[1-3]。因此，針對板式換熱器進行優化研究，以提高換熱效果、降低流動阻力、節能降耗，具有重要的研究意義。

采用數值模擬的方法，先對板式換熱器進行流動和換熱性能的分析，然后以傳熱過程中火積耗散最小為目標函數，采用NLPQL算法對板式換熱器結構參數進行了優化，得到了板式換熱器換熱性能最佳的波紋板片參數配置。

1　數值計算模型與網格劃分

1.1物理模型

文章對波紋板換熱主流區域進行建模，研究其換熱與阻力特性。圖1為雙流體通道計算模型，冷熱流體單邊逆向流動，上側流道為冷流體，右端流入，左側流出；下側流道為熱流體，左側流入，右側流出。

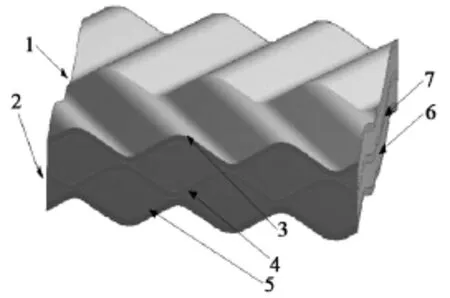
圖1　雙流體通道計算仿真模型

1.2數學模型

相關的控制方程如式（1）～（3）：

連續性方程：

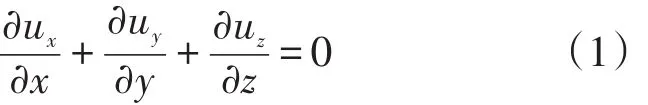
式中：ux、uy、uz分別為x、y、z方向上的速度分量，m/s。

動量方程：

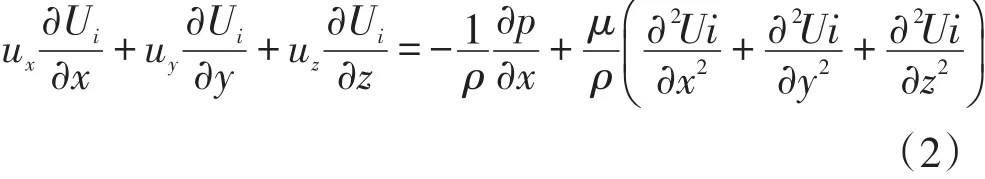
式中：i為方向；Ui為i方向上的速度分量，m/s；ρ為流體密度，kg/m3；p為壓力分量，Pa；μ為動力黏度，kg/（m·s）。

能量守恒方程：

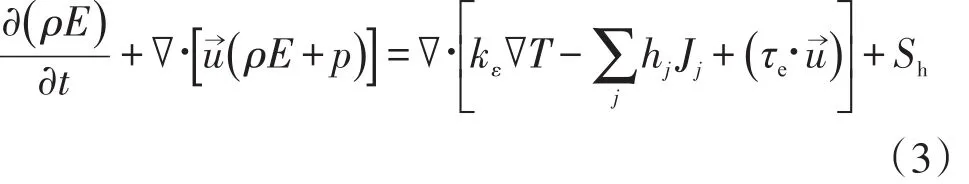
式中：E為流體微團的總能，J/kg，包含內能、動能和勢能之和；h為焓，J/kg；hj為組分j的焓，J/kg；kε為有效熱傳導系數，W/（m·K）；Jj為組分j的擴散通量；Sh為包括了化學反應熱及其他用戶定義的體積熱源項。

RNGk-ε方程：

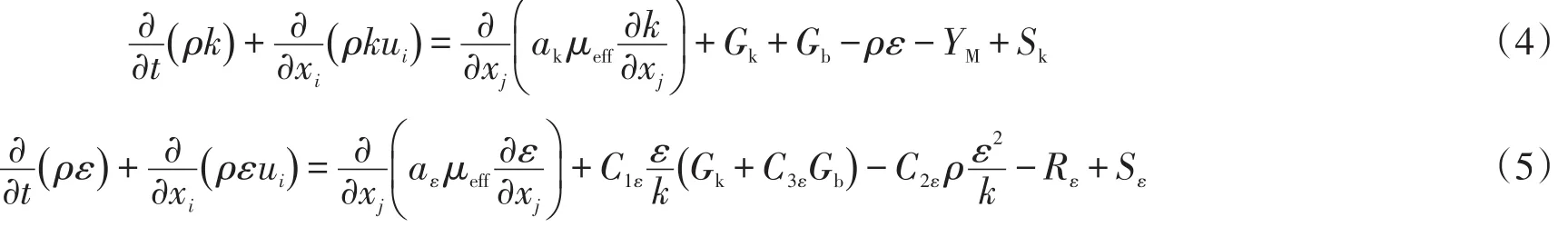
式中：Gk為由于平均速度梯度引起的湍流動能產生；Gb為由于浮力引起的湍流動能產生；YM為可壓縮湍流脈動膨脹對總的耗散率的影響；C1ε=1.44、C2ε= 1.92、C3ε=0.99、Cμ=0.09，湍流動能k與耗散率ε的湍流普朗特數分別為σk=1.0，σε=1.3。

1.3邊界條件的設定

進出口邊界條件：進口采用速度入口邊界條件，熱流體進口溫度為360 K，冷流體進口溫度為300 K。冷熱出口采用壓力出口邊界條件，出口靜壓設定為標準一個大氣壓。

壁面邊界條件：外部邊界為無滑移速度邊界條件，冷熱流道相接觸的面設定為耦合換熱面，其余各面設定為絕熱邊界條件。

1.4網格劃分

由于換熱器中波紋板間流道復雜多變，板式換熱器結構的三維實體模型采用Patch Independent、sizing四面體網格劃分算法，最小單元尺寸為0.8 mm。網格劃分如圖2所示。

2　數值計算方法

由于研究的傳熱問題不涉及相變，冷熱流體通道內的溫差較小，因此假設：（1）流體流動為定常流動，流體為不可壓縮的牛頓流體；（2）重力和由于密度差異引起的浮升力忽略不計；（3）流體的熱物理性能，被認為與溫度和壓力無關，通道中冷熱流體的流量分配均勻，考慮流體的黏性耗散作用。

圖2　模型網格劃分圖

采用FLUENT 12數值求解雙流體通道波紋板式換熱器的對流換熱過程，壓力與速度的耦合采用PISO算法，控制方程中的對流項和擴散項的離散均采用二階迎風格式，數值模擬仿真時采用RNGk-ε湍流模型。

3　數值模擬結果與分析

3.1流道內的速度場、溫度場和壓力場

圖3為波紋板式換熱器流道內截面Y=1.6 mm速度云圖。從圖可以看出，流體受到兩側波紋板的排擠作用，流體在波紋通道內主要是沿著流道方向運動。由于波紋板片是反向180°布置，流體在溝槽的折返流動時會改變流動方向，同時也會受到相對于波紋板片流體作用的切向力，這種切向力可以使流體產生漩渦和增大強化傳熱的作用。

圖3　波紋板式換熱器流道內截面Y=1.6 mm速度云圖

圖4為波紋板式換熱器流體通道內截面為Y= 1.6 mm壓力云圖。流體沿X軸正向流動，下面為進口，上面為出口。從圖可以看出，壓力梯度的變化分布沿主流方向上呈逐漸降低的變化，在流體入口處壓力梯度變化較大，總體上壓力梯度變化較為均勻。

圖4　波紋板式換熱器流體通道內截面Y=1.6 mm壓力云圖

圖5為波紋板式換熱器通道內冷熱流體通道溫度變化云圖，（a）為冷通道溫度變化云圖；（b）為熱通道溫度變化云圖。從圖可以看出，當流體進入波紋板通道時，熱流體區域沿流動方向（沿X軸正方向）溫度逐漸降低，冷流體沿著流動方向（沿X軸正方向）溫度逐漸升高。由于冷熱流體通過波紋板耦合傳熱，所以熱流體區域溫度降低的程度要比冷流體區域溫度升高的程度大一點。熱流體通道的流體溫差變化較大，而冷流體通道內的流體溫差變化不大。

圖5　波紋板式換熱器通道內流體通道溫度變化云圖

3.2波紋傾角對傳熱特性影響

努謝爾特數是表示壁面上對流換熱系數的無量綱表達形式之一，大小表示了對流換熱的強弱[4]。

在波紋板片的其他參數不變的情況下，模擬計算了波紋傾角β在40°、50°、55°、60°、70°、80°時板式換熱器的傳熱特性和壓降特性。圖6為波紋傾角β和努謝爾特數Nu的變化關系。從圖可以看出，β在60°附近時努謝爾特數最大、傳熱特性最優。

3.3波紋節高比對傳熱特性影響

在波紋傾角為60°不變的情況下研究不同的波紋節高比對換熱和壓降的影響規律。圖7為努謝爾特數隨著波紋節高比變化情況。

從圖7可以看出，隨著波紋節高比的增大，傳熱系數有明顯的下降趨勢，也就是說波紋法向距離越大，波紋高度越小，其傳熱的效果越差。但當波紋節高比大于6.19時會有所提高，經過計算節高比在6.19時雷諾數為1 085。雷諾數大于這個值的時候采用大的波紋節高比的波紋板片時換熱效果比較好，雷諾數小于這個值的時候選擇波紋節高比越小的板片傳熱效果越好。

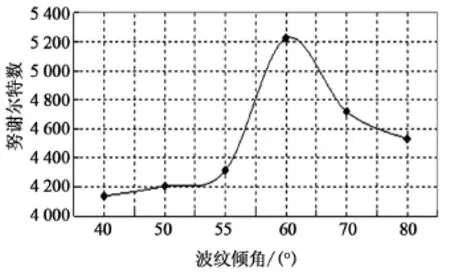
圖6　努謝爾特數隨波紋傾角的變化曲線圖

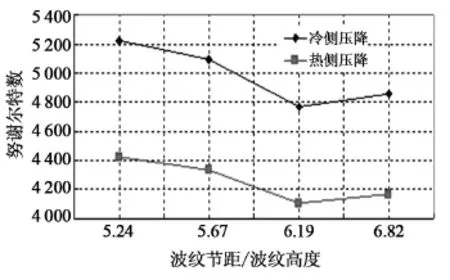
圖7　努謝爾特數隨波紋節高比的變化曲線圖

4　波紋板參數優化

采用序列二次規劃法（NLPQL）這一數學優化方法，結合人字形板式換熱器的仿真模型，可以進行波紋板的參數優化設計。

4.1目標函數的選擇

板式換熱器的傳熱過程主要是由冷熱流體之間的有限溫差進行耦合換熱。這部分引起的耗散是重要的，采用有限溫差引起的耗散最小為目標函數。

有限溫差引起的耗散的表達式（6）[5]：

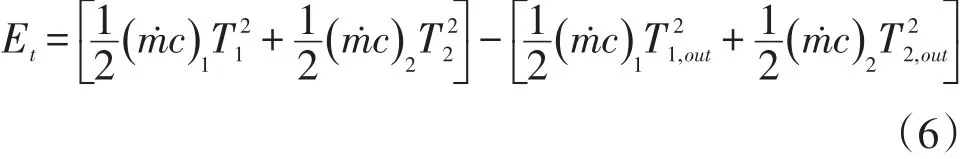
式中：m?為質量流量；c為比熱容；T1為熱流體入口溫度；T2為冷流體入口溫度；T1,out為熱流體出口溫度；T2,out為冷流體出口溫度。

4.2優化算法NLPQL

NLPQL（Nonlinear Programming Quadratic Line search）[6]是一種基于采用目標函數和約束梯度來解決非線性優化問題的標準方法。用于求解一般的有約束條件的最優化問題，具有整體收斂性且同時保持局部收斂性，被認為是當今求解非線性問題的最優的算法之一。

該算法需要AWE（ANSYS Workbench Environ?ment）來計算目標函數和約束在設計空間所有方向上的梯度，AWE使用有限差分法來計算這些梯度值。優化設計程序框圖如圖8所示。

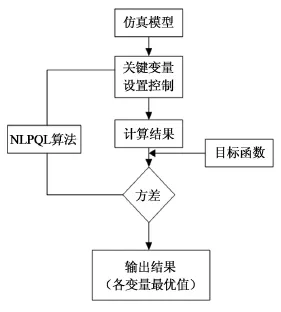
圖8　優化設計程序框圖

4.3優化結果

從圖9觀察到，頂部深灰色區域的火積耗散值大，換熱效果不好，底部深灰色區域的耗散值小，表征傳熱效果好。用Design Exploration模塊經過仿真優化計算，得出波紋板優化前后的參數如表1所示。

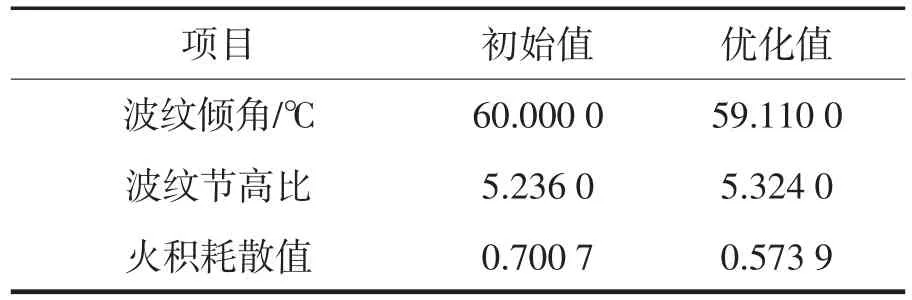
表1　NLPQL優化前后參數變量值

從表1可以看出，基于NLPQL算法的板式換熱器的優化設計，優化前火積耗散值為0.700 7，優化后為0.573 9，傳熱特性提高18.1%，換熱效果明顯改善，最佳波紋配置參數為波紋傾角為59.11°，波紋節高比為5.236。這為改進型板式換熱器研究開發提供了理論基礎。

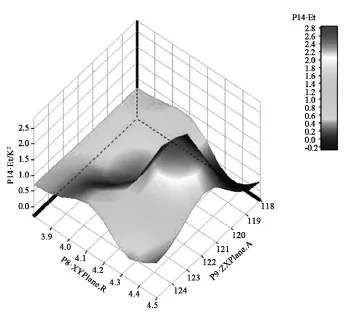
圖9　波紋傾角、節高比與火積耗散關系圖

5　結論

利用數值模擬方法模擬了板式換熱器雙流體通道耦合換熱情況，分析了換熱器的速度場、溫度場、壓力場，并分析了波紋傾角、波紋節高比對傳熱系數的影響規律，60°附近的波紋傾角傳熱系數最大，換熱效果最好；波紋節高比對傳熱系數的影響規律是先減小后增大，節高比為6.19是一個轉折點。基于序列二次規劃法（NLPQL）算法對波紋板片結構參數進行優化計算，以板式換熱器傳熱過程中有限溫差引起的火積耗散為目標函數，根據火積耗散極值原理，以火積耗散數最小為目標對板式換熱器進行優化。優化后系統產生的耗散值較優化前明顯減小，傳熱特性明顯提高。

[1]吳晶，夏夢，葉莉，等.板式換熱器強化傳熱數值研究及熱阻分析[J].工程熱物理學報，2012，11（33）：1963-1966.

[2]張仲彬，董鵬飛，王月明，等.板式換熱器結構優化三維數值分析[J].化工機械，2013，40（2）：206-210.

[3]邵擁軍，逯凱霄，張文林.板式換熱器的特點與優化設計[J].廣州化工，2012，40（6）：120-122.

[4]Kanaris A G，Mouza A A，Paras S V.Optimal design of a plate heat exchanger with undulated surfaces[J].International Jour?nalofThermalSciences，2009，48（6）：1184-1195.

[5]Doo JH，Yoon HS，Ha MY.Study on improvementofcompact?ness of a plate heat exchanger using a newly designed primary surface[J].International Journal of Heat and Mass Transfer，2010，53（25）：5733-5746.

[6]Guo Z Y，Zhu H Y，Liang X G.Entransy—a physical quantity describing heat transfer ability[J].International Journal of Heatand Mass Transfer，2007，50（13）:2545-2556.

NUMERICAL SIMULATION AND PARAMETER OPTIMIZATION ON TRADITIONAL PROPERTIES OF PLATE HEAT EXCHANGER

ZHANG Yu-bao，XU Hai-yang
（Qiqihaer Zhongche Vehicle Co.Ltd，Qiqihaer Heilongjiang 161002，China）

Plate heat exchanger，which is widely used in industrial，is used as the research object to simulate flow of fluid channel and heat transfer of hot and cold dual-channel consisted of the herringbone corrugated plates，and analyze the velocity field，temperature field and pressure field of plate heat exchanger’s flow passage，study the influence law of the corrugated board sheet’s geometric parameters on heat transfer characteristics.Dissipation generated in the heat transfer process is used as the objective function to optimize the corrugated board sheet’s structure parameters which used sequential quadratic programming（NLPQL）.Heat transfer performance after optimization of the heat exchanger has improved significantly.

plate heat exchanger；numerical simulation；NLPQL；parameter optimization

TB657.5

A

1006-7086（2016）05-0296-05

10.3969/j.issn.1006-7086.2016.05.011

2016-05-24

張玉寶（1987-），男，哈爾濱人，工程師，主要從事制冷技術研究。E-mail：zhangyubaohappy@163.com。