基于MIDAS—GTS的滲流—應力耦合作用下邊坡穩定性分析
張江昊
(西安科技大學地質與環境工程系,陜西 西安710054)
基于MIDAS—GTS的滲流—應力耦合作用下邊坡穩定性分析
張江昊
(西安科技大學地質與環境工程系,陜西 西安710054)
土質邊坡中的地下水滲流作用主要涉及水力學和土力學相互作用的問題。地下水位升降產生的滲流—應力耦合作用對邊坡穩定性會產生顯著的影響。主要分析了土顆粒微元體在滲流中的受力狀態,并據此得出應力—滲流耦合方程,在此基礎上,結合MIDAS—GTS中的滲流分析模塊及邊坡穩定性分析模塊(SRM),得出滲流—應力耦合作用對邊坡穩定性的影響大小。
MIDAS—GTS;滲流—應力耦合;邊坡工程;有限元;穩定性
1 土體顆粒在滲流場中的受力分析
邊坡中的滲流主要有以下4種情況:水平方向滲流、平行坡面方向滲流、自下而上方向滲流、垂直向下方向滲流。不同滲流方向在土體顆粒中產生不同方向的滲流作用力,根據力的平行四邊形法則,將土體顆粒所受的滲流作用力分解為垂直于顆粒表面的動水壓力和與顆粒表面相切的水流摩擦力。因此,在土體中任取一微元體,將滲流作用力F分解為鉛直向上的分力u與沿流線方向的分力fs,即靜水壓力產生的浮力u與動水壓力產生的滲透力fs。,如圖1所示。

圖1 土體微元體在滲流場中的受力示意圖
浮力u和動水壓力產生的滲透力fs分別為:

式中:n為孔隙率;γw為水容重;JW為滲流水頭坡降。
2 應力—滲流耦合效應
地下水位的變化必然會產生土體顆粒附近的水頭差,由此產生的滲透力差異必然會引起土體應力場和位移場的變化。同時,應力場和位移場的改變又將引起土體孔隙率的改變,孔隙率的改變又會引起土體滲透性的改變,從而引起滲流場的變化。因此,土體應力和滲流作用力是相互制約和相互影響的,這種效應稱為滲流—應力耦合作用。
考慮有效應力原理的微元體三維平衡方程如下:

以位移和孔隙水壓力表示的連續性方程如下:
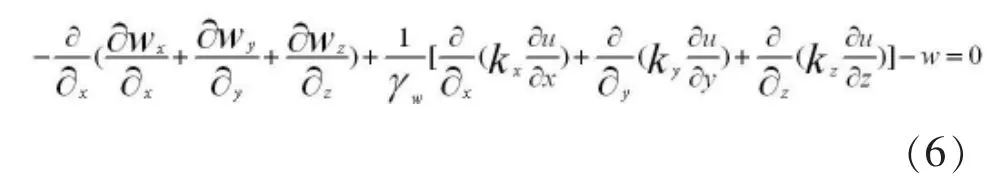
土中任一點的孔隙水壓力變化和位移變化必須同時滿足平衡方程(3)(4)(5)和連續性方程(6),將兩式聯立起來便是土體中的滲流—應力耦合方程。
3 基于MIDAS-GTS的有限元模擬
有限元強度折減法是通過不斷降低邊坡巖土體抗剪強度參數直至達到極限破壞狀態為止,程序
會自動根據彈塑性有限元計算結果得到滑動破壞面,同時得到邊坡的強度儲備安全系數。這種方法十分貼近工程設計。
MIDAS-GTS進行滲流作用下的邊坡穩定性分析,只需建立一個有限元計算模型。它既可以進行考慮最終穩定狀態或考慮時間效果的滲流分析,也可以將滲流分析得到的孔隙水壓力與應力耦合進行有效應力分析,故選用MIDAS-GTS進行數值模擬計算。
算例:均質土質邊坡,坡高H=20m,坡角27°,粘聚力c=20KPa,內摩擦角φ=15°,,泊松比υ=0.3,彈性模量E=3000KPa,滲透系數kx=ky=0.001m/d。水頭荷載一:在左側邊界和坡下邊界施加水頭荷載H= 20m;水頭荷載二:在左側邊界和坡下邊界施加水頭荷載H=20m。假定兩種水頭荷載下邊坡中的滲流為穩定流,計算模型如圖2所示。

圖2 有限元模型
通過計算得到天然工況、水頭荷載一和水頭荷載二時的安全系數和滑動面位置,如圖3所示。

圖3 天然工況下的安全系數和滑動面位置

圖4 水頭荷載一時的安全系數和滑動面位置

圖5 水頭荷載二時的安全系數和滑動面位置
由圖3、4、5分析可得,天然工況下邊坡安全系數為1.5375,邊坡處于極其穩定的狀態。水頭荷載一時的邊坡安全系數為1.2875,安全系數有所減小,邊坡仍處于穩定狀態,但對某些安全系數要求較高的重要工程,則需進行邊坡加固(安全系數K>1.2875時)。水頭荷載二時的邊坡安全系數為0.9625,此時邊坡已處于不穩定狀態。滑動面起點距坡肩的距離顯著增大,滑動面形態顯著變化。由于滲流作用的影響,坡肩附近的土體位移明顯增大,而剪出口處的土體位移變化不大,說明滲流作用對邊坡穩定性的影響主要集中在坡肩附近一定范圍內。因此,建議在今后的邊坡治理工程中重視對坡肩附近坡體進行加固,防止在此區域產生二級或多級滑動面。
4 結論
本文利用MIDAS-GTS軟件并結合算例,考慮在滲流—耦合作用下,對不同水頭荷載時邊坡穩定性的影響進行了研究。通過數值模擬計算得出,滲流作用對邊坡穩定性影響顯著,當水頭荷載達到一定程度時,會使坡肩附近區域土體位移量顯著增大,對邊坡穩定性不利,在今后的工程設計治理中要注意加強防范。
[1] 謝羅峰.滲流作用下邊坡穩定性研究[D].南京水利科學研究院,2009.
[2] 華洪勛.考慮滲流影響與分步開挖的基坑變形性狀分析研究[D].廣東工業大學,2008.
[3] 郭玉龍.滲流與應力耦合對邊坡穩定性影響的研究[D].武漢理工大學,2008.
[4] 鄭穎人,陳祖煜,王恭先,等.邊坡與滑坡工程治理[M].人民交通出版社,2010.
[5] 王海濤.MIDAS/GTS巖土工程數值分析與設計[M].大連理工大學出版社,2013.
P642

