采用神經網絡提高EIT成像質量的方法研究

陳曉艷，師 波，褚猛麗，楊 濤

（天津科技大學電子信息與自動化學院，天津 300222）

采用神經網絡提高EIT成像質量的方法研究

陳曉艷，師 波，褚猛麗，楊 濤

（天津科技大學電子信息與自動化學院，天津 300222）

提出了一種采用神經網絡提高EIT成像質量的方法.首先，根據電阻抗成像原理，構建了208-10-208三層神經網絡.然后，將實驗平臺上采集的實測數據分為訓練數據和成像數據，將根據仿真模型求解得到的仿真數據作為期望值，利用訓練數據對神經網絡進行訓練，獲得神經網絡參數，建立神經網絡模型；將成像數據作為訓練好的神經網絡的輸入，利用神經網絡的輸出數據重建圖像.最后，采用6項指標對神經網絡訓練前后的重建圖像效果進行評價.結果表明：采用神經網絡后的圖像在相關系數、結構相似度、相對誤差、位置誤差、外形形變、瞬時震蕩6項指標上均有顯著提高.

神經網絡；電阻抗成像；圖像重建；圖像評價

電阻抗成像（electrical impedance tomography，EIT）是一種非侵入式檢測成像技術，其基本原理是根據物場內介質的阻抗（電阻/電導率）特征，采用給物場施加激勵電流或電壓來測量響應電壓或電流，重建物場內部的電導率分布或其變化的圖像.電阻抗成像技術在解決實際問題中存在很多難點與挑戰，提高圖像分辨率是最具挑戰的研究課題.諸多國內外學者從圖像重建算法角度研究了如何提高圖像成像質量，比如基于 LM 的電阻抗成像的圖像重建算法［1］、PEPR算法［2］.采用神經網絡提高 EIT成像質量的研究也有報道，如：Michalikova等［3］采用徑向基函數（RBF）神經網絡進行圖像重建，謝莉莉等［4］提出了采用 PSO算法優化 BP神經網絡的 EIT圖像重建算法，都是將敏感場邊界電壓值作為神經網絡輸入量，將有限元電阻率/電導率作為神經網絡輸出量，進行逆問題計算，從而達到提高重建圖像質量的目的.

本文提出通過神經網絡對邊界測量電壓值進行訓練的方法，以充分利用神經網絡可以逼近非線性有理函數的優勢［5］.在對采樣數據進行優化后，利用正則化算法進行圖像重建，并采用6項性能指標對訓練前后的圖像質量進行評價，通過對比訓練前后的重建圖像和性能指標驗證方法的有效性.

1　神經網絡設計

1.1神經網絡結構

在16電極EIT系統中，采用相鄰激勵同步測量的工作模式，一幅圖像需 208（16×13）個邊界電壓.首先，建立包含輸入層、隱含層、輸出層的 208-10-208三層神經網絡模型，如圖 1所示.其中，列向量是神經網絡的輸入；表示輸入層第 i個節點到隱含層第 j個節點的權重值，表示隱含層第j個節點到輸出層第k個節點的權重值，i=1～208，j=1～10，k=1～208，分別表示輸入層、隱含層和輸出層的節點數；列向量是神經網絡的輸出.然后，設置參數和選擇函數.為使輸出數據在 0～1之間，收斂速度快，在隱含層選擇 logsig函數；為使數據能夠按線性輸出，在輸出層選擇purelin函數，訓練函數選擇trainlm函數.

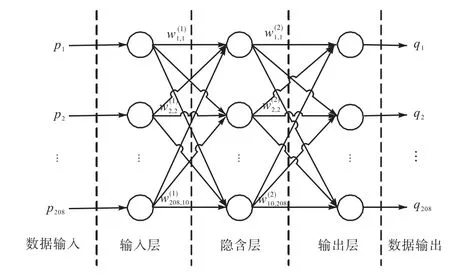
圖1　神經網絡模型Fig.1 Neural network model

1.2神經網絡訓練過程

由于輸入數據的數量級不一樣，同時神經網絡輸出層的激活函數的值域是有限制的，因此需要將神經網絡訓練的目標數據映射到激活函數的值域.首先，在訓練之前要將這些樣本作歸一化處理，歸一化后的樣本數據均在［0，1］范圍內；然后，輸入神經網絡的初始參數和相應函數，對神經網絡進行初始化，初始化后訓練神經網絡.如果訓練后的神經網絡不能達到標準，改變參數和函數，重新訓練網絡；如果神經網絡達到標準，就可以把檢驗組數據輸入神經網絡，得到修正后的成像數據.

2　評價指標

為了更加客觀科學地評價圖像質量，采用6項指標分別對訓練前后的成像效果進行評價［6］.

2.1相關系數

相關系數（correlative coefficient）r用于判斷重建圖像與原始圖像的相關程度，能夠有效地衡量重建圖像的質量，r的取值范圍為［0，1］，圖像相關系數越大，則相關性越強，重建圖像質量越高.

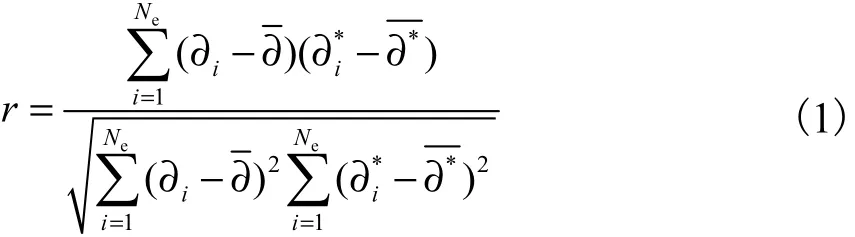
式中：Ne為重建圖像的單元數；表示圖像真實電特性分布；?i表示重建圖像電特性分布分別表示圖像真實值和圖像重建值的平均值.

2.2結構相似度

結構相似度（structural similarity）S表示重建圖像的非線性改變程度，考慮了圖像的亮度和對比度.S的取值范圍為［0，1］，數值越大，成像質量越好.

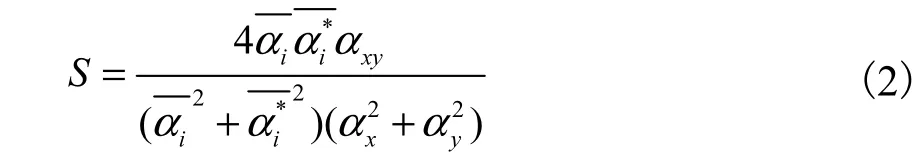
2.3相對誤差

相對誤差（relative error）ER用于衡量重建圖像與原始圖像間的誤差，數值越大，重建圖像質量越低.

式中：β*表示原始圖像真實電特性分布；β表示重建圖像電特性分布.

2.4位置誤差

位置誤差（position error）EP體現了重建圖像真實地表現目標真實位置的程度，EP應該盡可能小，且目標位于不同位置時，EP應能顯示出變化.

式中：rt是的重心到場域中心的距離；rq是的重心到場域中心的距離.

2.5外形形變

外形形變（shape deformation）DS體現了重建目標的形狀偏差程度，DS的值應一致，且足夠小.較大的DS會造成對圖像的分析不正確.

2.6瞬時震蕩

瞬時震蕩（ringing）RNG用于評價重建圖像對于目標區域的異號程度（是否有偽影及偽影程度），RNG是一致的，且足夠小.如果 RNG存在，非導電區域在圖像中會體現為導電區域，造成判斷不正確.

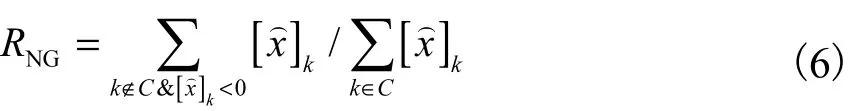
3　實 驗

3.1實驗平臺

利用實驗室搭建的基于 PXI總線的電阻抗斷層成像系統［7］，在空場和4種分布的滿場情況下獲取各100組數據，每組數據包含 208個測量的邊界電壓值；對于每一種分布情況，選擇其中 50組數據作為訓練組，另外 50組作為檢驗組.實驗環境及物理模型如圖2所示.

圖2　基于PXI總線的電阻抗斷層成像系統Fig.2 Electrical impedance tomography system based on PXI bus

實驗中使用 16電極，電極選用金屬鈦圓形點電極，每個電極的直徑為 4，mm，圓形水槽的直徑為20，cm，高為 25，cm，在水槽內盛有電導率為 3.65mS/cm，溫度為25，℃的生理鹽水.在水槽內依次放入1個直徑為5，cm的有機玻璃棒（第二象限），1個直徑為5，cm的有機玻璃棒（第四象限），2個直徑為5，cm的有機玻璃棒（分別為第二、第四象限），2個直徑為5，cm有機玻璃棒（分別為第二、第三象限）和 1個直徑為 4，cm的有機玻璃棒（第四象限）.系統采用電流激勵電壓測量/相鄰激勵同步測量的方式進行數據采集，激勵電流頻率為 100，kHz，幅值為 4，mA，采樣頻率為5，MHz.

3.2神經網絡訓練

利用仿真軟件COMSOL Multiphysics 3.5a建立與實驗系統參數一致的圓形場仿真模型.通過正問題求解，獲得仿真數據，每組數據包含 208個電壓值，將其作為神經網絡的期望值.分別利用空場（電導率分布均勻場）和滿場（電導率分布不均勻場）訓練數據進行訓練，獲得神經網絡的權重值和閾值.以位于第二象限的1個有機玻璃棒為例，訓練結果的數據見表1和表2.其中，b1表示隱含層閾值，b2表示輸出層閾值.經過訓練后，神經網絡（空場）的訓練誤差達到3.6×10-5.神經網絡（滿場）的訓練誤差達到2.5×10-5.

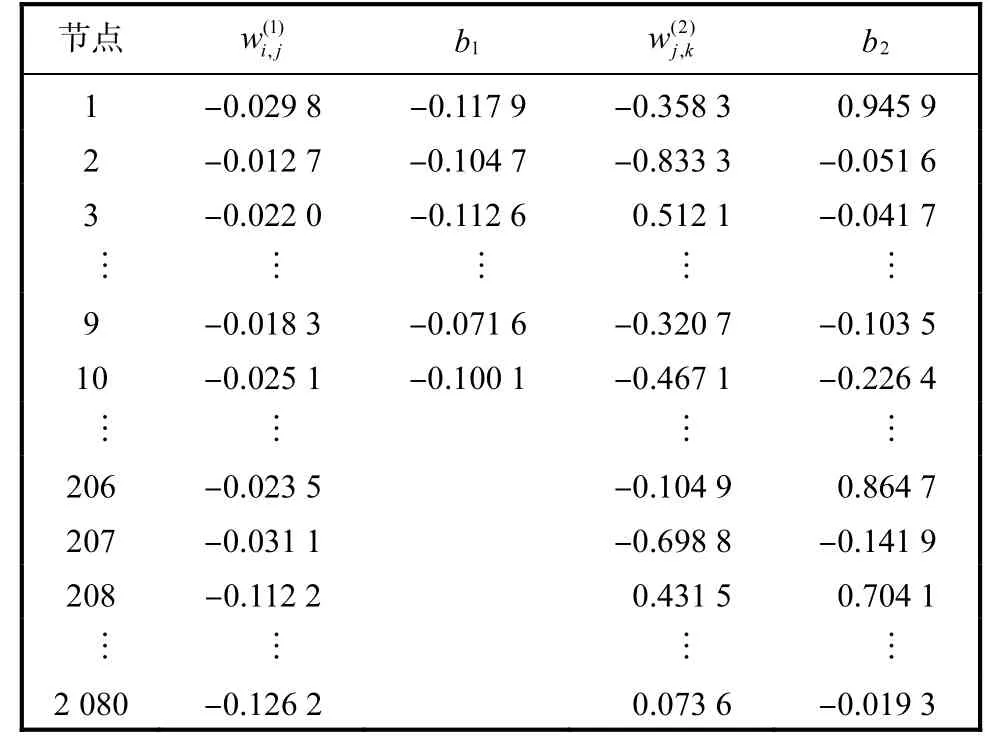
表1　神經網絡（空場）權重值和閾值Tab.1 Neural network weight value and threshold

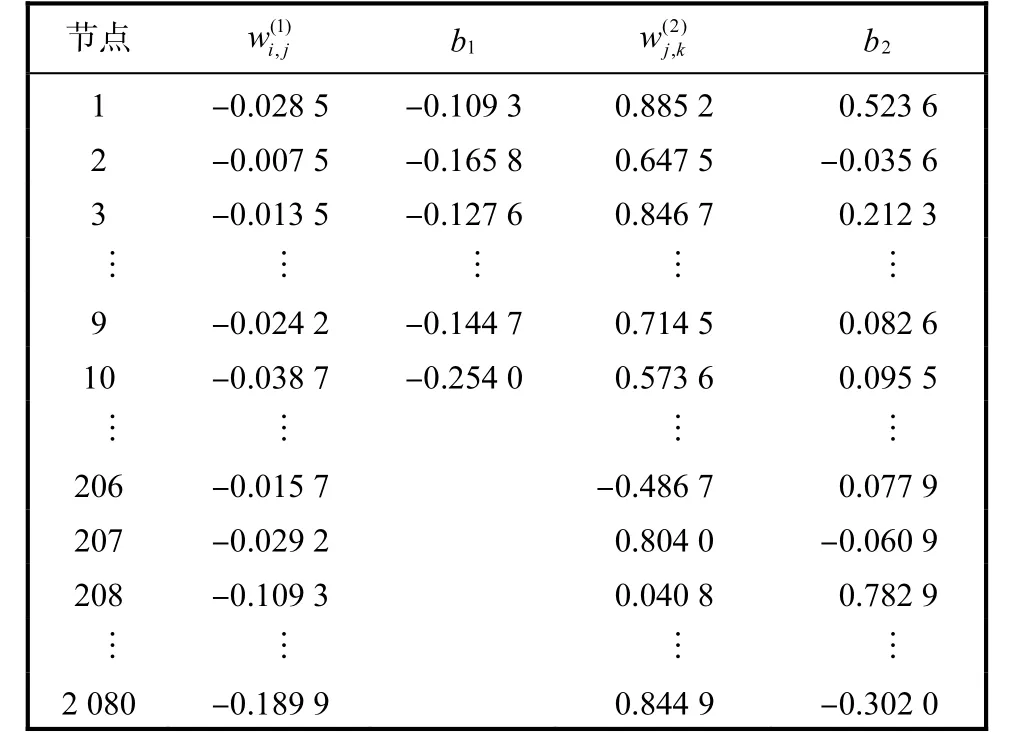
表2　神經網絡（滿場）權重值和閾值Tab.2 Neural network weight value and threshold

3.3重建圖像對比

利用改進的正則化算法進行圖像重建［8］，對場域內4種不同分布分別進行圖像重建，并將經過神經網絡訓練前后的成像效果進行對比，結果見表3.

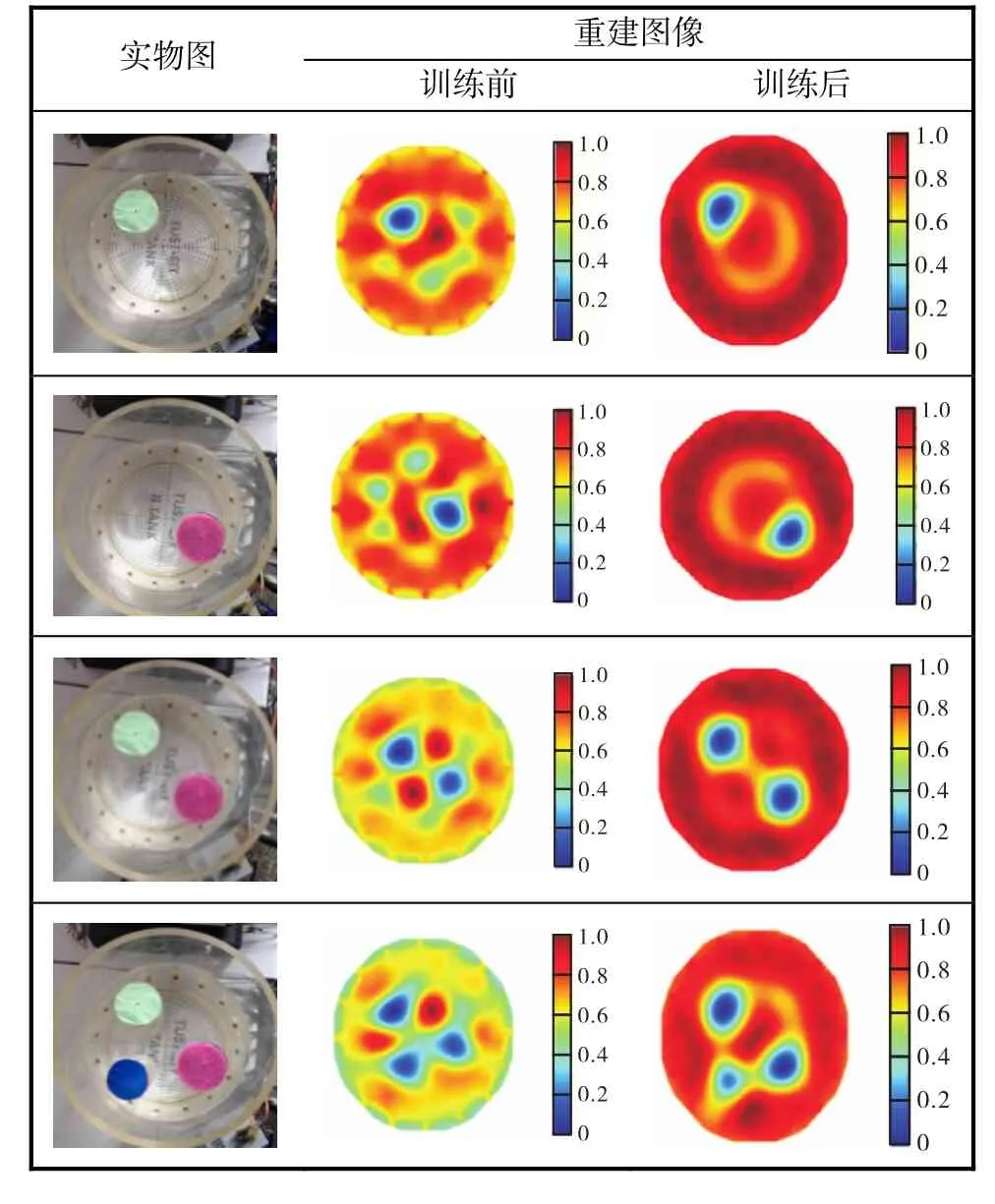
表3　經神經網絡訓練前后的重建圖像對比Tab.3 Comparison of images before and after training with the neural network

由表3可以看出：訓練后的圖像中有機玻璃棒的相對位置和大小都比較準確，形狀圓滑，輪廓清晰，偽影減小，成像效果顯著提高.

3.4評價指標對比

以位于第二象限的1個有機玻璃棒數據為例，訓練前后的 6項性能指標結果見表 4.其中，評價指標提高程度的計算公式為

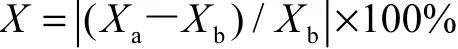
式中：Xa和Xb分別表示訓練后和訓練前r、Ep、S、Ds、ER、RNG的評價指標.

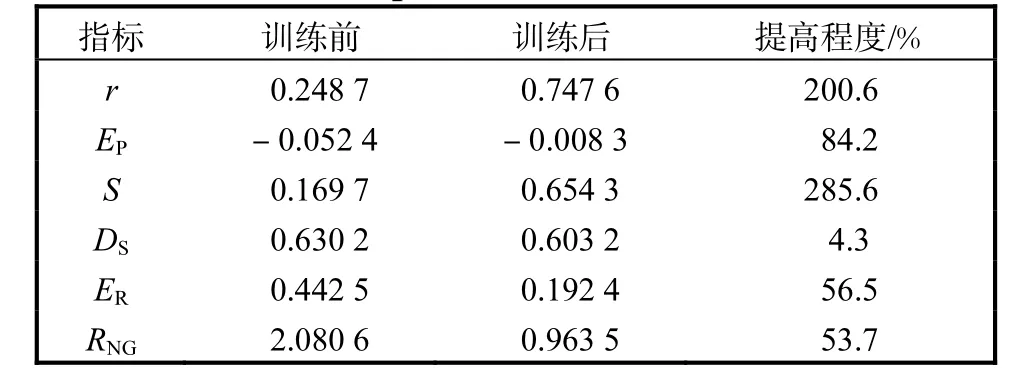
表4　評價指標對比Tab.4 Comparison of evaluation indexes

從表4可以看出：訓練后，圖像相關系數r提高了2倍，位置誤差EP提高了84.2%，，結構相似度S提高了 2.8倍，相對誤差 ER提高了 56.5%，，外形形變DS提高了 4.3%，，瞬時震蕩 RNG提高了 53.7%，指標明顯提高.

4　結 語

本文提出了采用神經網絡提高 EIT成像質量的方法，可以很好地去除圖像的偽影，提高圖像分辨率.在神經網絡參數設計過程中，有些參數比如隱含層的節點數和層數、神經網絡訓練次數，是經過試算和反復實驗得到的，還不夠準確，下一步可以尋找一些適用于 EIT的神經網絡參數經驗公式，從而更科學地計算出神經網絡參數.

由于本文采用仿真數據作為標準組數據，在實際應用中，還可以考慮采用其他測量手段來獲得標準組數據，達到提高成像質量的目的.比如：通過采集大量樣本數據求取平均值作為標準數據，也可以利用CT等成熟的技術獲得標準組數據.此外，本方法僅僅在二維 EIT方面進行了研究，也給三維 EIT圖像質量的改善提供了可能.

本文選用的是有導師監督的神經網絡訓練模式，訓練樣本是來自于相同測量條件下的同一分布.當物場分布發生變化時，建立的神經網絡就不能達到良好的跟蹤效果.下一步將考慮自適應神經網絡的訓練，希望能夠在動態成像過程中，充分發揮神經網絡的數據處理能力，使成像質量達到令人滿意的效果.

［1］ 陸鑫. 基于 LM的電阻抗成像的圖像重建算法［J］. 長江大學學報：自科版，2014，11（34）：52-54.

［2］ Bera T K，Biswas S K，Rajan K，et al. Projection error propagation-based regularization（PEPR）method for resistivity reconstruction in electrical impedance tomography（EIT）［J］. Measurement，2014，49：329-350.

［3］ Michalikova M，Abed R，Prauzek M，et al. Image reconstruction in electrical impedance tomography using neural network［C］//Proceedings of the 7th Cairo International Biomedical Engineering Conference（CIBEC）. Piscataway：IEEE，2014：39-42.

［4］ 謝莉莉，汪鵬，陳麗. PSO算法優化BP神經網絡的EIT圖像重建算法［J］. 制造業自動化，2011，33（2）：45-46，53.

［5］ 張宇博，舒紅平. 改進的 BP神經網絡算法及其應用［J］. 網絡安全技術與應用，2015（3）：78-78，80.

［6］ Adler A，Arnold J H，Bayford R，et al. GREIT：A unified approach to 2D linear EIT reconstruction of lung images［J］. Physiological Measurement，2009，30（6）：S35-S55.

［7］ Chen X Y，Yang T，Yang Y Z. A PXI-based biomedical electrical impedance tomography system［J］. Applied Mechanics and Materials，2014，670：1205-1209.

［8］ 陳曉艷，房曉東. 一種新的正則化圖像重建算法及參數優化［J］. 天津科技大學學報，2014，29（6）：74-77.

責任編輯：常濤

Using Neural Network to Improve the Quality of EIT Imaging

CHEN Xiaoyan，SHI Bo，CHU Mengli，YANG Tao
（College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China）

A method using neural network was proposed to improve the quality of EIT imaging.Firstly，according to the principle of electrical impedance imaging，a three-layer neural network model，208-10-208，was designed.The measured data from the experiment platform were divided into training data and imaging data.The simulation data from the model used as expected value，the neural network model was trained by the training data，and then the parameters of the model were calculated and the neural network was built.Next，the imaging data were put into the trained neural network，and the output data were used to reconstruct images.Finally，six indexes were adopted to compare the effect of the reconstructed images backwards and forwards.The results show that the images’ quality are significantly improved via the six indexes such as the image correlation coefficient，the structural similarity，the relative error，the position error，the shape deformation and the ringing.

neural network；electrical impedance tomography；image reconstruction；image evaluation

TP391.9

A

1672-6510（2016）04-0074-05

10.13364/j.issn.1672-6510.20150096

2015-07-16；

2016-01-25

國家自然科學基金資助項目（61301246）；天津市應用基礎及前沿技術研究計劃資助項目（12JCYBJC19300）

陳曉艷（1973—），女，四川成都人，教授，cxywxr@tust.edu.cn.