Mission-Oriented Configuration Model of Aircraft Carrying Spares and Dynamic Optimization Policy

Ruan Minzhi,Wang Rui,Kong Qingfu

1.Office of Research&Development,Naval University of Engineering,Wuhan 430033,P.R.China;

2.Department of Communication,Dalian Naval Academy,Dalian 116018,P.R.China

Mission-Oriented Configuration Model of Aircraft Carrying Spares and Dynamic Optimization Policy

Ruan Minzhi1*,Wang Rui2,Kong Qingfu1

1.Office of Research&Development,Naval University of Engineering,Wuhan 430033,P.R.China;

2.Department of Communication,Dalian Naval Academy,Dalian 116018,P.R.China

Spare parts are critical to scheduled maintenance and fault repair,and can directly affect the readiness and combat capability of equipment.Equipment′s capacity of carrying spares is influenced by its storage space and scales,so it is necessary to consider economic factors,e.g.spares cost,as well as non-economic ones,such as spares volume,mass and scale,when optimizing spares configuration.Aiming at this problem,the optimization model based on multi-constraints for carrying spares is built by METRIC theory and system analysis.Through the introduction of Lagrange factors,the spares cost is transformed to shadow price,and the optimization method for carrying spares and the dynamic adjustment policy of Lagrange factors are proposed.The result of a given example is analyzed,and demonstrates that the proposed model can be optimized with all constraints,and the research can provide a new way for carrying spares optimization.

carrying spares project;multi-constrains;optimization;Lagrange factors;operational availability

0 Introduction

With the rapid development of military affairs revolution,a large number of new types of weapons and equipments,such as surface warship,long-range strategic missile,fourth-generation fighters,etc,are delivered to combat troops. The issue of combat readiness of weapon system becomes obvious,and the equipment support and equipment operations tend to be equal important. Spare parts are supportability material of planed maintenance and fault repair,and directly affect the equipment life-cycle cost,as well as combat capability[1].When performing combat missions, equipment need to have a strong support capabilities to face the rapidly changing battlefield environment.Therefore,a reasonable planning for carrying spares is critical to improve equipment support ability.

The methods of spares modeling and optimization mainly include single-item modeling,demand oriented modeling,system modeling,availability-centered modeling,and operational readiness based modeling,etc.The basic principle is to meet the precondition of equipment operational availability through cost-effectiveness analysis[2,3].Spares fill rate[4-6],support delay[7]and mission success probability[8]are always used as support effectiveness targets.Through the given target constraints,spares configuration is optimized to minimize the total investment of spares stock.Eor mission-oriented carrying spares support project,several important non-economic factors such as spares mass,volume,quantity, scale,etc,are also need to be considered besides spares stock cost.In the fields of military affairs, such as the naval warship fleets,tank regiment, air squadrons,and orbit space station[9],carrying spares optimization has been widely applied andbecome a worldwide hot spot since the 1990s. Wang,et al.[7]established spares inventory optimization model under multi-constraints,and proposed the method of updated Lagrange to solve the problem.Robert and Bachman,et al.studied the aircraft spares inventory optimization model, and analyzed the relationship between spares mass,volume and backorders[10,11].Wei,et al.[12]constructed a multi-echelon multi-objective optimization model for collaborative supply chain inventory control,and applied genetic algorithm to solve the model.The critical step of optimization model is to determine reasonable constraint factors.During the optimization,values of the factors are repeatedly revised until they meet the given targets when finally the optimal project is obtained[13].

*Corresponding author,E-mail address:ruanminzhi830917@sina.com.

How to cite this article:Ruan Minzhi,Wang Rui,Kong Qingfu.Mission-oriented configuration model of aircraft carrying spares and dynamic optimization policy[J].Trans.Nanjing Univ.Aero.Astro.,2016,33(5):626-632.

http://dx.doi.org/10.16356/j.1005-1120.2016.05.626

We focus on the issue of aircraft spares optimization.Through the introduction of Lagrange factors,the spares mass and volume are transformed to item shadow price,and a new method to solve the problem of spares optimization model under multi-constraints is proposed.

1 Spares Demand Rate

In order to quickly restore the combat effectiveness of failed equipment,the repair mode that replaces the failure items by its spares is usually used[14].In the way,spares demand rate equals to its replacement rate,which is an important input parameter for spares optimization model.The main factors to affect spares demand rate include: equipment reliability,maintenance and repair conditions,repair capacity,equipment task intensity,system structure,equipment deployment and the support organizational structure.The influence factors of spares demand rate and its corresponding model parameters are given in Table 1.

According to spares indenture in system,it is divided to line replaceable unit(LRU)and shop replaceable unit(SRU)[15].Suppose j=1,2,…, J,is the item index of spares,then we can obtain the spares demand rate for LRU

Table 1 Influence factors of spares demand rate

where Djis the duty cycle of item j,Rjrepair in place rate,H0the mean working time(hour)of each week,Zjthe install number of item j in its higher indenture component,N the equipment deployment amount,MTBEjthe mean time between failures of the j th item,and Pjthe retest OK rate for item j.

Eor the item of SRU,suppose SRUkis the subcomponent of LRUj,and its fault isolation probability is defined as qjk,that is,the probability that failure item j is caused by its subassembly k,and then we can obtain the calculation formula of demand rate for SRUk

where Zkis the install number of SRUkin its single parent component LRUj.

2 Configuration Model of Carrying Spares

Suppose the average repair time of item j is Tj,and its spares stock is sj,the expected value E[Xj]and variance Var[Xj]of pipeline of item j are[16]where EBOkis the expected backorders of SRUkand VBOkthe variance of backorders.k∈S(j) means the aggregate of item k which is the subcomponents of LRUj.

Backorders is the state variable of spares stock,recorded as B(X|s),X the amount of spares to be received,and s the spares stock

Expected backorders(EBO)and variance of backorders(VBO)is defined as

EBO=p(X=s+1)+…+k·p(X=s+k)+

where p(X)is the probability distribution of spares to be received.When variance to mean rate Var[X]/E[X]=1,p(X)obeys poisson probability distribution.

If Var[X]/E[X]＞1,p(X)obeys negative binomial distribution[17]

According to the features of negative binomial distribution,its mean value E[X]=ab/(1-b),the variance Var[X]=ab/(1-b)2.If we obtain the value of E[X]and Var[X],the parameters a and b can be determined.

If Var[X]/E[X]＜1,p(X)obeys binomial distribution[18]

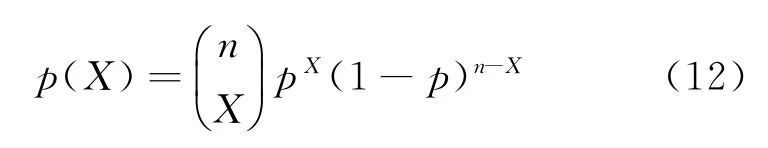
Similarly,for binomial distribution,its mean value E[X]=np,the variance Var[X]= np(1-p),if the value of E[X]and Var[X]are determined,the parameters n and p can be obtained.

Based on the expected backorders of spares, we can calculate the equipment availability,and from different perspectives,it is distinguished as operational availability(Ao),supply availability (As)and inherent availability(Ai).Different definitions about equipment availability are shown as follows,respectively[3]

Eor series system,any shortage of LRU will cause system breakdown,so the spares supply availability is

where MTBE is the mean time between failure, MTTR the mean time to repair,and MLDT the mean logistic delay time.According to Eqs. (13)—(15),we can obtain another formation about operational availability(Ao)

where EBOjis the expected backorders of LRUj, Zjthe install number of item j in its parent component,N the deployment amount of equipment, and j∈I(1)the first indenture item LRUj.

Eor the carrying spares optimization model, the operational availability of system,spares mass and volume need to be considered as the constraints.The basic modeling method is to introduce Lagrange factors based on cost-effectiveness analysis.

where sjis the spares stock,cjthe spares price. Eq.(19)means the constraint of operational availability,where ATis the value of setting target.Eq.(20)means the constraint of spares mass,where mjis the mass of item j,and M0the given target of spares total mass.Eq.(21)means constraint of spares volume,where vjis the volume of item j,and V0the given target value ofspares total volume.

The spares scale is defined as

whereλcis the spares cost factor,γmthe mass factor,andμvthe volume factor.Ifγm=μv=0, there is only factor of cost in the spares scale.If λc,γm,μv≠0,the spares scale includes cost, mass and volume.According Eq.(17),we can obtain its transformation form

where rjis the spares scale of item j,r=(r1,r2,…,rj,…,rJ)the current spares project.After increasing a optimal spares of item j,the new project becomes r′=(r1,r2,…,r′j,…,rJ).Take a logarithm to Eq.(23),we can obtain[19,20]

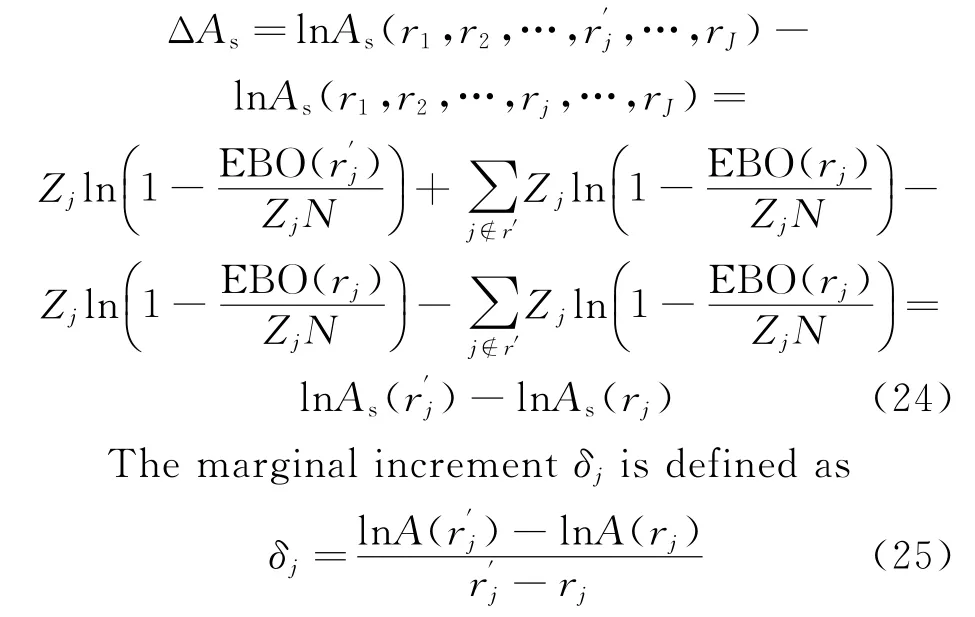
The basic steps of marginal algorithm are shown as follows:

Step 1 Initialize the spares stock,set sj=0.

Step 2 Calculate equipment operational availability,spares volume and mass.

Step 3 Go to the process of optimization, and calculate the marginal incrementδjof each spare.

Step 4 Compared with the marginal incrementδof each spare,the maximum value ofδjis recorded as max(δj),and the optimal spare item corresponding to max(δj)is recorded as j*.Add 1 to the spares stock of item j*,and keep other spares stock unchanged.

Step 5 If the calculation result meets the given targets,the algorithm ends,otherwise,returns to Step 3 and continue to calculate until meeting the given targets.

3 Determination Method and Dynamic Adjustment Policy of Lagrange Factors

The initial values of the Lagrange factors need to be determined before model calculation. The basic method is:

(1)Setγm=μv=0.In this case,only the constraint of spares cost is considered.Through marginal algorithm,we can obtain the optimal result s0=(s1,s2,…,sJ).

(2)Based on the spares configuration s0,we can obtain the spares total cost C(s0),spares mass M(s0)and volume V(s0).

(3)Determine the initial Lagrange factors, γm0=C(s0)/M(s0),μv0=C(s0)/V(s0).Then, we can obtain another spares project,recorded as s,s=(s1,s2,…,sJ).The value ofγm0andμv0 need to be summed up so as to form the penalty factors if the corresponding spares mass or volume exceed the given target.The calculation method of dynamic adjustment forγmandμvis

where M0is the mass constraint target,and V0the volume constraint target.If the current spares project does not meet the constraint,we can update and adjust the value of Lagrange factors through Eqs.(26),(27).

In practice,a special case may appear.No matter how many times we adjust the value of factorsγmandμv,we cannot obtain a solution to satisfy all constraints.In this case,the constraint target should be reset by reducing the value of A0,or increasing M0and V0.

4 Application and Results Analysis

Suppose there is an air force combat unit. Each aircraft of the unit is equiped with an airborne navigation device.Suppose the setting target of operational availability AT＞0.95,R and P for each item equal to 0.Eor airborne navigation device,its mean time to repair MTTR=6 h,andthe mean time between failure MTBE=400 h. According to Eq.(15),we can calculate the inherent availability

Then we can obtain the target of spares supply availability

Spares bill and its parameters are shown in Table 2.Setγm=μv=0,we can obtain a configuration project s0without considering the spares mass and volume.Then,spares supply availability As(s0)=0.968 7,spares cost C(s0)= 3 072 000,spares mass M(s0)=257.7 kg,and spares volume V(s0)=0.411 2 m3.The initial mass factorγm0=C(s0)/M(s0)=1.192,and initial volume factorμv0=C(s0)/V(s0)=747.1.

Table 2 Equipment spares bill and its parameters

Suppose the given target of spares mass M0=250 kg,and spares volume V0=0.4 m3, then,M(s0)=257.7＞M0,and V(s0)=0.411 2＞V0.That is to say,the setting target of spares mass and volume are not satisfied.Based on the initial constraintsγm0andμv0,we can obtain another configuration project s,under which,availability As(s)=0.966 5,spares cost C(s)= 3 091 000,spares mass M(s)=226.1 kg,volume V(s)=0.390 7 m3.Then,A(s)＞As,M(s)＜M0and V(s)＜V0,the result of the project s satisfies the setting constraint targets.

If we change the value ofγmandμv,we can obtain several different spares project,shown in Table 3.Ifγm=μv=0,it is the cost project.If λc=μv=0,it is the mass project.Ifλc=γm=0,it is the volume project.Ifλc≠0,γm≠0 andμv≠0, it is the spares scale project.

Table 3 Optimal spares project under different constraints

The support effectiveness of different spares projects are shown in Table 4,among which,the volume project and scale project satisfy all of the given targets.Eor the scale project,the spares total cost C(R)=3 091 000,which is less than that of the volume project(C(V)=3 782 000), therefore,scale project is optimal solution.

Table 4 Spares support effectiveness for different projects

The result comparisons of support effectiveness are shown in Fig.1,and optimal cost-effectiveness curves of spares project are shown in Fig.2,where the values of cost,mass and volume are normalized.

Fig.1 Support effectiveness for different project

Fig.2 Optimal curves of effectiveness v.s.cost

5 Conclusions

Modeling of carrying spares configuration and its optimization method is researched.The airborne navigation device is taken as example for calculation and simulation analysis.Several conclusions are obtained.

(1)The proposed optimization method is feasible to the application of spares configuration modeling under multi-constraints.Our research conclusions can provide decision-making for spares optimization.

(2)The value of Lagrange factors may affect the calculation result,and is important to multiconstraint modeling.Therefore,reasonable Lagrange factors should be determined.

(3)In the given example,calculation result is reasonable.The spares project satisfies all of the given targets,and can improve the equipment support effectiveness.

Our research is significant for equipment logistics support.It can provide analysis method for spares demand during equipment design,and decision-making for spares configuration optimization and effectiveness evaluation in practice.

Acknowledgements

This work was supported in part by the General Armament Department Pre-research Eoundation in 12th Eive-Year(No.51304010206)and the National Defense Pre-research Project in 13th Eive-Year(No.41404020301).The authors would like to thank the anonymous reviewers for their critical and constructive review of the manuscript.

[1] RUAN Minzhi,LI Qingmin,HUANG Aolin,et al. Inventory control of multi-echelon maintenance supply system under finite repair channel constraint[J]. Acta Aeronautica et Astronautica Sinica,2012,33 (11):2018-2027.

[2] KILPI J,TOYLI J,VEPSALAINEN A.Cooperative strategies for the availability service of repairable aircraft components[J].International Journal of Production Economics,2009,117(2):360-370.

[3] RUAN Minzhi,LUO Yi,LI Hua.Configuration model of partial repairable spares under batch orde-ring policy based on inventory state[J].Chinese Journal of Aeronautics,2014,27(3):558-567.

[4] RUAN Minzhi,LI Qingmin,PENG Yingwu,et al. Model of spare parts fill rate for systems of various structures and optimization method[J].Systems Engineering and Electronics,2011,33(8):1799-1803.

[5] WANG Naichao,KANG Rui.Optimization of multiechelon repairable item inventory systems with fill rate as objective[J].Acta Aeronautica et Astronautica Sinica,2009,30(6):1043-1047.

[6] CAGGIANO K E,JACKSON P L,MUCKSTADT J A,et al.Efficient computation of time-based customer service levels in a multi-item,multi-echelon supply chain:A practical approach for inventory optimization[J].European Journal of Operational Research,2009(199):744-749.

[7] WANG N C,KANG R.An optimization model for inventory spares under multi-constraints and its decomposition algorithm[J].Acta Armanentarii, 2009,30(2):247-251.

[8] WANG Rui,LI Qingmin,RUAN Minzhi,et al.Optimization of repairable spare parts based on combat unit mission success[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(8):1040-1045.

[9] LOO H L,EK P C,SUYAN T,et al.Multi-objective simulation-based evolutionary algorithm for an aircraft spare parts allocation problem[J].European Journal of Operational Research,2008(189):325-341.

[10]ROBERT C K,TOVEY C.Estimating Spare Parts Requirements with Commonality and Redundancy [J].Journal of Spacecraft and Rockets,2007,44 (4):977-984.

[11]BACHMAN T C,KLINE R C.Model for estimating spare parts requirements for future missions:AIAA-2004-5978[R].2004.

[12]WEI Z,XU X E,ZHAN D C,et al.Multi objective optimization model for collaborative multi-echelon inventory control in supply chain[J].Acta Automatica Sinica,2007,33(2):181-187.

[13]IMAN N,SEYED R H.A multi-objective approach to simultaneous determination of spare part numbers and preventive replacement times[J].Applied Mathematical Modeling,2011(35):1157-1166.

[14]YOON K B,SOHN S Y.Einding the optimal CSP inventory level for multi-echelon system in air force using random effects regression model[J].European Journal of Operational Research,2007(180):1076-1085.

[15]RUAN M Z,LI Q M,WANG H J,et al.Application of artificial immune particle swarm optimization algorithm to system-reliability optimization[J].Control Theory&Application,2010,27(9):1253-1258.

[16]WU M C,HSU Y K.Design of BOM configuration for reducing spare parts logistic costs[J].Expert Systems with Applications,2008(34):2417-2423.

[17]WANG N C,KANG R,CHENG H L.Study on the dynamic characteristics of spare inventory based on Markov process[J].Acta Armanentarii,2009,30 (7):984-988.

[18]RUAN Minzhi,LI Qingmin,LI Cheng.Improved layered marginal algorithm to optimize initial spare part configuration project[J].Acta Armamentarii, 2012,33(10):105-111.

[19]DE SMIDT-DESTOMBES K S,VAN DER HEIJDEN M C,VANHARTEN A.Joint optimization of spare part inventory,maintenance frequency and repair capacity for k-out-of-N systems[J].International Journal of Production Economics,2009,118(2): 260-268.

[20]SLEPTCHENKO A,VAN DER HEIJDEN M C, VAN HARTEN A.Effects of finite repair capacity in multi-echelon,multi-indenture service part supply systems[J].International Journal of Production Economics,2002(79):209-230.

Dr.Ruan Minzhi received Ph.D.degree in weapon system and application engineering from Naval University of Engineering in 2012.Currently,he is doing his postdoctoral research at office of research&development,Naval University of Engineering.His research is focused on naval warship equipment logistic support,support resource optimization,equipment support modeling and simulation.

Dr.Wang Rui received Ph.D.degree in communication command from Dalian Naval Academy in 2016.Currently, he is doing his postdoctoral research at development of communication,Dalian Naval Academy.His research is focused on naval warship equipment command automation.

Dr.Kong Qingfu received Ph.D.degree in marine engineering from Naval University of Engineering in 2012. Currently,he is doing his postdoctoral research at office of research&development,Naval University of Engineering. His research is focused on naval warship equipment logistic support.

(Executive Editor:Xu Chengting)

E911 Document code:A Article ID:1005-1120(2016)05-0626-07

(Received 2 July 2015;revised 25 May 2016;accepted 8 August 2016)