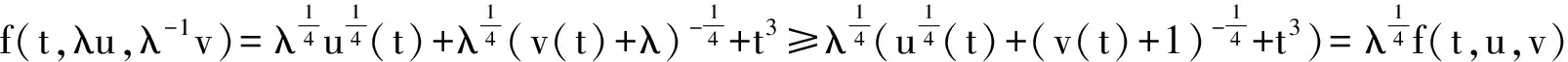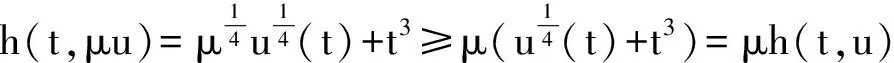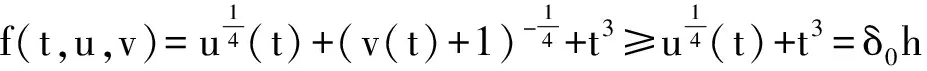帶擾動的梁方程非線性邊值問題正解的唯一性
古傳運,劉 瀏,王園園
(1.四川文理學院數(shù)學學院,四川 達州 635000; 2.達州市經(jīng)濟與信息化委員會, 四川 達州 635000)
?
·基礎(chǔ)學科·
帶擾動的梁方程非線性邊值問題正解的唯一性
古傳運1,劉 瀏1,王園園2
(1.四川文理學院數(shù)學學院,四川 達州 635000; 2.達州市經(jīng)濟與信息化委員會, 四川 達州 635000)
研究一類帶擾動的滑動固定梁方程非線性邊值問題。用混合單調(diào)算子新的不動點定理,得到所研究方程正解的存在唯一性,改進和推廣了前人的工作。舉例應(yīng)用了所得的主要結(jié)果。
梁方程; 非線性邊值問題; 正解; 存在唯一性;混合單調(diào)算子;不動點定理
近年來,利用具有不同邊值條件的四階微分方程模擬彈性梁的彎曲平衡問題已經(jīng)被許多學者所研究,大多數(shù)所考慮的是具有零邊值條件的非線性方程[1-9]。當邊值條件是非零或非線性時,四階微分方程能夠模擬其末端擱在彈性支座上的梁[10-14]。
文獻[12]利用單調(diào)迭代方法研究了一類滑動固定梁方程非線性邊值問題
單調(diào)正解的存在性,其中f∈C([0,1]×R2),g∈C(R)(如圖1所示)。
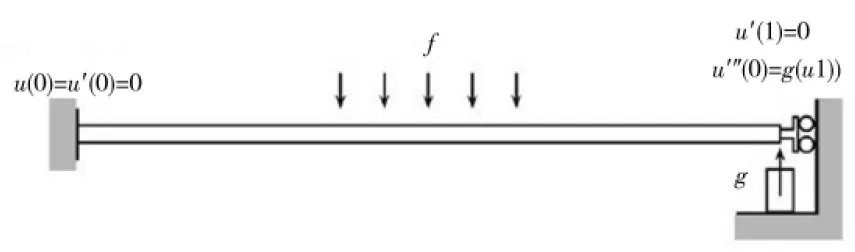
圖1 示意圖
受此啟發(fā),本文將利用帶有擾動的混合單調(diào)算子的不動點定理,研究一類帶擾動的滑動固定梁方程非線性邊值問題
(1)
正解的存在唯一性,其中0 引理 1[12]方程(1)和下面的方程等價: 這里 (2) 和 引理 2 函數(shù)H(t,s)和ψ(t)的性質(zhì)如下: (3) 證明 當0≤s≤t≤1時, 當0≤t≤s≤1時, 當t∈[0,1]時, 假設(shè)(E,‖·‖)是Banach 空間,P是E中的閉凸非空子集,θ是E中的零元素。若P成立(i)x∈P, λ≥0?λx∈P;( ii)x∈P,-x∈P?x=θ,則稱P為E中的一個錐。由P引出E中的半序關(guān)系如下:x,y∈E,x≤y當且僅當y-x∈P。若x≤y且x≠y, 則記作x 記P0={x∈P|x為P的內(nèi)點}, 如果P0非空,則稱錐P為體錐; 若存在常數(shù)N>0,使得對任意x,y∈E,θ≤x≤y,都有‖x‖≤N‖y‖,則稱錐P是正規(guī)的, 其中N叫做錐P的正規(guī)常數(shù)。 任意x,y∈E,若存在λ>0和μ>0,使得λx≤y≤μx,則記作x~y。顯然 ~ 是一個等價關(guān)系。 給定w>θ, 記Pw={x∈E|x~w},易知當?w∈P,有Pw?P且當w∈P0時,Pw=P0。 定義1[15]若?x,y∈E,x≤y,有Ax≤Ay(或Ax≥Ay),則稱算子A:E→E遞增(或遞減)。 定義2[15]若A(x,y)滿足xi,yi(i=1,2)∈P,x1≤x2,y1≥y2有A(x1,y1)≤A(x2,y2),則稱A(x,y)是混合單調(diào)算子。如果A(x*,x*)=x*,稱x*∈P是A的不動點;又若x*>θ,則稱x*是A的正不動點。 定義3[15]A:P→P稱為次齊次算子,如果A滿足 A(tx)≥tA(x),?t∈(0,1),x∈P。 (4) 引理3[15]設(shè)w>θ,β∈(0,1),A:P×P→P是混合單調(diào)算子且滿足 A(tx,t-1y)≥tβA(x,y),?t∈(0,1),x,y∈P , (5) 和B:P→P是次齊次遞增算子。若 (i)有w0∈Pw成立A(w0,w0)∈Pw和Bw0∈Pw, 則: 1)A:Pw×Pw→Pw,B:Pw→Pw; 2)存在u0,v0∈Pw和r∈(0,1)則有 rv0≤u0 3)算子方程A(x,x)+Bx=x在Pw中存在唯一解x*; 4)對任意初值x0,y0∈Pw,構(gòu)造迭代序列 xn=A(xn-1,yn-1)+Bxn-1,yn=A(yn-1,xn-1)+Byn-1,n=1,2,..., 注 1[15]: 若B是零算子, 則引理 3 也成立。 令P={x∈C[0,1]|x(t)≥0,t∈[0,1]},易知P是Banach空間C[0,1]中正規(guī)錐。 斯庫特學會了從別人的角度看問題。她站在拉德利家的前廊上第一次從拉德利家的角度環(huán)顧她再熟悉不過的街區(qū)。真正體會到了父親的話。那一刻,她真正成長了,拉德利不再是怪人,而是那個在寒夜里悄悄為她披上毯子的熱心鄰居。他偷偷縫好了杰姆試圖偷窺他被發(fā)現(xiàn)而不得不丟棄的褲子,雖然針腳歪歪扭扭,他送給孩子們他自己用香皂精心刻成的長得像杰姆和斯庫特的娃娃,一只心愛的懷表,兩枚自己珍藏的古董吉祥幣,還有他最最寶貴的生命。在她眼中,拉德利是一位真正的紳士。 假設(shè): (H3) 存在一個常數(shù)β∈(0,1)使得 f(t,λu,λ-1v)≥λβf(t,u,v),?t∈[0,1],λ∈(0,1),u,v∈[0,) 和 h(t,μu)≥μh(t,u),?t∈[0,1],μ∈(0,1),u∈[0,); (H4) 存在一個常數(shù)δ0>0使得f(t,u,v)≥δ0h(t,u),?t∈[0,1],u,v∈[0,+)。 定理1 若假設(shè)(H1)—(H4)成立,則: 1)存在u0,v0∈Pw和r∈(0,1)使得rvo≤u0 其中,w(t)=t2,t∈[0,1]。 2)問題(1)在Pw中存在唯一正解u*。 3)對任意初值x0,y0∈Pw,能構(gòu)造迭代序列 證明 定義兩個算子A:P×P→E和B:P→E為 由引理1, 易證u是問題(1)的一個解當且僅當u=A(u,u)+Bu,即u是算子A+B的不動點。 由條件(H1), 可知A:P×P→P 和B:P→P。進一步,由條件(H2),可驗證算子A是混合單調(diào)算子和算子B遞增。 另一方面, 對任意λ∈(0,1)和u,v∈P,由(H3)可知 A(λu,λ-1v)(t)= λβA(u,v)(t)。 即對于λ∈(0,1),u,v∈P,有A(λu,λ-1v)≥λβA(u,v),所以算子A滿足條件(5)。同理由(H3)可知,對任意μ∈(0,1)和u∈P, 即對于μ∈(0,1), u∈P,有B(μu)≥μBu,所以算子B是一個次齊次算子。 接下來證明A(w,w)∈Pw和Bw∈Pw, 其中w(t)=t2,t∈[0,1]。 由引理2和條件(H1),(H2),對于?t∈[0,1],則有: 因此,對?t∈[0,1],有 從條件(H1)和(H4),可知 因此有A(w,w)∈Pw。類似可證,對?t∈[0,1],有 易知Bw∈Pw,故引理3的條件(i)滿足。 下面證明引理3的條件(ii) 也滿足。 對?t∈[0,1],u,v∈P,由條件(H4), δ0Bu(t)。. 即,對 ?t∈[0,1],u,v∈P有A(u,v)≥δ0Bu;因此利用引理3可得定理1的結(jié)論。 (I)存在u0,v0∈Pw和r∈(0,1)使得rvo≤u0 其中w(t)=t2,t∈[0,1]; (II)非線性邊值問題 在Pw中存在唯一正解u*; (III)對任意初值x0,y0∈Pw,構(gòu)造一迭代序列 注2:由注1和定理1, 推論易證。 最后舉一例說明定理1。 例 考慮下述非線性邊值問題: (6) 其中g(shù)(u(1))<0。令 再者,我們?nèi)ˇ?=1, 則有 所以(H4)成立。由定理1知,方程(6)在Pw中有唯一正解u*, 其中w(t)=t2,t∈[0,1]。 [1]Daniel F, Donal O, Juan P. Fourth-order Problems with Nonlinear Boundary Conditions [J]. Journal of Computational and Applied Mathematics ,2005, 174:315. [2]Qingliu Yao. Monotonically Iterative Method of Nonlinear Cantilever Beam Equations [J]. Applied Mathematics and Computation, 2008, 205: 432. [3]Xiaoping Zhang. Existence and Iteration of Monotone Positive Solutions for an Elastic Beam Equation with a Corner [J]. Nonlinear Analysis: Real World Applications, 2009, 10:2097. [4]龐彥瓦. 一類四階微分方程邊值問題解的存在唯一性[J]. 長春師范學院學報(自然科學版),2009,28(4):1. [5]Alberto Cabada, Ricardo Roque Engui?a. Positive Solutions of Fourth Order Problems with Clamped Beam Boundary Conditions [J]. Nonlinear Analysis,2011, 74: 3112. [6]王珍燕. 帶2個參數(shù)四階邊值問題的正解及多個正解的存在性[J]. 煙臺大學學報(自然科學與工程版), 2012, 25(1):9. [7]張艷紅. 含有一階導數(shù)的四階邊值問題的正解[J]. 蘇州大學學報(自然科學版),2012, 28(1):7. [8]吳湘云. 一類梁方程邊值問題正解的存在性[J]. 山東科學,2012, 25(5):6. [9]Wang Kun, Yang Zhilin. Positive Solutions for a Fourth-Order Boundary Value Problem [J]. Journal of Mathematic, 2013(8):1. [10]To Fu MA. Positive Solutions for a Beam Equation on a Nonlinear Elastic Foundation [J]. Mathematical and Computer Modelling, 2004, 39: 1195. [11]To Fu Ma, Jair da Silva. Iterative Solutions for a Beam Equation with Nonlinear Boundary Conditions of Third Order [J]. Applied Mathematics and Computation,2004, 159: 11. [12]Edson Alves, To Fu Ma, Maurício Luciano Pelicer. Monotone Positive Solutions for a Fourth Order Equation with Nonlinear Boundary Conditions [J]. Nonlinear Analysis, 2009,71:3834. [13]Li Shunyong , Zhang Xiaoqin. Existence and Uniqueness of Monotone Positive Solutions for an Elastic Beam Equation with Nonlinear Boundary Conditions [J]. Computers and Mathematics with Applications,2012,63: 1355. [14]Mohamed Jleli, Bessem Samet. Existence and Uniqueness of Positive Solutions to a Fourth-order Two-point Boundary-value Problem [J]. Electronic Journal of Differential Equations, 2013(173):1. [15]Zhai C B, Hao M R. Fixed Point Theorems for Mixed Monotone Operators with Perturbation and Applications to Fractional Differential Equation Boundary Value Problems [J]. Nonlinear Anal,2012, 75:2542. (編校:葉超) The Uniqueness of Positive Solutions for Beam Equations with Perturbed Nonlinear Boundary Value Problem GU Chuanyun1, LIU Liu1, WANG Yuanyuan2 (1.School of Mathematics, Sichuan University of Arts and Science, Dazhou 635000 China;2.Dazhou City Provincial Economic and Information Commission, Dazhou 635000 China) This work is concerned with the nonlinear boundary value problem of a class of beam equations with perturbed. Its existence and uniqueness of positive solutions were obtained by using a new fixed point theorem for mixed monotone operators. The result here improves and generalizes the predecessors’ work. Finally, the example was given to illustrate the main result. beam equation; nonlinear boundary value problem; positive solution; existence and uniqueness; mixed monotone operator; fixed point theorem 2015-05-26 四川省教育廳科研項目(14ZB0309);四川文理學院面上項目(2014Z010Y)。 古傳運(1982—),男, 講師,碩士,主要研究方向為非線性泛函分析和微分方程。 O175.8 A 1673-159X(2016)05-0092-6 10.3969/j.issn.1673-159X.2016.05.0171 基本事實和初步結(jié)果

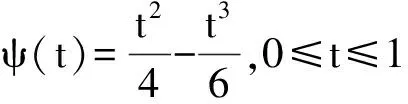
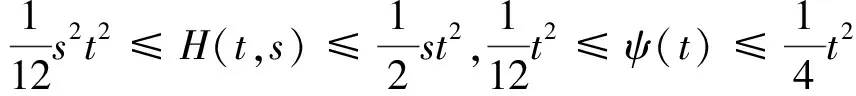
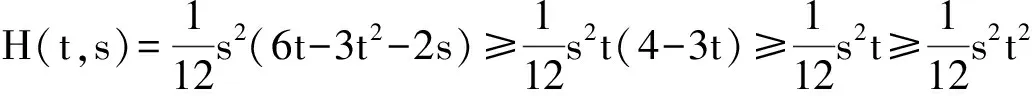
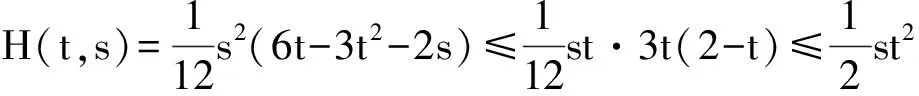
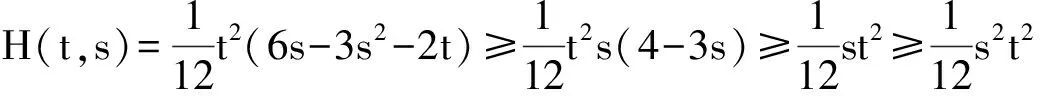
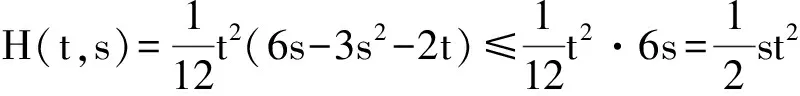
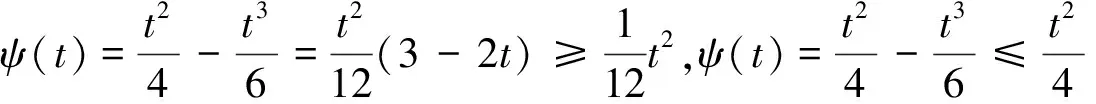
2 主要結(jié)論
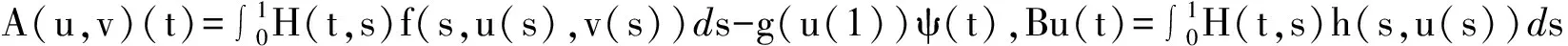
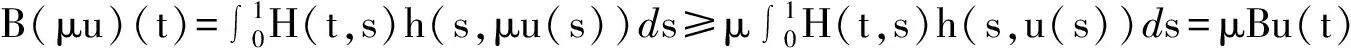
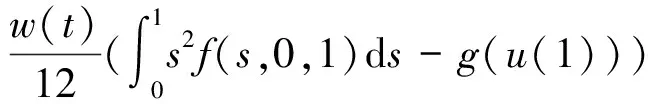
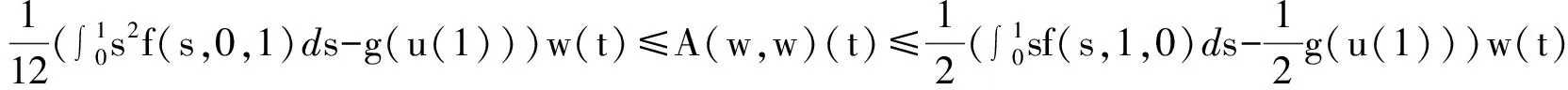
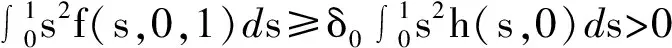
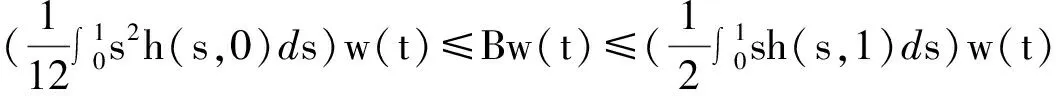
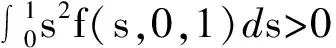
3 應(yīng)用