數學變換在解題中的應用與啟示

(西寧市第二中學 青海西寧 810012)

?

數學變換在解題中的應用與啟示

● 趙小衛

(西寧市第二中學 青海西寧 810012)

在數學里，變換是一個基本概念.例如，平面幾何里常見的合同變換、相似變換還有等積變換，在解析幾何里常用到的坐標變換，線性代數當中的線性變換,仿射幾何里的仿射變換等等.所有這些變換,說到底就是一種映射，其中用變換群來研究對應幾何學的觀點，最早是由德國數學家克萊因提出來的，其意義在于把當時已有的幾何統一在變換群的觀點之下，繼而突出了變換群在幾何中的地位.按照這一背景，在實施數學教學的過程中，通過數學變換的應用與研究有助于我們厘清各種數學對象或者2個數學集合間的內在關系，這樣在認識數學的本質同時也有利于獲得一些重要的數學思想方法.雖然數學變換早已在初中、高中階段得到了廣泛的應用，但對數學變換本身的地位、作用以及不同變換的關系說明得不夠明確，更缺乏系統性，因此適度加強數學變換的教育意識有助于我們了解更多有關數學的本質特征.下面筆者借《數學通報》2013年第8期中的2 137號征解題作為線索談一談數學變換的思想作用，請大家予以賜教.

問題 在△ABC中，分別過點A,B作它的外接圓的切線相交于點P，聯結PC交圓于點D，交AB于點E，求證:

代數不過是書寫的幾何，而幾何不過是圖形的代數——索菲婭·格梅茵.由此出發可以先作圖與式的變換：

圖1

證法1 如圖1，分別以直線PO,AB為x軸、y軸建立平面直角坐標系.設P(a，0)，直線PC的傾角為α，則直線PC的參數方程為：

另設圓心為O′(k，0)，⊙O′的半徑為r,則⊙O′的方程為

(x-k)2+y2=r2.

將直線PC的參數方程代入圓方程得

(a+tcosα)2-2k(a+tcosα)+k2+t2sin2α=r2,

化簡得

t2+2(a-k)tcosα+(k-a)2-r2=0,

于是

t1+t2=-2(a-k)cosα,

t1t2=(k-a)2-r2,

又在Rt△PAO′中，根據勾股定理得

PA2=O′P2-O′A2=(k-a)2-r2,

按照射影定理可得

PA2=PO·PO′=|a|(k-a),

故

從而

即

得

亦即

PD·EC=DE·PC，

故

因此

圖2

證法2 以點P為極點、射線PO為極軸建立極坐標系.設O′(m,0)，⊙O′的半徑為r，射線PC的方程為θ=φ，∠PO′A=β,則AB的方程為

ρcosθ=m-r·cosβ,

于是

故

又⊙O′的方程為

ρ2-2ρm·cosθ+m2-r2=0,

因此

即

從而

亦即

PD·EC=DE·PC,

故

因此

評注 證法2實際上是依據直角坐標與極坐標間的對應關系，把證法1中直角坐標形式下的坐標和方程分別轉變成了極坐標形式下的坐標和方程，并通過這一形式上的變換得到了用極坐標同樣可解的方法.它體現的是一種以對應為基礎的數學變換關系——坐標變換.這里2個坐標系間的坐標變換關系為：x=a+ρ·cosθ,y=ρ·sinθ,k=m+a.

圖3

證法3 如圖3，作PC關于PO′的對稱圖形PC′,交⊙O′于點D′,C′,交AB于點E′,聯結D′E,EC′,DE′,DC′，則

PC·PE+PD·PE=

PE·PC′+PD·PE′,

PC·PD=PD·PC′,

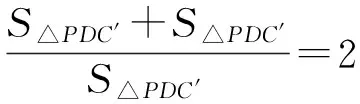
故

因此

即

亦即

PD·EC=DE·PC,

故

因此

評注 證法3是把在同一直線上的4條線段PD,PC,EC和DE利用平面幾何中的軸對稱變換分散到2條直線上，然后再利用面積法對問題給予證明的方法.這里所采用的軸對稱變換實際上是合同變換中的一種，所謂合同變換亦稱全等變換或正交變換，其形狀和大小完全相同的圖形就叫合同形，合同變換主要含平移變換、旋轉變換以及軸對稱變換.

凡此種種，引發我們的思考：究竟什么才是數學的本質？數學解題除了邏輯以外的部分又是什么？所有的這些問題或許只有透過各種不同的數學變換才能讓人們找到數學的神韻和真諦.實際教學中又該怎樣通過數學變換把各部分內容有機地整合在一起，還需要進一步實踐和探索.