數形結合思想方法在數學教學中的應用分析

蔡冬蓮（湖南省益陽市益師藝術實驗學校，湖南 益陽413000）

數形結合思想方法在數學教學中的應用分析

蔡冬蓮（湖南省益陽市益師藝術實驗學校，湖南 益陽413000）

現在，數學思想方法的教學已經得到了社會的認可，得到了應有的重視。數形結合滲透在數學知識之中，是初中數學解題中一種重要的數學思想方法，在數學領域中應用甚廣。數形結合將數和形完美的結合在一起，貫穿了初中數學的兩大主線-數和形。縱觀整個數學教材，有許許多多的知識都體現數形結合的思想。在初中教學中，應用數形結合的思想方法，有助于學生解題思路的拓展和數學思維的發展。本文主要對數形結合的意義以及數形結合在教學中的應用進行了詳細的分析。

初中數學；數形結合；教學；應用

1 引言

數學是研究數量關系和空間形式的一門學科，是刻畫社會規律和自然規律的有效工具和科學語言。為了適應時代的發展，每個公民都必須具有較強的數學知識，數學教學不僅要讓學生掌握必需的數學知識，還應該提高學生的數學能力，數學的思想方法將兩者連接起來。數形結合是利用數與形之間的對應關系，在數與形之間相互轉化，使抽象問題具體化，復雜問題簡單化，最終簡化問題的一種數學思想方法。

2 數形結合思想在數學教學中的地位和意義

2.1 數形結合在初中教學中的地位

數形結合在數學教學中具有非常重要的地位，具有整合性強、解法靈活的優點，可以對學生的創新能力、實踐能力和思維能力加以考察，它將函數、方程、不等式等代數知識與多邊形、數軸、圓等幾何知識聯系在一起，在數學教學中運用數形結合的思想，不僅能夠幫助學生系統的掌握數學的概念，對學生思維能力的發展也有重要的作用。

2.2 數形結合在數學教學中的意義

數形結合不僅能夠使概念完整化，解題問題具體化，使學生主動學習，不僅能夠幫助學生理解各種公式，還能幫助學生盡快的解決問題。

2.2.1 學生對數學進行認知的基礎是數學概念

數學概念被認為是數學這門學科的邏輯起點。數學概念是對知識的高度濃縮，是經過多次抽象的結果，其最大的特點就是僅僅應用文字表達相應的結論。數學本身具有抽象性，往往被人們看作是枯燥、難懂的學科。數形結合的思想方法就是對數學概念從“數”和“形”兩方面進行表述，從本質上揭示數學知識，從而讓學生不再僅僅理解和記憶概念的表面文字，而是對概念進行本質的理解。

2.2.2 有助于提高解題能力

學習數學知識就是為了應用學到的知識解決具體的數學問題，數學知識的掌握情況是影響數學問題解決能力的主要因素，而數學思想方法的掌握和應用情況也或多或少的影響著數學解題的能力。數學思想方法的一種重要方法就是數形結合，對其的掌握能夠幫助學生盡快找到解題的途徑，進而提高學生的解題能力。

數形結合就是根據對象的數形將數和形巧妙的結合在一起，解決問題的關鍵所在就是在數和形之間相互轉化，在研究圖形時，利用代數的性質，解決幾何的問題。在解決代數問題時，想到它的圖形，進而找到解題的思路。實現抽象問題與具體形象的相互聯系和轉化，化抽象為具體，化難為易，使問題簡單化。

2.2.3 數形結合有助于學生全方位、多角度的思考問題

在數學教學中，數形結合思想能夠培養學生的想象力和創造力。在初中課本當中，大部分的章節都出現了思考、探究、練習、復習鞏固等問題，在課堂教學當中應該創設情境，激發學生急于求知的好奇心，引發學生求知的欲望。

3 數形結合思想方法在數學教學中的應用

3.1 數結合形的思想方法

數學具有高度的抽象性，為了能夠使問題具體化，就必須運用數形結合的思想，可以把抽象不易解釋的數與直觀形象的形結合在一起，使數在形的幫助下促使學生理解接受數。例如，虛數就是由于找到了幾何解釋才在數學中站穩了腳跟，從而成為了有關復數的數學分支。加強學生對數形結合思想的培養，可以有效的提高學生分析問題和解決問題的能力。

例1：在推導單項式乘法、單項式與多項式的乘法以及多項式的運算法則時，借助于圖形表示就可以讓學生更好的接受。比如，求3a×4a的值時，可以將4a作為一個長方形的長，3a作為長方形的寬，那么長方形的面積就可以用3a×4a表示，如圖1所示。

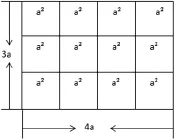
圖1

于是有3a×4a=12a2，通過進一步的分析概括就可以得到單項式乘法的運算法則。

對于推導多項式與單項式的乘法法則以及多項式的乘法的法則使均可作類似的設計。

例2設a＞0，b＜0，且∣a∣＜∣b∣。①用“＜”連接a、-a、b、-b；②用“＞”或“＜”號填空，a-b_0，-ab_0，1/a_1/b。

分析：這種類型的題如果一拿到題就考慮有理數的性質，容易搞亂學生的思維，使得學生難得其解。如果換種角度，借助于數軸分析，這個問題就變得清晰、明了。

圖2

由題設得數軸。

學生就會很容易的看出：

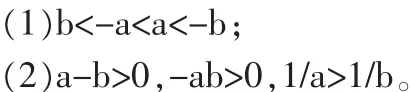
3.2 以數解形

“以數解形”，就是利用“數”的精確性揭示出“形”中蘊含的數量關系，形雖然直觀具體，簡單明了，但是缺乏數的精準，形結合數的思想方法使得直觀的形與準確的數結合在一起，使得形在數的幫助下得到了新的發展和新的面貌。下面通過舉例來說明用數的方法解決形的問題。

例3：已知：如圖3，圓O內切于三角形ABC，其中AB=9，AC=11，BC=13。求：過三角形ABC的各個頂點的切線長。

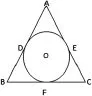
圖3

分析：觀察圖形，過三角形ABC三個頂點的切線分為為AD和AE，BD和BF，CE和CF，且AD=AE，BD=BF，CE=CF。已知條件中給出了三角形三條邊的長度，這時可以想到，將三角形ABC的三條邊均拆成某兩條線段的和，然后化成方程組問題進行求解。

解：如圖3。

設圓O與三角形ABC三條邊分別相切于點D、E、F，設AD=x，BD=y，CF=z，則有：

所以過三角形ABC的頂點A、B、C的切線分別為5、4、9。

例4：如圖4，矩形ABCD中，AB=5，AD=8，在AB、AD上各取點Q、P，使QP=3，求五邊形PQBCD面積的最小值。

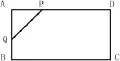
圖4

分析：要想做到五邊形PQBCD面積的最小值，只要求出三角形APQ面積的最大值，令AP=X，AQ=y，則：

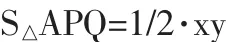
注意到x2+y2=32，那么這個問題就可以轉換為代數問題：在x2+y2=32的條件下，求1/2·xy的最小值。

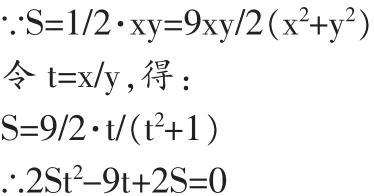
由于上式作為關于t的一元二次方程有實根，故△=81-4（2S）（2S）≥0

∴△S≤9/4∴APQ面積的最大值為9/4，

4 數形結合思想的培養

4.1 在數學概念教學中培養數形結合思想

在平時的課堂教學中，為了加深對概念的理解，應該把直觀的模型或圖形帶到課堂教學當中，在課堂上老師和學生相互交流，總結出具體圖形及數量之間的關系。老師要引導學生要從實際生活出發，充分發揮數學和生活的聯系，在日常生活中學生聯系實際，找到解題的方法，深刻體會數學在生活中的實際價值。

4.2 在數學練習題中培養數形結合思想

在講解具體的數學習題時，應該引導學生在無形當中找到習題中所包含的數學方法和數學思想，而不是過分強調解題的速度，直接把正確的思維告訴學生。學生在做數學習題時，要鼓勵他們積極探索數形結合的思想，根據題干找到問題的所在，找到解題的方法，最后自主的完成習題的解答。學生經歷這個過程之后對數學知識的理解就會加深。

5 結束語

所有的事物都是由數和形兩方面組成的，數和形的結合一定存在于方方面面當中。數形結合作為一種思想方法，蘊含、滲透在數學知識當中。它是以數學知識為基礎，將數量關系和空間形勢結合在一起，利用數和形的優勢互補去解決各種各樣的問題。在中學階段在解決問題時數形結合思想起到了非常關鍵的作用，數學結合可以使學生學習主動化，使問題簡單化，概念形象化。由此可見，數形結合是數學思想方法的核心，在數學中有著不可替代的作用。我們每個老師在平時的教學當中應該有意的滲透數形結合的思想，并不斷思考滲透的策略，提高教學的方法。

[1]高愛紅.數形結合思想在初中數學教學中的應用研究[J].數學教學通訊，2016（01）：45～46.

[2]教育部.義務教育教學課程標準[S].北京師范大學出版社，2011.

[3]劉桂玲.數形結合思想方法在高中數學教學中的應用分析[J].中國校外教育，2015（08）：24～25.

G633.6

A

2095-2066（2016）22-0273-02

2016-6-3

蔡冬蓮（1975-），女，中學一級教師，本科，主要從事中學數學教育工作。