非零初始條件線性系統的Legendre多項式模型降階方法

宋秋艷,宋述剛

(長江大學信息與數學學院，湖北 荊州 434023)

?

非零初始條件線性系統的Legendre多項式模型降階方法

宋秋艷,宋述剛

(長江大學信息與數學學院，湖北 荊州 434023)

討論了非零初始條件下線性系統的模型降階問題，并給出了一種基于Legendre正交多項式的時間域模型降階算法。該方法首先將系統的狀態變量在正交多項式空間中進行展開，然后由狀態方程得到展開系數的簡單遞推式，接著對其正交化，求得投影矩陣，通過正交投影變換得到降階系統。由該方法得到的降階系統可以匹配原始系統輸出變量一定數量的正交多項式展開系數，從而保證了降階的精度。最后，通過2個數值算例驗證了該算法的有效性。

模型降階；Legendre多項式；投影方法

模型降階這一思想到現在已有40多年的歷史。簡而言之，模型降階就是在某種情況下將一個較大的復雜系統轉化為一個近似的較小系統的過程。模型降階是一種有效的降低動力系統復雜性的技術。該類技術能夠減少數據的存儲量和運算量，降低大型復雜系統的理論分析難度，加速系統的模擬計算，同時在一定的誤差范圍內保持系統的某些重要屬性。模型降階方法已被成功地應用于許多工程應用領域和其他學科的分支中，如大規模集成電路模擬、自動化控制和機械工程等[1～3]。自模型降階方法被提出以來，已經發展出多種方法，其中最主要的2類分別是Krylov子空間類方法和基于奇異值分解的平衡截斷模型降價方法。

Krylov子空間方法是投影類模型降階方法，該類方法數值穩定，算法實現簡單，并且計算量較小，受到很多科技工作者的青睞，但其沒有比較理想的誤差估計結果；平衡截斷模型降階方法可以直接得到降階模型的誤差估計結果，并能保持系統的穩定性，但是該類方法在降階過程中需要求解大規模的Lyapunov方程，運算量較大，計算復雜度比較高，制約其應用的廣泛性。近些年來，由平衡截斷方法與投影類方法結合形成新型模型降階方法成為研究熱點之一。

近年來，基于正交多項式(包括Chebyshev正交多項式、Legendre正交多項式和Laguerre正交多項式等)的模型降階方法也受到了廣泛的關注。這類算法的核心思想是首先將系統的狀態變量在以正交多項式為基底的空間中進行展開，然后由系統的狀態方程求得狀態變量的多項式展開系數，最后通過該展開系數構造標準列正交矩陣對原始系統進行降階。由此得到的降階系統一般都能夠匹配原始系統的輸出函數在正交多項式張成的空間中一定數量的展開系數。該類方法是一種時間域模型降階方法，已被成功地應用于線性系統、非線性系統以及一些特殊結構系統的模型降階中[4～7]。

傳統的模型降階方法，在降階過程中一般都只考慮系統的輸入輸出性態，忽略初始條件的影響，或者為了簡便假設初始條件為零，這樣，使得原始系統的初始信息遭到破壞，給降階系統帶來不可預測的結果[8, 9]。因此，傳統的模型降階方法對非零初始條件的系統一般不太適用。基于此，筆者針對非零初始條件的線性系統，提出一種基于Legendre正交多項式的時間域模型降階方法。

1 Legendre正交多項式

定義1 多項式:

稱為Legendre多項式。

性質1 Legendre多項式在區間[-1,1]上滿足如下正交性：

性質2 對Legendre多項式，遞推公式(1)成立：

(1)

其中, P0(t)=1,P1(t)=t。

Legendre多項式Pi(t)可以展開為如下的冪級數:

(2)

式中, fij為冪級數tj的展開系數。

將式(2)帶入式(1)，可得:

(3)

比較式(3)兩邊關于t的各次冪的系數，可得：

任意一個可積函數x(t)均可以在Legendre正交多項式基底下近似展開：

(4)

由文獻[10] 可知，可測函數的正交多項式展開在Lebesgue意義下是一致收斂的，且正交多項式的近似展開在最小平方誤差意義下是最優的，因此，相對低價的正交多項式近似可以達到較高的精度。

可以將最小二乘法與Legendre正交多項式相結合來計算函數x(t)的冪級數展開系數xi。將式(2)代入到(4)中，比較兩邊t的各次冪的系數，有:

其中, αj的值可由Legendre多項式的正交性求得:

在實際應用中，可以用文獻[11] 中復雜度為O(NlogN)的快速算法來計算函數x(t)的前N個Legendre正交多項式展開系數。

2 基本算法

下面，筆者將給出非零初始條件下線性系統的基于Legendre正交多項式的模型降階方法的具體過程。

考慮如下單輸入單輸出線性系統：

(5)

其中, A∈Rn×n;b,c∈Rn;x(t)∈Rn為系統的狀態變量; u(t),y(t)∈R分別是系統的輸入變量和輸出變量;n為系統的維數。

為得到原始系統(5)的降階系統，首先將系統的狀態變量x(t)和輸入變量u(t)近似展開為：

(6)

(7)

其中,hi∈Rn,ui∈R分別為x(t)和u(t)的展開系數向量。

將式(6)和(7)代入式(5)，有:

整理得:

比較兩端常數項和ti(i=1,2,…,r-2)所對應的系數，并忽略高階項tr-1，最終可得:

(8)

式中,h0為給定的初始條件x0。

由遞推式(8)便可求得狀態變量x(t)的展開系數向量hi(i=1,2,…,r-1)。

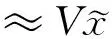
(9)

3 數值算例

下面，筆者通過2個數值算例來驗證上述模型降階方法的有效性。

例1 考察一個實際的大氣風暴軌跡的地球大氣模型[3]，由形如系統(5)的598階微分動力系統來描述，其初始條件為x0=[0,0,…,0,1]T。

對該系統采用基于Legendre正交多項式的模型降階方法降至16階，原始系統與降階系統關于輸入函數u(t)=e-0.5tsin10t的瞬態響應及其相應的誤差如圖1、圖2所示。

圖1 例1的瞬態響應

圖2 例1中降階模型的相對誤差

例2 考慮形如系統(5)的1006階微分動力系統[3]，其中:

A=diag{A1,A2,A3,A4}

A3=diag{-1,-2,…,-1000}

對該系統采用基于Legendre正交多項式的模型降階方法降至20階，原始系統與降階系統關于輸入函數u(t)=sint的瞬態響應及其相應的誤差如圖3、圖4所示。

圖3 例2的瞬態響應

圖4 例2中降階系統的絕對誤差

由以上2個數值算例的模擬結果可以看出，基于Legendre正交多項式的模型降階方法得到的低階模型對原始模型有很好的近似效果。由于考慮了初始條件，該方法對于非零初始條件的線性系統是有效的。

4 結語

傳統的模型降階方法往往忽略初始條件，使得降階模型的精度無法保證。針對帶非零初始條件的線性系統，提出了一種基于Legendre正交多項式的模型降階方法。該方法不僅考慮了初始條件，并且降階過程簡單高效，數值算例驗證了該方法的有效性。基于正交多項式的模型降階方法是一類時間域的模型降階方法，該類方法一般與系統的輸入函數有關，如何削弱該類方法對輸入函數的依賴性，擴展其應用是值得進一步研究的問題。

[1]蔣耀林. 模型降階方法[M]. 北京: 科學出版社, 2010.

[2]Antoulas A C. Approximation of Large-Scale Dynamical Systems[M].Philadelphia:SIAM,2005.

[3]Benner P, Mehrmann V, Sorensen D C. Dimension Reduction ofLarge-Scale Systems[M]. Springer-Verlag Berlin Heidelberg, 2005.

[4]Wang J M, Chu C C, Yu Q J, et al. On projection-based algorithms formodel-order reduction of interconnects[J]. IEEE Trans Circuits Syst Regul Pap, 2002, 49(11): 1563～1585.

[5]Jiang Y L, Chen H B. Time domain model order reduction of generalorthogonal polynomials for linear input-output systems[J]. IEEE Trans Autom Control, 2012, 57(2): 330～343.

[6]Jiang YL, Chen H B. Application of general orthogonal polynomials tofast simulation of nonlinear descriptor systems throughpiecewise-linear approximation[J]. IEEE Trans Comput Aided Des Integr Circuits Syst, 2012, 31(5): 804～808.

[7]Xiao Z H, Jiang Y L. Model order reduction of MIMO bilinear systems by multi-order Arnoldi method[J]. Syst Control Lett, 2016, 94: 1～10.

[8] Heinkenschloss M, Reis T, Antoulas A C. Balanced truncation model reduction for systems with inhomogeneous initial conditions[J]. Automatica, 2011, 47(3): 559～564.

[9] Shen J, Lam J. model reduction for discrete-time positive systems with inhomogeneous initial conditions[J]. Int J Robust Nonlin, 2015, 25(1): 88～102.

[10] Szego G. Orthogonal polynomials[M]. New York city: American Mathematical Society, 1939.

[11] Iserles A. A fast and simple algorithm for the computation ofLegendre coefficients[J]. Numer Math, 2011, 117(3): 529～553.

[編輯] 洪云飛

2016-06-26

國家自然科學基金項目(11201039)。

宋秋艷(1989-)，女，碩士生，現主要從事應用數學方面的研究工作；通信作者：宋述剛，教授，2712281782@qq.com。

O231

A

1673-1409(2016)28-0001-05

[引著格式]宋秋艷,宋述剛.非零初始條件線性系統的Legendre多項式模型降階方法[J].長江大學學報(自科版)，2016,13(28)：1～5.