基于禁忌搜索優化的直線進給系統矢量控制

林 健，劉 坤，施昕昕，劉 娣

(南京工程學院 自動化學院 ，南京 211167)

?

基于禁忌搜索優化的直線進給系統矢量控制

林 健，劉 坤，施昕昕，劉 娣

(南京工程學院 自動化學院 ，南京 211167)

數控機床的直線進給矢量控制系統中包含多個PID調節器，其控制參數直接影響系統性能。而直線進給系統是一個復雜的非線性時變系統，為了優化PID調節器控制參數，文章提出了改進的禁忌優化算法(Tabu)，并將其應用于直線進給系統。在分析現有禁忌算法基礎上，對Tabu算法的鄰域范圍、Tabu表和算法終止條件進行了改進，以直線進給系統的跟蹤性能指標為目標函數, 應用該算法對直線進給矢量控制系統各調節器的PID參數進行優化，并進行了實驗驗證。結果表明，應用文中方法優化控制器參數后，與傳統PID控制相比，直線進給系統在負載改變時轉速波動和位置跟蹤誤差顯著減小，提高了直線進給系統的穩態和動態性能。

直線進給系統；禁忌搜索；矢量控制；PID參數優化

0 引言

在高性能數控機床中，除了要有性能優良的高速主軸單元外，還需要有剛度高，動態響應迅速的快速進給系統。傳統的“旋轉伺服電動機+滾珠絲杠”傳動方式所能達到的最大速度與加速度有限，遠遠不能滿足生產的需求。直線電動機驅動的進給系統取消了從電動機到工作臺之間的一切中間傳動環節，其速度可以達到滾軸絲桿副的30倍，加速度可達滾軸絲桿副的10倍，且頻率響應高，因此被越來越多地應用于高速精密機床中。但直線進給系統是高剛度、高加速度系統，“零傳動”使得在工作過程中各種自身和外界擾動都直接作用在直線電動機上，且直線電動機由于其獨特的結構產生端部效應，引起推力波動，這些特點使得其控制難度增加[1-3]。矢量控制方案是目前直線進給控制系統的主要控制方式之一， 其控制效果的好壞與各調節器PID參數的配置密切相關。工程上根據實驗和經驗整定PID參數的方法很多，然而都存在參數整定困難、整定結果性能不高等問題。韓京清設計一種跟蹤微分器來實現系統的無超調控制，但參數條件過于復雜[4]。黃科元等采用輸出微分負反饋來消除超調，然而輸出微分會引入噪聲，影響系統性能[5]。直線進給系統是一典型的非線性多變量耦合系統，端部效應、負載阻力擾動、摩擦力擾動、推力擾動、磁鏈諧波擾動等多種擾動對系統的性能都會造成明顯的影響，對于這樣一個非線性、時變、大延時的復雜系統，其PID 參數整定實質是一個優化問題，即在可行域內迅速找到全局最優解，現在越來越多地應用到智能優化方法，包括模糊控制、神經網絡、粒子群算法、遺傳算法等，這些方法不依賴于系統數學模型，將這些智能算法用于整定PID 調節器，可有效提高控制器的魯棒性和控制精度。藍益鵬將模糊PID 控制器應用到直線電機懸浮子系統位移環中，以滿足懸浮系統控制高精度的要求，然而模糊控制中模糊規則的設計完全依賴于經驗[6]；韓明文用RBF神經網絡整定PID來控制直線電機，在一定程度上改進了傳統PID 控制性能，但神經網絡結構復雜，控制難度大[7]；盤真保采用遺傳算法對直線電機二自由度PID 控制器的參數進行優化，解決傳統控制器在設定值跟隨性能和干擾抑制特性不能達到共優的問題，但遺傳算法迭代次數多、計算效率低[8]。禁忌算法(Tabu)作為一種高效啟發式算法受到越來越多的關注[9-11]， 具有收斂速度快、搜索精 度高的優點，本文的主要工作有三個方面：①首次將Tabu算法應用于直線電機矢量控制系統中PID 參數的整定；②為了提高Tabu算法的收斂精度與搜索速度，對算法的鄰域范圍、Tabu表和算法終止條件進行了改進；③在自制控制器的實驗平臺上進行了實驗，得到Tabu優化后的控制器在不同擾動下的速度跟蹤曲線以及階躍輸入下的位置跟蹤曲線，并與傳統PI控制器跟隨性能進行比較，驗證了算法的有效性。

1 直線進給系統的矢量控制

將正弦三相對稱交流電通入直線電動機動子繞組中后，如果不考慮縱向端部效應，會產生沿展開方向呈正弦分布的氣隙磁場。當時間改變，氣隙磁場將沿直線運動，稱之為行波磁場。行波磁場與永磁體產生的勵磁磁場交互作用，形成電磁推力，推動動子作直線運動，其方向與行波磁場運動的方向相反。因為是永磁體，故磁動勢可看做常量。

矢量控制基本思想是在三相交流電動機上設法模擬直流電動機轉矩控制的規律，為此，建立磁場定向坐標(d-q軸模型)，將電流矢量分解成產生磁通的勵磁電流分量id和產生轉矩的轉矩電流分量iq，并使兩分量互相垂直，彼此解耦，然后分別進行調節。由此得到d-q軸磁鏈方程及電壓方程為:

(1)

(2)

式中：ψd、ψq為d、q軸動子磁鏈， ψf為永磁磁鏈；ud、uq為d、q軸動子電壓，id、iq分別為d、q軸動子電流，ω為直線電動機對應的電角速度，Ld、Lq為d、q軸動子電感；R為動子電阻。

從上述方程可推得電磁推力方程：

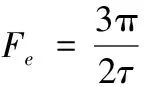
(3)

式中：Fe為電磁推力，τ為極距。可以看出，式(3)前一項是永磁直線電動機勵磁繞組的次級磁動勢和初級電樞反應磁動勢相互作用產生，后一項則由磁阻變化產生。

矢量控制的目標要求定子永磁體磁場與動子電流矢量在空間上正交，同時控制策略上令電流勵磁分量id=0，此時電磁推力Fe與iq將成正比，設直線電動機端部效應產生的等效阻力為Fd，則直線電動機的運動方程為：

(4)

式中：Kf為電磁推力系數； M為動子與負載總質量；B為粘滯摩擦系數；v為動子速度；F1為負載阻力；Fd為等效阻力。

進一步得到直線電動機的傳遞函數為：

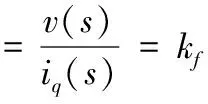
(5)

2 禁忌搜索算法的改進

禁忌搜索法是一種隨機搜索法，主要思想是先對每個解定義一個解的鄰域，從一個初始解出發，按照特定搜索方向(禁忌表)移動搜索，不斷迭代逐漸逼近最優解。為了提高搜索效率，本文對禁忌算法的鄰域范圍、Tabu 表和算法終止條件等做了改進，簡述如下。

2.1 鄰域范圍的動態調整

搜索初始階段，為了獲得盡可能多的周圍信息，鄰域范圍應設定的大一些，但這一鄰域若固定不變則影響后期搜索效率。本文在開始階段針對每個鄰域限定搜索次數，一旦超過則進入下一鄰域搜索，后期接近最優解時減小搜索范圍。

2.2 Tabu表的結構改造

一般Tabu 表存入某一步長L，凡是步長為L的移動全部被禁止， 這樣禁止的移動范圍有可能包含了一些對尋找最優解有益的移動，因此本文Tabu表不僅存入步長L，同時存入對應于這一步長的狀態點坐標，這樣做禁止的僅僅是圍繞某個狀態點周圍的鄰域范圍，禁止的范圍縮小了且更精確。

2.3 終止條件的改進

一般優化算法終止條件有兩種: ①預先設定一個最大迭代次數，但弊端是可能還未達到最優解就已經達到最大迭代次數。②預設一個最大誤差，但問題是優化前最優解并不知道。本文設計了一種動態終止條件：設定一個適當的迭代次數周期，將本次迭代周期內產生的最優值與上一次迭代周期的最優值相比較，如有改善則繼續，否則就終止。這一方法克服了單一判據的不足。

3 基于Tabu搜索的PID參數優化

本文的直線進給矢量控制系統應用在數控機床上，具有典型的三環結構，由外到內分別是位置環、速度環和電流環，按照工程經驗，位置環多采用P控制，速度環采用PID控制器，電流環采用PI控制，系統結構如圖1所示。

圖1 直線進給矢量控制系統框圖

直線進給矢量控制系統中需要優化的位置、速度和電流調節器PID參數(比例系數KP， 積分時間常數TI和微分時間常數TD)一共6個，首先需要對這些參數分別進行二進制編碼， 再組合成一個二進制碼串，構成Tabu搜索算法的初始解。

為了提高優化效率，需要對待優化的PID參數范圍進行初步估算，本文使用的估算方法不依賴數學模型，而是利用ZN工程整定法獲得基準PID參數，再向兩邊延拓。PID參數的搜索范圍由下列不等式確定：

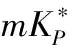
(6)

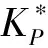
評價PID 控制器性能好壞的常用積分性能指標有誤差絕對值積分(IAE)、誤差平方積分(ISE)和時間乘以誤差平方積分(ITSE)。由于IAE和ISE沒有考慮時間因素，在得到相對較小超調的同時，需要較長的調節時間。ITSE 雖然考慮了時間因素，但其公式復雜并且費時。為此綜合直線進給系統的控制性能指標，提出如下簡單有效的適應度函數：

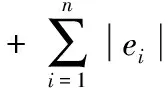
(7)

式中，權重系數w∈[0，1]，σ為超調量，ei為輸出誤差，tr為上升時間，ts為調節時間。搜索適應度函數f的最小值可保證獲得要求的最優性能指標，從而得到對應的一組最優控制參數KP、TI和TD。如果在迭代次數周期內適應度函數達到最小(不再改善)，算法終止。基于Tabu搜索的PID參數優化流程如圖2所示。具體步驟如下：

(1)初步設定算法參數，包括迭代周期、鄰域范圍、Tabu表長度等，Tabu表置空；

(2)在種群中任選某個個體作為當前解x，以當前解為起點，隨機產生若干鄰域解，將對應的PID參數用于直線進給系統，計算其適應度；

(3)判斷當前狀態點是否滿足禁忌要求，不滿足則跳轉到(5)；

(4)判斷當前狀態點是否滿足釋放條件,不滿足跳轉到(2)；

(5)對當前解x鄰域的若干個鄰域解對應的PID參數計算其適應度，取局部最優解；

(6)比較局部最優解與全局最優解來更新全局最優解；

(7)若沒有超過迭代周期或適應度有改善，則繼續下一次迭代，否則結束。

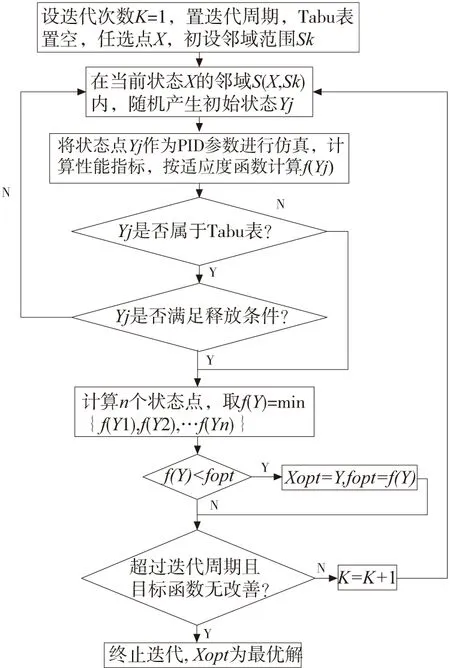
圖2 基于Tabu搜索的PID參數優化流程

4 系統實驗測試

為了驗證上述算法的優化效果， 本文以數控永磁直線進給矢量控制系統為對象，對基于傳統PID和基于Tabu優化PID的直線進給系統進行實驗對比研究。直線電機實驗平臺采用美國Kollmorgen公司的IC22-050A2P1系列組件，包括直線導軌(REXROTL)、動子(IC22-050A2P1)、磁鋼(MC050-0512)、驅動器(CB10560-000000)等。位置測量選擇了德國HEIDEHAIN公司的LIDA485光柵尺，精度等級為±5μm。組裝成型后的整機外形長度約為2000mm，凈行程約為1800mm。原系統有自己的控制器，為了驗證本文的優化控制策略，通過改變原有控制器中的參數設置，斷開驅動器內部的閉環回路，接入自己設計的以DSP為核心的控制器，并經RS-232C接口向驅動器下發控制指令，驅動器中實際參數反饋值由控制器上傳給上位計算機進行優化算法的分析與計算，得到相應的控制指令。直線進給實驗平臺如圖3所示，包括直線電機、伺服控制器、直線光柵、垂直與水平加載裝置等。上位機監控采用在線調試仿真軟件─MOTIONLINK。該軟件與伺服控制器之間通過RS-232C串口通信連接，并設計有相應的參數輸入、輸出結果數據及圖形顯示界面。

圖3 直線進給系統實驗平臺

直線電動機參數如下:動子質量M=6.9kg， 極距τ=32mm，粘滯摩擦系數B=0.2N·s/m，電磁推力系數kf=63N/A， 額定推力Fn=548N，額定電流In=8.7A。

應用Tabu算法對位置、速度和電流調節器的PID參數進行優化。適應度函數中w的取值是關鍵，主要根據系統對性能指標的要求來決定，若系統對動態響應速度要求高，則w值宜取小一點，如系統要求更小的超調和誤差，則w可以取大一點。本文的直線進給系統對跟蹤精度和超調量要求較高，因此加權系數w取為0.7，周期迭代次數設為100。適應度函數經過若干次迭代周期后如不再改善就得到最優PID參數，從而應用于直線進給系統。

在直線進給系統運行過程中，突然施加350N擾動力，得到傳統PID和Tabu優化PID控制系統的速度跟蹤曲線，將二者放在一起比較如圖4所示。圖5則是連續施加300sin(2πt) (N)正弦負載擾動后的速度跟蹤曲線。由圖可見，傳統PID控制不僅超調量大，負載干擾下轉速波動顯著，而經過Tabu 搜索算法優化后的PID控制系統，超調量小，轉速波動明顯改善，顯示其對抗外部干擾能力強，穩態精度和動態響應都高于傳統的PID控制器。圖6為輸入幅值為1.2 mm 的位置階躍信號指令，傳統PID和Tabu優化PID控制系統的位置跟蹤曲線，可明顯看出經Tabu優化PID的直線進給系統有更高的位置跟蹤精度。

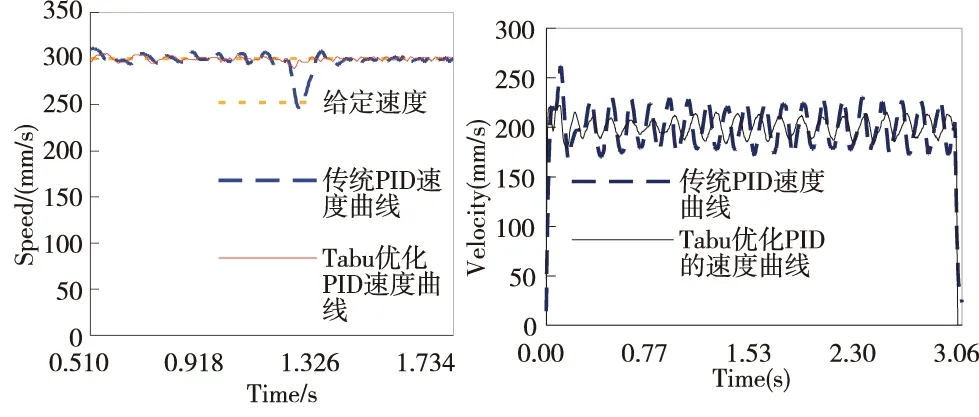
圖4 突加負載擾動后的速度跟蹤曲線圖5 連續正弦干擾下的速度跟蹤曲線

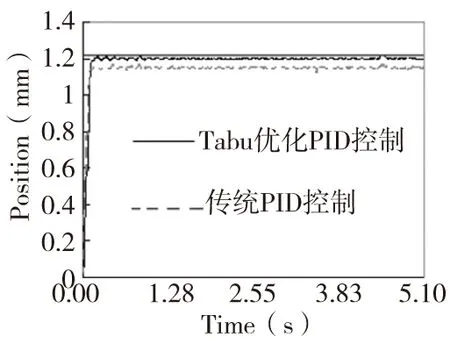
圖6 位置跟蹤曲線

5 結束語

直線進給矢量控制系統中各調節器PID參數的整定直接影響控制性能，工程上多采用實驗與經驗相結合的整定方法，本文采用Tabu搜索法對PID參數進行優化。為提高Tabu搜索的效率和精度，對鄰域搜索范圍、Tabu表規則、算法終止條件等算法要素進行了改進，并將Tabu搜索優化后的PID參數應用于直線進給矢量控制系統，實驗結果表明， 相比于傳統PID控制器，Tabu 優化的PID控制器，超調量、位置跟蹤精度等性能指標提高，轉速抗負載干擾的能力明顯增強。

[1] 劉春芳，杜昭童. 數控機床永磁同步直線伺服系統免疫控制[J]. 沈陽工業大學學報,2015,37(1):1-5.

[2] 王善華，楊龍，王保升．基于SVPWM的永磁直線同步電機直接推力控制[J]．組合機床與自動化加工技術，2015(6)：93-95．

[3] Youn S W， Lee J J， Yoon H S， et al. A new cogging-free permanent-magnet linear motor[J]. IEEE Transactions on Magnetics， 2008，44(7)： 1785-1790.

[4] 韓京清. 自抗擾控制技術—估計補償不確定因素的控制技術[M]. 北京: 國防工業出版社, 2008.

[5] 黃科元, 周滔滔, 黃守道, 等. 永磁伺服系統基于微分自適應補償的快速無超調控制策略[J]. 電工技術學報, 2014, 29(9): 137-144.

[6] 藍益鵬，邱超.磁懸浮永磁直線電動機懸浮系統模糊PID控制器的設計[J].機床與液壓，2013，41(7)：94-96.

[7] 韓明文，劉軍.永磁同步直線電動機徑向基神經網絡PID控制[J]. 微特電機，2012，40(6)：62-64.

[8] 盤真保，董菲,趙吉文,等. 基于遺傳二自由度的永磁同步直線電機PID控制參數優化研究[J]. 電氣工程學報,2015，10(8)：50-55.

[9] Dr’eo J，P’etrowski A，Taillard E．Metaheuristics for hard optimization [R]．Germany：Springer-Verlag，2006．

[10] 姚靜，方彥軍，陳廣．遺傳和禁忌搜索混合算法在機組負荷分配中的應用[J]．中國電機工程學報，2010，30(26)：95-100．

[11] 陳亮，傅闖，李興源．基于禁忌搜索算法的直流融冰計劃優化決策 [J]．電網技術，2015，39 (6)：1637-1642．

(編輯 李秀敏)

Vector Control of Linear Feed System Based on Tabu Algorithm Optimization

LIN Jian，LIU Kun，SHI Xin-xin，LIU Di

(School of Automation，Nanjing Institute of Technology，Nanjing 211167，China)

Linear feed vector control system of numerical control machine contains multiple PID controller whose control parameters directly affect system performance. Linear feed system is a complex nonlinear time-varying system，an improved Tabu optimization algorithm (Tabu) is presented and applied in the linear feed system to optimize PID regulator control parameters ,Based on the analysis of the existing Tabu search algorithm (Tabu), the neighboring regions, Tabu table and algorithms termination condition is improved. The linear feed system tracking performance indicators are taken as the objective function, all regulator PID parameters of linear feed vector control system are optimized based on the improved Tabu search algorithm, the experiment is carried out . The results show that , compared with conventional PID control, the optimized controller makes the motor speed fluctuation and position tracking error reduce significantly when the load changes,and steady-state and dynamic performance of the linear feed system are improved.

linear feed system；Tabu search；vector control；PID parameters optimization

1001-2265(2016)11-0080-04

10.13462/j.cnki.mmtamt.2016.11.022

2015-12-07；

2016-01-06

國家自然科學基金項目(61503180)；江蘇省自然科學基金項目(BK20130744)；江蘇省高校自然科學研究項目(13KJB120003)

林健(1971—)，男，南京人，南京工程學院教授，研究方向為數控機床的伺服控制，(E-mail)zdhxlj@njit.edu.cn。

TH166;TG659

A