基于自抗擾控制器的永磁同步電主軸速度擾動控制研究

孫榮俊，孫中圣，魯 明

(1.南京理工大學 機械工程學院，南京 210094； 2.北京控制工程研究所 機電中心，北京 100086)

?

基于自抗擾控制器的永磁同步電主軸速度擾動控制研究

孫榮俊，孫中圣，魯 明

(1.南京理工大學 機械工程學院，南京 210094； 2.北京控制工程研究所 機電中心，北京 100086)

針對傳統永磁同步電主軸(PMSS)調速系統在外部擾動或不確定參數變化等狀況下的速度控制性能不佳的問題，提出了速度環ADRC調節器的控制策略，該方法利用擴張狀態觀測器(ESO)對系統中的內外部“總擾動”進行估計及補償，并利用非線性狀態誤差反饋控制器(NLSEF)對跟蹤微分器(TD)的過渡過程與ESO產生的狀態估計的誤差進行非線性組合，實現優于經典PI調節器的線性組合的控制效果。仿真結果表明：在該控制策略下，PMSS具有良好的動態響應性能以及較強魯棒性。

永磁同步電主軸;速度環;自抗擾控制器

0 引言

電主軸將電機內裝于主軸本體內，具有結構緊湊、動態特性好的優點。它的應用實現了機床的“零傳動”，同時也改善了機床動平衡、減小了振動和噪聲[1]。隨著釹鐵硼等永磁材料成本的下降，加上永磁同步電主軸(permanent magnet synchronous spindle，PMSS)在性能和結構方面的優勢，PMSS勢必成為高端機床中的應用趨勢。

PMSS與永磁同步電機的驅動控制策略基本相同。PMSS調速系統可以近似為一階積分型線性系統[2]，在其通常使用的矢量控制器中，速度環調節器大都采用PI調節器，而經典PI調節器存在以下劣勢[3]：對增益的變化很敏感，存在“快速性”和“超調”的矛盾，積分反饋易造成振蕩和積分飽和。

PMSS是一個非線性、強耦合、參數時變的系統，當系統模型參數存在攝動或存在外部擾動，經典PI調節器的控制性能就顯得不盡人意了。為此不少學者就具有高動、靜態性能和魯棒性的速度環調節器做了不少研究。劉穎等人在滑模變結構控制的基礎上引入積分補償和擾動觀測器環節[4]，魯文其等人提出了抗擾動自適應控制[5]，這兩種控制策略都具有較好的動靜態性能和魯棒性，但都依賴于精確的系統模型。毋華麗提出了一種基于哈密頓系統理論的雙環路魯棒控制方法，提高系統對負載擾動的魯棒性[6]，但系統設計過于繁瑣。Nga Thi-Thuy Vu等人提出了一種基于確定性等價原理的魯棒自適應速度控制器，該控制器不需精確知道系統模型參數且能快速適應系統參數和負載轉矩變化[7]。Z·Hashemi等人提出了一種抗積分飽和的PI調制器，并利用遺傳算法對該控制器的參數進行訓練及優化[8]，但該方法計算量大，實時性較差。

本文針對PMSS運行過程中由于負載轉矩、摩擦系數以及轉動慣量等參數攝動和外部不確定擾動造成的系統性能下降的問題，設計了速度環自抗擾控制器(Active-Disturbance Rejection Controller，ADRC)，其能夠有效地對系統內外擾動進行估計并加以補償，且不依賴于系統模型[9]。

1 PMSS數學模型

為簡化PMSS的數學模型，首先作如下假設：

(1)忽略鐵心飽和及磁滯損耗；

(2)不考慮轉子的阻尼效應；

(3)相繞組中感應電動勢波形為正弦波；

(4)電機參數不受影響。

則PMSS在d-q軸下的電壓方程和轉矩方程可分別表示為式(1)和式(2)：

(1)

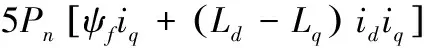
(2)

忽略系統的靜摩擦和庫倫摩擦，只考慮黏性摩擦，易知PMSS的運動方程可表示為式(3)：

Te=Jpwr+Tl+Rwr

(3)

式中:ud,uq，id,iq，Ld,Lq分別為d-q軸下的定子電壓，電流，電感；we,wr分別為轉子的電角速度和實際角速度；Ψf為永磁體磁鏈；RS為定子電阻；p為微分算子；Te為電磁轉矩；Pn為極對數；J為轉子和所帶負載的總轉動慣量；Tl為負載轉矩；R為粘滯摩擦系數。

2 自抗擾控制器

自抗擾控制器(ADRC)是一種非線性控制器，其標準結構包含三個子模塊：跟蹤微分器(Tracking Differentiator, TD)，擴張狀態觀測器(Extended State Observer, ESO)[10]，非線性狀態誤差反饋控制器(Nonlinear State Error Feedback, NLSEF)[11]。圖1是一個常用二階ADRC的結構示意圖。

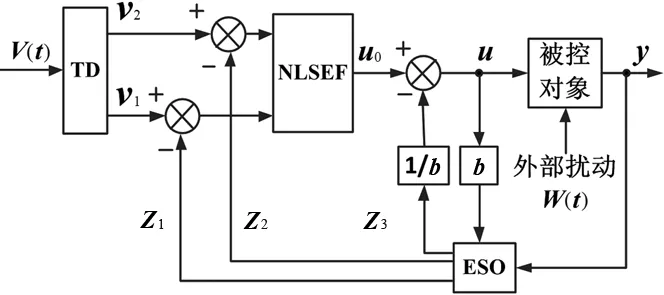
圖1 二階ADRC結構框架

2.1 跟蹤微分器(TD)

如圖1所示，TD將輸入信號v(t)處理后，輸出對應的跟蹤信號v1和一階微分信號v2。這樣，當輸入信號為突變信號時，經過TD的處理可提供光滑而連續的輸出信號作為輸入，并送進控制器，使得系統不會因為受到突變的輸入信號而出現超調。TD對輸入信號安排了合適的過渡過程，減小了初始誤差，解決了超調與快速性的矛盾。常用二階非線性跟蹤微分器的一般形式如式(4)所示:

(4)

其中：

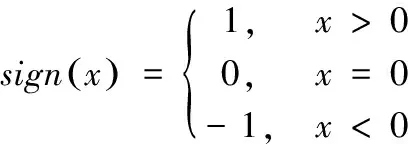
(5)

2.2 擴張狀態觀測器(ESO)

ESO是ADRC的核心，其品質很大程度上決定了ADRC的性能。如圖1所示，ESO只用到原對象的輸入和輸出(即u和y)，是獨立于描述對象傳遞關系的具體形式[3]，所以其不依賴系統模型。ESO可跟蹤被控對象的各階次狀態變量z1、z2、z3，對來自系統內部和外部未知的各種擾動作用進行估計及補償。常用三階非線性擴張狀態觀測器如式(6)所示:

(6)

其中：

(7)

2.3 非線性狀態誤差反饋控制器(NLSEF)

NLSEF是一種廣義非線性的PID控制器，其常用二階非線性狀態誤差反饋控制率如式(8)所示。如圖1所示，NLSEF將TD的過渡過程(v1、v2)與ESO產生的狀態估計(z1、z2)的誤差(ε1、ε2)進行非線性組合，結合ESO的擾動估計量的補償來產生實際控制信號u，具有小誤差大增益，大誤差小增益的優點[12]。

(8)

ESO中的狀態變量Z3用來跟蹤擾動總和a(t)，利用其進行擾動補償，可得到實際的控制量u。

u=u0-z3/b

(9)

3 ADRC在PMSS中的應用

3.1 基于ADRC的速度環設計

由PMSS的運動方程(式(3))推導可得到轉速的一階微分方程：

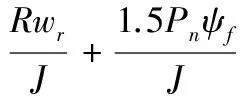
(10)

設計速度環時，將系統的轉速wr作為目標輸出y，d-q軸下的電流iq作為控制量輸入u，狀態變量x用于跟蹤轉速wr，令a(t)=1.5Pn(Ld-Lq)idiq/J-Tl/J-Rwr/J，b=1.5PnΨf/J，則PMSS速度環的狀態方程可表示為：

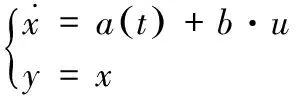
(11)

由自抗擾控制技術理論可知，PMSS轉速的總擾動a(t)來自于內部模型擾動1.5Pn(Ld-Lq)idiq/J及外部擾動-Tl/J-Rwr/J。由于本文的研究對象為隱極式PMSS(Ld=Lq)，所以不存在內部模型擾動，即式(10)可簡化為式(12):

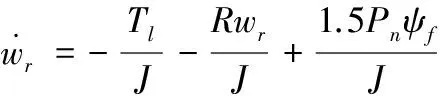
(12)

此外，參數b理論上由電機參數計算得到，但與電機實際模型參數存在誤差，用b0對模型參數b進行近似估計，將b0與b的誤差作為一種擾動，利用ESO對其進行估計及補償。因此總擾動為a(t)=-Tl/J-Rwr/J+(b-b0)u，反映了由負載轉矩、摩擦系數以及轉動慣量等參數攝動和不確定擾動[3]，其中負載突變影響最大。由此，可以構建基于ADRC的速度環調節器，其結構框架圖如圖2所示。

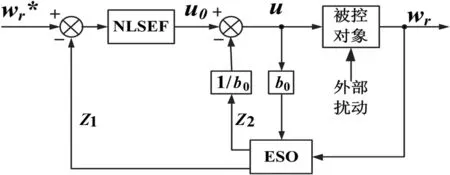
圖2 一階速度環ADRC結構框架

由于本系統為一階的，因此在設計ADRC調節器時，取消了TD模塊，直接將參考速度送給ADRC調節器。具體ADRC各模塊表示如式(13)、式(14)所示:

ESO：

(13)

NLSEF：

(14)

3.2 ADRC的參數整定

ADRC的參數整定采用分離性原理[3-12]。

(1) ESO中的參數：β01，β02，α01，δ01，b0

其中β01，β02是ESO中的反饋增益，類似于PID參數中的P參數，其取值越大響應速度越快，但過大會產生超調和震蕩，因此其整定時首先要保證ESO的穩定。α01和δ01是fal(e,α,δ)函數的參數，α01為非線性參數(α01=1時，為線性函數)，初始值一般取0.5，然后再進行微調，δ決定fal(e,α,δ)函數的線性區域的寬度，過大會使得控制器只能工作在線性區域，起不到非線性反饋控制的目的，過小會出現顫振的問題。b0是模型參數b的近似估計值，作為可調參數進行調整，b0越大響應速度越快，但過大會導致超調及震蕩。

(2) NLSEF中的參數：β11，α11，δ02，b0

NLSEF中的參數整定方法與ESO中的參數整定策略對應相一致，b0同上。

4 仿真與分析

根據ADRC控制器原理，結合PMSS數學模型設計了PMSS一階ADRC速度環調節器，利用S函數構建了ADRC以及利用Simulink框圖模塊建立了PMSS驅動系統仿真模型，具體仿真模型如圖3所示。仿真參數如下：PMSS的額定速度n=2200rpm，Pn=4，RS=0.13Ω，L=0.0015H，Ψf=0.1821Wb，J=0.00333kg.m2。直流母線電壓Udc=300V，逆變側調制周期TS=0.0002s。ADRC的參數分別為：ESO中的α01=0.11、δ01=0.01、β01=7、β02=5000，NLSEF中的α11=0.505、δ02=0.01、β11=0.008，b0=164。

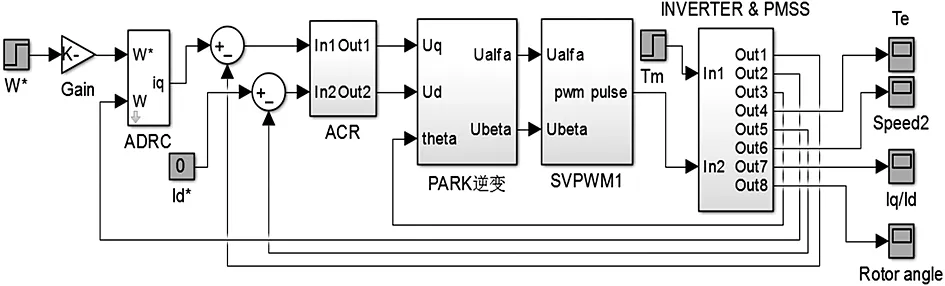
圖3 基于ADRC控制器的PMSS仿真模型

仿真內容包含：①轉速由0～1000rpm的階躍響應仿真；② 0.02s時刻突加負載(10N·m)的速度響應仿真。

0到1000rpm的階躍響應的仿真結果如圖4、圖5所示，可以看出經典PI調節器下的階躍響應出現了超調(4.2rpm)，調節時間(速度上升到穩態值的±2%誤差范圍所需要的最小時間)為0.0121ms，穩態誤差為0.6rpm；而使用ADRC時，系統無超調，調節時間為0.011ms，穩態誤差為0.3rpm。對比而言，ADRC具有更優的動靜態特性。

突加負載(10N·m)的轉速響應的仿真結果如圖6所示，圖7、圖8分別為突加負載的轉速響應曲線的局部放大圖，可以看出使用經典PI調節器時，突加負載的瞬間，速度有一個6.4rpm的下降，且速度恢復時間很長，這是由于原來的PI參數是針對突加負載前的工況進行整定的，突加負載后已不適應，這也說明了其閉環動態品質對PI增益的變化很敏感。使用ADRC時，起初有一個3.5rpm的速度跌落，但之后迅速恢復到設定值。對比而言，在外部擾動的情況下，采用ADRC的系統有更小的速度變化和恢復時間，可更好地抑制因負載突變所帶來的影響，因此ADRC具有更強的魯棒性。

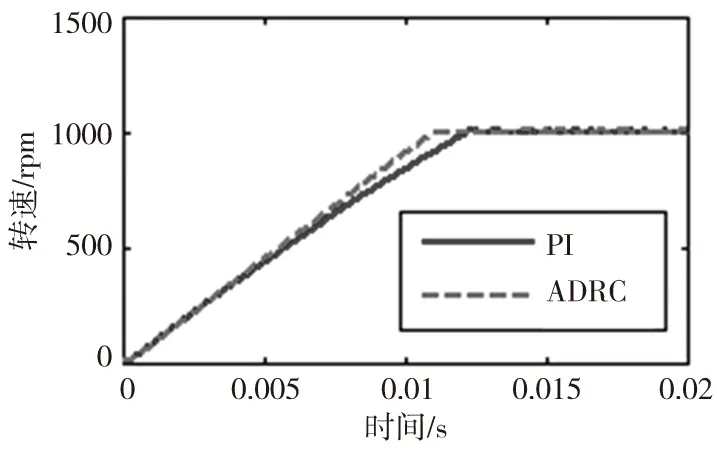
圖4 階躍響應(0～1000rpm)

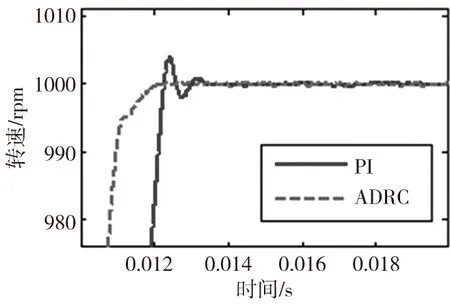
圖5 階躍響應局部放大圖

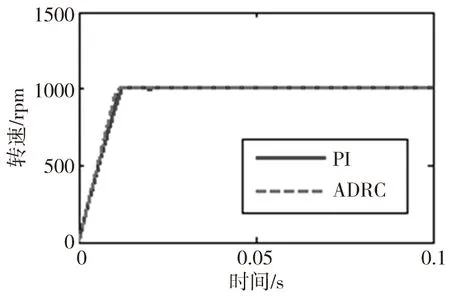
圖6 突加負載的轉速響應(10N·m)

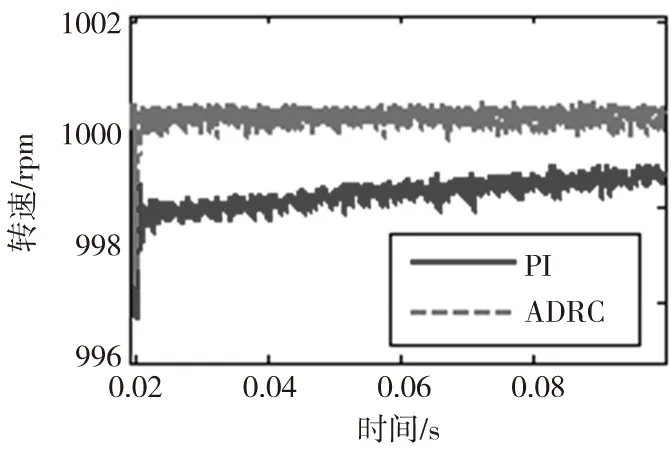
圖7 突加負載的轉速響應圖的局部放大圖I

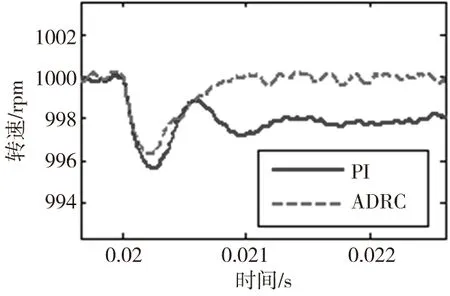
圖8 突加負載的轉速響應圖的局部放大圖II

5 結論

本文在分析速度環PI調節器不足的基礎上，利用自抗擾控制技術設計了速度環ADRC調節器，建立了一階速度環ADRC模型，并對其進行了仿真與分析。仿真結果表明，本文提出的速度環ADRC調節器相較于經典PI調節器具有更好的動靜態特性及更強的魯棒性。此外，ADRC的待整定參數相對較多，雖可以利用獨立性原則按照一定的規律進行參數整定，但需要相對較深的理論基礎和經驗，所以ADRC的參數整定是一個難點。但還是有一些ADRC參數整定的優化方法的，如基于CPSO的ADRC參數整定法[13]，基于遺傳基因算法的ADRC參數整定法[14]，基于粒子群優化算法的ADRC參數優化[15]等。總之，利用整定好參數的ADRC調節器可以獲得比經典PI調節器更佳的性能。

[1] 楊貴杰,秦冬冬. 高速電主軸的關鍵技術及發展趨勢[J].伺服控制,2010(2):34-36.

[2] 劉志剛,李世華. 永磁同步電機的二階自抗擾控制算法

[A].第二十六屆中國控制會議論文集[C].中國自動化學會控制理論專業委員會,2007:68-71.

[3] 韓京清. 自抗擾控制技術：估計補償不確定因素的控制技術[M]. 北京：國防工業出版社,2013.

[4] 劉穎,周波,方斯琛. 基于新型擾動觀測器的永磁同步電機滑模控制[J].中國電機工程學報, 2010,30(9):80-85.

[5] 魯文其, 胡育文, 梁驕雁, 等. 永磁同步電機伺服系統抗擾動自適應控制[J].中國電機工程學報,2011,31(7):75-81.

[6] 毋華麗. 基于哈密頓系統理論的永磁同步電動機魯棒控制[D].鄭州:鄭州大學,2013.

[7] Nga Thi-Thuy Vu, Han Ho Choi,Jin-Woo Jung. Certainty equivalence adaptive speed controller for permanent magnet synchronous motor[J]. Mechatronics,2012, 22(6):811-818.

[8] Hashemi Z, Mardaneh M, Sha Sadeghi M. High performance controller for interior permanent magnet synchronous motor drive using artificial intelligence methods[J]. Scientia Iranica,2012,19(6):1788-1793.

[9] 劉麗英,許鎮琳,梅強. 基于線性自抗擾控制器的異步電機調速系統[J]. 組合機床與自動化加工技術,2009(5):56-60.

[10] 韓京清. 一類不確定對象的擴張狀態觀測器[J]. 控制與決策,1995,10(1):85-88.

[11] 韓京清. 非線性狀態誤差反饋控制律—NLSEF[J]. 控制與決策,1995,10(3):221-225.

[12] 劉清. 基于自抗擾控制器的永磁同步電機伺服系統控制策略的研究及實現[D].天津:天津大學,2011.

[13] Liu Chunfang, Zang Bin. Application and the parameter tuning of ADRC based On CPSO[C]. Chinese Control and Decision Conference, 2012:3277-3281.

[14] Zeng Wenfei, Yan Ling. The parameter setting and application study of ADRC based on immune genetic algorithm[C]. in 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems, 2010:183-186.

[15] Ping Wang, Hua Wang, Guoyu Bai, et al. Parameter Optimization of ADRC for Spacecraft Attitude Maneuver Based on Particle Swarm Optimization Algorithm[C]. in Sixth International Conference on IHMSC, 2014:194-197.

(編輯 李秀敏)

Study of PMSS Speed Disturbance Control Based on ADRC

SUN Rong-jun1，SUN Zhong-sheng1，LU Ming2

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2.Mechanical and Electrical Center, Beijing Institute of Control Engineering, Beijing 100086, China)

The control performance of traditional drive system of the permanent magnet synchronous spindle(PMSS) is poor when there is an external disturbance or an uncertain parameters changing, so the control strategy of speed-loop ADRC regulator is proposed. In this method, the total disturbance of the system is estimated and compensated by using ESO; and nonlinear combination of the errors is done by NLSEF. The simulation results show that the PMSS has good dynamic performance and strong robustness by this control strategy.

PMSS; speed-loop; ADRC

1001-2265(2016)11-0108-04

10.13462/j.cnki.mmtamt.2016.11.029

2016-01-15

國防科工局軍用技術推廣科研項目(科工技[2014]750)

孫榮俊(1990—)，男，江蘇興化人，南京理工大學碩士研究生，研究方向為永磁同步電機驅動技術，(E-mail)rongjun.sun@foxmail.com。

TH164;TG506

A