五等跨連續(xù)梁模態(tài)分析試驗及沖擊系數(shù)

劉 輝， 袁向榮， 蔡卡宏， 胡幫義， 張 盼

(廣州大學 土木工程學院，廣東 廣州 510006)

?

五等跨連續(xù)梁模態(tài)分析試驗及沖擊系數(shù)

劉 輝， 袁向榮， 蔡卡宏， 胡幫義， 張 盼

(廣州大學 土木工程學院，廣東 廣州 510006)

分析計算五等跨連續(xù)梁的固有頻率和振型，探討連續(xù)梁橋沖擊系數(shù)與其固有頻率和振型的關系，并進行了連續(xù)梁振動試驗，試驗模型采用槽型梁，支撐方式采用鋼錕軸支撐，試驗結果運用DASP模態(tài)分析軟件進行處理，得到五等跨連續(xù)梁的前5階振型及頻率。利用Midas有限元分析軟件對連續(xù)梁進行有限元分析，將其計算結果與試驗結果進行對比，證實振型變化的真實性。經(jīng)過試驗分析，連續(xù)梁的前5階振型最大曲率位置被確定，結合規(guī)范討論計算沖擊系數(shù)時結構固有頻率的選取。結果表明：當計算跨中正彎矩效應時，沖擊系數(shù)宜按照《橋規(guī)》采用基頻計算；當計算中支座負彎矩效應時，沖擊系數(shù)應采用第3階頻率。

五等跨連續(xù)梁； 振型； 沖擊系數(shù)； 有限元分析； 模態(tài)分析

0 引 言

連續(xù)梁橋是中等跨徑橋梁中常用的一種橋梁結構形式，在現(xiàn)代化橋梁設計中，連續(xù)梁橋得到了廣泛的應用，為了可以較準確的反映橋梁結構在動載作用下的動力增大效應，我們通過沖擊系數(shù)加以體現(xiàn)。為確保橋梁安全運營，在橋梁結構設計或分析計算時，汽車荷載的總效應應由汽車靜載效應乘以沖擊系數(shù)加以量化考慮[1]。

閆永倫等[2]針對《公路橋涵設計通用規(guī)范》(JTJ021-89)中“沖擊系數(shù)”的規(guī)定，提出了制定我國公路橋梁荷載放大譜的建議?！豆窐蚝O計通用規(guī)范》[3](JTG D60-2004)(以下簡稱《橋規(guī)》)采納了該建議，采用橋梁基頻的函數(shù)來計算沖擊系數(shù)。

《橋規(guī)》4.3.2第4款規(guī)定，汽車荷載的沖擊力標準值為汽車荷載標準值乘以沖擊系數(shù)μ，第5條規(guī)定：當f<1.5 Hz時，μ=0.05；1.5 Hz≤f≤14 Hz時，μ=0.176 7 lnf-0.015 7；f>14 Hz時，μ=0.45，其中，f為結構基頻(Hz)。

沖擊系數(shù)反映了汽車動荷載對橋梁的沖擊作用[4]，《橋規(guī)》中針對連續(xù)梁沖擊系數(shù)的取值由其固有頻率所決定。目前關于沖擊系數(shù)計算的研究主要包括：①根據(jù)車輛耦合振動計算探討沖擊系數(shù)[5-7]；②根據(jù)橋梁動載試驗實測數(shù)據(jù)研究沖擊系數(shù)[8-10]；③將我國現(xiàn)行規(guī)范與國外規(guī)范對照比較，或對我國新舊規(guī)范進行比較[2,7,11-12]。

模態(tài)分析對于振動工程來說至關重要[13-14]，通過分析可以識別結構體系的模態(tài)參數(shù)，目前連續(xù)梁振動的模態(tài)分析理論研究較成熟[15-16]。模型與實際試驗的頻率識別較多，但振型識別較少，而模態(tài)疊加法的基礎在于振型，振型對于橋梁沖擊系數(shù)有較大影響[17]。模型試驗研究對于多跨連續(xù)梁模態(tài)分析至關重要，吳晶等[18-20]對二、三、四跨連續(xù)梁進行了模態(tài)分析計算和試驗研究，胡幫義等對二等跨曲線連續(xù)梁橋進行了研究，得到了曲梁的前4階頻率及振型；羅川舟等對不同跨徑組合的三跨連續(xù)梁的振型及頻率進行了對比分析；而五跨連續(xù)梁還沒有試驗研究。

總之，《橋規(guī)》針對沖擊系數(shù)的規(guī)定是適應的，但連續(xù)梁模態(tài)分析試驗除產(chǎn)生1階頻率外，高階頻率也隨之產(chǎn)生，所以研究高階頻率對橋梁結構沖擊系數(shù)的作用是不可缺少的。姜長宇等的研究表明，對于連續(xù)梁橋，沖擊系數(shù)的計算僅使用基頻是不合理的，因此，完整的模態(tài)分析對于連續(xù)梁橋必不可少。袁向榮[17]基于連續(xù)梁振動分析，指出奇數(shù)跨連續(xù)梁第3階振型在中支點處曲率較大，故沖擊系數(shù)應采用第3階頻率計算。

橋梁結構設計的合理性取決于沖擊系數(shù)的合理取值。本文對五等跨連續(xù)梁進行了模態(tài)分析試驗，得到其前5階頻率及振型，結合試驗結果及有限元分析結果，進一步探討了沖擊系數(shù)的計算，為今后連續(xù)梁沖擊系數(shù)的計算提供一定的參考。

1 五等跨連續(xù)梁試驗模型

試驗對象為五等跨等截面連續(xù)梁模型，梁長5.5 m，橋跨布置為5×1.1 m，共設6個支座，編號為1～6。支承方式為鋼輥軸，支座1采用砝碼壓重約束構成固定支座，其他支座采用直徑2.5 cm鋼管形成活動支座。連續(xù)梁材料采用槽型，橫截面如圖1所示。

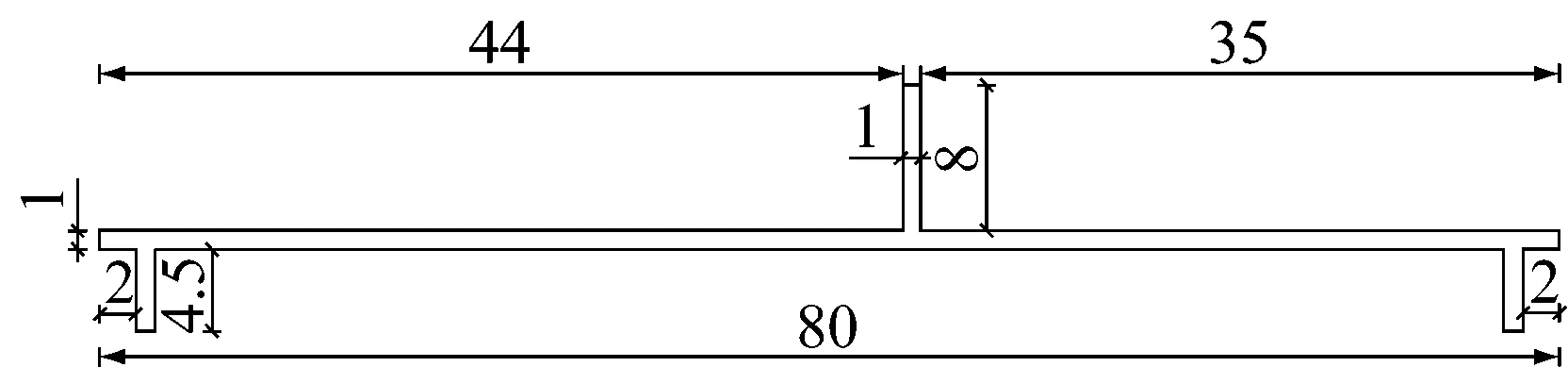
圖1 連續(xù)梁橫截面圖(mm)

材料參數(shù)取值：彈性模量E=70 GPa，泊松比υ=0.3，線膨脹系數(shù)為1.2×10-5/℃，容重Dens=28 kN/m3。試驗模型如圖2所示。

圖2 連續(xù)梁試驗模型

2 連續(xù)梁有限元模態(tài)分析

2.1 有限元模型建立

通過Midas Civil 有限元軟件建立連續(xù)梁有限元計算模型，為使計算結果更加精確，對空間梁單元進行單元劃分，將其劃分為30個梁單元，并進行各種參數(shù)調整。然后進行邊界條件處理，對于固定支座1約束其x、y、z方向的位移，其他支座為可動鉸支座，只約束z方向位移，模型計算采用集中質量法，將質量轉化到z方向。由于加速度傳感器的存在，所以在有限元建模時應將每個傳感器位置施加一集中力，即G=mg=0.143×9.8=1.40 N，運用將荷載轉化為質量的方法施加在模型上，特征值分析設置為子空間迭代，建立的五等跨有限元分模型如圖3所示。

圖3 有限元分析模型

2.2 有限元計算結果

通過有限元計算分析，得到連續(xù)梁前5階固有頻率及振型，頻率如表1所示，振型如圖4所示。

表1 連續(xù)梁各階頻率理論值

(a) 1階

(b) 2階

(c) 3階

(d) 4階

(e) 5階

圖4 連續(xù)梁各階理論振型圖

3 連續(xù)梁模態(tài)分析試驗

3.1 實驗儀器及設備連接

本實驗所用試驗設備有：INV3060V2智能信號采集處理分析儀1臺，BI1148型壓電加速度傳感器10個，聯(lián)想Y470筆記本電腦1臺，DASP V10智能分析軟件1套，數(shù)據(jù)線若干。試驗設備連接方式如圖5所示。

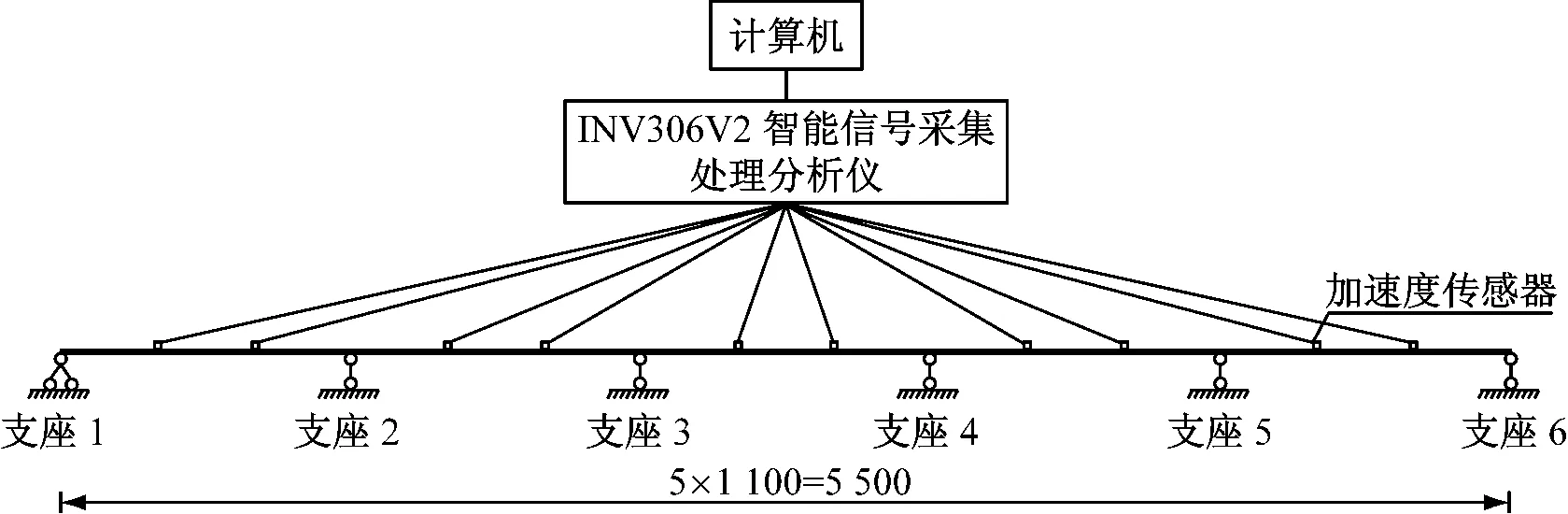
圖5 試驗設備連接示意圖

3.2 試驗方法

由于本次試驗結構為小型模型試驗，所以對試驗對象的激勵采用錘擊法[18]。

3.3 實驗過程

首先根據(jù)試驗要求布置好橋跨和傳感器位置，確保各線路暢通及各傳感器通道信號顯示正常；其次對各通道進行數(shù)據(jù)標定及各種參數(shù)的調整；然后對試驗對象進行錘擊，采用一點錘擊多點測量的辦法對實驗對象進行激勵，同時用信號采集儀采集振動信號并傳入筆記本電腦，最后把傳入電腦的信號用DASP模態(tài)分析程序自動導出傳遞函數(shù)和頻響函數(shù)，對頻響函數(shù)進行集總平均，選擇恰當?shù)念l率定階。最終進行實模態(tài)多自由度擬合，便得到結構的自振頻率及其振型圖[18]。

3.4 試驗結果

通過DASP模態(tài)分析軟件分析各測點的頻響函數(shù)曲線得到連續(xù)梁的前5階模態(tài)頻率及振型幅值。各階頻率如表2所示，振型幅值如表3所示，各階振型圖如圖6所示。

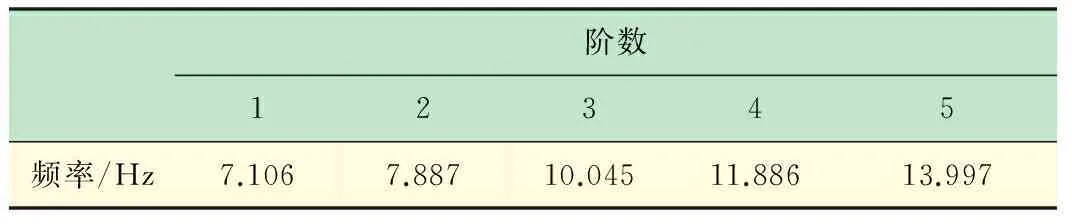
表2 各階頻率試驗值

表3 各階實測振型幅值

(a)1階

(b)2階

(c)3階

(d)4階

(e)5階

圖6 五等跨連續(xù)梁前5階實測振型圖

4 結果及對比分析

連續(xù)梁試驗結果與有限元所得結果列于表4。結果表明：連續(xù)連第3階頻率相對誤差僅0.2%，第1、2階相對誤差相等為2.1%，第4、5階相對誤差相對較大，但都小于8%；由圖4和圖6振型圖可知，試驗測得振型與有限元計算所得振型基本相同；試驗所得連續(xù)梁前5階固有頻率均小于有限元計算頻率。

《橋規(guī)》中結構固有頻率為沖擊系數(shù)計算公式的唯一變量，因此，有必要分析固有頻率所對應的振型和動彎矩的關系[17]。

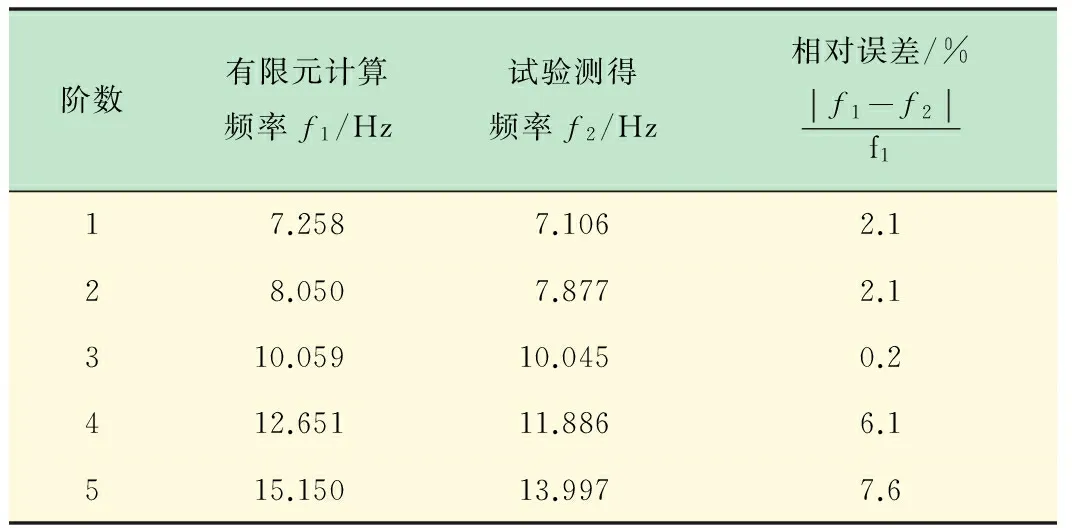
表4 有限元結果與試驗結果對比

由力學知識可知：梁彎曲時，距中性層距離y的纖維應變?yōu)椋?/p>

(1)

根據(jù)幾何關系有：

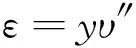
(2)

式中：υ″為中性軸的曲率。聯(lián)立式(1)、(2)有：

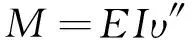
(3)

由式(3)可知，動彎矩M與曲率υ″成正比，即梁的動彎矩隨著曲率的增大而增大。按照振動理論[16]，振型組成梁振動的完備空間，梁在荷載作用下的動彎矩是其振型的線性組合。對五等跨連續(xù)梁1階振型，各跨最大曲率均在跨中，而其在線性組合中所占比重最大，故最大動彎矩也在跨中。因此計算跨中正彎矩效應時，沖擊系數(shù)采用基頻是合理的。

當考慮支點負彎矩效應時，由圖4可知，中支點的曲率最大值在第3、4、5階振型中均有出現(xiàn)，雖然第4、5階在中間支座處曲率稍大，但是第3階振型先出現(xiàn)曲率最大值，故計算中支點負彎矩效應時，沖擊系數(shù)應采用第3階頻率。

5 結 論

通過有限元計算和試驗測試的對比分析，可以得到以下結論：

(1)試驗測試分析與有限元分析所得結果除第4、5階頻率相對誤差較大外，其他各階相對誤差均小于4%，其頻率最大為7.6%，最小為0.1%，試驗測得振型與有限元計算振型基本吻合。因此利用模態(tài)分析理論對連續(xù)梁進行動力特性研究基本是可行的，同時對這兩種方法的計算結果進行了相互驗證。

(2)對五等跨連續(xù)梁橋，其第1階模態(tài)對各跨跨中動彎矩起主要作用，此時跨中處沖擊系數(shù)最大，因此當計算跨中正彎矩效應時，依據(jù)《規(guī)范》采用基頻計算沖擊系數(shù)是合理的。考慮支座負彎矩效應時，則不能只按基頻計算其沖擊系數(shù)，應按第3階頻率計算。

(3)對于連續(xù)梁橋沖擊系數(shù)的計算只考慮第1階頻率是不合理的，故在計算連續(xù)梁沖擊系數(shù)時，應根據(jù)結構通過有限元計算的頻率和振型，參考結構振型最大曲率與正負彎矩選擇頻率，并用此頻率按照相關規(guī)范計算沖擊系數(shù)。

通過試驗分析，可以計算連續(xù)梁的各階模態(tài)參數(shù)，為今后實際橋梁的健康監(jiān)測提供了參考，也為結構尺寸不詳?shù)默F(xiàn)有橋梁的結構優(yōu)化設計和有限元建模提供動力學模態(tài)參數(shù)參考。

[1] 許 鵬. 橋梁結構沖擊系數(shù)影響因素研究與試驗分析[D]．重慶：重慶交通大學，2013：5-13．

[2] 閆永倫，周建廷. 關于我國現(xiàn)行《公路橋涵設計通用規(guī)范》“沖擊系數(shù)”規(guī)定的幾點探討[J]．公路,2003(6):14-16．

[3] JTG D60-2004.公路橋涵設計通用規(guī)范[S]．2014.

[4] 王海城，施尚偉. 橋梁沖擊系數(shù)的影響因素及偏差成因[J]．重慶交通大學學報(自然科學版),2007,26(5): 25-28．

[5] 盛國剛，彭 獻，李傳習. 連續(xù)梁橋與車輛耦合振動系統(tǒng)沖擊系數(shù)的研究[J]．橋梁建設，2003(6): 5-7．

[6] 張元文，姜長宇. 公路連續(xù)梁橋沖擊系數(shù)的探討[J]．山西建筑,2008,34(14): 347-348．

[7] 桂水榮，陳水生，任永明. 先簡支后連續(xù)梁橋車輛沖擊系數(shù)影響因素研究[J]．公路交通科技,2011,28(5): 54-60．

[8] 施尚偉，趙 劍，舒紹云. 梁橋沖擊系數(shù)實測值與規(guī)范取值差異分析[J]．世界橋梁,2010(2): 80-82．

[9] 許士強，陳水生，桂水榮. 公路橋梁汽車沖擊系數(shù)對比研究[J]．工程建設與設計,2006(12): 73-75．

[10] 孫偉良. 多跨先簡支后連續(xù)鋼筋混凝土空心板橋梁沖擊系數(shù)研究[J]．石家莊鐵道學院學報,2007,20(2): 52-56．

[11] 漆景星. 公路橋梁沖擊系數(shù)計算方法研究[J]．公路，2011(7):85-88．

[12] 劉 舒，王宗林. 關于新舊規(guī)范中沖擊系數(shù)的討論[J]．中國科技信息,2005(23): 121．

[13] 梁 君，趙登峰. 模態(tài)分析方法綜述[J]．現(xiàn)代制造工程,2006(8):139-141.

[14] 龍 英，滕召金，趙福水. 有限元模態(tài)分析現(xiàn)狀與發(fā)展趨勢[J]．湖南農(nóng)機,2009,36(4):27-28,45.

[15] 宋一凡．公路橋梁動力學[M]．北京：人民交通出版社，2000．

[16] 劉晶波，杜修力．結構動力學[M]．北京：機械工業(yè)出版，2005．

[17] 袁向榮. 基于連續(xù)梁振動分析的橋梁沖擊系數(shù)研究[J]．四川建筑科學研究, 2013,39(4):190-194.

[18] 吳 晶，袁向榮. 兩等跨連續(xù)梁的模態(tài)分析試驗[J]．長春工程學院學報(自然科學版),2012,13(1):1-2,26.

[19] 鄭仰坤，袁向榮. 不同跨徑比的兩跨連續(xù)梁的模態(tài)分析試驗[J].噪聲與振動控制, 2014,34(4):148-152.

[20] 胡幫義，袁向榮，陳澤賢，等. 四等跨連續(xù)梁模態(tài)試驗分析及沖擊系數(shù)研究[J].實驗技術與管理, 2015,32(8):70-74.

Modal Analysis Test to a Five Equal Spans Continuous Beam and Study of Impact Factor

LIUHui,YUANXiang-rong,CAIKa-hong,HUBang-yi,ZHANGPan

(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

The natural frequency and vibration mode of 5 equal spans continuous beam was analyzed, the relation between the impact factor of continuous beam and the natural frequencies and vibration mode was discussed, and these dynamic parameters of continuous beam modal were measured. Test model used groove type beam, supporting way was with steel shaft support, the DASP equipment was used for modal analysis to obtain the first five vibration modes and frequencies of 5 equal spans continuous beam. The finite element analysis software Midas was used for continuous beam. The simulation results were compared the measured data, the authenticity of the vibration mode change was verified. From the test analysis, the locations of the maximum curvatures of the mode shapes were determined, the selection of the natural frequency of the beam was discussed with the design code. It is shown that, when calculating the effect of positive bending moment at steady, the fundamental frequency should be used as shown in the general code to calculate the impact factor; when calculating the effect of negative bending moment at middle fulcrum, the 3rd frequency should be used.

five spans continuous beam; vibration mode; impact factor; finite element analysis; modal analysis

2015-07-22

國家自然科學基金(51078093,51278137)；廣州市科技計劃項目(12C42011564)

劉 輝(1991-)，男，河南泌陽人，碩士生，研究方向為橋梁工程、數(shù)字圖像處理。

Tel.:18826223674；E-mail: 18826223674@163.com

U 441.3

A

1006-7167(2016)05-0010-04