基于模糊PID控制的ABS系統研究

張利，宋年秀，于明曉

（青島理工大學汽車與交通學院，山東青島 266520）

基于模糊PID控制的ABS系統研究

張利，宋年秀，于明曉

（青島理工大學汽車與交通學院，山東青島 266520）

在MATLAB／Simulink中建立汽車制動防抱死系統（ABS）仿真模型，以單輪車輛模型為研究對象，以模糊PID控制器為控制模塊，對ABS模型進行仿真研究。結果表明基于模糊PID控制器的ABS系統能根據變化時刻對相關參數進行調節，能適應不同路面，且都能達到良好的制動效果。

汽車；制動防抱死系統（ABS）；模糊PID控制器；制動效果

制動系統是車輛安全系統的重要組成部分之一，制動性能也是保證車輛安全行駛的必要性能。大多數交通事故是由于汽車緊急制動時車輪抱死引起的，制動防抱死系統（ABS）可防止車輪抱死，從而減少這類事故。而ABS控制器是ABS裝置的核心，因而研究ABS控制器是非常必要的。目前有很多控制算法，各控制算法都有各自的利弊，當路面狀況改變時，單一控制器不利于車輛的制動。PID控制器是具有比例、積分和微分控制規律的控制器，可控制汽車在制動時的滑移率，且控制算法簡單、穩定性較好，但不能滿足汽車制動時的實際工況。模糊控制不要求控制對象具有精確模型，并有較強的適應性和魯棒性。因此，采用模糊PID控制算法能充分發揮PID控制器和模糊控制兩種算法的優點。

1 ABS的動力學建模

1.1 理論依據

汽車制動時利用的是地面與輪胎之間的摩擦，使輪速與車速之間產生速度差，這種狀態即為滑移現象。最佳車輪滑移率為15%～25%，此時汽車在制動或轉向時都可獲得較大的側向力。一般把20%稱為最佳滑移率。

1.2 車輛動力學模型

單輪車輛模型主要用于研究汽車的制動性能，可利用該模型分析ABS系統的制動問題。車輛受力分析如圖1所示。

研究單輪車輛模型制動過程時不考慮空氣阻力和滾動阻力對汽車的影響，由此可得出車輛動力學方程，其中車輛運動方程為：

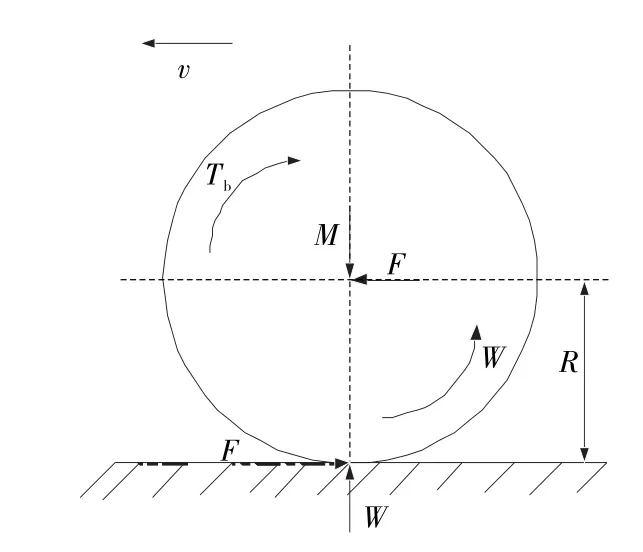
圖1 車輛受力分析示意圖

車輪運動方程為：

車輛縱向摩擦力為：

式中：M為汽車質量的1／4（kg）；v為車輛行駛速度（m／s）；F為汽車縱向附著力（N）；I為車輪轉動慣量（kg·m2）；ω為車輪轉動角速度（rad／s）；R為車輪半徑（m）；Tb為制動力矩（N·m）；μ為縱向附著系數。

由式（1）～（3）建立Simulink車輛仿真模型，以制動力矩Tb和縱向附著系數μ為輸入量，輸出量為車輪轉速ω、車輛速度v和車輛制動距離s，仿真模型如圖2所示。

1.3 輪胎模型

輪胎模型是指車輛制動時輪胎附著力與其他參數間的函數關系。除滑移率外，運行車速、路面狀況、天氣及輪胎花紋、結構等都是影響汽車行駛時附著系數的因素。但現實中大多數影響因素是變量，很難得到這些參數與附著系數的關系式。但滑移率與附著系數的關系式可以得到，可按照表達式建立

模型。采用應用廣泛的雙線性模型（如圖3所示）。

圖2 車輛動力學仿真模型

1.4 制動系統模型

制動系統包含傳動機構和制動器，制動系統模型同樣包括傳動機構模型和制動器模型。傳動機構模型采用液壓機構，為了簡化系統，不考慮其他因素的影響，主要考慮電磁閥電流與制動壓力的關系。傳遞函數為：

式中：K為環節增益；S 為電磁閥的響應時間；T為時間常數。

由于電磁閥的響應時間通常小于或等于10 ms，慣性過程的參數T取0.01，K取100。

制動器模型是指制動器力矩與制動液壓之間的關系模型。為了簡便控制算法，假定制動器的非線性特性很弱且不考慮傳送滯后的影響。制動器表達式如下：

式中：k為制動器制動系數（N·m／k Pa）；p為制動壓力（k Pa）。

由式（4）、式（5）建立的制動系統仿真模型如圖4所示。

圖4 制動系統仿真模型

1.5 滑移率計算公式

制動時車輛的滑移程度一般用滑移率表示，其計算公式見式（6），仿真模型如圖5所示。

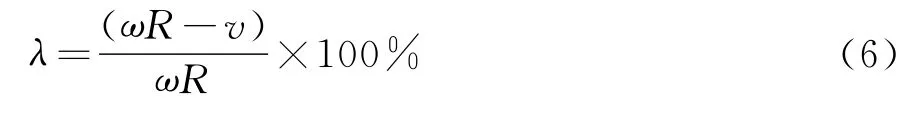
圖5 滑移率計算模型

2 模糊PID控制器設計

2.1 控制系統結構設計

模糊PID控制器的輸入量為誤差e和誤差變化率ec，要求根據不同時刻的e和ec對PID參數進行整定和修改，組成模糊PID控制器，系統結構如圖6所示。

圖6 模糊PID控制系統的結構

2.2 隸屬度函數的確定

PID參數自整定通常要求控制器為兩輸入三輸出，輸入量為誤差e和誤差變化率ec，輸出變量為ΔKp、ΔKi和ΔKd。依據經驗，定義輸入量e 和ec的范圍為［-3，3］，模糊子集為｛NB，NM，NS，ZE，PS，PM，PB｝；輸出量ΔKp、ΔKi和ΔKd的范圍為［0，1］，模糊子集為｛ZE，PO，PS，PM，PB｝。輸入、輸出隸屬函數如圖7、圖8所示。

通過調整參數ΔKp、ΔKi和ΔKd，實現系統的自適應模糊PID控制。調節計算式為：

圖7 e和ec的隸屬度函數

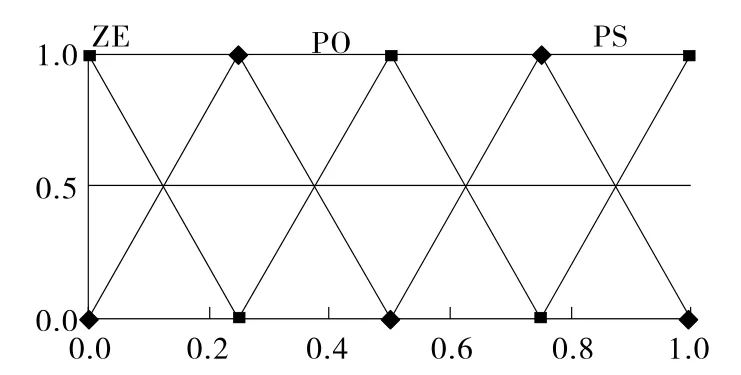
圖8 ΔKp、ΔKi和ΔKd的隸屬度函數

式中：K′p、K′i、K′d為原先整定好的PID參數。

2.3 確定模糊控制規則

通常要求Kp、Ki和Kd在不同e和ec的控制下。制動開始時e較大，應選擇較大的Kp和較小的Kd，保證系統有較好的追蹤效果，為防止系統超調過大，一般取Ki=0；當e和ec為中等大小時，為保證超調減小，選擇較小的Ki，但Kp、Kd的大小要合適；當e較小時，為保證系統有較好的穩定狀態，應增大Kp和Ki，選擇適中的Kd。ΔKp、ΔKi和ΔKd的模糊規則如表1～3所示。

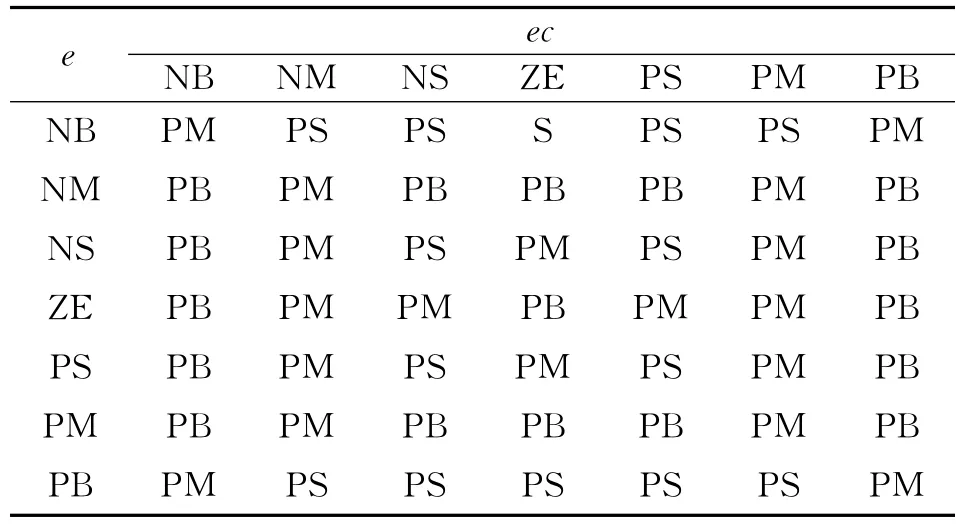
表1 ΔKp的模糊規則

表2 ΔKi的模糊規則

表3 ΔKd的模糊規則

2.4 解模糊化

按照模糊控制規則推理后，要反模糊化計算整定的3個參數，并得到輸出量。采用重心法，計算方法見式（7）。模糊PID控制仿真模型如圖9所示。

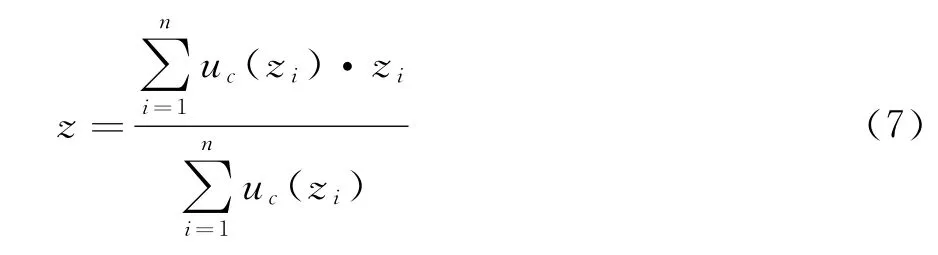
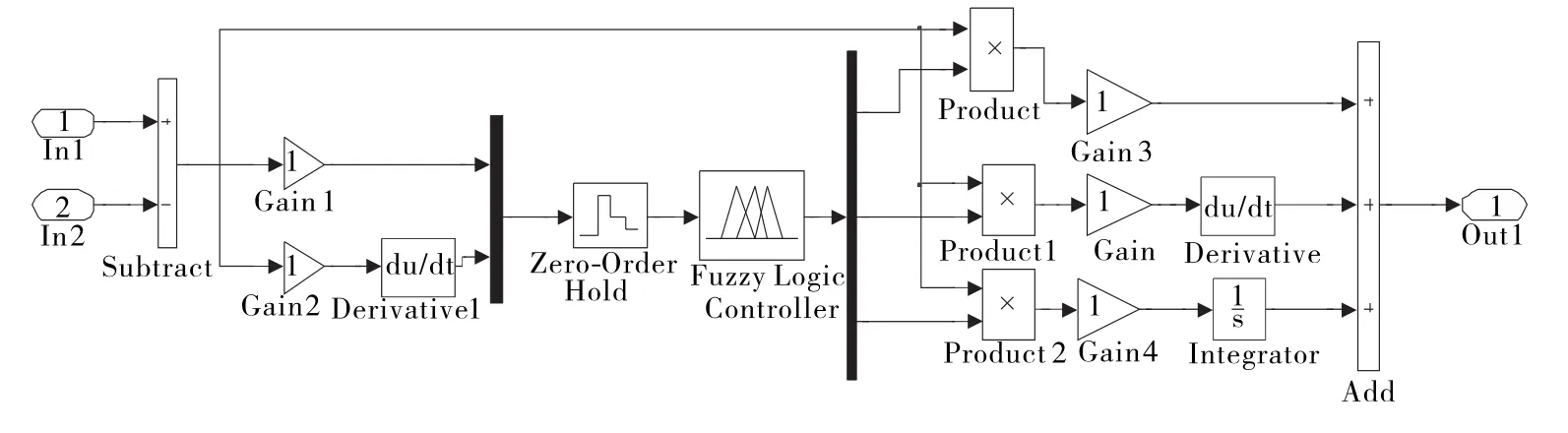
圖9 模糊PID控制仿真模型

3 ABS系統仿真及結果分析

3.1 ABS系統仿真

借助Simulink，在不同路面上對模糊PID控制的ABS進行制動仿真。以某轎車為例，初始速度取25 m／s，1／4質量M為375 kg，車輪半徑R為0.3 m，車輪轉動慣量I為4.8 kg·m2，ABS系統仿真模型如圖10所示。

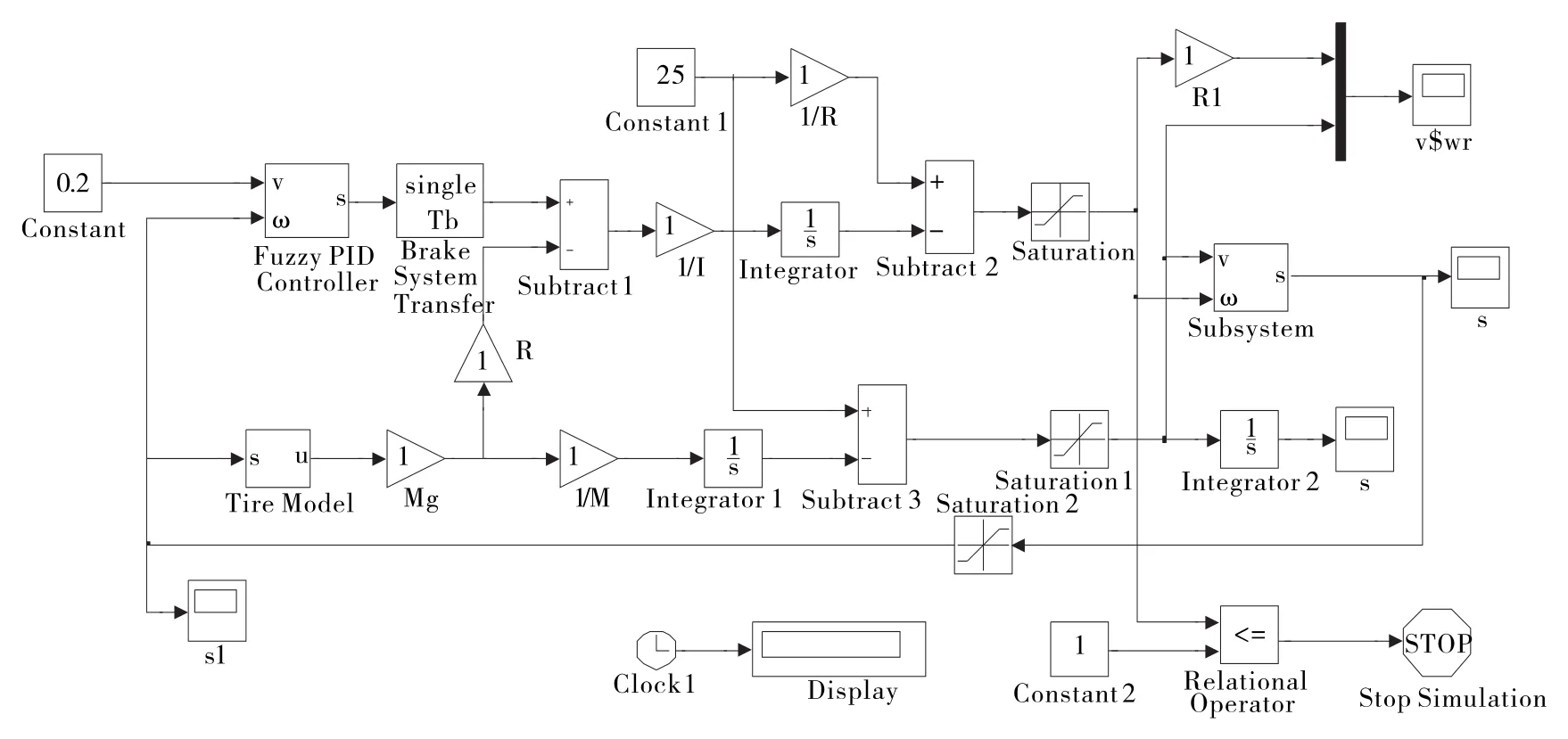
圖10 ABS系統仿真模型

3.2 仿真結果分析

在干、濕瀝青路面上分別進行車輛仿真，得到輪速、車速和滑移率的關系曲線（如圖11～13所示）。

圖11 干瀝青路面上車速和輪速曲線

圖12 濕瀝青路面上車速和輪速曲線

由圖11～13可知：1）汽車在干、濕瀝青路面上制動時，滑移率分別達到0.18、0.15附近后基本保持不變，且制動時間可達到要求，說明模糊PID控制器控制的ABS能滿足制動要求。2）模糊PID控制器控制的ABS在不同路面上雖然滑移率發生改變，但制動過程都能保持平穩，說明設計的模糊PID控制器能適應不同路面上的制動。

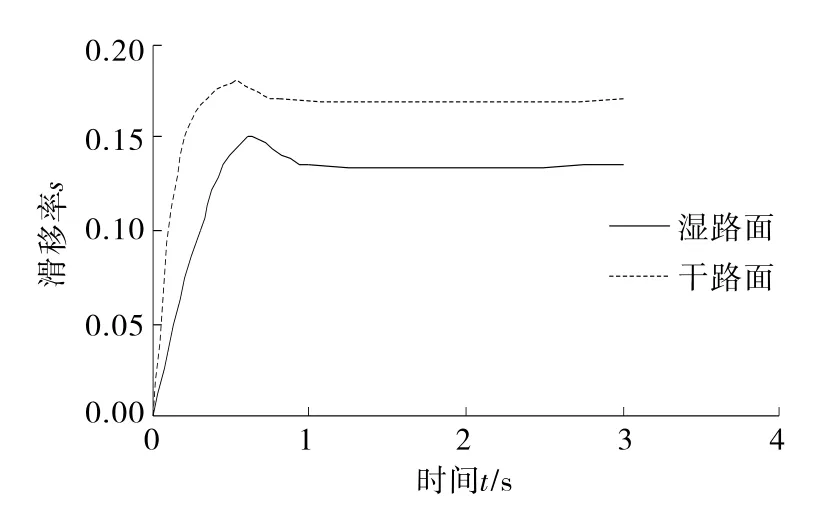
圖13 兩種路面上滑移率對比曲線

4 結論

該文借助MATLAB軟件并依據ABS控制系統的特點設計ABS模型和模糊PID控制器，仿真分析其在不同路面上的制動效果。結果表明模糊PID控制器控制的ABS在干、濕兩種路面上都可達到安全性能要求，制動過程中方向均保持穩定狀態，模糊PID控制器可適應不同的路面，而且對于優化ABS的性能有效。

［1］ 張穎，袁朝輝.汽車防抱死系統的模糊PID控制算法研究［J］.計算機仿真，2010，27（12）.

［2］ 余志生.汽車理論［M］.北京：機械工業出版社，2009.

［3］ 張振生.基于模糊PID控制的ABS仿真研究［J］.北方交通，2008（5）.

［4］ 付爾第.汽車防抱死系統建模仿真及控制方法的研究［D］.錦州：遼寧工業大學，2014.［5］ 吳玲，孫宇.基于Matlab／Simulink的汽車ABS系統建模與仿真［J］.自動化應用，2014（5）.

［6］ 席本強，何毅.汽車ABS的模糊自適應PID控制［J］.遼寧工程技術大學學報：自然科學版，2014，33（11）.

［7］ 李歡，何鋒，蔣雪生.基于模糊控制的氣電混合動力客車控制策略研究［J］.客車技術與研究，2015（1）.

［8］ 武愷航，李勇，吳旻駿，等.基于模糊控制的氣壓ABS建模方法［J］.公路與汽運，2012（6）.

［9］ 陳寧，黃會明，吳汶芪.基于模糊控制的電動汽車電子差速設計［J］.客車技術與研究，2013（3）.

［10］ 王立平，李守成，劉英杰.基于Matlab／Simulink的半掛汽車列車防抱死制動系統仿真研究［J］.拖拉機與農用運輸車，2011，38（6）.

U463.52

A

1671-2668（2016）06-0009-04

2016-05-10