波形鋼腹板梁橋腹板抗剪強度特性分析
趙磊,王濤,張興,王芳
(1.貴州大學土木工程學院,貴州貴陽 550025;2.貴州大學機械工程學院,貴州貴陽 550025)
波形鋼腹板梁橋腹板抗剪強度特性分析
趙磊1,王濤1,張興1,王芳2
(1.貴州大學土木工程學院,貴州貴陽 550025;2.貴州大學機械工程學院,貴州貴陽 550025)
基于理論計算與ABAQUS有限元軟件,對波形鋼腹板簡支梁橋腹板截面的不同彎折角度及彎折段與直線段不同長度模型進行計算,分析了波形鋼腹板梁橋腹板抗剪強度特性。結果表明,在外部荷載作用下,隨著腹板彎折角度的增大,腹板所受剪應力逐漸增大;大角度腹板可有效提高波形鋼腹板承擔豎向剪力的比例,使砼梁板受到的剪應力減小;在腹板彎折角一定的情況下,與腹板的彎折段和直線段采用等長截面形式相比,采用不等長截面形式所受剪應力較大;與波形鋼腹板相比,直腹板梁橋受力較差。
橋梁;波形鋼腹板;抗剪強度;剪應力;截面形式
波形鋼腹板與砼腹板最主要的不同在于波形鋼腹板幾乎承受主梁上的全部剪力,且剪應力大小沿梁高度方向近似相等。在相關設計中,波形鋼腹板的幾何尺寸由其抗剪強度決定,即鋼腹板上的應力應小于所選鋼材的設計抗剪強度。中國對波形鋼腹板箱梁的引進較晚,目前對它的研究處于初級階段,也只修建了為數不多的波形鋼腹板箱梁橋,其中河南衛河大橋是國內第一座將波形鋼腹板梁橋應用于高速公路的簡支橋梁。該文以該橋中跨跨度52 m簡支段作為模擬原型,取鋼腹板厚度t為10 mm,采用ABAQUS有限元數值模擬方法計算波形鋼腹板的應力,然后改變波形鋼腹板的主要幾何參數尺寸,研究各幾何參數對波形鋼腹板受力性能的影響,為波形鋼腹板梁橋腹板設計提供參考。
1 工程背景
河南衛河大橋采用簡支三跨結構,跨徑組合為47 m+52 m+47 m。橫斷面采用單箱三室直腹式等截面箱梁,梁高3.2 m,主跨高跨比為1/16.25。頂板寬16.85 m,底板寬11.85 m,翼緣板懸長2.5 m,頂板厚25 cm,頂板端部厚20 cm,底板厚22 cm(見圖1)。
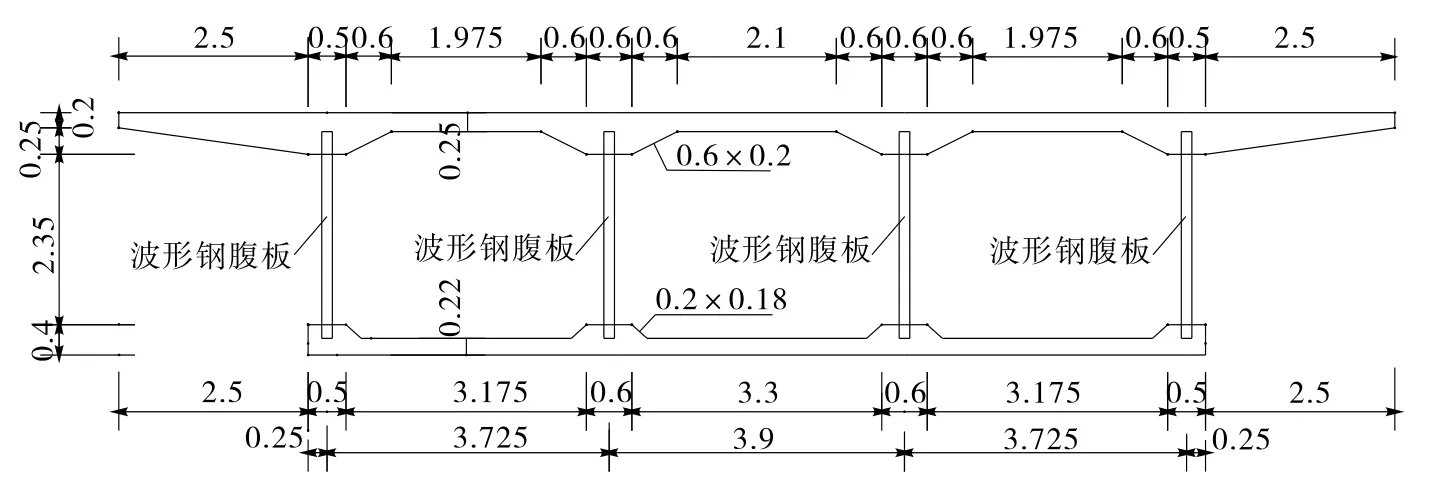
圖1 河南衛河大橋上部結構斷面圖(單位:m)
以其中跨跨度52 m簡支段為模擬原型,取箱梁頂底板砼為C50,波形鋼腹板采用Q345型鋼,設計抗拉、抗壓、抗彎應力f 為310 MPa,抗剪強度fv為180 MPa,設計采用公路-Ⅰ級荷載。波形鋼腹板主要幾何參數(見圖2)如下:一個周期波形鋼腹板的水平總長度l=1 600 mm;波形鋼腹板的直板段水平長度a=430mm;斜板段水平長度c= 370 mm;波高h=220 mm;水平折疊角β=30.7°;板厚t=10 mm;腹板高度hw=2.73 m。
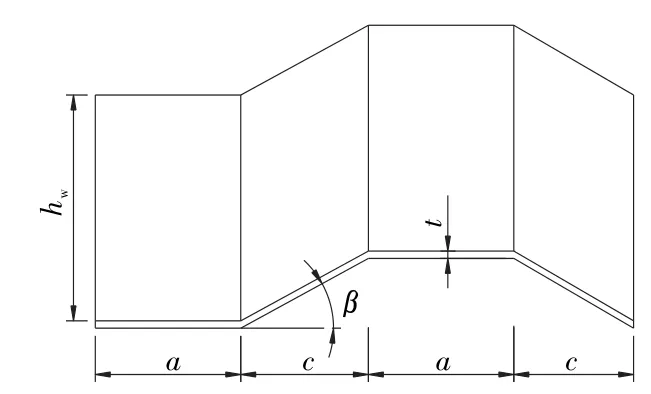
圖2 波形鋼腹板幾何參數示意圖
2 計算理論
波形鋼腹板梁橋腹板的受力以剪力為主,整座橋梁的剪力主要由腹板承擔,假定其剪力全部由腹板承擔。依據JTG D60-2015《公路橋涵通用設計規范》計算剪力效應,公路-Ⅰ級荷載集中力pk= 1.2×360 k N=432 k N,均布荷載qk=10.5 k N/m,荷載布置見圖3。由于腹板主要承擔剪力,幾乎不承擔彎矩作用,故取橋縱向剪力最大值的支點附近為計算截面,剪力影響線見圖4。
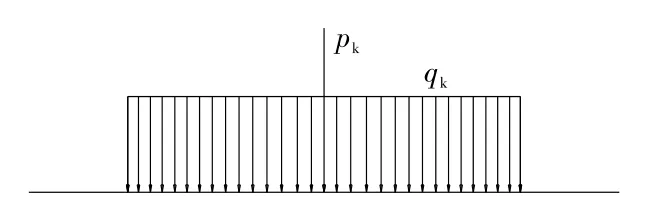
圖3 波形鋼腹板幾何參數

圖4 支點附近剪力影響線
由于ABAQUS中已考慮結構自重作用效應,在依據規范計算支點剪力效應過程中只需計算可變作用作為基本組合效應的設計值Sud,取安全等級為二級,且采用車道荷載計算,則結構重要性系數γ0=1,γQ1=1.4。對于52 m簡支梁橋,根據影響線布置荷載得:假定剪力全部由波形鋼腹板承擔,考慮支點橫隔板整面約束作用效應,支點的各片梁組成的整體截面剪應力強度近似采用基本公式計算:
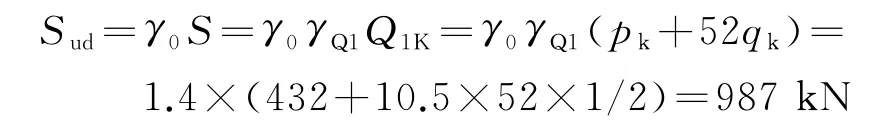
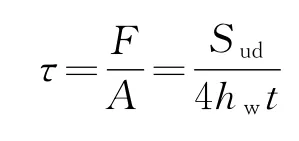
3 腹板不同彎折角度模型計算分析
3.1 腹板彎折角度30.7°
取腹板水平折疊角β=30.7°,板厚t=10 mm,腹板高度hw=2.73 m(見圖5)。采用Solid三維實體單元建立模型,單元計算網格采用C3D8R三維六面體二次減縮元。砼彈性模量為34.5 GPa,泊松比為0.2;型鋼彈性模量為206 GPa,泊松比為0.3。邊界采用鉸支約束,采用公路-Ⅰ級荷載加載。模型計算結果見圖6。在ABAQUS有限元軟件中,坐標軸1、2、3方向分別代表坐標x、y、z軸,剪應力τ= τyz即為橋梁橫截面向上或向下方向的剪應力S23。
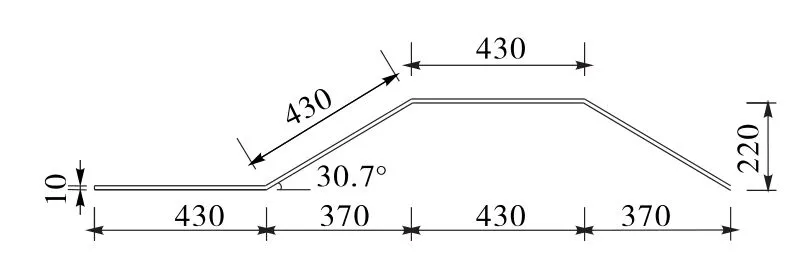
圖5 腹板彎折角度為30.7°單周期截面尺寸(單位:mm)
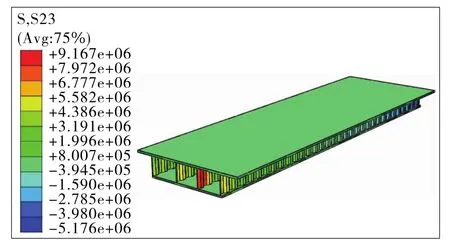
圖6 腹板彎折角度30.7°有限元模型計算結果(單位:Pa)
腹板厚度t=10 mm時,理論抗剪強度為:

根據圖6,τmax=S23max=9.17MPa,與理論計算值基本吻合。
3.2 腹板彎折角度60°
腹板彎折角度取60°進行模型分析計算,腹板截面見圖7,其中砼頂、底板及尺寸、腹板厚、高度、材料強度等材料條件同3.1節。計算結果見圖8。

圖7 腹板彎折角度60°單周期截面尺寸(單位:mm)
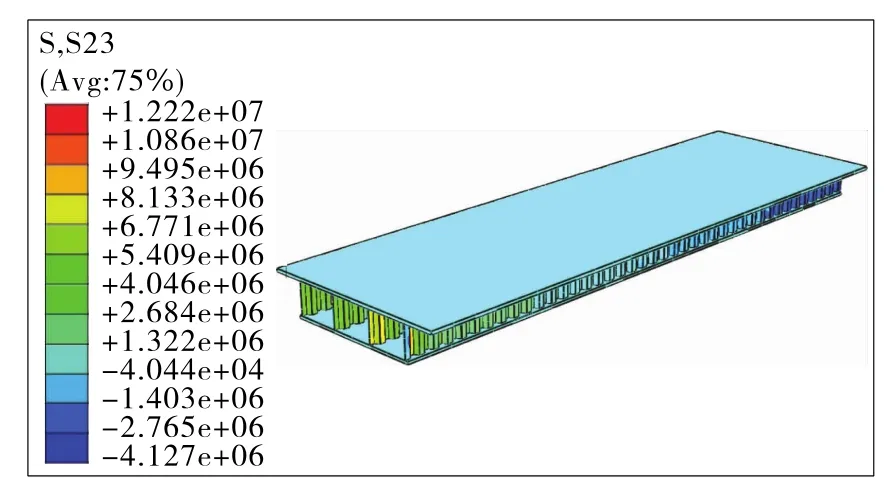
圖8 腹板彎折角度60°有限元模型計算結果(單位:Pa)
根據圖8,τmax=S23max=12.22MPa。與彎折角
度30.7°的波形鋼腹板梁橋相比,60°彎折角度的波形鋼腹板承擔了更大部分豎向剪力,與前者相比,60°彎折角度腹板的砼頂、底板所受到的豎向剪力顯著減小。
3.3 腹板彎折角度0°(直板)
腹板彎折角度取0°進行模型分析計算,腹板截面直接由波形變換為平直鋼板,厚度取10 mm;砼頂、底板及尺寸、腹板高度、材料強度等材料條件同3.1節。計算結果見圖9。
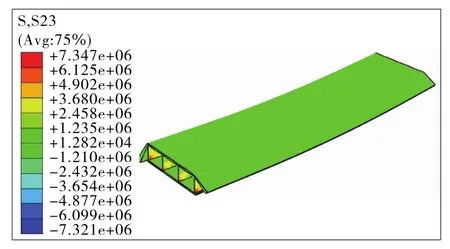
圖9 腹板彎折角度0°時有限元模型計算結果(單位:Pa)
根據圖9,τmax=S23max=7.35MPa,說明0°彎折角度的腹板只承擔了小部分豎向剪力,且橋梁發生了整體屈曲,雖然腹板剪應力較小,但受力情況極差。
3.4 不同彎折角度模型計算結果分析
波形鋼腹板梁橋腹板不同彎折角度模型計算結果見表1。
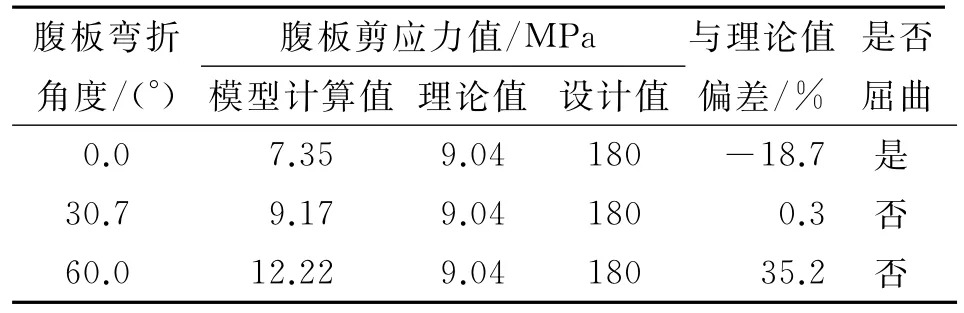
表1 腹板剪應力與彎折角度
從表1可以看出:在外部荷載作用下,隨著腹板彎折角度的增大,腹板所受剪應力逐漸增大,其函數關系近似為線性關系;30.7°彎折角度腹板的受力較接近理論計算結果;60°彎折角度腹板承擔的豎向剪力相對較多,使砼分擔的剪力顯著減小,證明大角度腹板能提高波形鋼腹板分擔豎向剪力的比例,使砼承擔更小的剪力;直腹板梁橋在型鋼材料遠未達到設計抗剪強度時即發生屈曲破壞,與波形鋼腹板相比,直腹板梁橋受力較差。為了使波形鋼腹板在屈曲之前更能發揮抗剪強度,可以考慮設計適中的腹板彎折角度。
4 彎折段和直線段不同長度模型計算分析
4.1 折減彎折段長度模型計算
對波形鋼腹板梁橋1 600 mm型腹板彎折部分進行長度折減,取原長度的一半即215 mm作為彎折段長度進行模型計算,材料、尺寸、角度等其他指標同3.1節。腹板截面見圖10,計算結果見圖11。

圖10 斜腹板為215 mm單周期截面尺寸(單位:mm)
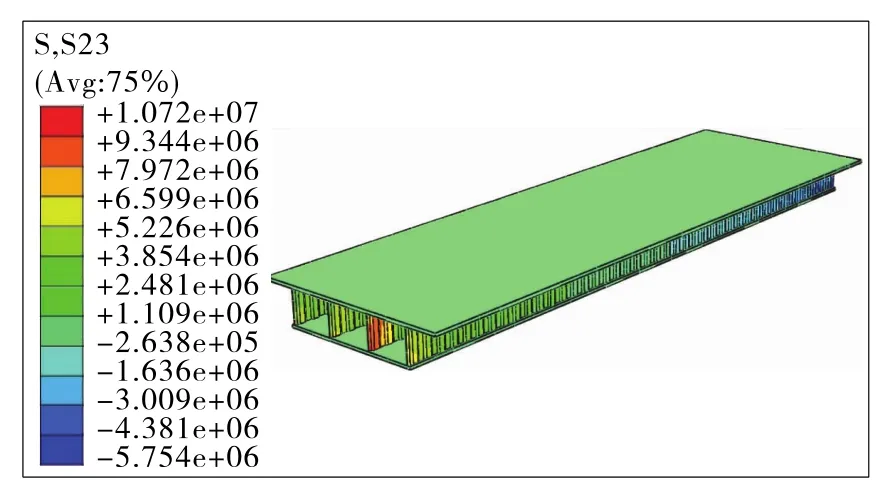
圖11 斜腹板為215 mm有限元模型計算結果(單位:Pa)
根據圖11,τmax=S23max=10.72MPa。與斜腹板為430 mm波形腹板相比,215 mm斜腹板波形腹板承擔了更大的豎向剪力,與前者相比,215 mm長斜腹板波形腹板受到的剪應力較大,受力情況較差,偏于危險。主要原因為減小腹板彎折段長度相當于減小腹板波高,使波形板的受力逐漸趨近于直板形式,其截面受力情況與直板極為相似,而且可以大膽推測,當腹板的波高逐漸減小時,腹板應力將逐漸增大,橋體將逐漸出現局部及整體屈曲,其受力趨近于直板截面屈曲形式。因此,在設計中不可使腹板相對波高過小,要特別注重波形鋼腹板梁橋腹板彎折段長度或波高的計算及取值。
4.2 折減直線段長度模型計算
對3.1節中的腹板直線部分進行長度折減,取原長度的一半即215 mm作為直線段長度進行模型計算,材料、尺寸、角度等其他指標同3.1節。腹板截面見圖12,計算結果見圖13。
根據圖13,τmax=S23max=9.91MPa,與斜腹板長度為215 mm的波形腹板相比,這種形式腹板應力偏小,但橋梁發生了整體和局部屈曲;與斜腹板長度為430 mm的波形腹板相比,這種形式腹板剪應
力相對較大,受力情況較差。為了不使波形鋼腹板梁橋過早發生屈曲,在設計中不可使腹板相對波高過大,要特別注重波形鋼腹板梁橋腹板直線段長度選取和計算。
前幾天,我和幾個同學聚會,十多年未見面了,大家都異常興奮,在茶香氤氳的包間里,彼此親切地詢問著對方的近況。多年不見,昔日青澀懵懂的學友,如今都已成熟睿智,我們談起了各自的生活,都想從別人那里尋找一些幸福感。
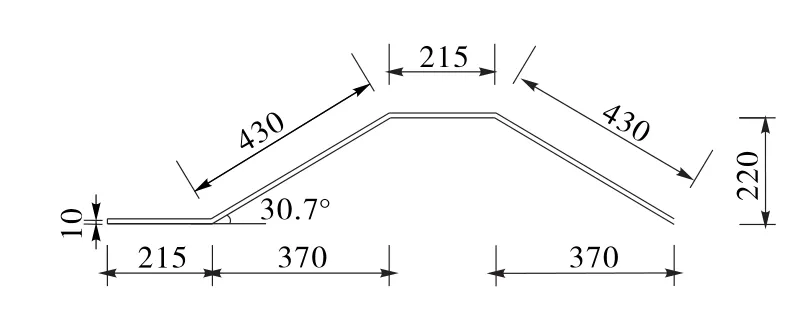
圖12 直腹板為215 mm單周期截面尺寸(單位:mm)
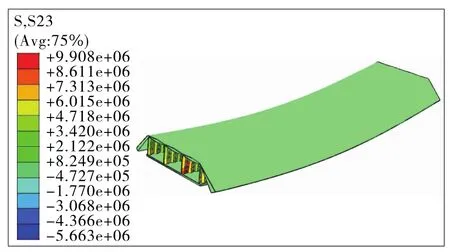
圖13 直腹板為215 mm有限元模型計算結果(單位:Pa)
4.3 腹板截面單周期800 mm模型計算
取3.1節中波形鋼腹板單周期長度1 600 mm的一半即800 mm,使腹板截面各部分長度均減到一半,并保持板厚度10 mm不變,以此作為波形鋼腹板單周期長度進行模型計算,材料、尺寸、角度等其他指標同3.1節。腹板截面見圖14,計算結果見圖15。
根據圖15,τmax=S23max=7.42MPa,相比于腹板單周期長1 600 mm各種類型受力情況,腹板單周期長800 mm波形鋼腹板梁橋所受剪應力更小,頂、底板砼所受剪應力也更小,腹板受力情況更好,主要是因為腹板剪應力分布沿橋縱向更為均勻、合理。因此,要特別注重波形鋼腹板梁橋腹板單周期長度的計算及取值。

圖14800 mm單周期截面尺寸(單位:mm)
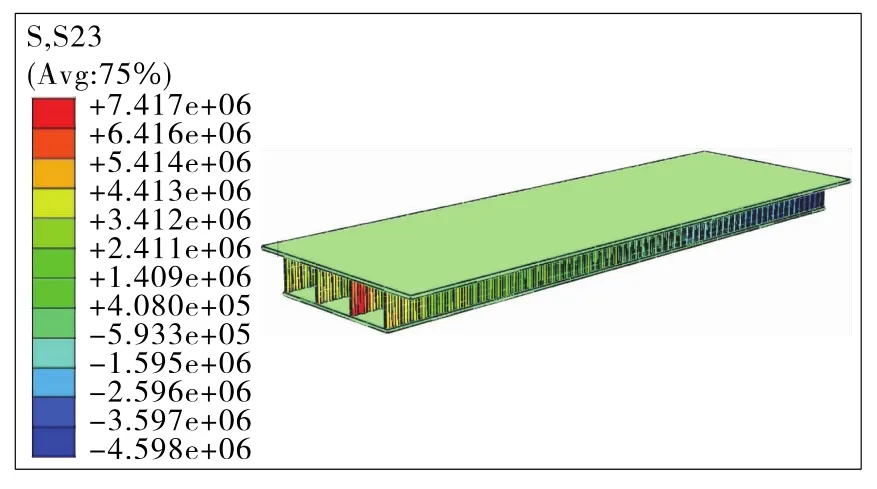
圖15 腹板單周期800 mm有限元模型計算結果(單位:Pa)
4.4 彎折段和直線段不同長度模型結果分析
波形鋼腹板梁橋腹板彎折段、直線段不同長度模型的計算結果見表2。

表2 腹板剪應力與彎折段、直線段長度
從表2可看出:在不改變腹板彎折角30.7°的情況下,當腹板彎折段、直線段長度采用不等長的截面模型時,腹板所受剪應力增大;彎折段、直線段長度均為430 mm的波形鋼腹板所受剪應力最接近于理論計算值;彎折段、直線段長度均為215 mm的波形鋼腹板所受剪應力最小。直線段與彎折段長度不相等的波形鋼腹板在外荷載作用下受到的豎向剪應力比彎折段、直線段等長波形鋼腹板更大,從而產生屈曲,承載能力不如彎折段、直線段等長的波形鋼腹板。設計時應優先選用彎折段、直線段等長的結構形式,并重點計算和選用腹板單周期長度。
5 結論及建議
(1)在外部荷載作用下,隨著腹板彎折角度的增大,腹板所受剪應力逐漸增大,其函數關系近似為線性關系。
(2)對于52 m波形鋼腹板簡支梁橋,采用單板周期1 600 mm,彎折角度30.7°,彎折段、直線段長度均為430 mm的波形鋼腹板其受力較接近理論計算結果。
(3)60°彎折腹板承擔的豎向剪力相對較大,砼頂、底板承擔的剪力相對減小,證明大角度腹板能提高波形鋼腹板承擔豎向剪力的比例,使砼梁板受到的剪力減小。
(4)直腹板梁橋在型鋼材料遠未達到設計抗剪強度時即發生屈曲破壞,與波形鋼腹板相比,直腹板梁橋受力較差,建議不采用0°直腹板形式。為了使波形鋼腹板在屈曲之前更能發揮抗剪強度,可考慮設計適中的腹板彎折角度。
(5)在腹板彎折角為30.7°的情況下,當腹板彎折段、直線段長度采用不等長的截面模型時,腹板所受剪應力顯著增大,且腹板斜邊段相對較大的腹板截面形式受力較大,腹板直線段相對較短的腹板截面形式雖然受力較小但更容易發生屈曲。說明直線段與彎折段長度不等的波形鋼腹板在外荷載作用下受到的豎向剪應力比彎折段、直線段等長波形鋼腹板更大,較易屈曲,受力情況差。設計中建議不選用彎折段、直線段長度不等的波形鋼腹板截面形式。
(6)彎折段、直線段長度均為215 mm的波形鋼腹板所受剪應力最小,彎折段、直線段長度均為430 mm的波形鋼腹板所受剪應力次之。設計時建議優先選用彎折段、直線段等長的結構形式,并根據工程特點重點計算和選用波形鋼腹板單周期長度。
[1] 陳寶春,黃卿維.波形鋼腹板PC箱梁橋應用綜述[J].公路,2005(7).
[2] 朱越峰,吳樸,謝旭,等.部分波形鋼腹板箱梁受力特性分析[J].浙江大學學報:工學版,2008,42(1).
[3] GB 50017—2003,鋼結構設計規范[S].
[4] JTG D60—2015,公路橋涵通用設計規范[S].
[5] JTG D62—2004,公路鋼筋混凝土及預應力混凝土橋涵設計規范[S].
U448.21
A
1671-2668(2016)06-0165-05
2016-06-10

