水平軸潮流能水力渦輪數值模擬與試驗研究
肖云峰,高鵬遠,黃俊強,王 信,鄒文昊
(1.北京石油化工學院,北京 102617;2.北京化工大學,北京 100029)
水平軸潮流能水力渦輪數值模擬與試驗研究
肖云峰1,高鵬遠2,黃俊強1,王信1,鄒文昊1
(1.北京石油化工學院,北京102617;2.北京化工大學,北京100029)
首先,使用葉素動量理論對所設計的室內試驗用小型水平軸潮流能水力渦輪葉片模型進行初步計算,獲得其性能參數,此后借助NUMECA軟件,采用三維計算流體動力學(CFD)方法對水平軸水力渦輪進行三維水動力分析,得到其性能曲線,最后通過試驗水槽進行模型試驗,對BEM計算結果和CFD計算結果進行驗證,結果表明:葉素動量理論和CFD方法均能對水力渦輪性能進行有效預測,且CFD方法具有更高的精度;此外,根據CFD方法得到葉片表明的壓力分布,根據空化條件可知,該水力渦輪會發生空化。
BEM;CFD;水動力性能;空化;實驗
21世紀以來,隨著科技的發展和人口的增長,傳統能源如煤、石油、天然氣緊缺的問題日漸凸顯。目前,我國石油消費量居世界第二,超過50%依賴進口。積極開發與研究新型能源,消除我國能源隱患,使能源結構合理化已經成為大勢所趨[1]。潮流能作為一種新能源,具有蘊藏能量大、綠色環保的特點,在不占用陸地空間的同時,可以實現資源綜合利用,這正好彌補了常規化石能源的不足之處。此外,隨著化石能源等不可再生能源的日益減少以及對環境的保護要求越來越高,如何有效開發利用潮流能引起各國的高度重視。在海洋能的開發利用領域中,潮流能的開發利用已變得最為活躍[2]。
潮流能發電裝置的核心裝備為水力渦輪,其作用就是將海水的動能轉化為葉輪的機械能,各國研究人員開發了多種不同形式水力渦輪。其中水平軸潮流能水力渦輪具有效率高、技術相對成熟的特點,同時可以借鑒水平軸風力機開發利用的經驗,是具有較好應用前景的形式,在目前的潮流能開發裝置中占到很大份額。筆者以自行設計的20 W潮流能水力渦輪為例,基于Qblade二維計算軟件和NUMECA流體三維模擬軟件,對所設計的葉片進行水動力性能計算,并將計算結果與實驗結果進行對比。
1 理論基礎
1.1葉素動量理論
當前國內外計算風力機葉片氣動性能的理論有貝茨理論、動量理論、葉素理論、葉素動量理論[3-4]等。其中,葉素動量理論結合了動量理論和葉素理論,計算出風輪掃掠面中的迭代變量軸向誘導因子a和周向誘導因子b。如圖1所示,風輪流動模型簡化為一個理想的單元流管,并將其離散成N個高度為dr的環形單元,單元之間沒有流動。

圖1 葉素動量理論單元流管模型
由動量理論可得到作用在dr微段上的推力及轉矩:


通過葉素理論可以得到作用在dr微段的推力與轉矩:
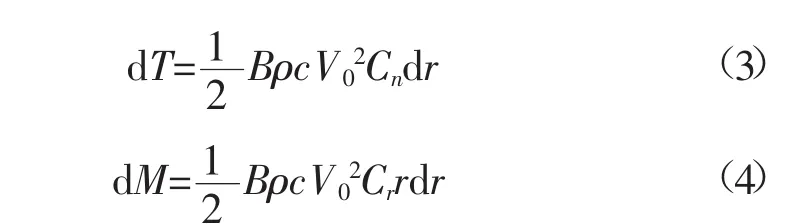
由葉素理論和動量理論得出的推力和轉矩相等,并由速度三角形可得:
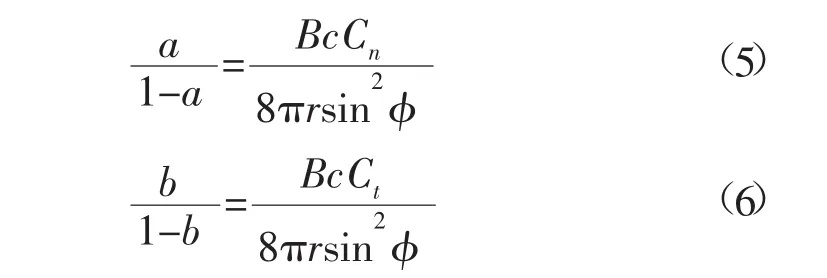
1.2CFD基本理論
NUMECA公司的FINE/TURBO軟件包具有十分強大的流場計算和前后處理功能。FINE/TURBO采用時間相關法求解雷諾平均的N-S方程,離散方式為中心節點的有限體積法,以顯示四階RUNGEKutta法求解,并具有多重網格初場處理和多重網格迭代加速以及低流速的預處理技術。湍流模型為一方程Spalart-Allmaras(S-A)模型。
1.3葉片模型
水力渦輪為水平軸三葉片定槳型,葉片半徑0.19 m,額定功率20 W,葉尖速比為3,設計流速為1 m/s,葉片旋轉軸為Z軸。

圖2 葉片模型
1.4計算域和網格
與風力機相同,水力渦輪計算域包括內部流動域和外部繞流域,計算域的精準程度關乎計算結果的準確程度,因此,必須嚴格把握計算域。根據水力渦輪實際工作情況確定計算區域包括葉片旋轉平面,進口段和出口段,其中葉片展向延伸到3倍半徑(3R),考慮到水力渦輪下游尾流的影響葉片下游尺寸為5倍葉高,上游也設定為5R。
計算網格通過Igg/AutoGrid模塊生成,如圖3所示,由于葉片流道具有周期性,因此只需給出單列網格。最終生成的網格單列網格總數約為83萬,無負網格,流道最小網格正交性為16.149,遠場最小網格正交性為 16.218,流道最大長寬比為767.39,遠場為2 583.6,流道最大延展比2.976 4,遠場為2.611 2。網格質量符合計算要求。
比如,2005年起,石化銷售系統開始逐步實現增值稅市級集中繳納,因各市、區縣財政收入不均衡,導致市級集中納稅多沒有得到地方認可,所以部分公司一直按各自經營所在地收入比例在當地入庫繳納增值稅,其中依此計算的城建稅比例縣區是5%、市區是7%,相差兩個百分點,如果完全集中繳納,這兩個百分點的納稅幅度累積下來也是不小的開支。所以,涉及企業完全可以在稅源不是十分緊張的情況下,利用各級稅種的稅負差別,逐漸減少或不實行集中納稅,放歸稅源所在地繳納,如果有減免或稅收優惠政策的,可加以利用集中繳納,盡量把幾個百分點的減稅或增收作用利用起來。

圖3 網格示意圖
進口邊界條件:給定水流軸向流速、靜溫以及湍流粘性。出口邊界條件設定壓力出口,輪轂可設定為Euler壁面,葉片表面設定為粘性壁面。當計算殘差下降三個量級以上,總體性能參數達到穩定認為收斂。
2 結果討論
2.1性能分析
根據CFD理論計算的額定工況下水力渦輪性能結果如圖4所示,在葉尖速比為3時,葉片功率系數達到最大值0.353 471,略大于設計點。與BEM方法計算結果比較,獲能系數和推力系數變化趨勢基本一致,而獲能系數曲線最高點左移,最大值有所下降,推力系數最大值也有所下降,這是因為葉素動量理論計算過程中忽略了葉尖損失、葉根損失等因素的影響。在葉尖速比為3時達到最大值,且獲能系數均超過0.35,而當水流速度增大時,獲能系數增大,因此在合理范圍內增大流速會使水力渦輪的性能有所提升,這對水力渦輪在實際運用中有很好的指導作用。
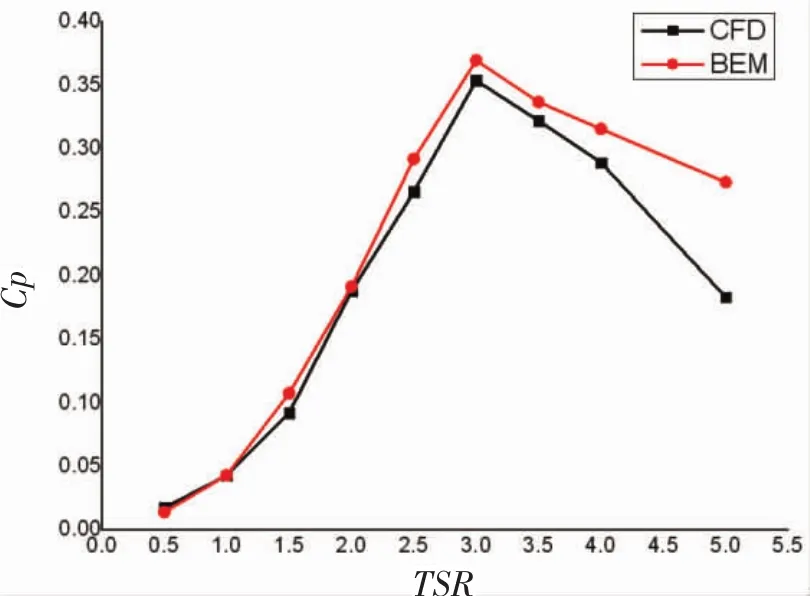
圖4 額定工況下功率系數和推力系數隨葉尖速比變化趨勢
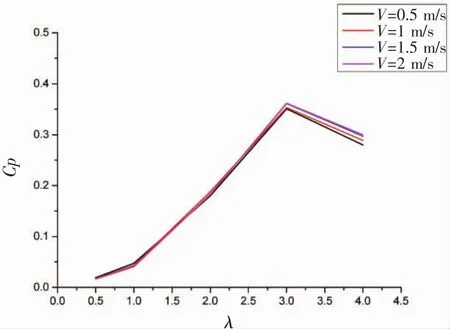
圖5 不同流速下的功率系數
2.2空化分析
空化現象經常發生在水力渦輪運行過程中,空化的產生對水力渦輪性能產生嚴重影響[5]。空化是指水流沖擊水力渦輪葉片時,葉片吸力面產生負壓,低于一定壓力(氣化壓力)時,葉片表面形成氣泡,由于壓力過低,氣泡越來越大,氣泡破裂后對葉片形成沖擊,影響水力渦輪性能,由于累積作用,嚴重時會對水力渦輪葉片造成損壞,因此研究水力渦輪的空化十分必要。
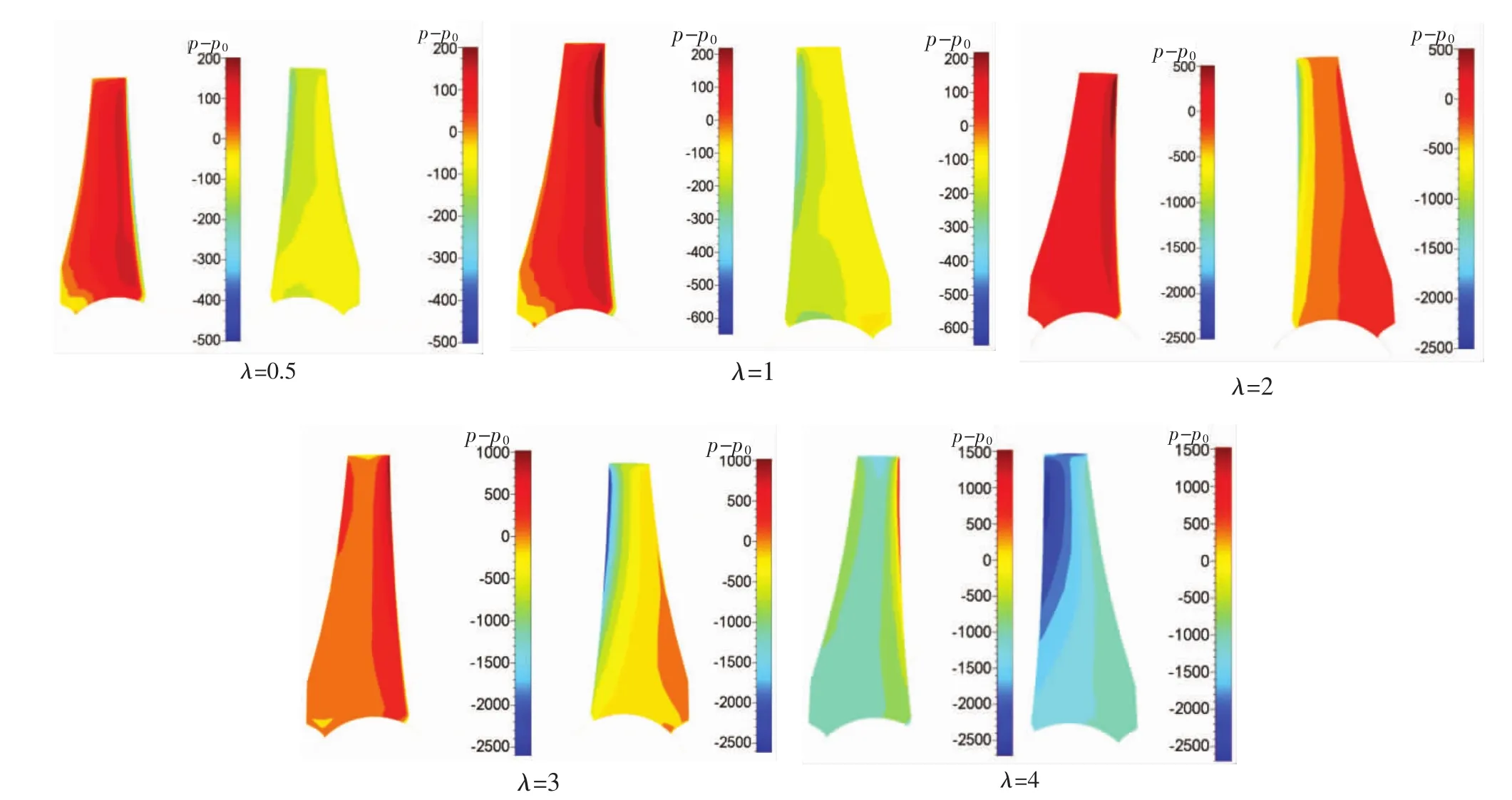
圖6 不同葉尖速比下葉片表面壓力分布
空化系數是用于判斷空化是否發生的一個重要表征,對比葉片表面壓力系數與空化系數的大小可以判斷空化是否發生。空化數為:

式中:p0為葉片截面靜壓;PV為水氣化壓力;
對比各截面壓力與20℃水的氣化壓力值可知,各截面壓力均小于水氣化壓力值,因此會發生空化,隨著轉速的增加,葉片最小壓力值進一步減小,空化現象更加嚴重。因此對于控制葉片空化可以從降低轉速入手[6-7]。

表1 不同尖速比下吸力面最低壓強

表2 水在不同溫度下的氣化壓力值
3 試驗研究
根據設計葉片的具體參數,利用數控加工進行葉片制作。借助實驗室自行搭建的敞開式試驗水槽進行試驗,試驗儀器包括:水泵、變頻器、扭矩傳感器、發電機交直流功率測量儀以及流速測量儀[7]。

圖8 試驗水槽

圖9 試驗葉片

圖10 試驗過程
3.1葉片性能實驗
葉片性能實驗有兩個目的:一是驗證所設計的葉片性能是否滿足要求;二是驗證利用BEM方法和CFD方法計算結果的正確性。
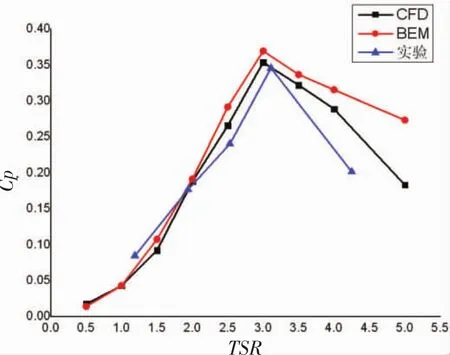
圖11 水力渦輪性能曲線
圖11為三葉片水力渦輪分別通過實驗、BEM方法和CFD方法得到的性能曲線。由圖11可知,BEM和CFD方法的計算值與試驗值變化基本趨勢一致;通過BEM和CFD方法得出的結果,在尖速比為3時功率系數取得最大值,其中CFD方法所得結果為0.353 47,BEM方法所得為0.369 31;而實驗所得最大功率系數在葉尖速比為3.11處,功率系數為0.345 5,試驗值與計算值接近;在葉尖速比為2~4之間,試驗值比計算值小,這是由于計算選取較為理想的環境,忽略了葉尖以及葉根損失,同時,由于測量方法的局限性,實驗中各種傳動結構的能量損失也被計算在內,因此造成試驗值相比計算值偏低。但是通過對比曲線可以看出,BEM方法和CFD方法都能作為預測水力渦輪性能的理論方法。
3.2不同葉片數水力渦輪性能實驗
將葉片數增加至6,測得其性能,并與三葉片實驗結果以及BEM方法的計算結果相對比。
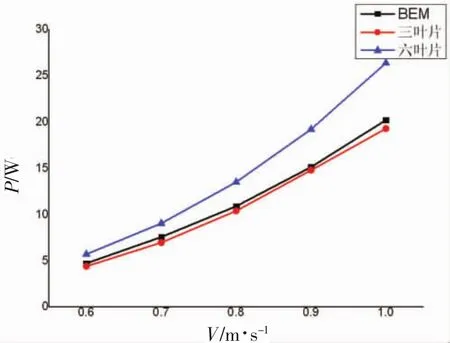
圖12 不同葉片數功率隨流速變化的曲線
從圖12中可以看出:BEM方法對三葉片水力渦輪不同流速工況預測的值與試驗結果變化趨勢一致,實驗值略小于計算值,原因如上節所描述,這是實驗中的各種損失造成的;通過對比不同葉片數的功率曲線可以看出,葉片數的增多使得水力渦輪的整體獲能性能上升,對于提高水力渦輪的性能有幫助。
4 結論
根據計算結果分析可得以下結論:
(1)采用BEM理論和三維CFD理論計算所得的水力渦輪葉片功率曲線與實驗所得結果變化趨勢基本一致。BEM方法和CFD方法均能作為水力渦輪性能預測的理論方法。
(2)BEM方法計算所得結果相比CFD方法計算結果偏大,這是由于BEM方法忽略了葉尖損失和葉根損失的影響,但是其計算速度是CFD方法所不能比的。因此,BEM方法作為快速預測水力渦輪性能的方法是可取的。
(3)不同流速下水力渦輪性能基本保持一致,流速增大時,葉輪獲能系數有所提高,因此在合理范圍內增大水流速度對葉片性能有所提高。
(4)水力渦輪葉片會發生空化現象,葉尖區域相比葉根更容易發生空化,轉速越高,空化現象越嚴重。因此,可以采用降低轉速和加大葉片翼型的厚度和彎度方法,減少空化的發生。
[1]史丹,劉佳駿.我國海洋能源開發現狀與政策建議[J].中國能源,2013,35(9):6-11.
[2]Fraenkel P.Tidal Current Energy Technologies[J].Marine Current Turbines Ltd.Ibis,2006,148:145-151.
[3]Noda M,Flay R G J.A Simulation Model for Wind Turbine Blade Fatigue Loads[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,83(1/3):527-540.
[4]Maalawi K Y,Badawy M T S.A Direct Method for Evaluating Performance of Horizontal Axis Wind Turbines[J].Renewable& Sustainable Energy Reviews,2001,5(2):175-190.
[5]江帆,黃鵬.Fluent高級應用與實例分析[M].北京:清華大學出版社,2010.
[6]辛曉鵬.水平軸海流能發電機械水動力性能的研究[D].杭州:浙江大學,2010.
[7]應有,李偉,劉宏偉,等.海流能發電裝置葉片性能及氣蝕研究[J].風機技術—試驗研究,2008,4:8-19.
[8]王儉超.水平軸潮流水輪機葉片設計和模型試驗研究[D].青島:中國海洋大學,2011.
Numerical Simulation and Experimental Study on a Horizontal Axis Tidal Current Hydraulic Turbine
XIAO Yun-feng1,GAO Peng-yuan2,HUANG Jun-qiang1,WANG Xin1,ZOU Wen-hao1
1.Beijing Institute of Petrochemical Technology,Beijing 102617,China; 1.Beijing University of Chemical Technology,Beijing 100029,China
This paper uses the blade momentum theory to calculate the parameters of a small-scale horizontal axis hydraulic turbine for laboratory test to obtain its performance.With the NUMECA software,the three-dimensional computational fluid dynamics(CFD)method is adopted for 3-D hydrodynamic analysis on the horizontal hydraulic turbine,so as to derive the power curve.Finally,a model experiment is carried out in the experimental water tank,and the results of BEM and CFD calculation are verified,showing that both the momentum theory and CFD method can effectively predict the performance of the hydraulic turbine,and the CFD method is more accurate.In addition,the pressure distribution of the blade is obtained through the CFD method.According to the cavitation conditions,cavitation can occur on the hydraulic turbine.
BEM;CFD;hydrodynamic performance;cavitation;experiments
P743;TK73
A
1003-2029(2016)05-0080-05
10.3969/j.issn.1003-2029.2016.05.016
2016-04-18
肖云峰(1976-),男,副教授,主要從事特種葉輪機械設計與研發。E-mail:xiaoyunfeng@bipt.edu.cn

