不同炮孔直徑爆破振動頻帶能量特征小波分析?

徐榮文，梁 虎，吳從師

(長沙理工大學土木與建筑學院，湖南長沙 410114)

不同炮孔直徑爆破振動頻帶能量特征小波分析?

徐榮文，梁 虎，吳從師

(長沙理工大學土木與建筑學院，湖南長沙 410114)

結合某高鐵站爆破振動實測數據，分析不同炮孔直徑對爆破地震效應的影響，對爆破振動控制具有一定意義。利用小波分析方法，獲得了不同直徑炮孔爆破振動信號的頻帶特征參數。研究結果表明：不同炮孔直徑的爆破振動信號成分主要分布在31.25～250 Hz中高頻范圍內，小孔徑炮孔的主頻高于大孔徑的主頻；小孔徑炮孔的低頻成分所占比例小于大孔徑炮孔，且隨爆心距增加，兩種孔徑的低頻成分都有增加趨勢；大孔徑爆破與小孔徑爆破相比，爆破振動能量衰減慢、振動持續時間長；采用小孔徑、多數量炮孔布置對降低爆破振動能量有一定效果。

爆破振動；炮孔直徑；小波分析；頻帶能量

爆破振動控制一直是工程爆破領域研究的重要課題之一，國內外眾多學者對爆破振動進行了大量的研究和探索。國內主要以薩道夫斯基公式為基礎進行振動速度預測，我國《爆破安全規程》也將爆破振動頻率作為參考依據之一。影響爆破振動的因素很多，在地質條件方面，有巖體條件、場地條件、爆源相對位置等；在爆源條件方面，有爆破夾制作用、炮孔布置(孔徑、孔深、排距等)、裝藥結構等。為了同時考慮更多的影響因素，能夠綜合反映爆破振動衰減規律的公式。盧文波和W.Hustrulid[1]以柱面波理論、球面波以及長柱狀裝藥的子波理論為依據，推導出質點振動速度衰減公式。在此基礎上，李洪濤[2]還推導出爆破振動能量衰減公式，并通過實測數據分別對多種爆破振動影響因素進行研究。還有許多學者集中于研究最大段藥量、爆心距、微差雷管段位等因素對爆破振動信號能量特征的影響[3-6]。在露天深孔爆破方面，關于炮孔孔徑對爆破振動影響的研究不多。雖然孔徑對爆破振動影響不是決定性因素，但也會有一定的影響，本文結合實際工程的實測數據，利用小波分析的方法，對不同爆破孔徑爆破地震波能量分布特征進行分析討論。

1 爆破振動信號現場實測

1.1 爆區概況

某高鐵站建設需采用爆破方式開挖，現場都為不規則的臺階爆破，其中分為76 mm和90 mm兩種孔徑爆破。直徑為76 mm的炮孔，孔深4～9 m，孔數布置為26～45個，最大段藥量36～76 kg，總藥量260～360 kg；直徑為90 mm的炮孔，孔深3～10 m，孔數布置為15～36個，最大段藥量27～48 kg，總藥量144～288 kg。組與組之間的微差間隔時間75 ms，均采用孔內7段導爆管雷管起爆；孔外3段導爆管雷管組成兩接力式起爆網路；均采用耦合裝藥結構，炮孔填塞長度0.5～1 m。選用2＃巖石乳化炸藥，藥卷直徑為32 mm。

1.2 現場監測方案

此次爆破振動監測中，均采用加拿大Instantel公司Minimate Pro型測振儀監測，每個測點可測垂直向、水平縱向和水平橫向的振動速度和振動頻率。

考慮距爆區較近的居民住宅區安全，測點主要布置在居民住宅區內。每次爆破布置5～6個測點，結合爆破地震波的傳播特性，測點盡可能布置在同一直線上，并且盡量避開溝槽及巖體破碎帶。

1.3 實測爆破振動信號及Fourier分析

對直徑76 mm炮孔和直徑90 mm炮孔分別進行了3次爆破振動監測和5次爆破監測，選取一組炮孔直徑不同、最大段藥量和總藥量相近、炮孔數量相同的爆破振動信號；另一組炮孔直徑、最大段藥量和總藥量、炮孔數量都不同的爆破振動信號。監測的爆破信號的條件如表1、表2所示。

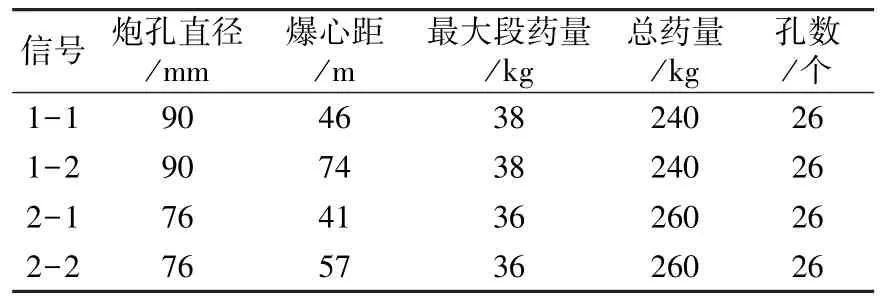
表1 第一組爆破振動信號的條件

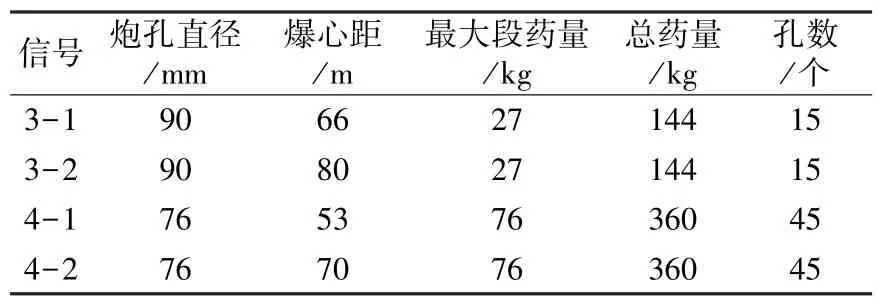
表2 第二組爆破振動信號的條件

對爆破垂直向振動速度信號(1-1，2-1/，3-1/，4-1)進行Fourier分析，可得信號的功率譜密度(PSD)圖，如圖1所示。通過Fourier分析的PSD圖可知，爆破振動信號1-1，2-1，3-1，4-1的主頻分別為48.83，85.94，60.55，107.4 Hz。各測點對應信號的垂直向速度-時程曲線如圖2所示。

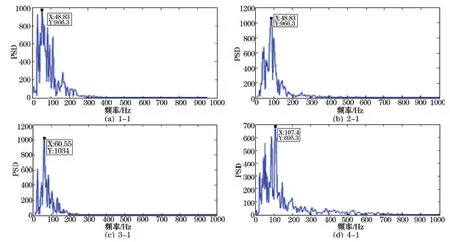
圖1 爆破振動信號(1－1，2－1，3－1，4－1)的功率譜密度

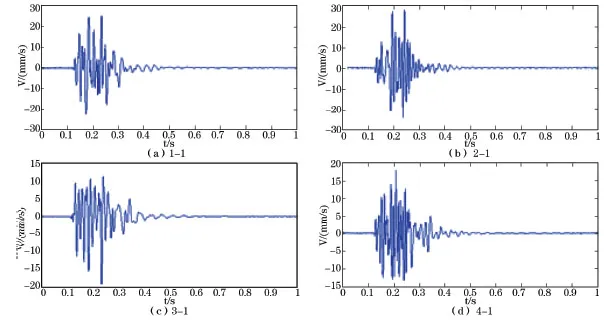
圖2 實測爆破振動信號(1－1，2－1，3－1，4－1)速度時程曲線

2 爆破振動信號的小波分析

2.1 爆破振動信號的小波分解

對爆破振動信號進行小波時頻特性分析時，采用較優小波基[8]sym8對實測爆破地震波進行7層分解，得到8個頻帶的小波分解系數。設置采樣率為2000 Hz，根據香農(Shannon)采樣定理其奈奎斯特(Nyquist)頻率為1000 Hz。由小波分解原理，得

到8個頻帶的分解系數(a7：0～7.8125 Hz、d7：7.8125～15.625 Hz、d6：15.625～31.25 Hz、d5：31.25～62.5 Hz、d4：62.5～125 Hz、d3：125～250 Hz、d2：250～500 Hz、d1：500～1000 Hz)。將各個頻帶的小波分解系數重構后，可得不同頻帶的爆破振動分量的時程曲線。信號1-1的振動分量如圖3～圖10所示。

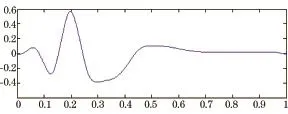
圖3 0～7.815 Hz爆破振動分量

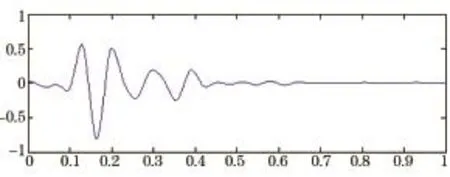
圖4 7.815～15.625 Hz爆破振動分量

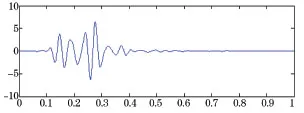
圖5 15.625～31.25 Hz爆破振動分量

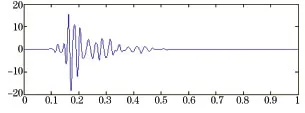
圖6 31.25～62.5 Hz爆破振動分量

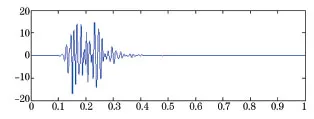
圖7 62.5～125 Hz爆破振動分量

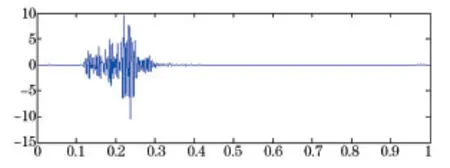
圖8 125～250 Hz爆破振動分量

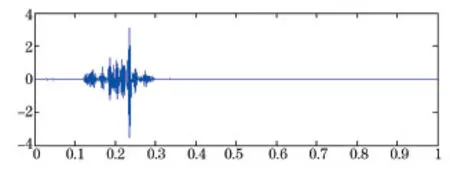
圖9 250～500 Hz爆破振動分量

圖10 500～1000 Hz爆破振動分量

2.2 各頻帶的能量表征

將爆破振動信號s(t)進行層次為N的小波分解重構，對應信號的總能量E為：

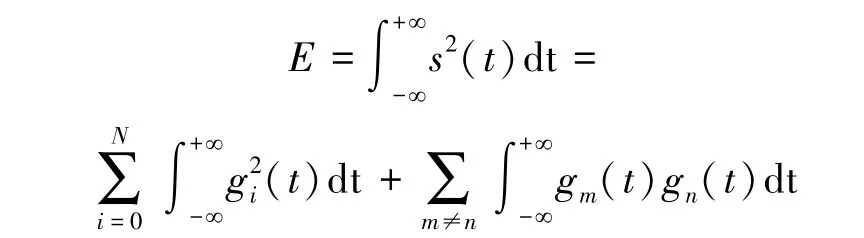
由小波函數的正交性可知，上式第二部分為零，因而可以簡化為：

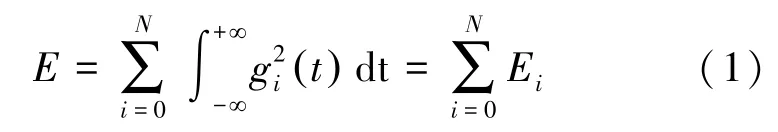
式中，Ei為爆破振動分量的小波頻帶能量；g為爆破振動信號s(t)小波分解的高頻部分，下標對應所分解的層次。

各頻帶爆破振動分量的小波頻帶能量為：

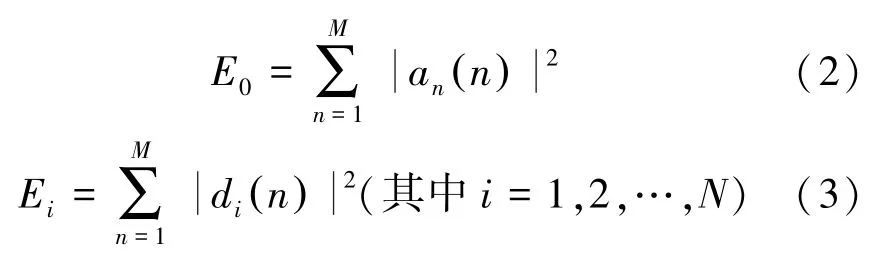
式中，M為采樣點數；aN(n)為爆破振動信號小波分解的逼近系數；di(n)為爆破振動信號小波分解的細節系數。

各頻帶的能量占總能量的比例為：

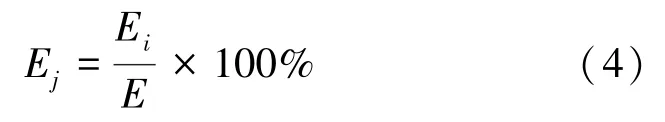
由式(1)、式(2)、式(3)、式(4)可得信號經小波分解后不同頻帶的能量。

3 爆破振動信號頻帶能量分布特征

根據式(1)～(4)使用MATLAB語言編制計算程序，可獲得兩種不同孔徑爆破振動信號的總能量、

各頻帶爆破振動分量的頻帶PPV和小波頻帶能量及其分布。各振動信號的頻帶參數如表3～表10所示。

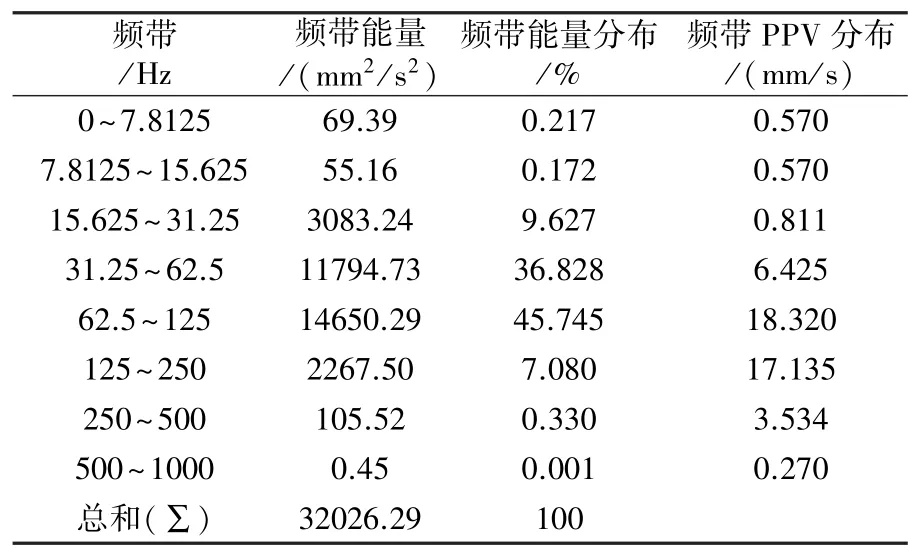
表3 爆破振動信號1－1的頻帶參數

表4 爆破振動信號1－2的頻帶參數

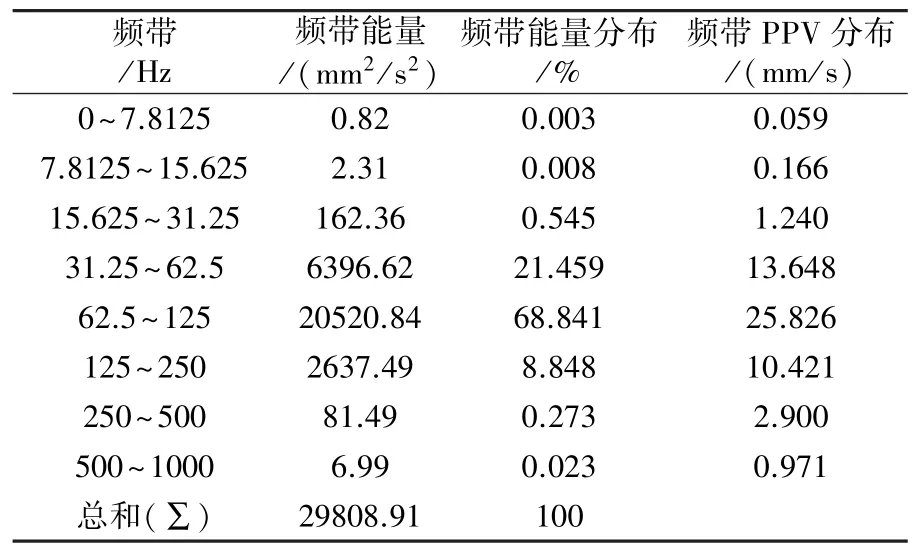
表5 爆破振動信號2－1的頻帶參數

表6 爆破振動信號2－2的頻帶參數

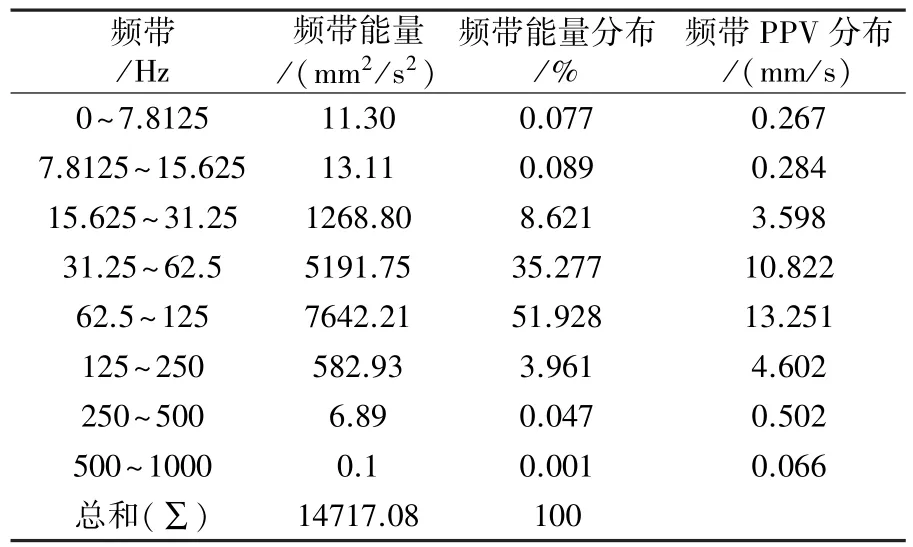
表7 爆破振動信號3－1的頻帶參數

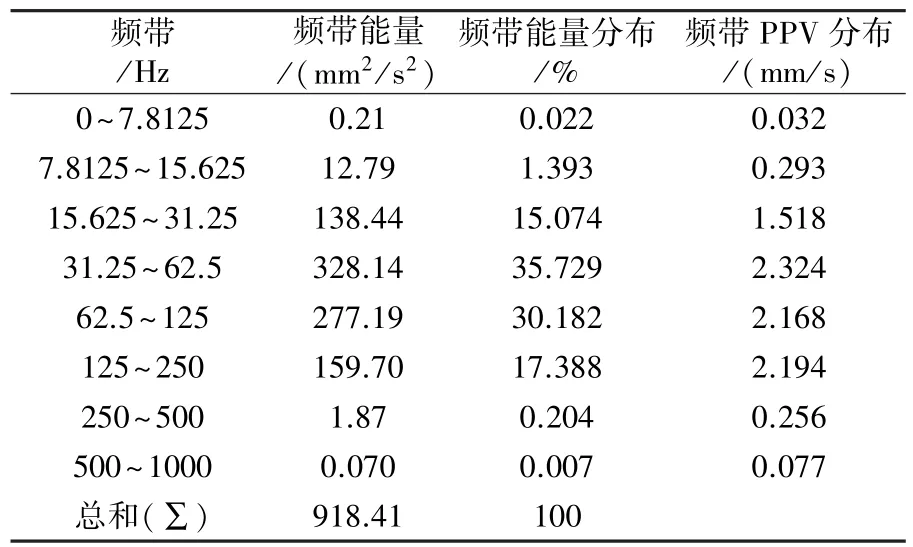
表8 爆破振動信號3－2的頻帶參數

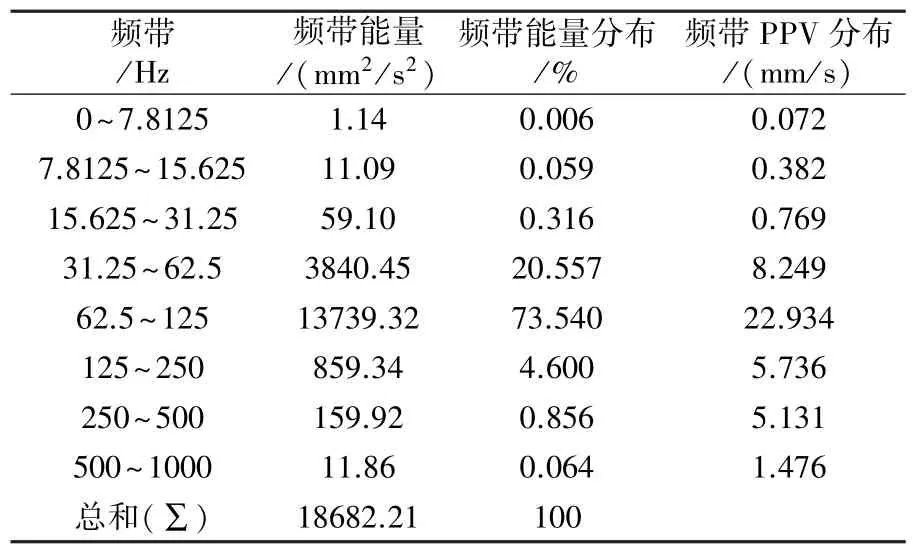
表9 爆破振動信號4－1的頻帶參數

表10 爆破振動信號4－2的頻帶參數

從爆破振動信號的頻帶能量分布可看出，在0～1000 Hz范圍內都有能量分布，能量主要集中在31.25～250 Hz中高頻范圍內，根據Fourier頻譜分析

可知，四段信號的主頻與能量主要分布頻帶一致，而且峰值速度頻帶分布也一致。在31.25 Hz以下，信號1-1，2-1，3-1，4-1的能量占總能量的比例分別為10.016，0.556，8.787，0.381；信號1-2，2-2，3-2，4-2的能量占總能量的比例分別為33.321，2.433，16.511，4.406，低頻成分所占比例較少。可以發現直徑90 mm炮孔在低頻帶能量所占比例高于直徑76 mm炮孔所占比例，而且隨著爆心距的增加，低頻成分都有不同程度的增加趨勢。根據四段信號的主頻可知，孔徑90 mm炮孔的主頻要低于孔徑76 mm炮孔的主頻。表明小孔徑炮孔對降低爆破振動效果要好于大孔徑炮孔。

根據表1、表3和表5可看出，信號2-1(直徑76 mm炮孔)與信號1-1(直徑90 mm炮孔)相比，最大段藥量二者相差不大、總藥量信號 2-1多20 kg、炮孔數量相同；76 mm炮孔爆破振動總能量是90 mm炮孔的93%，即在其它條件相差不大時，小孔徑炮孔的爆破振動能量小。根據表2、表7和表9可看出，信號4-1(直徑76 mm炮孔)與信號3-1(直徑90 mm炮孔)相比，最大段藥量是其2.82倍、總藥量是其2.5倍、孔數是其3倍，76 mm炮孔爆破振動總能量也僅為是90 mm炮孔的127%，相比信號1-1和信號2-1，藥量增加很多，而能量并未呈比例增加，可以說明小孔徑、多孔數的爆破可以降低爆破振動能量。因此，采用小孔徑多數量炮孔布置對降低爆破振動能量有一定效果。

根據圖3～圖10的爆破振動分量以及表1可知，各頻帶能量與峰值速度呈正比，通過不同頻帶振動分量的時程特性得知，在中、低頻帶，信號的持續時間較長，衰減緩慢；在高頻帶，信號的持續時間較短，衰減較快，其能量也少。所以，可以通過小波頻帶能量來反映爆破振動持續時間的影響。

根據表3～表10可得出，在62.5～125 Hz頻帶內，直徑76 mm炮孔所占總能量的比例都要高于直徑90 mm炮孔所占總能量比例。由上述對圖3～圖10的分析可知，在高頻帶信號的衰減較快，也就是說直徑76 mm炮孔的能量衰減要快于直徑90 mm炮孔的能量衰減。這說明大孔徑炮孔的振動衰減比小孔徑炮孔的衰減緩慢，持續時間也比小孔徑炮孔長。

4 結 論

(1)結合Fourier頻譜分析和小波分析，通過Fourier的主頻提取和小波分析的頻帶能量、頻帶PPV提取優勢互補，可更有效的處理和分析爆破振動信號。

(2)不同炮孔直徑的爆破振動信號成分主要分布在31.25～250 Hz中高頻范圍內，小孔徑炮孔的主頻高于大孔徑的主頻。小孔徑炮孔的低頻成分所占比例小于大孔徑炮孔，且隨爆心距增加，兩種孔徑的低頻成分都有增加趨勢。

(3)分析兩種孔徑在62.5～125 Hz頻帶內所占總能量比例，可知大孔徑的爆破振動能量衰減要慢于小孔徑的能量衰減，且持續時間長。

(4)根據不同炮孔直徑、不同最大段藥量、不同總藥量、不同孔數對比，采用小孔徑多數量炮孔布置對降低爆破振動能量有一定效果。

[1] 盧文波，HUSTRULID W.質點峰值振動速度衰減公式的改進[J].工程爆破，2002，8(3)：1-4.

[2] 李洪濤，盧文波，舒大強.爆破地震波的能量衰減規律研究[J].巖石力學與工程學報，2010，29(S1)：3364-3369.

[3] 凌同華，李夕兵.單段爆破振動信號頻帶能量分布特征的小波包分析[J].振動與沖擊，2007，26(5)：41-43.

[4] 凌同華，李夕兵.多段微差爆破振動信號頻帶能量分布特征的小波包分析[J].巖石力學與工程學報，2005，24(7)1117-1122.

[5] 高 山，王茂玲，史太祿.孔徑對爆破質點震動速度衰減的影響[J].采礦技術，2003，3(4)：36-37，40.

[6] 梁 虎，丁松波等.炮孔直徑對爆破振動的影響[J].采礦技術，2014，14(5)：144-147.

[7] 婁建武，龍 源.爆破震動信號的特征提取及識別技術研究[J].振動與沖擊，2003，22(3)：80-84.

[8] 中國生.基于小波變換爆破振動的應用基礎研究[D].長沙：中南大學，2006.

[9] 張德豐.MATLAB小波分析[M].北京：機械工業出版社，2009.

2016-06-25)

徐榮文(1989-)，男，遼寧阜新人，碩士研究生，從事爆破工程與隧道工程研究，Email：435237773＠qq.com。

國家自然科學基金資助項目(51274049).